北京海淀外国语学校2023~2024学年第二学期初三开学考数学试卷(PDF版无答案)
文档属性
| 名称 | 北京海淀外国语学校2023~2024学年第二学期初三开学考数学试卷(PDF版无答案) |  | |
| 格式 | |||
| 文件大小 | 383.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-09 08:43:21 | ||
图片预览

文档简介
初三(下)数学练习题一
班级 姓名
一、填空题(共 8小题,每小题 2分)
1.如图,把一块直角三角板的直角顶点放在直尺的一边上,
若 2 40 ,则 1 ( )
A.60 B.50 C.40 D.30
2.从 1,2,3,4这四个数中一次随机地取两个数,则两数之和大于 4的概率是( )
1 1
A 1 2. 2 B. C. D.3 6 3
3.实数 a,b在数轴上对应的点的位置如图所示,下列结论正确的是( )
A. a b B. a b C. | a | | b | D.a b 0
4.如图,正五边形 ABCDE放入某平面直角坐标系后,若顶点 A,B,C,D的坐标分别是 0,a ,
3, 2 , b,m , b,m ,则点 E的坐标是()
A. 2, 3 B. 2,3 C. 3,2 D. 3, 2
y k5.函数 x 0 的图象如图所示,那么函数 y kx2 k的图象大致是( )
x
A. B. C. D.
6.点 A x1, y1 ,B x2 , y2
1
在反比例函数 y x的图象上,下列推断正确的是( )
A.若 x1 x2,则 y1 y2 B.若 x1 x2,则 y1 y2
C.若 x1 x2 0,则 y1 y2 0 D.存在 x1 x2,使得 y1 y2
9
7.如图,矩形OABC的对角线OB与反比例函数 y x 0 相交于点 D,
x
OD 3
且 ,则矩形OABC的面积为( ).
OB 5
25
A.50 B.25 C.15 D.
2
试卷第 1页,共 8页
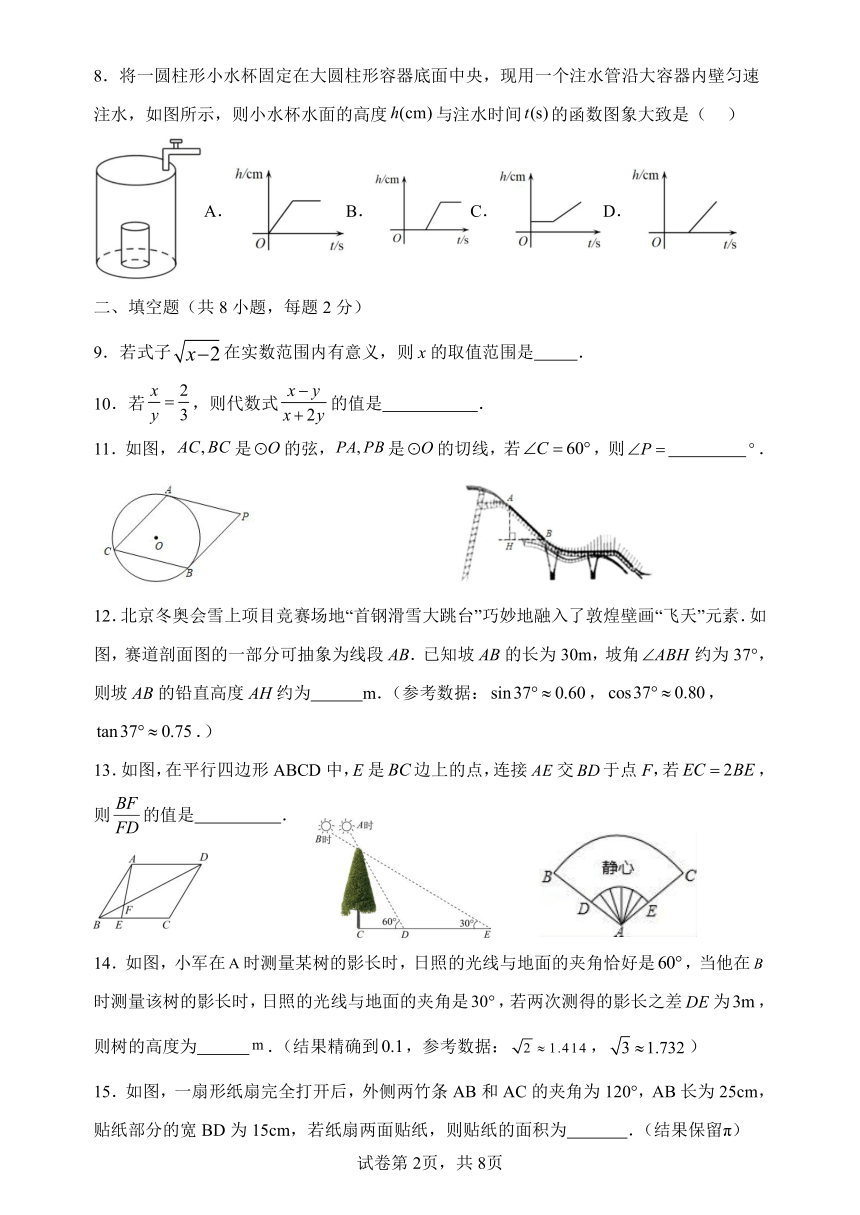
8.将一圆柱形小水杯固定在大圆柱形容器底面中央,现用一个注水管沿大容器内壁匀速
注水,如图所示,则小水杯水面的高度 h(cm)与注水时间 t(s)的函数图象大致是( )
A. B. C. D.
二、填空题(共 8小题,每题 2分)
9.若式子 x 2在实数范围内有意义,则 x的取值范围是 .
x 2 x y
10.若 y 3,则代数式 x 2y 的值是 .
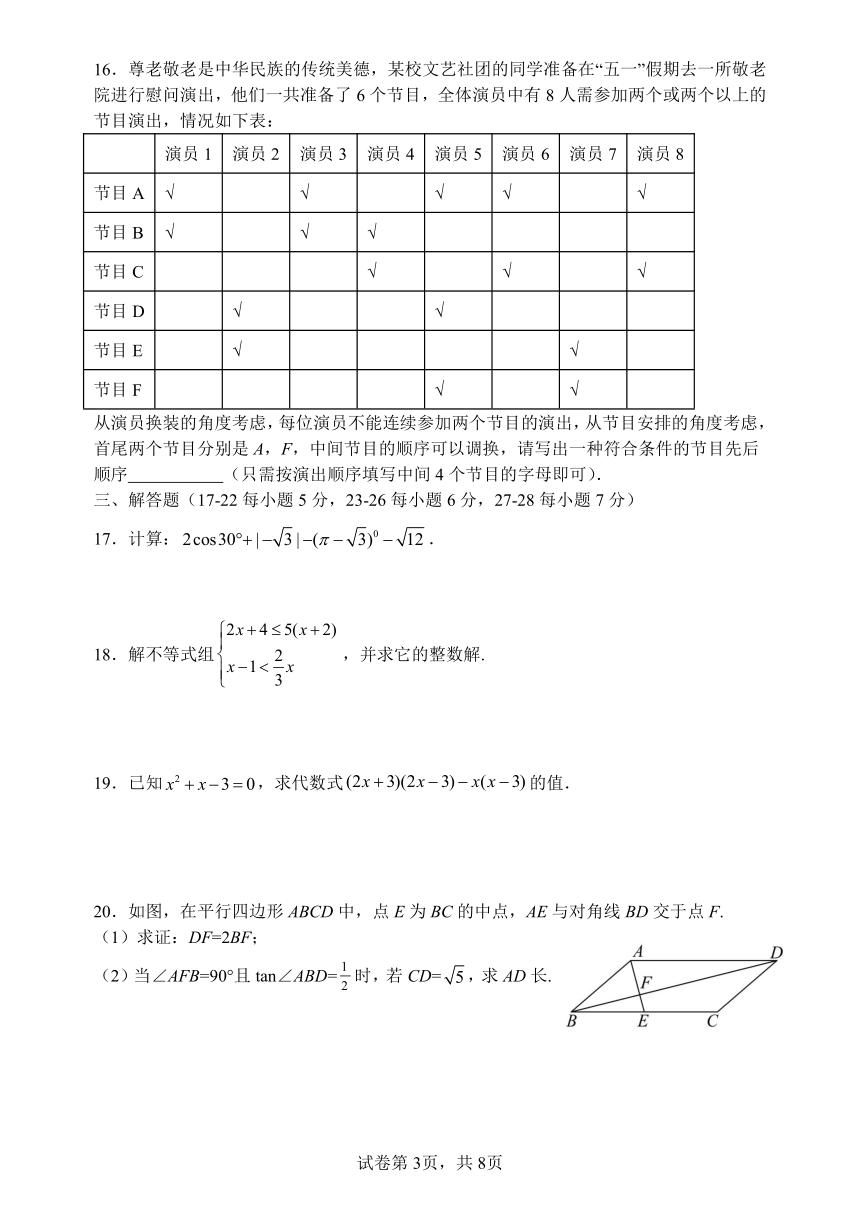
11.如图,AC,BC是 O的弦,PA,PB是 O的切线,若 C 60 ,则 P .
12.北京冬奥会雪上项目竞赛场地“首钢滑雪大跳台”巧妙地融入了敦煌壁画“飞天”元素.如
图,赛道剖面图的一部分可抽象为线段 AB.已知坡 AB的长为 30m,坡角 ABH 约为 37°,
则坡 AB的铅直高度 AH约为 m.(参考数据: sin37 0.60,cos37 0.80,
tan37 0.75.)
13.如图,在平行四边形 ABCD中,E是 BC边上的点,连接 AE交BD于点 F,若 EC 2BE,
BF
则 的值是 .
FD
14.如图,小军在A时测量某树的影长时,日照的光线与地面的夹角恰好是60 ,当他在 B
时测量该树的影长时,日照的光线与地面的夹角是30 ,若两次测得的影长之差DE为3m,
则树的高度为 m.(结果精确到0.1,参考数据: 2 1 .414, 3 1.732)
15.如图,一扇形纸扇完全打开后,外侧两竹条 AB和 AC的夹角为 120°,AB长为 25cm,
贴纸部分的宽 BD为 15cm,若纸扇两面贴纸,则贴纸的面积为 .(结果保留π)
试卷第 2页,共 8页
16.尊老敬老是中华民族的传统美德,某校文艺社团的同学准备在“五一”假期去一所敬老
院进行慰问演出,他们一共准备了 6个节目,全体演员中有 8人需参加两个或两个以上的
节目演出,情况如下表:
演员 1 演员 2 演员 3 演员 4 演员 5 演员 6 演员 7 演员 8
节目 A √ √ √ √ √
节目 B √ √ √
节目 C √ √ √
节目 D √ √
节目 E √ √
节目 F √ √
从演员换装的角度考虑,每位演员不能连续参加两个节目的演出,从节目安排的角度考虑,
首尾两个节目分别是 A,F,中间节目的顺序可以调换,请写出一种符合条件的节目先后
顺序 (只需按演出顺序填写中间 4个节目的字母即可).
三、解答题(17-22每小题 5分,23-26每小题 6分,27-28每小题 7分)
17.计算:2cos30 | 3 | ( 3)0 12.
2x 4 5(x 2)
18.解不等式组 ,并求它的整数解.
x
2
1 x
3
19.已知 x2 x 3 0,求代数式 (2x 3)(2x 3) x(x 3)的值.
20.如图,在平行四边形 ABCD中,点 E为 BC的中点,AE与对角线 BD交于点 F.
(1)求证:DF=2BF;
(2)当∠AFB=90° 1且 tan∠ABD= 2 时,若 CD= 5,求 AD长.
试卷第 3页,共 8页
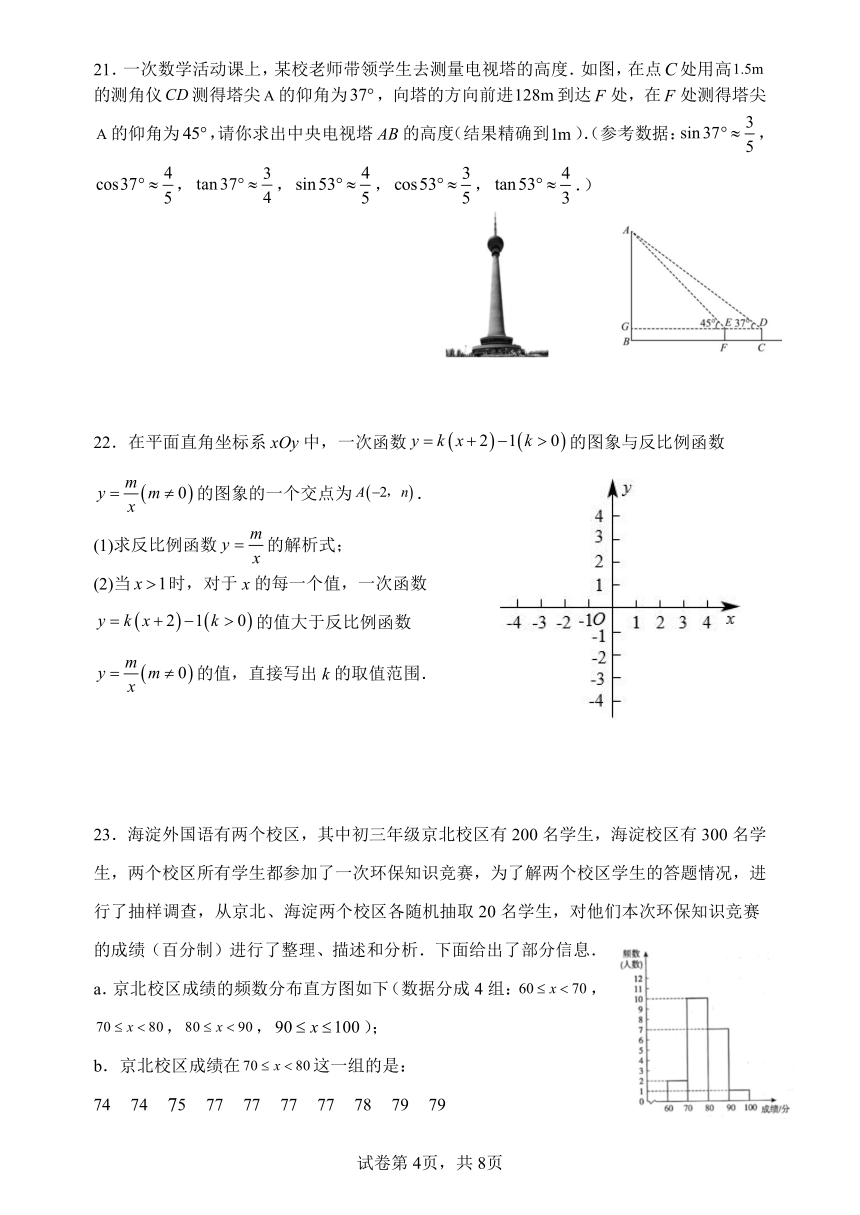
21.一次数学活动课上,某校老师带领学生去测量电视塔的高度.如图,在点C处用高1.5m
的测角仪CD测得塔尖A的仰角为37 ,向塔的方向前进128m到达 F 处,在 F 处测得塔尖
3
A的仰角为 45 ,请你求出中央电视塔 AB的高度(结果精确到1m)(.参考数据:sin 37 ,
5
cos37 4 , tan 37
3
, sin53
4 3 4
, cos53 , tan53 .)
5 4 5 5 3
22.在平面直角坐标系 xOy中,一次函数 y k x 2 1 k 0 的图象与反比例函数
y m m 0 的图象的一个交点为 A 2,n .
x
m
(1)求反比例函数 y 的解析式;
x
(2)当 x 1时,对于 x的每一个值,一次函数
y k x 2 1 k 0 的值大于反比例函数
y m m 0 的值,直接写出 k的取值范围.
x
23.海淀外国语有两个校区,其中初三年级京北校区有 200名学生,海淀校区有 300名学
生,两个校区所有学生都参加了一次环保知识竞赛,为了解两个校区学生的答题情况,进
行了抽样调查,从京北、海淀两个校区各随机抽取 20名学生,对他们本次环保知识竞赛
的成绩(百分制)进行了整理、描述和分析.下面给出了部分信息.
a.京北校区成绩的频数分布直方图如下(数据分成 4组:60 x 70,
70 x 80,80 x 90,90 x 100);
b.京北校区成绩在 70 x 80这一组的是:
74 74 75 77 77 77 77 78 79 79
试卷第 4页,共 8页
c.京北、海淀两校区成绩的平均数、中位数如下:
平均数 中位数
京北校区 79.5 m
海淀校区 77 81.5
根据以上信息,回答下列问题:
(1)写出表中 m的值;
(2)两个校区分别对本次抽取的学生的成绩进行等级赋分,超过本校区的平均分就可以赋予
等级 A,判断在本次抽取的学生中哪个校区赋予等级 A的学生更多,并说明理由;
(3)估计该校初三年级所有学生本次环保知识竞赛的平均分为 (直接写出结果).
24.如图是某小型跳台滑雪训练场的横截面示意图,取某一位置的水平线为 x轴,过跳台
1
A 2
4 4
终点 作水平线的垂线为 y轴,建立平面直角坐标系,图中的抛物线C1 : y x x 12 3 3
近似表示滑雪场地上的一座小山坡,某滑雪爱好者小张从点 O正上方 A点滑出,滑出后沿
1 2
一段抛物线C2 : y x bx c 运动.8
(1)当小张滑到离 A处的水平距离为 6米时,其滑行高度
17
最大,为 米,则b ________.
2
(2)在(1)的条件下,当小张滑出后离 A的水平距离为多
4
少米时,他滑行高度与小山坡的竖直距离为 米?
3
(3)小张若想滑行到最大高度时恰好在坡顶正上方,且与
坡顶距离不低于 3米,求跳台滑出点的最小高度.
试卷第 5页,共 8页
25.如图, O是 ABC的外接圆,AB是直径,OD OC,且 ADO BOC .
(1)求证: AD是 O的切线;
1
(2)若 tan BAC , AD 3,求 O的半径.2
26.已知抛物线 y ax2 bx 4的对称轴为直线 x t.
(1)若点 (2, 4)在抛物线上,求 t的值;
(2)若点 (x1,3), (x2 ,6)在抛物线上,
①当 t 1时,求 a的取值范围;
②若 t x1 x2,且 x2 x1 1,直接写出 a的取值范围.
试卷第 6页,共 8页
27.在 ABC中, ACB 90 ,CA CB,点D为射线CA上一点,过点D作DE∥CB且
DE CB(点 E在点D的右侧),射线 ED交射线 BA于点 F ,点H是 AF的中点,连接HC,
HE.
(1)如图1,当点D在线段CA上时,判断线段
HE与HC的数量关系及位置关系;
(2)当点D在线段CA的延长线上时,依题意
补全图 2.用等式表示线段CB,CD,CH 之
间的数量关系,并证明.
试卷第 7页,共 8页
28.在平面直角坐标系 xOy中,已知点M (a,b),N .对于点 P给出如下定义:将点 P向右
(a 0)或向左 (a 0)平移 a 个单位长度,再向上 (b 0)或向下 (b 0)平移 b个单位长度,
得到点P',点P'关于点 N的对称点为Q,称点Q为点 P的“对应点”.
(1)如图,点M (1,1),点N在线段OM 的延长线上,若点 P( 2,0),点Q为点 P的“对应点”.
①在图中画出点Q;
1
②连接 PQ,交线段ON于点T.求证: NT OM;
2
1
(2) O的半径为 1,M 是 O上一点,点N在线段OM 上,且ON t ( t 1) ,若 P为 O
2
外一点,点Q为点 P的“对应点”,连接 PQ.当点M 在 O上运动时直接写出 PQ长的最大值
与最小值的差(用含 t的式子表示).
试卷第 8页,共 8页
班级 姓名
一、填空题(共 8小题,每小题 2分)
1.如图,把一块直角三角板的直角顶点放在直尺的一边上,
若 2 40 ,则 1 ( )
A.60 B.50 C.40 D.30
2.从 1,2,3,4这四个数中一次随机地取两个数,则两数之和大于 4的概率是( )
1 1
A 1 2. 2 B. C. D.3 6 3
3.实数 a,b在数轴上对应的点的位置如图所示,下列结论正确的是( )
A. a b B. a b C. | a | | b | D.a b 0
4.如图,正五边形 ABCDE放入某平面直角坐标系后,若顶点 A,B,C,D的坐标分别是 0,a ,
3, 2 , b,m , b,m ,则点 E的坐标是()
A. 2, 3 B. 2,3 C. 3,2 D. 3, 2
y k5.函数 x 0 的图象如图所示,那么函数 y kx2 k的图象大致是( )
x
A. B. C. D.
6.点 A x1, y1 ,B x2 , y2
1
在反比例函数 y x的图象上,下列推断正确的是( )
A.若 x1 x2,则 y1 y2 B.若 x1 x2,则 y1 y2
C.若 x1 x2 0,则 y1 y2 0 D.存在 x1 x2,使得 y1 y2
9
7.如图,矩形OABC的对角线OB与反比例函数 y x 0 相交于点 D,
x
OD 3
且 ,则矩形OABC的面积为( ).
OB 5
25
A.50 B.25 C.15 D.
2
试卷第 1页,共 8页
8.将一圆柱形小水杯固定在大圆柱形容器底面中央,现用一个注水管沿大容器内壁匀速
注水,如图所示,则小水杯水面的高度 h(cm)与注水时间 t(s)的函数图象大致是( )
A. B. C. D.
二、填空题(共 8小题,每题 2分)
9.若式子 x 2在实数范围内有意义,则 x的取值范围是 .
x 2 x y
10.若 y 3,则代数式 x 2y 的值是 .
11.如图,AC,BC是 O的弦,PA,PB是 O的切线,若 C 60 ,则 P .
12.北京冬奥会雪上项目竞赛场地“首钢滑雪大跳台”巧妙地融入了敦煌壁画“飞天”元素.如
图,赛道剖面图的一部分可抽象为线段 AB.已知坡 AB的长为 30m,坡角 ABH 约为 37°,
则坡 AB的铅直高度 AH约为 m.(参考数据: sin37 0.60,cos37 0.80,
tan37 0.75.)
13.如图,在平行四边形 ABCD中,E是 BC边上的点,连接 AE交BD于点 F,若 EC 2BE,
BF
则 的值是 .
FD
14.如图,小军在A时测量某树的影长时,日照的光线与地面的夹角恰好是60 ,当他在 B
时测量该树的影长时,日照的光线与地面的夹角是30 ,若两次测得的影长之差DE为3m,
则树的高度为 m.(结果精确到0.1,参考数据: 2 1 .414, 3 1.732)
15.如图,一扇形纸扇完全打开后,外侧两竹条 AB和 AC的夹角为 120°,AB长为 25cm,
贴纸部分的宽 BD为 15cm,若纸扇两面贴纸,则贴纸的面积为 .(结果保留π)
试卷第 2页,共 8页
16.尊老敬老是中华民族的传统美德,某校文艺社团的同学准备在“五一”假期去一所敬老
院进行慰问演出,他们一共准备了 6个节目,全体演员中有 8人需参加两个或两个以上的
节目演出,情况如下表:
演员 1 演员 2 演员 3 演员 4 演员 5 演员 6 演员 7 演员 8
节目 A √ √ √ √ √
节目 B √ √ √
节目 C √ √ √
节目 D √ √
节目 E √ √
节目 F √ √
从演员换装的角度考虑,每位演员不能连续参加两个节目的演出,从节目安排的角度考虑,
首尾两个节目分别是 A,F,中间节目的顺序可以调换,请写出一种符合条件的节目先后
顺序 (只需按演出顺序填写中间 4个节目的字母即可).
三、解答题(17-22每小题 5分,23-26每小题 6分,27-28每小题 7分)
17.计算:2cos30 | 3 | ( 3)0 12.
2x 4 5(x 2)
18.解不等式组 ,并求它的整数解.
x
2
1 x
3
19.已知 x2 x 3 0,求代数式 (2x 3)(2x 3) x(x 3)的值.
20.如图,在平行四边形 ABCD中,点 E为 BC的中点,AE与对角线 BD交于点 F.
(1)求证:DF=2BF;
(2)当∠AFB=90° 1且 tan∠ABD= 2 时,若 CD= 5,求 AD长.
试卷第 3页,共 8页
21.一次数学活动课上,某校老师带领学生去测量电视塔的高度.如图,在点C处用高1.5m
的测角仪CD测得塔尖A的仰角为37 ,向塔的方向前进128m到达 F 处,在 F 处测得塔尖
3
A的仰角为 45 ,请你求出中央电视塔 AB的高度(结果精确到1m)(.参考数据:sin 37 ,
5
cos37 4 , tan 37
3
, sin53
4 3 4
, cos53 , tan53 .)
5 4 5 5 3
22.在平面直角坐标系 xOy中,一次函数 y k x 2 1 k 0 的图象与反比例函数
y m m 0 的图象的一个交点为 A 2,n .
x
m
(1)求反比例函数 y 的解析式;
x
(2)当 x 1时,对于 x的每一个值,一次函数
y k x 2 1 k 0 的值大于反比例函数
y m m 0 的值,直接写出 k的取值范围.
x
23.海淀外国语有两个校区,其中初三年级京北校区有 200名学生,海淀校区有 300名学
生,两个校区所有学生都参加了一次环保知识竞赛,为了解两个校区学生的答题情况,进
行了抽样调查,从京北、海淀两个校区各随机抽取 20名学生,对他们本次环保知识竞赛
的成绩(百分制)进行了整理、描述和分析.下面给出了部分信息.
a.京北校区成绩的频数分布直方图如下(数据分成 4组:60 x 70,
70 x 80,80 x 90,90 x 100);
b.京北校区成绩在 70 x 80这一组的是:
74 74 75 77 77 77 77 78 79 79
试卷第 4页,共 8页
c.京北、海淀两校区成绩的平均数、中位数如下:
平均数 中位数
京北校区 79.5 m
海淀校区 77 81.5
根据以上信息,回答下列问题:
(1)写出表中 m的值;
(2)两个校区分别对本次抽取的学生的成绩进行等级赋分,超过本校区的平均分就可以赋予
等级 A,判断在本次抽取的学生中哪个校区赋予等级 A的学生更多,并说明理由;
(3)估计该校初三年级所有学生本次环保知识竞赛的平均分为 (直接写出结果).
24.如图是某小型跳台滑雪训练场的横截面示意图,取某一位置的水平线为 x轴,过跳台
1
A 2
4 4
终点 作水平线的垂线为 y轴,建立平面直角坐标系,图中的抛物线C1 : y x x 12 3 3
近似表示滑雪场地上的一座小山坡,某滑雪爱好者小张从点 O正上方 A点滑出,滑出后沿
1 2
一段抛物线C2 : y x bx c 运动.8
(1)当小张滑到离 A处的水平距离为 6米时,其滑行高度
17
最大,为 米,则b ________.
2
(2)在(1)的条件下,当小张滑出后离 A的水平距离为多
4
少米时,他滑行高度与小山坡的竖直距离为 米?
3
(3)小张若想滑行到最大高度时恰好在坡顶正上方,且与
坡顶距离不低于 3米,求跳台滑出点的最小高度.
试卷第 5页,共 8页
25.如图, O是 ABC的外接圆,AB是直径,OD OC,且 ADO BOC .
(1)求证: AD是 O的切线;
1
(2)若 tan BAC , AD 3,求 O的半径.2
26.已知抛物线 y ax2 bx 4的对称轴为直线 x t.
(1)若点 (2, 4)在抛物线上,求 t的值;
(2)若点 (x1,3), (x2 ,6)在抛物线上,
①当 t 1时,求 a的取值范围;
②若 t x1 x2,且 x2 x1 1,直接写出 a的取值范围.
试卷第 6页,共 8页
27.在 ABC中, ACB 90 ,CA CB,点D为射线CA上一点,过点D作DE∥CB且
DE CB(点 E在点D的右侧),射线 ED交射线 BA于点 F ,点H是 AF的中点,连接HC,
HE.
(1)如图1,当点D在线段CA上时,判断线段
HE与HC的数量关系及位置关系;
(2)当点D在线段CA的延长线上时,依题意
补全图 2.用等式表示线段CB,CD,CH 之
间的数量关系,并证明.
试卷第 7页,共 8页
28.在平面直角坐标系 xOy中,已知点M (a,b),N .对于点 P给出如下定义:将点 P向右
(a 0)或向左 (a 0)平移 a 个单位长度,再向上 (b 0)或向下 (b 0)平移 b个单位长度,
得到点P',点P'关于点 N的对称点为Q,称点Q为点 P的“对应点”.
(1)如图,点M (1,1),点N在线段OM 的延长线上,若点 P( 2,0),点Q为点 P的“对应点”.
①在图中画出点Q;
1
②连接 PQ,交线段ON于点T.求证: NT OM;
2
1
(2) O的半径为 1,M 是 O上一点,点N在线段OM 上,且ON t ( t 1) ,若 P为 O
2
外一点,点Q为点 P的“对应点”,连接 PQ.当点M 在 O上运动时直接写出 PQ长的最大值
与最小值的差(用含 t的式子表示).
试卷第 8页,共 8页
同课章节目录
