2015人教版数学九上22.2二次函数与一元二次方程PPT课件(共11张PPT)
文档属性
| 名称 | 2015人教版数学九上22.2二次函数与一元二次方程PPT课件(共11张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 188.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-31 17:55:03 | ||
图片预览




文档简介
课件11张PPT。九年级 上册22.2 二次函数与一元二次方程二次函数与一元二次方程的联系再次展示了函数与方
程的联系,一方面可以深化对一元二次方程的认识,
另一方面又可以运用二次函数解决一元二次方程的有
关问题.课件说明学习目标:
了解二次函数与一元二次方程的联系.
学习重点: 二次函数与一元二次方程的联系.课件说明 问题1 以 40 m/s 的速度将小球沿与地面成 30°角的方向 击出时,小球的飞行路线将是一条抛物线.如果不考虑 空气阻力,小球的飞行高度 h (单位:m )与飞行时间 t(单位:s)之间具有函数关系 h = 20t - 5t 2.
(1)小球的飞行高度能否达到 15 m? 如果能,需 要多少飞行时间? (2)小球的飞行高度能否达到 20 m? 如能,需要 多少飞行时间?
(3)小球的飞行高度能否达到 20.5 m? 为什么?
(4)小球从飞出到落地要用多少时间?1.复习知识,回顾方法2.小组合作,类比探究 问题2
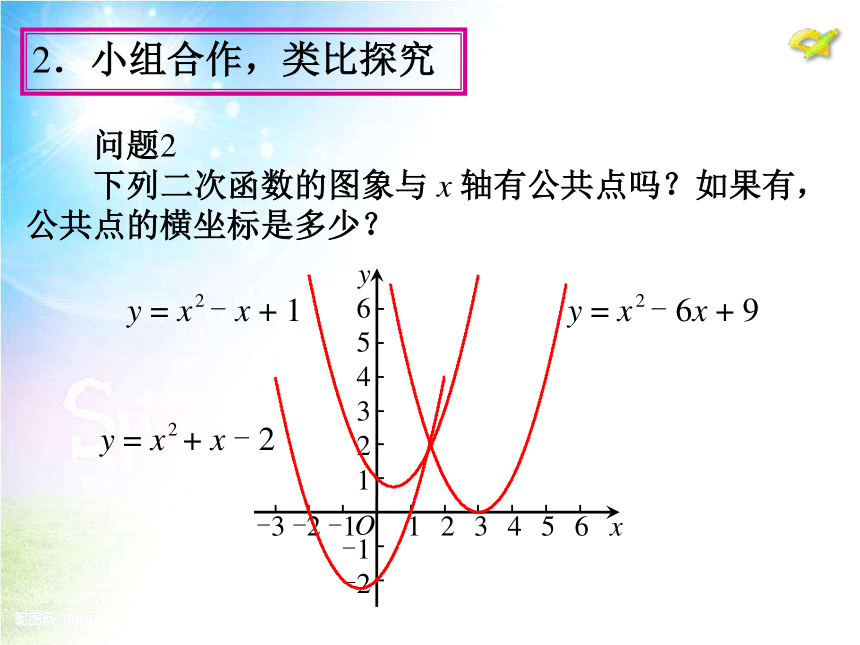
下列二次函数的图象与 x 轴有公共点吗?如果有, 公共点的横坐标是多少? 2.小组合作,类比探究 问题3
当 x 取公共点的横坐标时,函数值是多少? 2.小组合作,类比探究 问题4
由二次函数的图象,你能得出相应的一元二次方程的根吗?二次函数与一元二次方程具有怎样的联系? x 2 + x - 2 = 0
x 2 - 6x + 9 = 0
x 2 - x + 1 = 0 归纳
一般地,从二次函数 y = ax 2 + bx + c 的图象可知:
(1)如果抛物线 y = ax 2 + bx + c 与 x 轴有公共点, 公共点的横坐标是 x0,那么当 x = x0 时,函数值是 0, 因此 x = x0 是方程 ax 2 + bx + c = 0 的一个根.
(2)二次函数 y = ax 2 + bx + c 的图象与 x 轴的位置 关系有三种:没有公共点,有一个公共点,有两个公共 点. 这对应着一元二次方程 ax 2 + bx + c = 0 的根的三种 情况:没有实数根,有两个相等的实数根,有两个不等 的实数根.2.小组合作,类比探究3.运用性质,巩固练习 例 利用函数图象求方程 x 2 - 2x - 2 = 0 的实数根 (结果保留小数点后一位). (1)本节课学了哪些主要内容?
(2)二次函数与一元二次方程有什么区别与联系?4.小结知识,梳理方法 教科书习题 22.2 第 1,3,5 题.5.课后反思,布置作业
学习重点: 二次函数与一元二次方程的联系.课件说明 问题1 以 40 m/s 的速度将小球沿与地面成 30°角的方向 击出时,小球的飞行路线将是一条抛物线.如果不考虑 空气阻力,小球的飞行高度 h (单位:m )与飞行时间 t(单位:s)之间具有函数关系 h = 20t - 5t 2.
(1)小球的飞行高度能否达到 15 m? 如果能,需 要多少飞行时间? (2)小球的飞行高度能否达到 20 m? 如能,需要 多少飞行时间?
(3)小球的飞行高度能否达到 20.5 m? 为什么?
(4)小球从飞出到落地要用多少时间?1.复习知识,回顾方法2.小组合作,类比探究 问题2
下列二次函数的图象与 x 轴有公共点吗?如果有, 公共点的横坐标是多少? 2.小组合作,类比探究 问题3
当 x 取公共点的横坐标时,函数值是多少? 2.小组合作,类比探究 问题4
由二次函数的图象,你能得出相应的一元二次方程的根吗?二次函数与一元二次方程具有怎样的联系? x 2 + x - 2 = 0
x 2 - 6x + 9 = 0
x 2 - x + 1 = 0 归纳
一般地,从二次函数 y = ax 2 + bx + c 的图象可知:
(1)如果抛物线 y = ax 2 + bx + c 与 x 轴有公共点, 公共点的横坐标是 x0,那么当 x = x0 时,函数值是 0, 因此 x = x0 是方程 ax 2 + bx + c = 0 的一个根.
(2)二次函数 y = ax 2 + bx + c 的图象与 x 轴的位置 关系有三种:没有公共点,有一个公共点,有两个公共 点. 这对应着一元二次方程 ax 2 + bx + c = 0 的根的三种 情况:没有实数根,有两个相等的实数根,有两个不等 的实数根.2.小组合作,类比探究3.运用性质,巩固练习 例 利用函数图象求方程 x 2 - 2x - 2 = 0 的实数根 (结果保留小数点后一位). (1)本节课学了哪些主要内容?
(2)二次函数与一元二次方程有什么区别与联系?4.小结知识,梳理方法 教科书习题 22.2 第 1,3,5 题.5.课后反思,布置作业
同课章节目录
