9.4矩形、菱形、正方形(菱形讲义)(无答案)苏科版数学八年级下册
文档属性
| 名称 | 9.4矩形、菱形、正方形(菱形讲义)(无答案)苏科版数学八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 485.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-09 00:00:00 | ||
图片预览



文档简介
9.4矩形、菱形、正方形
(菱形讲义)
教学目的: 1.掌握菱形的性质; 2.掌握菱形的判定证明;
教学重难点: 1.掌握菱形的性质; 2.掌握菱形的判定证明;
知识梳理
【知识点一】菱形的性质 菱形的定义:有一组邻边相等的平行四边形叫做菱形。 菱形的性质: (1)具有平行四边形的所有性质; (2)四条边都相等; (3)两条对角线互相垂直,且每条对角线平分一组对角。 (4)菱形既是中心对称图形又是轴对称图形,菱形的对称中心是菱形对角线的交点,菱形的对称轴是菱形对角线所在的直线,菱形的对称轴过菱形的对称中心。 菱形的面积公式:菱形ABCD的对角线是AC、BD,则菱形的面积公式是:S=底×高,S= 【知识点二】菱形的判定 (
A
)(1)对角线互相垂直的平行四边形是菱形。 (2)四条边相等的四边形是菱形。 (3)一组邻边相等的平行四边形是菱形。
典型例题
【例1】在菱形中,若,则是( ) A.60 B.20 C.80 D.100 【例2】下列说法中正确的是( ) 有一组对边平行的四边形是平行四边形 B.对角线互相垂直的四边形是菱形 C.有一组邻边相等的平行四边形是菱形 D.对角线互相垂直平分的四边形是矩形 【例3】如图,O为矩形ABCD对角线的交点,DEAC,CEBD. (1)试判断四边形OCED的形状,并说明理由; (2)若AB=6,BC=8,求四边形OCED的面积. 【例4】在矩形纸片中,,.将矩形纸片折叠,使点与点重合. (1)连接,求证:四边形是菱形; (2)求折痕的长.
举一反三
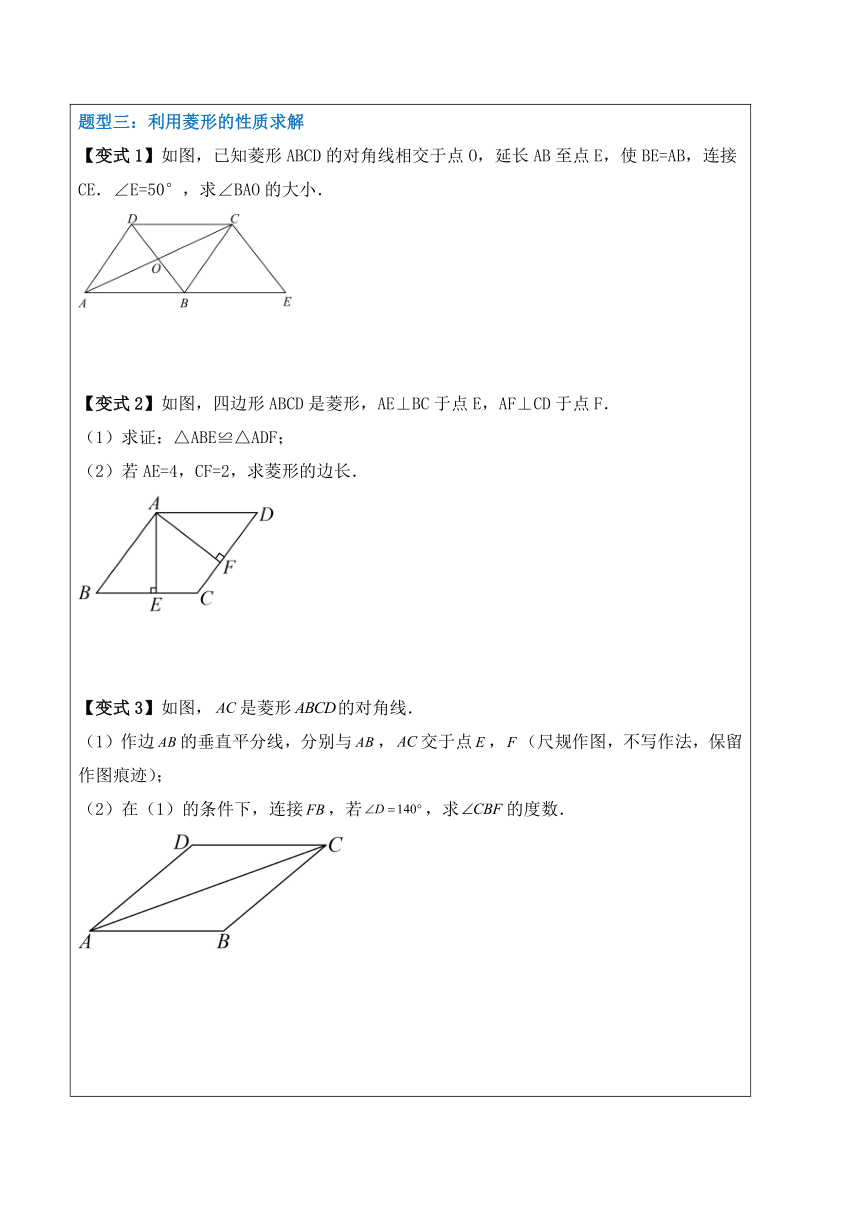
题型一:菱形的性质 【变式1】在菱形中,,连接,则的度数为( ) A. B. C. D. 【变式2】菱形的两条对角线的长分别是6和8 ,则这个菱形的周长是( ) A.24 B.20 C.10 D.5 【变式3】如图,在菱形中,,,则菱形的面积为( ) A.20 B.24 C.30 D.48 题型二:菱形的判定 【变式1】的对角线与相交于点,添加以下条件,不能判定平行四边形为菱形的是( ) A. B. C. D. 【变式2】如图,四边形中,,,,分别是边、、、的中点.若四边形为菱形,则对角线、应满足条件______. 【变式3】如图,在中,点是的中点,点、分别在线段及其延长线上,且,给出下列条件:①;②;③:从中选择一个条件使四边形是菱形,你认为这个条件是_______(只填写序号). 题型三:利用菱形的性质求解 【变式1】如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE.∠E=50°,求∠BAO的大小. 【变式2】如图,四边形ABCD是菱形,AE⊥BC于点E,AF⊥CD于点F. (1)求证:△ABE≌△ADF; (2)若AE=4,CF=2,求菱形的边长. 【变式3】如图,是菱形的对角线. (1)作边的垂直平分线,分别与,交于点,(尺规作图,不写作法,保留作图痕迹); (2)在(1)的条件下,连接,若,求的度数. 题型四:菱形的判定证明 【变式1】如图,点,分别在的边,上,,连接,.请从以下三个条件:①;②;③中,选择一个合适的作为已知条件,使为菱形. (1)你添加的条件是______(填序号); (2)添加了条件后,请证明为菱形. 【变式2】如图,已知四边形是平行四边形,其对角线相交于点O,. (1)是直角三角形吗?请说明理由; (2)求证:四边形是菱形. 【变式3】如图,四边形是平行四边形,,且分别交对角线于点M,N,连接. (1)求证:; (2)若.求证:四边形是菱形.
小试牛刀
一、选择题(共5题) 1.矩形具有而菱形不一定具有的性质是( ) A.邻边相等 B.对角线相等 C.对角线互相平分 D.对角线互相垂直 2.下列命题中,是真命题的是( ) A.平行四边形是轴对称图形 B.对角线互相垂直的四边形是菱形 C.到一条线段两个端点距离相等的点,在这条线段的垂直平分线上 D.在中,若,则是直角三角形 3.如图,在菱形ABCD中,对角线AC,BD相交于点O,下列结论中错误的是( ) A.AB=AD B.AC⊥BD C.AC=BD D.∠DAC=∠BAC 4.如图,在平面直角坐标系中,菱形的顶点D在x轴上,边在y轴上,若点A的坐标为,则C点的坐标为( ) A. B. C. D. 5.如图,菱形的对边、上分别有两个动点M和N,若的最大值为,最小值为4,则菱形的面积为( ) A.18 B.28 C. D. 二、填空题(共5题) 6.点是菱形的对称中心,,连接,则的度数为 . 7.如图,菱形的对角线,相交于点,点是边的中点,若,则的长为 . 8.如图,在平面直角坐标系中,菱形的顶点在轴的正半轴上,点的坐标为,则点的坐标为 . 9.如图,菱形的边长为2,,对角线与交于点,为中点,为中点,连接,则的长为 . 10.如图,在菱形中,.若M、N分别是边上的动点,且,作,垂足分别为E、F,则的值为 . 三、解答题(共5题) 11.已知. (1)化简; (2)若,是菱形两条对角线的长,且该菱形的面积为,求的值. 12.如图,在四边形中,,,对角线交于点,平分,过点作交的延长线于点,连接. (1) 求证:四边形是菱形; (2) 若,,求的长. 13.如图,四边形是平行四边形,连接,交于点,平分交于点,平分交于点,连接,. (1)求证:; (2)若四边形是菱形且,,求四边形的面积. 14.如图,在矩形中,. 在图①中,P是上一点,垂直平分,分别交边于点E、F,求证:四边形是菱形; 若菱形的四个顶点都在矩形的边上,当菱形的面积最大时,菱形的边长是 . 15.综合与实践 问题情境:如图1,在中,,点D是的中点,连接,将沿直线折叠,点B落在点E处,连接. 独立思考: 在图1中,若,,则的长为______; 实践探究: 在图1中,请你判断与的位置关系,并说明理由; 问题解决: 如图2,在中,,,点D是的中点,连接,将沿直线折叠,点B落在点E处,连接.请判断四边形的形状,并说明理由.
(菱形讲义)
教学目的: 1.掌握菱形的性质; 2.掌握菱形的判定证明;
教学重难点: 1.掌握菱形的性质; 2.掌握菱形的判定证明;
知识梳理
【知识点一】菱形的性质 菱形的定义:有一组邻边相等的平行四边形叫做菱形。 菱形的性质: (1)具有平行四边形的所有性质; (2)四条边都相等; (3)两条对角线互相垂直,且每条对角线平分一组对角。 (4)菱形既是中心对称图形又是轴对称图形,菱形的对称中心是菱形对角线的交点,菱形的对称轴是菱形对角线所在的直线,菱形的对称轴过菱形的对称中心。 菱形的面积公式:菱形ABCD的对角线是AC、BD,则菱形的面积公式是:S=底×高,S= 【知识点二】菱形的判定 (
A
)(1)对角线互相垂直的平行四边形是菱形。 (2)四条边相等的四边形是菱形。 (3)一组邻边相等的平行四边形是菱形。
典型例题
【例1】在菱形中,若,则是( ) A.60 B.20 C.80 D.100 【例2】下列说法中正确的是( ) 有一组对边平行的四边形是平行四边形 B.对角线互相垂直的四边形是菱形 C.有一组邻边相等的平行四边形是菱形 D.对角线互相垂直平分的四边形是矩形 【例3】如图,O为矩形ABCD对角线的交点,DEAC,CEBD. (1)试判断四边形OCED的形状,并说明理由; (2)若AB=6,BC=8,求四边形OCED的面积. 【例4】在矩形纸片中,,.将矩形纸片折叠,使点与点重合. (1)连接,求证:四边形是菱形; (2)求折痕的长.
举一反三
题型一:菱形的性质 【变式1】在菱形中,,连接,则的度数为( ) A. B. C. D. 【变式2】菱形的两条对角线的长分别是6和8 ,则这个菱形的周长是( ) A.24 B.20 C.10 D.5 【变式3】如图,在菱形中,,,则菱形的面积为( ) A.20 B.24 C.30 D.48 题型二:菱形的判定 【变式1】的对角线与相交于点,添加以下条件,不能判定平行四边形为菱形的是( ) A. B. C. D. 【变式2】如图,四边形中,,,,分别是边、、、的中点.若四边形为菱形,则对角线、应满足条件______. 【变式3】如图,在中,点是的中点,点、分别在线段及其延长线上,且,给出下列条件:①;②;③:从中选择一个条件使四边形是菱形,你认为这个条件是_______(只填写序号). 题型三:利用菱形的性质求解 【变式1】如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE.∠E=50°,求∠BAO的大小. 【变式2】如图,四边形ABCD是菱形,AE⊥BC于点E,AF⊥CD于点F. (1)求证:△ABE≌△ADF; (2)若AE=4,CF=2,求菱形的边长. 【变式3】如图,是菱形的对角线. (1)作边的垂直平分线,分别与,交于点,(尺规作图,不写作法,保留作图痕迹); (2)在(1)的条件下,连接,若,求的度数. 题型四:菱形的判定证明 【变式1】如图,点,分别在的边,上,,连接,.请从以下三个条件:①;②;③中,选择一个合适的作为已知条件,使为菱形. (1)你添加的条件是______(填序号); (2)添加了条件后,请证明为菱形. 【变式2】如图,已知四边形是平行四边形,其对角线相交于点O,. (1)是直角三角形吗?请说明理由; (2)求证:四边形是菱形. 【变式3】如图,四边形是平行四边形,,且分别交对角线于点M,N,连接. (1)求证:; (2)若.求证:四边形是菱形.
小试牛刀
一、选择题(共5题) 1.矩形具有而菱形不一定具有的性质是( ) A.邻边相等 B.对角线相等 C.对角线互相平分 D.对角线互相垂直 2.下列命题中,是真命题的是( ) A.平行四边形是轴对称图形 B.对角线互相垂直的四边形是菱形 C.到一条线段两个端点距离相等的点,在这条线段的垂直平分线上 D.在中,若,则是直角三角形 3.如图,在菱形ABCD中,对角线AC,BD相交于点O,下列结论中错误的是( ) A.AB=AD B.AC⊥BD C.AC=BD D.∠DAC=∠BAC 4.如图,在平面直角坐标系中,菱形的顶点D在x轴上,边在y轴上,若点A的坐标为,则C点的坐标为( ) A. B. C. D. 5.如图,菱形的对边、上分别有两个动点M和N,若的最大值为,最小值为4,则菱形的面积为( ) A.18 B.28 C. D. 二、填空题(共5题) 6.点是菱形的对称中心,,连接,则的度数为 . 7.如图,菱形的对角线,相交于点,点是边的中点,若,则的长为 . 8.如图,在平面直角坐标系中,菱形的顶点在轴的正半轴上,点的坐标为,则点的坐标为 . 9.如图,菱形的边长为2,,对角线与交于点,为中点,为中点,连接,则的长为 . 10.如图,在菱形中,.若M、N分别是边上的动点,且,作,垂足分别为E、F,则的值为 . 三、解答题(共5题) 11.已知. (1)化简; (2)若,是菱形两条对角线的长,且该菱形的面积为,求的值. 12.如图,在四边形中,,,对角线交于点,平分,过点作交的延长线于点,连接. (1) 求证:四边形是菱形; (2) 若,,求的长. 13.如图,四边形是平行四边形,连接,交于点,平分交于点,平分交于点,连接,. (1)求证:; (2)若四边形是菱形且,,求四边形的面积. 14.如图,在矩形中,. 在图①中,P是上一点,垂直平分,分别交边于点E、F,求证:四边形是菱形; 若菱形的四个顶点都在矩形的边上,当菱形的面积最大时,菱形的边长是 . 15.综合与实践 问题情境:如图1,在中,,点D是的中点,连接,将沿直线折叠,点B落在点E处,连接. 独立思考: 在图1中,若,,则的长为______; 实践探究: 在图1中,请你判断与的位置关系,并说明理由; 问题解决: 如图2,在中,,,点D是的中点,连接,将沿直线折叠,点B落在点E处,连接.请判断四边形的形状,并说明理由.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
