2024年中考数学一轮复习专题讲义:一次函数(含答案)
文档属性
| 名称 | 2024年中考数学一轮复习专题讲义:一次函数(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 408.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-09 00:00:00 | ||
图片预览




文档简介
2024年中考数学一轮复习专题讲义:一次函数
知识点梳理
1、定义
定义1:一般地,形如y=kx(k是常数,k≠0)的函数叫做正比例函数,其中k叫做比例系数。
定义2:一般地,形如y=kx+b(k,b是常数,k≠0)的函数叫做一次函数。当b=0时,y=kx+b即y=kx,是正比例函数。所以说正比例函数是一种特殊的一次函数。
2、一次函数的图象及其性质
正比例函数的图象及性质:正比例函数y=kx(k是常数,k≠0)的图象是一条经过原点的直线,称为直线y=kx。
y=kx 图像 经过象限 升降趋势 增减性
k>0 三、一 从左向右上升 y随着x的增大而增大
k<0 二、四 从左向右下降 y随着x的增大而减小
一次函数的图象及性质:一次函数y=kx+b(k、b是常数,k≠0)的图象是一条直线,称为直线y=kx+b。当k>0时,直线y=kx+b从左向右上升,即y随着x的增大而增大;当k<0时,直线y=kx+b从左向右下降,即y随着x的增大而减小。
y=kx+b 图像 经过象限 升降趋势 增减性
k>0,b>0 三、二、一 从左向右上升 y随着x的增大而增大
k>0,b<0 三、四、一
k<0,b>0 二、一、四 从左向右下降 y随着x的增大而减小
k<0,b<0 二、三、四
3、待定系数法
定义:先设出函数解析式,再根据条件确定解析式中未知的系数,从而得出函数解析式的方法,叫做待定系数法。
4、一次函数与方程(组)及不等式(组)
方程(组)的解与相应函数的交点坐标是相对应的。找到函数的交点坐标,也就找到了对应方程(组)的解,反之一样。对于不等式(组)的解集也可以通过其对应的函数图象来解决。
配套练习
一、单选题
1.若正比例函数的图象经过点,则的值为( )
A. B. C. D.
2.已知直线经过第一、二、四象限,则k的取值范围是( )
A. B. C. D.
3.关于函数y=2x,下列结论中正确的是( )
A.函数图象经过点(2,1) B.函数图象经过第二、四象限
C.y随x的增大而增大 D.不论x取何值,总有y>0
4.,是一次函数图象上的两点,则下列正确的是( ).
A. B.
C.当时, D.当时,
5.对于正比例函数,它的函数值y随x的增大而增大,则一次函数的图象大致是( )
A.B. C.D.
6.一次函数分别交轴、轴于,两点,在轴上取一点,使为等腰三角形,则这样的点最多有几个( )
A.5 B.4 C.3 D.2
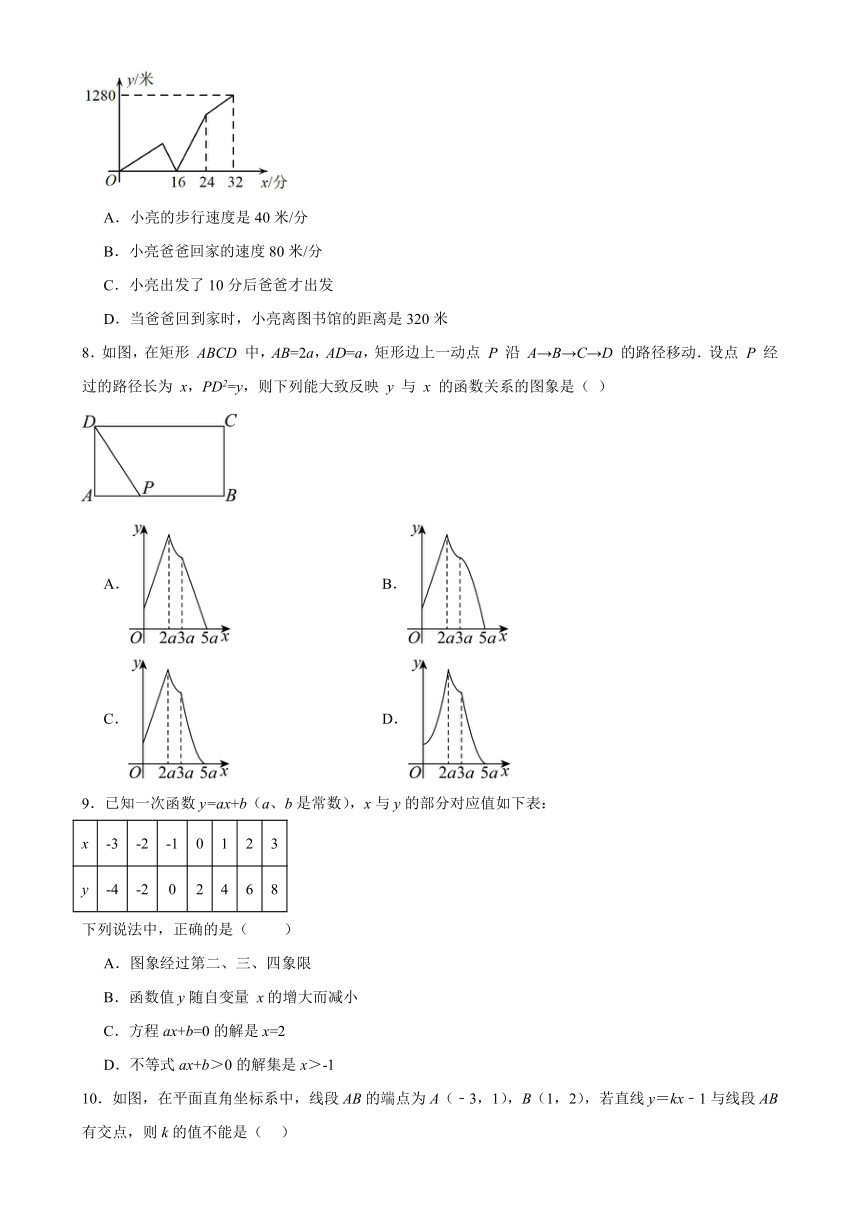
7.一天,小亮从家出发匀速步行去图书馆借书.几分钟后,在家休假的爸爸发现小亮忘带借书卡,于是爸爸骑自行车去追小亮,爸爸追上小亮以后以原速的一半回家.小亮拿到卡后以原速继续赶往图书馆,并从家出发后32分钟到达图书馆(小亮与爸爸交接时间忽略不计).两人相距的距离(米)与小亮步行所用时间(分钟)之间的函数关系如图所示,则下列说法错误的是( )
A.小亮的步行速度是40米/分
B.小亮爸爸回家的速度80米/分
C.小亮出发了10分后爸爸才出发
D.当爸爸回到家时,小亮离图书馆的距离是320米
8.如图,在矩形 ABCD 中,AB=2a,AD=a,矩形边上一动点 P 沿 A→B→C→D 的路径移动.设点 P 经过的路径长为 x,PD2=y,则下列能大致反映 y 与 x 的函数关系的图象是( )
A. B.
C. D.
9.已知一次函数y=ax+b(a、b是常数),x与y的部分对应值如下表:
x -3 -2 -1 0 1 2 3
y -4 -2 0 2 4 6 8
下列说法中,正确的是( )
A.图象经过第二、三、四象限
B.函数值y随自变量 x的增大而减小
C.方程ax+b=0的解是x=2
D.不等式ax+b>0的解集是x>-1
10.如图,在平面直角坐标系中,线段AB的端点为A(﹣3,1),B(1,2),若直线y=kx﹣1与线段AB有交点,则k的值不能是( )
A.2 B.4 C.﹣2 D.﹣4
二、填空题
11.已知函数y=2xm﹣1+1是一次函数,则m= .
12.平面直角坐标系中,已知点A(﹣1,﹣3)和点B(1,﹣2),则直线AB的解析式为 .
13.函数:中,自变量x的取值范围是 .
14.在平面直角坐标系xOy中,直线与x轴,y轴分别相交于A,B两点,若,则点A的坐标是 .
15.如图,一次图数与一次函数图象交于点,则关于的不等式组解集为 .
16.把直线y=-x-1沿x轴向右平移2个单位,所得直线的函数解析式是 .
17.直线y=mx+2m-1不经过第二象限,则m的取值范围是
18.已知直线y=x+2与函数y=的 图象交于A,B两点(点A在点B的左边).
(1)点A的坐标是 ;
(2)已知O是坐标原点,现把两个函数图象水平向右平移m个单位,点A,B平移后的对应点分别为A′,B′,连结OA′,OB′.当m= 时,|OA'﹣OB'|取最大值.
三、解答题
19.已知:是的函数,函数关系式为.
(1)当m为何值时,该函数是一次函数
(2)当m、n为何值时,该函数是正比例函数
(3)当m、n为何值时,该函数经过第一、二、三象限
20.如图,直线l:y1=﹣x﹣1与y轴交于点A,一次函数y2=x+3图象与y轴交于点B,与直线l交于点C,
(1)画出一次函数y2=x+3的图象;
(2)求点C坐标;
(3)如果y1>y2,那么x的取值范围是______.
21.某汽车制造公司计划生产A、B两种新型汽车共40辆投放到市场销售.已知A型汽车每辆成本34万元,售价39万元;B型汽车每辆成本42万元,售价50万元.若该公司对此项计划的投资不低于1536万元,不高于1552万元.请解答下列问题:
(1)该公司有哪几种生产方案?
(2)该公司按照哪种方案生产汽车,才能在这批汽车全部售出后,所获利润最大
(3)在(2)的情况下,公司决定拿出利润的全部用于生产甲乙两种钢板(两种都生产),乙钢板每吨6000元,共有多少种生产方案?
22.小亮、小明两人星期天8:00同时分别从A,B两地出发,沿同一条路线前往新华书店C.小明从B地步行出发,小亮骑自行车从A地出发途经B地,途中自行车发生故障,维修耽误了1 h,结果他俩11:00同时到达书店C.下图是他们距离A地的路程y(km)与所用时间x(h)之间的函数关系图象.请根据图中提供的信息,解答下列问题:
(1)求图中直线DE的函数解析式;
(2)若小亮的自行车不发生故障,且保持出发时的速度前行,则他出发多久可追上小明?此时他距离A地多远?
23.如图,直线l1:y1=-x+m与y轴交于点A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C,两条直线l1、l2相交于点D,连接AB.
(1)求两直线l1、l2交点D的坐标;
(2)求△ABD的面积.
参考答案:
1.B
2.B
3.C
4.D
5.C
6.B
7.C
8.D
9.D
10.A
11.2.
12.y=x﹣.
13.
14.或
15.
16.y=-x+1
17.0≤m≤
18. (1)联立,解得,则交点坐标为(),
联立,解得,则交点坐标为(),
又点A在点B的左边,所以A(),
故答案为:();
(2)当O、A′、B′三点共线时,|OA'﹣OB'|取最大值.
即直线平移后过原点即可,平移的距离为m,
平移后的直线为,
则,
解得,
当m=6时,|OA'﹣OB'|取最大值.
故答案为:6.
19.(1)解:该函数是一次函数,
,
;
(2)解:该函数是正比例函数,
且,
且;
(3)解:该函数经过第一、二、三象限,
,,
且.
20.解:(1)∵y2=x+3,
∴当y2=0时,x+3=0,解得x=﹣4,
当x=0时,y2=3,
∴直线y2=x+3与x轴的交点为(﹣4,0),与y轴的交点B的坐标为(0,3).
图象如下所示:
(2)解方程组,得,
则点C坐标为(﹣2,);
(3)如果y1>y2,那么x的取值范围是x<﹣2.
故答案为(1)画图见解析;(2)点C坐标为(﹣2,);(3)x<﹣2.
21.(1)解:设A型号的轿车为x辆,由题意得,
解得,
∵x是正整数,
∴或17或18.
有以下生产三种方案:
①生产A型号的轿车16辆,B型24辆;
②生产A型号的轿车17辆,B型23辆;
③生产A型号的轿车18辆,B型22辆.
(2)设所获利润为y元,由题意有:
,
∵y随x的增大而减小,
∴时,
∴,
∴最大利润272万元.
∴当生产A型号16辆,B型号24辆时,万元
(3)该公司的利润为:(万元),
设生产甲钢板m吨,乙钢板n吨,
则(m、n为整数),
化简得:,
当时,;
时,;
所以,甲钢板4吨,乙钢板8吨;甲钢板10吨,乙钢板3吨两种生产方案.
【点睛】此题考查了一次函数的应用,二元一次方程的应用,以及一元一次不等式组的应用,此题是典型的数学建模问题,要先将实际问题转化为不等式组解应用题.
22.解:(1)设直线DE的函数解析式为y=kx+b.易知点D的坐标为(3,22.5),点E的坐标为(1.5,7.5),∴解得∴直线DE的函数解析式为y=10x-7.5 (2)小明的速度为(22.5-10)÷3= (km/h).小亮出发时的速度为7.5÷0.5=15(km/h).设小亮出发m小时后追上小明,由题意,得m+10=15m,解得m=,当m=时,15×= (km).答:若小亮的自行车不发生故障,且保持出发时的速度前行,则他出发h可追上小明,此时他距离A地km
23.解:(1)将A(0,6)代入y1=-x+m得,m=6;
将B(-2,0)代入y2=kx+1得,k=,
组成方程组得,解得,
故D点坐标为(4,3);
(2)由y2=x+1可知,C点坐标为(0,1),
S△ABD=S△ABC+S△ACD=×5×2+×5×4=15.
知识点梳理
1、定义
定义1:一般地,形如y=kx(k是常数,k≠0)的函数叫做正比例函数,其中k叫做比例系数。
定义2:一般地,形如y=kx+b(k,b是常数,k≠0)的函数叫做一次函数。当b=0时,y=kx+b即y=kx,是正比例函数。所以说正比例函数是一种特殊的一次函数。
2、一次函数的图象及其性质
正比例函数的图象及性质:正比例函数y=kx(k是常数,k≠0)的图象是一条经过原点的直线,称为直线y=kx。
y=kx 图像 经过象限 升降趋势 增减性
k>0 三、一 从左向右上升 y随着x的增大而增大
k<0 二、四 从左向右下降 y随着x的增大而减小
一次函数的图象及性质:一次函数y=kx+b(k、b是常数,k≠0)的图象是一条直线,称为直线y=kx+b。当k>0时,直线y=kx+b从左向右上升,即y随着x的增大而增大;当k<0时,直线y=kx+b从左向右下降,即y随着x的增大而减小。
y=kx+b 图像 经过象限 升降趋势 增减性
k>0,b>0 三、二、一 从左向右上升 y随着x的增大而增大
k>0,b<0 三、四、一
k<0,b>0 二、一、四 从左向右下降 y随着x的增大而减小
k<0,b<0 二、三、四
3、待定系数法
定义:先设出函数解析式,再根据条件确定解析式中未知的系数,从而得出函数解析式的方法,叫做待定系数法。
4、一次函数与方程(组)及不等式(组)
方程(组)的解与相应函数的交点坐标是相对应的。找到函数的交点坐标,也就找到了对应方程(组)的解,反之一样。对于不等式(组)的解集也可以通过其对应的函数图象来解决。
配套练习
一、单选题
1.若正比例函数的图象经过点,则的值为( )
A. B. C. D.
2.已知直线经过第一、二、四象限,则k的取值范围是( )
A. B. C. D.
3.关于函数y=2x,下列结论中正确的是( )
A.函数图象经过点(2,1) B.函数图象经过第二、四象限
C.y随x的增大而增大 D.不论x取何值,总有y>0
4.,是一次函数图象上的两点,则下列正确的是( ).
A. B.
C.当时, D.当时,
5.对于正比例函数,它的函数值y随x的增大而增大,则一次函数的图象大致是( )
A.B. C.D.
6.一次函数分别交轴、轴于,两点,在轴上取一点,使为等腰三角形,则这样的点最多有几个( )
A.5 B.4 C.3 D.2
7.一天,小亮从家出发匀速步行去图书馆借书.几分钟后,在家休假的爸爸发现小亮忘带借书卡,于是爸爸骑自行车去追小亮,爸爸追上小亮以后以原速的一半回家.小亮拿到卡后以原速继续赶往图书馆,并从家出发后32分钟到达图书馆(小亮与爸爸交接时间忽略不计).两人相距的距离(米)与小亮步行所用时间(分钟)之间的函数关系如图所示,则下列说法错误的是( )
A.小亮的步行速度是40米/分
B.小亮爸爸回家的速度80米/分
C.小亮出发了10分后爸爸才出发
D.当爸爸回到家时,小亮离图书馆的距离是320米
8.如图,在矩形 ABCD 中,AB=2a,AD=a,矩形边上一动点 P 沿 A→B→C→D 的路径移动.设点 P 经过的路径长为 x,PD2=y,则下列能大致反映 y 与 x 的函数关系的图象是( )
A. B.
C. D.
9.已知一次函数y=ax+b(a、b是常数),x与y的部分对应值如下表:
x -3 -2 -1 0 1 2 3
y -4 -2 0 2 4 6 8
下列说法中,正确的是( )
A.图象经过第二、三、四象限
B.函数值y随自变量 x的增大而减小
C.方程ax+b=0的解是x=2
D.不等式ax+b>0的解集是x>-1
10.如图,在平面直角坐标系中,线段AB的端点为A(﹣3,1),B(1,2),若直线y=kx﹣1与线段AB有交点,则k的值不能是( )
A.2 B.4 C.﹣2 D.﹣4
二、填空题
11.已知函数y=2xm﹣1+1是一次函数,则m= .
12.平面直角坐标系中,已知点A(﹣1,﹣3)和点B(1,﹣2),则直线AB的解析式为 .
13.函数:中,自变量x的取值范围是 .
14.在平面直角坐标系xOy中,直线与x轴,y轴分别相交于A,B两点,若,则点A的坐标是 .
15.如图,一次图数与一次函数图象交于点,则关于的不等式组解集为 .
16.把直线y=-x-1沿x轴向右平移2个单位,所得直线的函数解析式是 .
17.直线y=mx+2m-1不经过第二象限,则m的取值范围是
18.已知直线y=x+2与函数y=的 图象交于A,B两点(点A在点B的左边).
(1)点A的坐标是 ;
(2)已知O是坐标原点,现把两个函数图象水平向右平移m个单位,点A,B平移后的对应点分别为A′,B′,连结OA′,OB′.当m= 时,|OA'﹣OB'|取最大值.
三、解答题
19.已知:是的函数,函数关系式为.
(1)当m为何值时,该函数是一次函数
(2)当m、n为何值时,该函数是正比例函数
(3)当m、n为何值时,该函数经过第一、二、三象限
20.如图,直线l:y1=﹣x﹣1与y轴交于点A,一次函数y2=x+3图象与y轴交于点B,与直线l交于点C,
(1)画出一次函数y2=x+3的图象;
(2)求点C坐标;
(3)如果y1>y2,那么x的取值范围是______.
21.某汽车制造公司计划生产A、B两种新型汽车共40辆投放到市场销售.已知A型汽车每辆成本34万元,售价39万元;B型汽车每辆成本42万元,售价50万元.若该公司对此项计划的投资不低于1536万元,不高于1552万元.请解答下列问题:
(1)该公司有哪几种生产方案?
(2)该公司按照哪种方案生产汽车,才能在这批汽车全部售出后,所获利润最大
(3)在(2)的情况下,公司决定拿出利润的全部用于生产甲乙两种钢板(两种都生产),乙钢板每吨6000元,共有多少种生产方案?
22.小亮、小明两人星期天8:00同时分别从A,B两地出发,沿同一条路线前往新华书店C.小明从B地步行出发,小亮骑自行车从A地出发途经B地,途中自行车发生故障,维修耽误了1 h,结果他俩11:00同时到达书店C.下图是他们距离A地的路程y(km)与所用时间x(h)之间的函数关系图象.请根据图中提供的信息,解答下列问题:
(1)求图中直线DE的函数解析式;
(2)若小亮的自行车不发生故障,且保持出发时的速度前行,则他出发多久可追上小明?此时他距离A地多远?
23.如图,直线l1:y1=-x+m与y轴交于点A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C,两条直线l1、l2相交于点D,连接AB.
(1)求两直线l1、l2交点D的坐标;
(2)求△ABD的面积.
参考答案:
1.B
2.B
3.C
4.D
5.C
6.B
7.C
8.D
9.D
10.A
11.2.
12.y=x﹣.
13.
14.或
15.
16.y=-x+1
17.0≤m≤
18. (1)联立,解得,则交点坐标为(),
联立,解得,则交点坐标为(),
又点A在点B的左边,所以A(),
故答案为:();
(2)当O、A′、B′三点共线时,|OA'﹣OB'|取最大值.
即直线平移后过原点即可,平移的距离为m,
平移后的直线为,
则,
解得,
当m=6时,|OA'﹣OB'|取最大值.
故答案为:6.
19.(1)解:该函数是一次函数,
,
;
(2)解:该函数是正比例函数,
且,
且;
(3)解:该函数经过第一、二、三象限,
,,
且.
20.解:(1)∵y2=x+3,
∴当y2=0时,x+3=0,解得x=﹣4,
当x=0时,y2=3,
∴直线y2=x+3与x轴的交点为(﹣4,0),与y轴的交点B的坐标为(0,3).
图象如下所示:
(2)解方程组,得,
则点C坐标为(﹣2,);
(3)如果y1>y2,那么x的取值范围是x<﹣2.
故答案为(1)画图见解析;(2)点C坐标为(﹣2,);(3)x<﹣2.
21.(1)解:设A型号的轿车为x辆,由题意得,
解得,
∵x是正整数,
∴或17或18.
有以下生产三种方案:
①生产A型号的轿车16辆,B型24辆;
②生产A型号的轿车17辆,B型23辆;
③生产A型号的轿车18辆,B型22辆.
(2)设所获利润为y元,由题意有:
,
∵y随x的增大而减小,
∴时,
∴,
∴最大利润272万元.
∴当生产A型号16辆,B型号24辆时,万元
(3)该公司的利润为:(万元),
设生产甲钢板m吨,乙钢板n吨,
则(m、n为整数),
化简得:,
当时,;
时,;
所以,甲钢板4吨,乙钢板8吨;甲钢板10吨,乙钢板3吨两种生产方案.
【点睛】此题考查了一次函数的应用,二元一次方程的应用,以及一元一次不等式组的应用,此题是典型的数学建模问题,要先将实际问题转化为不等式组解应用题.
22.解:(1)设直线DE的函数解析式为y=kx+b.易知点D的坐标为(3,22.5),点E的坐标为(1.5,7.5),∴解得∴直线DE的函数解析式为y=10x-7.5 (2)小明的速度为(22.5-10)÷3= (km/h).小亮出发时的速度为7.5÷0.5=15(km/h).设小亮出发m小时后追上小明,由题意,得m+10=15m,解得m=,当m=时,15×= (km).答:若小亮的自行车不发生故障,且保持出发时的速度前行,则他出发h可追上小明,此时他距离A地km
23.解:(1)将A(0,6)代入y1=-x+m得,m=6;
将B(-2,0)代入y2=kx+1得,k=,
组成方程组得,解得,
故D点坐标为(4,3);
(2)由y2=x+1可知,C点坐标为(0,1),
S△ABD=S△ABC+S△ACD=×5×2+×5×4=15.
同课章节目录
