9.4 矩形 菱形 正方形讲义苏科版八年级数学下册
文档属性
| 名称 | 9.4 矩形 菱形 正方形讲义苏科版八年级数学下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 550.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-09 11:00:24 | ||
图片预览




文档简介
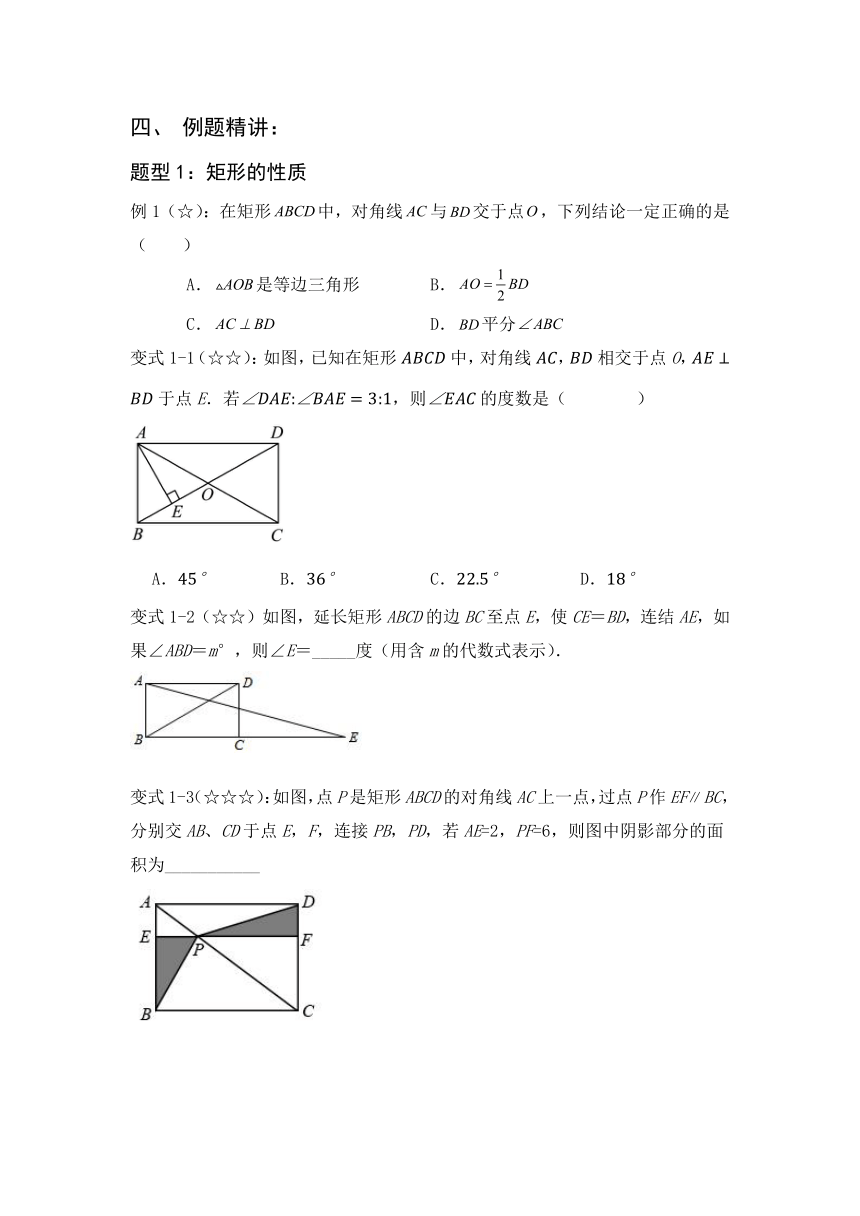
第二讲 矩形 菱形 正方形
教学目标:
1. 理解矩形、菱形、正方形的定义、性质、判定定理.
2、能运用矩形、菱形、正方形的相关定理完成证明或计算.
知识梳理:
知识要点:
要点一、矩形
1.定义:有一个角是直角的平行四边形叫做矩形.
2.性质:(1)具有平行四边形的所有性质;
(2)四个角都是直角;
(3)对角线互相平分且相等;
(4)中心对称图形,轴对称图形.
3.面积:
4.判定:(1) 有一个角是直角的平行四边形是矩形.
(2)对角线相等的平行四边形是矩形.
(3)有三个角是直角的四边形是矩形.
特别说明:由矩形得直角三角形的性质:
(1)直角三角形斜边上的中线等于斜边的一半;
(2)直角三角形中,30度角所对应的直角边等于斜边的一半.
要点二、菱形
1. 定义:有一组邻边相等的平行四边形叫做菱形.
2.性质:(1)具有平行四边形的一切性质;
(2)四条边相等;
(3)两条对角线互相平分且垂直,并且每一条对角线平分一组对角;
(4)中心对称图形,轴对称图形.
3.面积:
4.判定:(1)一组邻边相等的平行四边形是菱形;
(2)对角线互相垂直的平行四边形是菱形;
(3)四边相等的四边形是菱形.
要点三、正方形
1. 定义:一组邻边相等、并且有一个角是直角的平行四边形是正方形.
2.性质:(1)对边平行;
(2)四个角都是直角;
(3)四条边都相等;
(4)对角线互相垂直平分且相等,对角线平分对角;
(5) 两条对角线把正方形分成四个全等的等腰直角三角形;
(6)中心对称图形,轴对称图形.
3.面积:边长×边长=×对角线×对角线
4.判定:(1)有一个角是直角的菱形是正方形;
(2)一组邻边相等的矩形是正方形;
(3)对角线相等的菱形是正方形;
(4)对角线互相垂直的矩形是正方形;
(5)对角线互相垂直平分且相等的四边形是正方形;
(6)四条边都相等,四个角都是直角的四边形是正方形.
例题精讲:
题型1:矩形的性质
例1(☆):在矩形中,对角线与交于点,下列结论一定正确的是( )
A.是等边三角形 B.
C. D.平分
变式1-1(☆☆):如图,已知在矩形中,对角线,相交于点O,于点E.若,则的度数是( )
A. B. C. D.
变式1-2(☆☆)如图,延长矩形ABCD的边BC至点E,使CE=BD,连结AE,如果∠ABD=m°,则∠E=_____度(用含m的代数式表示).
变式1-3(☆☆☆):如图,点P是矩形ABCD的对角线AC上一点,过点P作EFBC,分别交AB、CD于点E,F,连接PB,PD,若AE=2,PF=6,则图中阴影部分的面积为___________
题型2:矩形的判定
例2(☆):已知平行四边形ABCD,下列条件中,不能判定这个平行四边形为矩形的是( )
A.∠A=∠B B.∠A=∠C C.AC=BD D.AB⊥BC
变式2-1(☆☆):如图,在中,对角线、相交于点,点、分别为、的中点.
(1)求证:;
(2)延长至,使,连接,延长,交于点,当时,试判断四边形是什么特殊的四边形,并说明理由.
变式2-2(☆☆☆):如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC=90°,对角线AC、BD交于点O,DE平分∠ADC交BC于点E,连接OE.
求证:四边形ABCD是矩形;
若∠BDE=15°,求∠EOC的度数;
在(2)的条件下,若AB=2,求矩形ABCD的面积.
题型3:菱形的性质
例3(☆):如图,在菱形中,,分别在,上,且,与交于点,连接.若,则的度数为( )
A. B. C. D.
变式3-1(☆☆):如图,在菱形ABCD中,AB=5,AC=8,则菱形的高为( )
A. B. C.12 D.24
变式3-2(☆☆☆):如图,在菱形ABCD中,∠A=100°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC的度数为( )
A.50° B.55° C.60° D.45°
题型4:菱形的判定
例4(☆):的对角线与相交于点,添加以下条件,不能判定平行四边形为菱形的是( )
A. B.
C. D.
变式4-1(☆☆):如图,中,已知是的平分线,E、F分别是边的中点,联结,要使四边形为菱形,需要满足一定的条件,该条件可以是______.
变式4-2(☆☆☆):在矩形纸片中,,.将矩形纸片折叠,使点与点重合.(1)连接,求证:四边形是菱形;(2)求折痕的长.
题型5:正方形的性质
例5(☆):如图,以正方形ABCD的对角线AC为一边作菱形AEFC,点F在DC的延长线上,连接AF交BC于点G,则∠FGC的度数为( )
A.67.5° B.45° C.60° D.75°
变式5-1(☆☆):如图,正方形ABCD中,AE=AB,直线DE交BC于点F,则∠BEF=( )
A.30° B.45° C.55° D.60°
变式5-2(☆☆☆):如图,已知正方形ABCD的边长为6,E为CD边上一点(点E不与端点C,D重合),将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF,对角线BD与AG、AE分别交于P、Q两点.以下各结论:①∠EAG=45°;②线段CF的最小值为6;③;④若DE=2,则G为BC的中点.正确的结论有( )个.
A.1 B.2 C.3 D.4
题型6:正方形的判定
例6(☆):如图,已知四边形ABCD是平行四边形,下列说法正确的是( )
A.若AB=AD,则 ABCD是矩形
B.若AB=AD,则 ABCD是正方形
C.若AB⊥BC,则 ABCD是矩形
D.若AC⊥BD,则 ABCD是正方形
变式6-1(☆☆):如图,△ABC的中线AF与中位线DE相交于点O.
(1)求证:AF与DE互相平分;
(2)当△ABC满足___________时,四边形ADFE是正方形.
变式6-2(☆☆☆):如图,点D为的边BC的中点,过点A作,且,连接DE,CE.
(1)求证:;
(2)若,判断四边形ADCE的形状,并说明理由;
(3)若要使四边形ADCE为正方形,则应满足什么条件?
(直接写出条件即可,不必证明).
强化练习:
1、如图,矩形的对角线相交于点,,若,则四边形的周长为( )
A.4 B.6 C.8 D.10
2、若菱形的较长对角线为24cm,面积为120cm2,则它的周长为( )
A.50cm B.51cm C.52cm D.56cm
3、如图,下列条件之一能使平行四边形ABCD是菱形的为( )
①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.
A.①③ B.②③ C.③④ D.①②③
4(☆☆☆)、在矩形ABCD中,对角线AC、BD相交于点O,AE平分交BC于点E,.连接OE,则下面的结论:①是等边三角形;②是等腰三角形;③;④;⑤,其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
5(☆☆☆)、如图.已知正方形ABCD的边长为12,BE=EC,将正方形的边CD沿DE折叠到DF,延长EF交AB于G,连接DG.现有如下3个结论;①AG+EC=GE;②∠GDE=45°;③△BGE的周长是24.其中正确的个数为( )
A.0 B.1 C.2 D.3
6(☆☆)、如图,将正方形ABCD沿BE对折,使点A落在对角线BD上的A′处,连接A′C,则∠BA′C=________度.
7(☆☆☆)、如图,将两张长为18,宽为6的矩形纸条交叉,可知重叠部分是一个__________形(图形形状),那么该图形周长的最大值与最小值的差等于__________.
8、如图,在中,对角线AC与BD相交于点O,点E,F在BD上,且,连接AE并延长,交BC于点G,连接CF并延长,交AD于点H.
(1)求证:;
(2)若AC平分,判断四边形AGCH的形状,并证明你的结论.
9(☆☆☆)、如图①,在长方形ABCD中,已知AB=20,AD=12,动点P从点D出发,以每秒2个单位的速度沿线段DC向终点C运动,运动时间为t秒,连接AP,设点D关于AP的对称点为点E.(1)如图②,射线PE恰好经过点B,试求此时t的值.
(2)当射线PE与边AB交于点Q时,①请直接写出AQ长的取值范围: ;
②是否存在这样的t的值,使得QE=QB?若存在,请求出所有符合题意的t的值;若不存在,请说明理由.
10(☆☆☆)、如图,在平行四边形中,的平分线交于点,交的延长线于F,以为邻边作平行四边形.(1)证明平行四边形是菱形;
(2)若,连结,①求证:;②求的度数;
(3)若,,,M是的中点,求的长.
课后作业:
1、(☆)(梅苑期中)下列说法中,正确的是( )
A. 顺次连接平行四边形各边中点所得到的四边形是矩形
B. 正方形的对角线互相垂直平分且相等
C. 矩形是轴对称图形且有四条对称轴
D. 菱形的对角线相等
2(☆☆)、(梅苑期中)如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在的直线上,得到经过点D的折痕DE.则∠DEC的大小为( )
A. 78° B. 75° C. 60° D. 45°
3、(☆☆)(广陵期中)如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )
A. 75° B. 60° C. 55° D. 45°
4、(☆☆)(邗江期末)如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE⊥BD,垂足为点E,若∠EAC=2∠CAD,则∠BAE=__________度.
5、(梅岭期中)如图,在菱形ABCD中,点E在CD上,若AE=AC,∠B=48°,则∠BAE的大小为_____.
6、(☆☆)(梅苑期中)如图,在正方形ABCD内,以AB为边作等边△ABE,则∠BEG=_____°.
7、(广陵期中)如图,矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为____.
8、(☆☆)(高邮期中)如图,在矩形ABCD中,BE平分,交CD于点E,点M、N分别是BE、AB的中点,连接MN,若,,则CD的长为______________.
9、(☆☆)(邗江期中)如图,菱形ABCD的对角线AC、BD相交于点O,,,OE与AB交于点F.(1)求证:四边形AEBO为矩形;(2)若OE=10,AC=16,求菱形ABCD面积.
10、(梅岭期中)如图,已知是矩形的对角线,的垂直平分线分别交、于点和,交于点.
(1)求证:四边形是菱形:
(2)若,,求四边形的周长.
11、(梅苑期中)如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AG是△ABC的外角∠FAC的平分线,DE∥AB,交AG于点E.求证:四边形ADCE是矩形.
12、(梅苑期中)如图,在四边形中,对角线、交于点O,,平分,过点C作交的延长线于点E,连接.
(1)求证:四边形是菱形;
(2)若,,求的长.
13、(☆☆☆)(广陵期中)知识再现:已知,如图,四边形ABCD是正方形,点M、N分别在边BC、CD上,连接AM、AN、MN,∠MAN=45°,延长CB至G使BG=DN,连接AG,根据三角形全等的知识,我们可以证明MN=BM+DN.
知识探究:(1)在如图中,作AH⊥MN,垂足为点H,猜想AH与AB有什么数量关系?并证明;
知识应用:(2)如图,已知∠BAC=45°,AD⊥BC于点D,且BD=2,AD=6,则CD的长为 ;
知识拓展:(3)如图,四边形ABCD是正方形,E是边BC的中点,F为边CD上一点,∠FEC=2∠BAE,AB=24,求DF的长.
14、(☆☆☆)(树人期中)如图1,P为Rt△ABC所在平面内任意一点(不在直线AC上),∠ACB=90°,M为AB边中点.操作:以PA、PC为邻边作平行四边形PADC,连结PM并延长到点E,使ME=PM,连结DE.
(1)请你利用图2,选择Rt△ABC内的任意一点P按上述方法操作;
(2)经历(1)之后,观察两图形,猜想线段DE和线段BC之间有怎样的数量和位置关系?请选择其中的一个图形证明你的猜想;
(3)观察两图,你还可得出AC和DE相关的什么结论?请说明理由.
(4)若以A为坐标原点,建立平面直角坐标系,其中A、C、D的坐标分别为(0,0),(5,3),(4,2),能否在平面内找到一点M,使以A、C、D、M为点构造成平行四边形,若不能,说明理由,若能,请直接写出点M的坐标.
教学目标:
1. 理解矩形、菱形、正方形的定义、性质、判定定理.
2、能运用矩形、菱形、正方形的相关定理完成证明或计算.
知识梳理:
知识要点:
要点一、矩形
1.定义:有一个角是直角的平行四边形叫做矩形.
2.性质:(1)具有平行四边形的所有性质;
(2)四个角都是直角;
(3)对角线互相平分且相等;
(4)中心对称图形,轴对称图形.
3.面积:
4.判定:(1) 有一个角是直角的平行四边形是矩形.
(2)对角线相等的平行四边形是矩形.
(3)有三个角是直角的四边形是矩形.
特别说明:由矩形得直角三角形的性质:
(1)直角三角形斜边上的中线等于斜边的一半;
(2)直角三角形中,30度角所对应的直角边等于斜边的一半.
要点二、菱形
1. 定义:有一组邻边相等的平行四边形叫做菱形.
2.性质:(1)具有平行四边形的一切性质;
(2)四条边相等;
(3)两条对角线互相平分且垂直,并且每一条对角线平分一组对角;
(4)中心对称图形,轴对称图形.
3.面积:
4.判定:(1)一组邻边相等的平行四边形是菱形;
(2)对角线互相垂直的平行四边形是菱形;
(3)四边相等的四边形是菱形.
要点三、正方形
1. 定义:一组邻边相等、并且有一个角是直角的平行四边形是正方形.
2.性质:(1)对边平行;
(2)四个角都是直角;
(3)四条边都相等;
(4)对角线互相垂直平分且相等,对角线平分对角;
(5) 两条对角线把正方形分成四个全等的等腰直角三角形;
(6)中心对称图形,轴对称图形.
3.面积:边长×边长=×对角线×对角线
4.判定:(1)有一个角是直角的菱形是正方形;
(2)一组邻边相等的矩形是正方形;
(3)对角线相等的菱形是正方形;
(4)对角线互相垂直的矩形是正方形;
(5)对角线互相垂直平分且相等的四边形是正方形;
(6)四条边都相等,四个角都是直角的四边形是正方形.
例题精讲:
题型1:矩形的性质
例1(☆):在矩形中,对角线与交于点,下列结论一定正确的是( )
A.是等边三角形 B.
C. D.平分
变式1-1(☆☆):如图,已知在矩形中,对角线,相交于点O,于点E.若,则的度数是( )
A. B. C. D.
变式1-2(☆☆)如图,延长矩形ABCD的边BC至点E,使CE=BD,连结AE,如果∠ABD=m°,则∠E=_____度(用含m的代数式表示).
变式1-3(☆☆☆):如图,点P是矩形ABCD的对角线AC上一点,过点P作EFBC,分别交AB、CD于点E,F,连接PB,PD,若AE=2,PF=6,则图中阴影部分的面积为___________
题型2:矩形的判定
例2(☆):已知平行四边形ABCD,下列条件中,不能判定这个平行四边形为矩形的是( )
A.∠A=∠B B.∠A=∠C C.AC=BD D.AB⊥BC
变式2-1(☆☆):如图,在中,对角线、相交于点,点、分别为、的中点.
(1)求证:;
(2)延长至,使,连接,延长,交于点,当时,试判断四边形是什么特殊的四边形,并说明理由.
变式2-2(☆☆☆):如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC=90°,对角线AC、BD交于点O,DE平分∠ADC交BC于点E,连接OE.
求证:四边形ABCD是矩形;
若∠BDE=15°,求∠EOC的度数;
在(2)的条件下,若AB=2,求矩形ABCD的面积.
题型3:菱形的性质
例3(☆):如图,在菱形中,,分别在,上,且,与交于点,连接.若,则的度数为( )
A. B. C. D.
变式3-1(☆☆):如图,在菱形ABCD中,AB=5,AC=8,则菱形的高为( )
A. B. C.12 D.24
变式3-2(☆☆☆):如图,在菱形ABCD中,∠A=100°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC的度数为( )
A.50° B.55° C.60° D.45°
题型4:菱形的判定
例4(☆):的对角线与相交于点,添加以下条件,不能判定平行四边形为菱形的是( )
A. B.
C. D.
变式4-1(☆☆):如图,中,已知是的平分线,E、F分别是边的中点,联结,要使四边形为菱形,需要满足一定的条件,该条件可以是______.
变式4-2(☆☆☆):在矩形纸片中,,.将矩形纸片折叠,使点与点重合.(1)连接,求证:四边形是菱形;(2)求折痕的长.
题型5:正方形的性质
例5(☆):如图,以正方形ABCD的对角线AC为一边作菱形AEFC,点F在DC的延长线上,连接AF交BC于点G,则∠FGC的度数为( )
A.67.5° B.45° C.60° D.75°
变式5-1(☆☆):如图,正方形ABCD中,AE=AB,直线DE交BC于点F,则∠BEF=( )
A.30° B.45° C.55° D.60°
变式5-2(☆☆☆):如图,已知正方形ABCD的边长为6,E为CD边上一点(点E不与端点C,D重合),将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF,对角线BD与AG、AE分别交于P、Q两点.以下各结论:①∠EAG=45°;②线段CF的最小值为6;③;④若DE=2,则G为BC的中点.正确的结论有( )个.
A.1 B.2 C.3 D.4
题型6:正方形的判定
例6(☆):如图,已知四边形ABCD是平行四边形,下列说法正确的是( )
A.若AB=AD,则 ABCD是矩形
B.若AB=AD,则 ABCD是正方形
C.若AB⊥BC,则 ABCD是矩形
D.若AC⊥BD,则 ABCD是正方形
变式6-1(☆☆):如图,△ABC的中线AF与中位线DE相交于点O.
(1)求证:AF与DE互相平分;
(2)当△ABC满足___________时,四边形ADFE是正方形.
变式6-2(☆☆☆):如图,点D为的边BC的中点,过点A作,且,连接DE,CE.
(1)求证:;
(2)若,判断四边形ADCE的形状,并说明理由;
(3)若要使四边形ADCE为正方形,则应满足什么条件?
(直接写出条件即可,不必证明).
强化练习:
1、如图,矩形的对角线相交于点,,若,则四边形的周长为( )
A.4 B.6 C.8 D.10
2、若菱形的较长对角线为24cm,面积为120cm2,则它的周长为( )
A.50cm B.51cm C.52cm D.56cm
3、如图,下列条件之一能使平行四边形ABCD是菱形的为( )
①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.
A.①③ B.②③ C.③④ D.①②③
4(☆☆☆)、在矩形ABCD中,对角线AC、BD相交于点O,AE平分交BC于点E,.连接OE,则下面的结论:①是等边三角形;②是等腰三角形;③;④;⑤,其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
5(☆☆☆)、如图.已知正方形ABCD的边长为12,BE=EC,将正方形的边CD沿DE折叠到DF,延长EF交AB于G,连接DG.现有如下3个结论;①AG+EC=GE;②∠GDE=45°;③△BGE的周长是24.其中正确的个数为( )
A.0 B.1 C.2 D.3
6(☆☆)、如图,将正方形ABCD沿BE对折,使点A落在对角线BD上的A′处,连接A′C,则∠BA′C=________度.
7(☆☆☆)、如图,将两张长为18,宽为6的矩形纸条交叉,可知重叠部分是一个__________形(图形形状),那么该图形周长的最大值与最小值的差等于__________.
8、如图,在中,对角线AC与BD相交于点O,点E,F在BD上,且,连接AE并延长,交BC于点G,连接CF并延长,交AD于点H.
(1)求证:;
(2)若AC平分,判断四边形AGCH的形状,并证明你的结论.
9(☆☆☆)、如图①,在长方形ABCD中,已知AB=20,AD=12,动点P从点D出发,以每秒2个单位的速度沿线段DC向终点C运动,运动时间为t秒,连接AP,设点D关于AP的对称点为点E.(1)如图②,射线PE恰好经过点B,试求此时t的值.
(2)当射线PE与边AB交于点Q时,①请直接写出AQ长的取值范围: ;
②是否存在这样的t的值,使得QE=QB?若存在,请求出所有符合题意的t的值;若不存在,请说明理由.
10(☆☆☆)、如图,在平行四边形中,的平分线交于点,交的延长线于F,以为邻边作平行四边形.(1)证明平行四边形是菱形;
(2)若,连结,①求证:;②求的度数;
(3)若,,,M是的中点,求的长.
课后作业:
1、(☆)(梅苑期中)下列说法中,正确的是( )
A. 顺次连接平行四边形各边中点所得到的四边形是矩形
B. 正方形的对角线互相垂直平分且相等
C. 矩形是轴对称图形且有四条对称轴
D. 菱形的对角线相等
2(☆☆)、(梅苑期中)如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在的直线上,得到经过点D的折痕DE.则∠DEC的大小为( )
A. 78° B. 75° C. 60° D. 45°
3、(☆☆)(广陵期中)如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )
A. 75° B. 60° C. 55° D. 45°
4、(☆☆)(邗江期末)如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE⊥BD,垂足为点E,若∠EAC=2∠CAD,则∠BAE=__________度.
5、(梅岭期中)如图,在菱形ABCD中,点E在CD上,若AE=AC,∠B=48°,则∠BAE的大小为_____.
6、(☆☆)(梅苑期中)如图,在正方形ABCD内,以AB为边作等边△ABE,则∠BEG=_____°.
7、(广陵期中)如图,矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为____.
8、(☆☆)(高邮期中)如图,在矩形ABCD中,BE平分,交CD于点E,点M、N分别是BE、AB的中点,连接MN,若,,则CD的长为______________.
9、(☆☆)(邗江期中)如图,菱形ABCD的对角线AC、BD相交于点O,,,OE与AB交于点F.(1)求证:四边形AEBO为矩形;(2)若OE=10,AC=16,求菱形ABCD面积.
10、(梅岭期中)如图,已知是矩形的对角线,的垂直平分线分别交、于点和,交于点.
(1)求证:四边形是菱形:
(2)若,,求四边形的周长.
11、(梅苑期中)如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AG是△ABC的外角∠FAC的平分线,DE∥AB,交AG于点E.求证:四边形ADCE是矩形.
12、(梅苑期中)如图,在四边形中,对角线、交于点O,,平分,过点C作交的延长线于点E,连接.
(1)求证:四边形是菱形;
(2)若,,求的长.
13、(☆☆☆)(广陵期中)知识再现:已知,如图,四边形ABCD是正方形,点M、N分别在边BC、CD上,连接AM、AN、MN,∠MAN=45°,延长CB至G使BG=DN,连接AG,根据三角形全等的知识,我们可以证明MN=BM+DN.
知识探究:(1)在如图中,作AH⊥MN,垂足为点H,猜想AH与AB有什么数量关系?并证明;
知识应用:(2)如图,已知∠BAC=45°,AD⊥BC于点D,且BD=2,AD=6,则CD的长为 ;
知识拓展:(3)如图,四边形ABCD是正方形,E是边BC的中点,F为边CD上一点,∠FEC=2∠BAE,AB=24,求DF的长.
14、(☆☆☆)(树人期中)如图1,P为Rt△ABC所在平面内任意一点(不在直线AC上),∠ACB=90°,M为AB边中点.操作:以PA、PC为邻边作平行四边形PADC,连结PM并延长到点E,使ME=PM,连结DE.
(1)请你利用图2,选择Rt△ABC内的任意一点P按上述方法操作;
(2)经历(1)之后,观察两图形,猜想线段DE和线段BC之间有怎样的数量和位置关系?请选择其中的一个图形证明你的猜想;
(3)观察两图,你还可得出AC和DE相关的什么结论?请说明理由.
(4)若以A为坐标原点,建立平面直角坐标系,其中A、C、D的坐标分别为(0,0),(5,3),(4,2),能否在平面内找到一点M,使以A、C、D、M为点构造成平行四边形,若不能,说明理由,若能,请直接写出点M的坐标.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
