第十章 三角形的有关证明 4 线段的垂直平分线 第1课时 线段垂直平分线及其作图(含答案)
文档属性
| 名称 | 第十章 三角形的有关证明 4 线段的垂直平分线 第1课时 线段垂直平分线及其作图(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-09 12:32:57 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第十章 三角形的有关证明
4 线段的垂直平分线
第1课时 线段垂直平分线及其作图
基 础 练
知识点一 线段垂直平分线的性质及判定
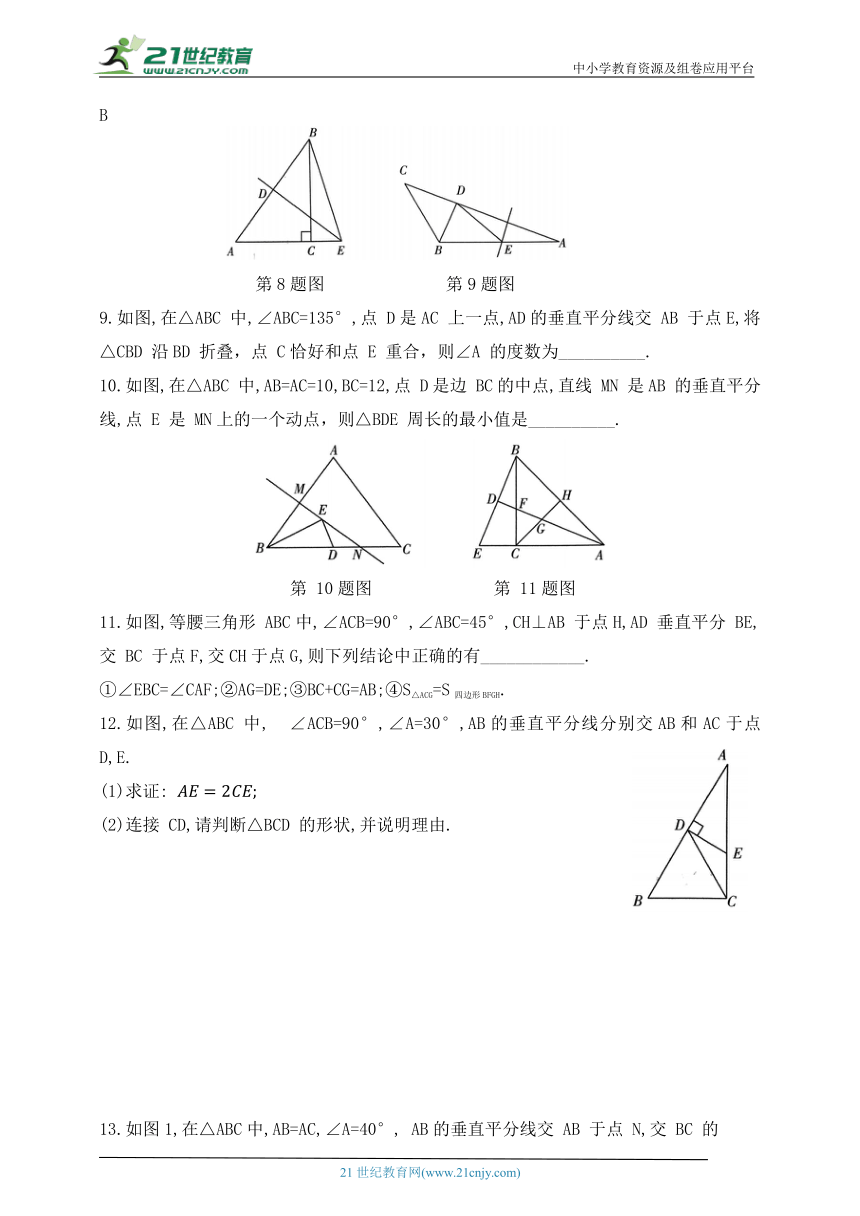
1.如图,直线 CD是线段AB 的垂直平分线,P 为直线CD上的一点,已知线段 PA=3cm,则线段 PB的长为 ( )
A. 6 cm B. 5 cm C.4 cm D.3 cm
第 1题图 第 2题图
2.如图,在四边形 ABCD 中,AC 与BD交于点E,AB=AD,CB=CD,下列结论不一定成立的是 ( )
A. AC 平分∠BAD B. AC 垂直平分 BD
C.△BEC≌△DEC D. AB=BD
3.如图,在△ABC 中,DE 是 AC 的垂直平分线,且分别交 BC,AC 于点 D 和E,∠B=60°,∠C=25°,则∠BAD= ( )
A.50° B.70° C.75° D.80°
第 3 题图 第4 题图
4.如图,在△ABC中,DE 是AC 的垂直平分线,分别交 AC,AB 于点 D, E,若△BCE的周长为 16,BC=6,则 AB 的长为___________.
5.如图,AF 平分∠BAC,点P 是 AF 上任意一点,过点 P 向AB,AC 作垂线段 PD,PE,垂足分别为点 D,E,连接DE.求证:AF 垂直平分 DE.
6.如图,在 中, AC,DE是 AB 的垂直平分线,垂足为点 D, 交 AC 于点E.
(1)若 ,求∠EBC的度数;
(2)若△ABC 的周长为 43 cm,BC 的长为11 cm,求△BCE的周长.
知识点二 作线段的垂直平分线
7.如图,在△ABC 中,AB=AC,分别以点 B 和点 C 为圆心,大于 的长为半径作弧,两弧交于点 D,作直线 AD 交BC 于点E.若∠BAC=110°,则∠ABE的度数为__________.
提 升 练
8.如图,在 Rt△ABC 中,∠ACB=90°,AC=3,BC=4,斜边 AB的垂直平分线 DE 交AB 于点D,交 AC 的延长线于点E,连接 BE,则 DE的长为 ( )
A. B. C.
B
第8题图 第9题图
9.如图,在△ABC 中,∠ABC=135°,点 D是AC 上一点,AD的垂直平分线交 AB 于点E,将△CBD 沿BD 折叠,点 C恰好和点 E 重合,则∠A 的度数为__________.
10.如图,在△ABC 中,AB=AC=10,BC=12,点 D是边 BC的中点,直线 MN 是AB 的垂直平分线,点 E 是 MN上的一个动点,则△BDE 周长的最小值是__________.
第 10题图 第 11题图
11.如图,等腰三角形 ABC中,∠ACB=90°,∠ABC=45°,CH⊥AB 于点H,AD 垂直平分 BE,交 BC 于点F,交CH于点G,则下列结论中正确的有____________.
①∠EBC=∠CAF;②AG=DE;③BC+CG=AB;④S△ACG=S四边形BFGH.
12.如图,在△ABC 中, ∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点 D,E.
(1)求证:
(2)连接 CD,请判断△BCD 的形状,并说明理由.
13.如图1,在△ABC中,AB=AC,∠A=40°, AB的垂直平分线交 AB 于点 N,交 BC 的
延长线于点M.
(1)求∠NMB的度数;
(2)如图2,如果将(1)中∠A 的度数改为70°,其余条件不变,再求∠NMB 的度数;
(3)根据(1)(2)的计算,你能发现其中蕴含的规律吗 请写出你的猜想并证明;
(4)如图3,将(1)中的∠A改为钝角,其余条件不变,该规律是否需要加以修改 请你把∠A代入一个钝角度数验证你的结论.
参考答案
1. D 2. D 3. B 4.10
5.证明:∵AF平分∠BAC,PD⊥AB,PE⊥AC, ∴PD=PE,∠ADP=∠AEP=90°,
在 Rt△ADP 和 Rt△AEP中,
∴Rt△ADP≌Rt△AEP(HL),∴AD=AE,
∵PD=PE,∴AF 垂直平分 DE.
6.解:(1)∵DE 垂直平分AB,∴AE=BE,∴∠A=∠ABE=50°,
又∵AB=AC,∴∠ABC=∠ACB,
而∠A+∠ABC+∠ACB=180°,
∴∠EBC=∠ABC-∠ABE=65°-50°=15°.
(2)∵△ABC 的周长为 43 cm,BC=11 cm,∴AB=AC=16 cm,
又∵DE 垂直平分AB,∴EA=EB,
∴△BCE的周长为BC+BE+CE=BC+AE+CE=BC+AC=16+11=27 cm.
7.35° 8. B 9.15° 10.14 11.①③
12.(1)证明:连接 BE,如图所示.
∵DE 是AB 的垂直平分线,∴AE=BE.∴∠ABE=∠A=30°.
∴∠CBE=∠ABC-∠ABE=30°.∴在 Rt△BCE 中,BE=2CE.∴AE=2CE.
(2)解:△BCD是等边三角形.
理由:由题意,知 D 为 AB 的中点.
∵∠ACB=90°,∴CD=BD.
∵∠ABC=60°,∴△BCD是等边三角形.
13.解:(1)∵在△ABC中,AB=AC,∠A=40°,∴∠B=70°.
∵MN是 AB 的垂直平分线,∴∠BNM=90°,∴∠NMB=90°-∠B=20°.
(2)∵在△ABC中,AB=AC,∠A=70°,∴∠B=55°.
∵MN是AB 的垂直平分线,∴∠BNM=90°,∴∠NMB=90°-∠B=35°.
(3)能,猜想:
证明:在△ABC中,
∵MN 是 AB 的垂直平分线,
(4)不需要修改.
验证(代入度数不唯一):若
∵在 中,
∵MN 是 AB 的垂直平分线,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第十章 三角形的有关证明
4 线段的垂直平分线
第1课时 线段垂直平分线及其作图
基 础 练
知识点一 线段垂直平分线的性质及判定
1.如图,直线 CD是线段AB 的垂直平分线,P 为直线CD上的一点,已知线段 PA=3cm,则线段 PB的长为 ( )
A. 6 cm B. 5 cm C.4 cm D.3 cm
第 1题图 第 2题图
2.如图,在四边形 ABCD 中,AC 与BD交于点E,AB=AD,CB=CD,下列结论不一定成立的是 ( )
A. AC 平分∠BAD B. AC 垂直平分 BD
C.△BEC≌△DEC D. AB=BD
3.如图,在△ABC 中,DE 是 AC 的垂直平分线,且分别交 BC,AC 于点 D 和E,∠B=60°,∠C=25°,则∠BAD= ( )
A.50° B.70° C.75° D.80°
第 3 题图 第4 题图
4.如图,在△ABC中,DE 是AC 的垂直平分线,分别交 AC,AB 于点 D, E,若△BCE的周长为 16,BC=6,则 AB 的长为___________.
5.如图,AF 平分∠BAC,点P 是 AF 上任意一点,过点 P 向AB,AC 作垂线段 PD,PE,垂足分别为点 D,E,连接DE.求证:AF 垂直平分 DE.
6.如图,在 中, AC,DE是 AB 的垂直平分线,垂足为点 D, 交 AC 于点E.
(1)若 ,求∠EBC的度数;
(2)若△ABC 的周长为 43 cm,BC 的长为11 cm,求△BCE的周长.
知识点二 作线段的垂直平分线
7.如图,在△ABC 中,AB=AC,分别以点 B 和点 C 为圆心,大于 的长为半径作弧,两弧交于点 D,作直线 AD 交BC 于点E.若∠BAC=110°,则∠ABE的度数为__________.
提 升 练
8.如图,在 Rt△ABC 中,∠ACB=90°,AC=3,BC=4,斜边 AB的垂直平分线 DE 交AB 于点D,交 AC 的延长线于点E,连接 BE,则 DE的长为 ( )
A. B. C.
B
第8题图 第9题图
9.如图,在△ABC 中,∠ABC=135°,点 D是AC 上一点,AD的垂直平分线交 AB 于点E,将△CBD 沿BD 折叠,点 C恰好和点 E 重合,则∠A 的度数为__________.
10.如图,在△ABC 中,AB=AC=10,BC=12,点 D是边 BC的中点,直线 MN 是AB 的垂直平分线,点 E 是 MN上的一个动点,则△BDE 周长的最小值是__________.
第 10题图 第 11题图
11.如图,等腰三角形 ABC中,∠ACB=90°,∠ABC=45°,CH⊥AB 于点H,AD 垂直平分 BE,交 BC 于点F,交CH于点G,则下列结论中正确的有____________.
①∠EBC=∠CAF;②AG=DE;③BC+CG=AB;④S△ACG=S四边形BFGH.
12.如图,在△ABC 中, ∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点 D,E.
(1)求证:
(2)连接 CD,请判断△BCD 的形状,并说明理由.
13.如图1,在△ABC中,AB=AC,∠A=40°, AB的垂直平分线交 AB 于点 N,交 BC 的
延长线于点M.
(1)求∠NMB的度数;
(2)如图2,如果将(1)中∠A 的度数改为70°,其余条件不变,再求∠NMB 的度数;
(3)根据(1)(2)的计算,你能发现其中蕴含的规律吗 请写出你的猜想并证明;
(4)如图3,将(1)中的∠A改为钝角,其余条件不变,该规律是否需要加以修改 请你把∠A代入一个钝角度数验证你的结论.
参考答案
1. D 2. D 3. B 4.10
5.证明:∵AF平分∠BAC,PD⊥AB,PE⊥AC, ∴PD=PE,∠ADP=∠AEP=90°,
在 Rt△ADP 和 Rt△AEP中,
∴Rt△ADP≌Rt△AEP(HL),∴AD=AE,
∵PD=PE,∴AF 垂直平分 DE.
6.解:(1)∵DE 垂直平分AB,∴AE=BE,∴∠A=∠ABE=50°,
又∵AB=AC,∴∠ABC=∠ACB,
而∠A+∠ABC+∠ACB=180°,
∴∠EBC=∠ABC-∠ABE=65°-50°=15°.
(2)∵△ABC 的周长为 43 cm,BC=11 cm,∴AB=AC=16 cm,
又∵DE 垂直平分AB,∴EA=EB,
∴△BCE的周长为BC+BE+CE=BC+AE+CE=BC+AC=16+11=27 cm.
7.35° 8. B 9.15° 10.14 11.①③
12.(1)证明:连接 BE,如图所示.
∵DE 是AB 的垂直平分线,∴AE=BE.∴∠ABE=∠A=30°.
∴∠CBE=∠ABC-∠ABE=30°.∴在 Rt△BCE 中,BE=2CE.∴AE=2CE.
(2)解:△BCD是等边三角形.
理由:由题意,知 D 为 AB 的中点.
∵∠ACB=90°,∴CD=BD.
∵∠ABC=60°,∴△BCD是等边三角形.
13.解:(1)∵在△ABC中,AB=AC,∠A=40°,∴∠B=70°.
∵MN是 AB 的垂直平分线,∴∠BNM=90°,∴∠NMB=90°-∠B=20°.
(2)∵在△ABC中,AB=AC,∠A=70°,∴∠B=55°.
∵MN是AB 的垂直平分线,∴∠BNM=90°,∴∠NMB=90°-∠B=35°.
(3)能,猜想:
证明:在△ABC中,
∵MN 是 AB 的垂直平分线,
(4)不需要修改.
验证(代入度数不唯一):若
∵在 中,
∵MN 是 AB 的垂直平分线,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
