北京市十一晋元中学元梦2023-2024学年第二学期初三数学周练试卷一(2024.3.8)(PDF版无答案)
文档属性
| 名称 | 北京市十一晋元中学元梦2023-2024学年第二学期初三数学周练试卷一(2024.3.8)(PDF版无答案) |

|
|
| 格式 | |||
| 文件大小 | 655.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-09 00:00:00 | ||
图片预览

文档简介
北京十一晋元中学元梦初三数学周练一(2024.3.8) 8.某产品的盈利额(即产品的销售价格与固定成本之差)记为 y,购买人数记为 x,其函数图象如图 1所示.由于日前该
考试时间:120分钟 满分:100分 产品盈利未达到预期,相关人员提出了两种调整方案,如图 2,图 3中的实线分别为调整后 y与 x的函数图象.给出下
注意事项: 列四种说法,其中正确说法的序号是( )
1.本试卷共 4页,共三道大题,28道小题.
2.试题答案一律填涂或书写在答题卡上,在试卷上作答无效.
一、选择题(每题 2分,共 16分)
1.2023年 3月 21日,北京市统计局、国家统计局北京调查总队发布《北京市 2022年国民经济和社会发展统计公报》.数
据显示,2022年末北京全市常住人口为 2184.3万人,比上年末减少 4.3万人.将 2184.3万用科学记数法表示为( )
A.2184.3×104 B.2.1843×104 C.2.1843×108 D.2.1843×107
2.如图图形中既是轴对称图形又是中心对称图形的是( ) ①图 2对应的方案是:保持销售价格不变,并降低成本;
②图 2对应的方案是:提高销售价格,并提高成本;
③图 3对应的方案是:提高销售价格,并降低成本;
④图 3对应的方案是:提高销售价格,并保持成本不变.
A. B. C. D. A.①③ B.②③ C.①④ D.②④
3.实数 a,b,c,d在数轴上对应的点的位置如图所示,下列结论正确的是( ) 二、填空题(每题 2分,共 16分)
9 1.若二次根式 有意义,则 x的取值范围是 .
x 1
A.a+c>0 B.d﹣a>0 C.|a|<|b| D.ad>0 10.因式分解:8mn﹣2mn3= .
4.下列计算正确的是( ) 11.写出一个一元二次方程,使得此方程有两个不相等的实数根,此方程为 .
A.(﹣3x3)3=27x9 B.(1﹣x)2=1﹣2x+x2 C.y8÷y2=y4 D.(a+b)2=a2+b2 12.正方形网格中,∠AOB如图放置,则 sin∠AOB=____________.
5.如图,已知在四边形 ABCD中,DE⊥BC,BD平分∠ABC,AB=6,DE=4,则△ABD的面积是( )
A.24 B.18 C.12 D.6
6.“二十四节气”是中华上古农耕文明的智慧结晶,被国际气象界誉为“中国第五大发明”.若要从“立春”“立夏”“秋分”“大寒” 第 12题图 第 13题图 第 14题图
四张邮票中抽取两张,则恰好抽到“立夏”、“秋分”两张邮票的概率是( ) 13.如图,AB是⊙O的直径,∠D=40°,则∠AOC= .
1 1 1 3
A. B. C. D.
2 3 6 4 14.如图,在 Rt△ABC中,∠C=90°,∠ABC=30°, BC 3 ,将△ABC绕点 A逆时针旋转角α(0°<α<180°)得到
7.观察下列尺规作图的痕迹,能够说明 AB>AC的是( ) △AB'C',并使点 C'落在 AB边上.
(1)旋转角α的度数是 .
(2)线段 AB所扫过部分的面积是 .(结果保留π)
15.2022年 10月 16日上午,举世瞩目的中共二十大召开.非凡十年、沧桑巨变.我国人均 GDP从约 3.6万元增加到 8.1
万元(新华网).假如每一个 5 年里人均增长率不变,则人均增长率约为多少?设人均增长率为 x,根据题意可列方
程 .
A.①③ B.②③ C.①② D.③④
第 1 页
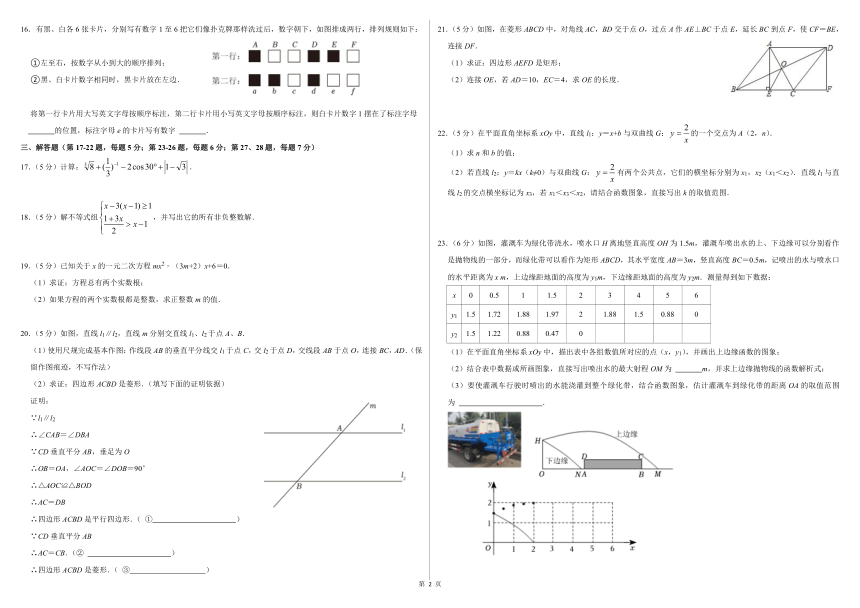
16.有黑、白各 6张卡片,分别写有数字 1至 6把它们像扑克牌那样洗过后,数字朝下,如图排成两行,排列规则如下: 21.(5分)如图,在菱形 ABCD中,对角线 AC,BD交于点 O,过点 A作 AE⊥BC于点 E,延长 BC到点 F,使 CF=BE,
连接 DF.
①左至右,按数字从小到大的顺序排列; (1)求证:四边形 AEFD是矩形;
②黑、白卡片数字相同时,黑卡片放在左边. (2)连接 OE,若 AD=10,EC=4,求 OE的长度.
将第一行卡片用大写英文字母按顺序标注,第二行卡片用小写英文字母按顺序标注,则白卡片数字 1摆在了标注字母
的位置,标注字母 e的卡片写有数字 . 222.(5分)在平面直角坐标系 xOy中,直线 l1:y=x+b与双曲线 G: y 的一个交点为 A(2,n).
x
三、解答题(第 17-22题,每题 5分;第 23-26题,每题 6分;第 27、28题,每题 7分)
(1)求 n和 b的值;
1
17 1.(5分)计算: 3 8 ( ) 2cos30 1 3 . y 23 (2)若直线 l2:y=kx(k≠0)与双曲线 G: 有两个公共点,它们的横坐标分别为 x1,x2(x1<x2).直线 l1与直x
线 l2的交点横坐标记为 x3,若 x1<x3<x2,请结合函数图象,直接写出 k的取值范围.
x 3(x 1) 1
18.(5 分)解不等式组 1 3x ,并写出它的所有非负整数解.
x 1 2
23.(6分)如图,灌溉车为绿化带浇水,喷水口 H离地竖直高度 OH为 1.5m,灌溉车喷出水的上、下边缘可以分别看作
2 是抛物线的一部分,而绿化带可以看作为矩形 ABCD,其水平宽度 AB=3m,竖直高度 BC=0.5m,记喷出的水与喷水口19.(5分)已知关于 x的一元二次方程 mx ﹣(3m+2)x+6=0.
的水平距离为 x m,上边缘距地面的高度为 y
1 1
m,下边缘距地面的高度为 y2m.测量得到如下数据:
( )求证:方程总有两个实数根;
2 m x 0 0.5 1 1.5 2 3 4 5 6( )如果方程的两个实数根都是整数,求正整数 的值.
y1 1.5 1.72 1.88 1.97 2 1.88 1.5 0.88 0
20.(5分)如图,直线 l1∥l2,直线 m分别交直线 l1、l2于点 A、B. y2 1.5 1.22 0.88 0.47 0
(1)使用尺规完成基本作图:作线段 AB的垂直平分线交 l1于点 C,交 l2于点 D,交线段 AB于点 O,连接 BC,AD.(保 (1)在平面直角坐标系 xOy中,描出表中各组数值所对应的点(x,y1),并画出上边缘函数的图象;
留作图痕迹,不写作法) (2)结合表中数据或所画图象,直接写出喷出水的最大射程 OM为 m,并求上边缘抛物线的函数解析式;
(2)求证:四边形 ACBD是菱形.(填写下面的证明依据) (3)要使灌溉车行驶时喷出的水能浇灌到整个绿化带,结合函数图象,估计灌溉车到绿化带的距离 OA的取值范围
证明: 为 .
∵l1∥l2
∴∠CAB=∠DBA
∵CD垂直平分 AB,垂足为 O
∴OB=OA,∠AOC=∠DOB=90°
∴△AOC≌△BOD
∴AC=DB
∴四边形 ACBD是平行四边形.( ① )
∵CD垂直平分 AB
∴AC=CB.(② )
∴四边形 ACBD是菱形.( ③ )
第 2 页
24.(6分)为了深入学习领会党的二十大精神,某校团委组织了两次“二十大知识竞赛”.从中随机抽取了 30名学生两次 25.(6 分)如图,在△ABC中,∠ACB=90°,点 D是 AB边的中点,点 O在 AC边上,以点 O为圆心,OC为半径画
竞赛成绩(百分制)的数据,并对数据(成绩)进行整理、描述和分析.下面给出了部分信息: ⊙O,⊙O与 AB边相切于点 E,过点 A作 AF∥CD.
a.两次竞赛学生成绩情况统计图: (1)求证:AF是⊙O的切线;
b.两次竞赛学生的获奖情况如下: 4(2)若 BC=6,sin B= ,求⊙O的半径及 OD的长.
5
奖项竞赛 参与奖 优秀奖 卓越奖
第一次竞赛 人数 8 m n
平均分 73 85 95
第二次竞赛 人数 9 5 16
平均分 74 85 93
(说明:成绩≥90,获卓越奖;80≤成绩<90,获优秀奖;成绩<80,获参与奖)
c.第二次竞赛获卓越奖的学生成绩如下:90 90 91 91 91 91 92 93 93 94 94 94 95 95 96 98,
根据以上信息,回答下列问题:
26.(6分)在平面直角坐标系中,设二次函数 y=(x+a)(x﹣a﹣1)(a>0),
(1)写出表中 m,n的值;
(1)直接写出二次函数的对称轴;
(2)甲同学第一次竞赛成绩是 83分,第二次竞赛成绩是 96分,在图中用“〇”圈出代表甲同学的点;
(2)若当﹣1≤x≤3时,函数的最大值为 4,求此二次函数的顶点坐标.
(3)下列推断合理的是 .
(3)抛物线上两点 M(x1,y1),N(x2,y2)若对于 t<x1<t+1,t+2<x2<t+3都有 y1≠y2,求 t的取值范围.
①第二次竞赛成绩数据的中位数是 90;
②两次竞赛都获得卓越奖的有 10人;
③第二次竞赛的平均成绩高于第一次竞赛的平均成绩.
第 3 页
27.(7分)在△ABC中,AB=AC,∠BAC=90°,过点 A作 BC的垂线 AD,垂足为 D,E为射线 DC上一动点(不与点 28.(7分)在平面内,C为线段 AB外的一点,若以点 A,B,C为顶点的三角形为直角三角形,则称 C为线段 AB的直角
C重合),连接 AE,以点 A为中心,将线段 AE逆时针旋转 90°得到线段 AF,连接 BF,与直线 AD交于点 G. 点.特别地,当该三角形为等腰直角三角形时,称 C为线段 AB的等腰直角点.
(1)如图 1,当点 E在线段 CD上时, (1)如图 1,在平面直角坐标系 xOy中,点 M的坐标为(﹣1,0),点 N的坐标为(1,0),在点 P1(2,1),P2(﹣1,
①依题意补全图形; 3 1
2),P3( , )中,线段 MN的直角点是 ;
②求证:点 G为 BF的中点. 2 2
(2)如图 2,当点 E在线段 DC的延长线上时,用等式表示 CE,AG之间的数量关系,并证明.
(2)在平面直角坐标系 xOy中,点 A,B的坐标分别为(t,0),(0,4).
①若 t=4,如图 2所示,若 C是线段 AB的直角点,且点 C在直线 y=﹣x+8上,求点 C的坐标;
②如图 3,点 D的坐标为(m,﹣2),⊙D的半径为 1,若⊙D上存在线段 AB的等腰直角点,直接写出 m的取值范围.
第 4 页
考试时间:120分钟 满分:100分 产品盈利未达到预期,相关人员提出了两种调整方案,如图 2,图 3中的实线分别为调整后 y与 x的函数图象.给出下
注意事项: 列四种说法,其中正确说法的序号是( )
1.本试卷共 4页,共三道大题,28道小题.
2.试题答案一律填涂或书写在答题卡上,在试卷上作答无效.
一、选择题(每题 2分,共 16分)
1.2023年 3月 21日,北京市统计局、国家统计局北京调查总队发布《北京市 2022年国民经济和社会发展统计公报》.数
据显示,2022年末北京全市常住人口为 2184.3万人,比上年末减少 4.3万人.将 2184.3万用科学记数法表示为( )
A.2184.3×104 B.2.1843×104 C.2.1843×108 D.2.1843×107
2.如图图形中既是轴对称图形又是中心对称图形的是( ) ①图 2对应的方案是:保持销售价格不变,并降低成本;
②图 2对应的方案是:提高销售价格,并提高成本;
③图 3对应的方案是:提高销售价格,并降低成本;
④图 3对应的方案是:提高销售价格,并保持成本不变.
A. B. C. D. A.①③ B.②③ C.①④ D.②④
3.实数 a,b,c,d在数轴上对应的点的位置如图所示,下列结论正确的是( ) 二、填空题(每题 2分,共 16分)
9 1.若二次根式 有意义,则 x的取值范围是 .
x 1
A.a+c>0 B.d﹣a>0 C.|a|<|b| D.ad>0 10.因式分解:8mn﹣2mn3= .
4.下列计算正确的是( ) 11.写出一个一元二次方程,使得此方程有两个不相等的实数根,此方程为 .
A.(﹣3x3)3=27x9 B.(1﹣x)2=1﹣2x+x2 C.y8÷y2=y4 D.(a+b)2=a2+b2 12.正方形网格中,∠AOB如图放置,则 sin∠AOB=____________.
5.如图,已知在四边形 ABCD中,DE⊥BC,BD平分∠ABC,AB=6,DE=4,则△ABD的面积是( )
A.24 B.18 C.12 D.6
6.“二十四节气”是中华上古农耕文明的智慧结晶,被国际气象界誉为“中国第五大发明”.若要从“立春”“立夏”“秋分”“大寒” 第 12题图 第 13题图 第 14题图
四张邮票中抽取两张,则恰好抽到“立夏”、“秋分”两张邮票的概率是( ) 13.如图,AB是⊙O的直径,∠D=40°,则∠AOC= .
1 1 1 3
A. B. C. D.
2 3 6 4 14.如图,在 Rt△ABC中,∠C=90°,∠ABC=30°, BC 3 ,将△ABC绕点 A逆时针旋转角α(0°<α<180°)得到
7.观察下列尺规作图的痕迹,能够说明 AB>AC的是( ) △AB'C',并使点 C'落在 AB边上.
(1)旋转角α的度数是 .
(2)线段 AB所扫过部分的面积是 .(结果保留π)
15.2022年 10月 16日上午,举世瞩目的中共二十大召开.非凡十年、沧桑巨变.我国人均 GDP从约 3.6万元增加到 8.1
万元(新华网).假如每一个 5 年里人均增长率不变,则人均增长率约为多少?设人均增长率为 x,根据题意可列方
程 .
A.①③ B.②③ C.①② D.③④
第 1 页
16.有黑、白各 6张卡片,分别写有数字 1至 6把它们像扑克牌那样洗过后,数字朝下,如图排成两行,排列规则如下: 21.(5分)如图,在菱形 ABCD中,对角线 AC,BD交于点 O,过点 A作 AE⊥BC于点 E,延长 BC到点 F,使 CF=BE,
连接 DF.
①左至右,按数字从小到大的顺序排列; (1)求证:四边形 AEFD是矩形;
②黑、白卡片数字相同时,黑卡片放在左边. (2)连接 OE,若 AD=10,EC=4,求 OE的长度.
将第一行卡片用大写英文字母按顺序标注,第二行卡片用小写英文字母按顺序标注,则白卡片数字 1摆在了标注字母
的位置,标注字母 e的卡片写有数字 . 222.(5分)在平面直角坐标系 xOy中,直线 l1:y=x+b与双曲线 G: y 的一个交点为 A(2,n).
x
三、解答题(第 17-22题,每题 5分;第 23-26题,每题 6分;第 27、28题,每题 7分)
(1)求 n和 b的值;
1
17 1.(5分)计算: 3 8 ( ) 2cos30 1 3 . y 23 (2)若直线 l2:y=kx(k≠0)与双曲线 G: 有两个公共点,它们的横坐标分别为 x1,x2(x1<x2).直线 l1与直x
线 l2的交点横坐标记为 x3,若 x1<x3<x2,请结合函数图象,直接写出 k的取值范围.
x 3(x 1) 1
18.(5 分)解不等式组 1 3x ,并写出它的所有非负整数解.
x 1 2
23.(6分)如图,灌溉车为绿化带浇水,喷水口 H离地竖直高度 OH为 1.5m,灌溉车喷出水的上、下边缘可以分别看作
2 是抛物线的一部分,而绿化带可以看作为矩形 ABCD,其水平宽度 AB=3m,竖直高度 BC=0.5m,记喷出的水与喷水口19.(5分)已知关于 x的一元二次方程 mx ﹣(3m+2)x+6=0.
的水平距离为 x m,上边缘距地面的高度为 y
1 1
m,下边缘距地面的高度为 y2m.测量得到如下数据:
( )求证:方程总有两个实数根;
2 m x 0 0.5 1 1.5 2 3 4 5 6( )如果方程的两个实数根都是整数,求正整数 的值.
y1 1.5 1.72 1.88 1.97 2 1.88 1.5 0.88 0
20.(5分)如图,直线 l1∥l2,直线 m分别交直线 l1、l2于点 A、B. y2 1.5 1.22 0.88 0.47 0
(1)使用尺规完成基本作图:作线段 AB的垂直平分线交 l1于点 C,交 l2于点 D,交线段 AB于点 O,连接 BC,AD.(保 (1)在平面直角坐标系 xOy中,描出表中各组数值所对应的点(x,y1),并画出上边缘函数的图象;
留作图痕迹,不写作法) (2)结合表中数据或所画图象,直接写出喷出水的最大射程 OM为 m,并求上边缘抛物线的函数解析式;
(2)求证:四边形 ACBD是菱形.(填写下面的证明依据) (3)要使灌溉车行驶时喷出的水能浇灌到整个绿化带,结合函数图象,估计灌溉车到绿化带的距离 OA的取值范围
证明: 为 .
∵l1∥l2
∴∠CAB=∠DBA
∵CD垂直平分 AB,垂足为 O
∴OB=OA,∠AOC=∠DOB=90°
∴△AOC≌△BOD
∴AC=DB
∴四边形 ACBD是平行四边形.( ① )
∵CD垂直平分 AB
∴AC=CB.(② )
∴四边形 ACBD是菱形.( ③ )
第 2 页
24.(6分)为了深入学习领会党的二十大精神,某校团委组织了两次“二十大知识竞赛”.从中随机抽取了 30名学生两次 25.(6 分)如图,在△ABC中,∠ACB=90°,点 D是 AB边的中点,点 O在 AC边上,以点 O为圆心,OC为半径画
竞赛成绩(百分制)的数据,并对数据(成绩)进行整理、描述和分析.下面给出了部分信息: ⊙O,⊙O与 AB边相切于点 E,过点 A作 AF∥CD.
a.两次竞赛学生成绩情况统计图: (1)求证:AF是⊙O的切线;
b.两次竞赛学生的获奖情况如下: 4(2)若 BC=6,sin B= ,求⊙O的半径及 OD的长.
5
奖项竞赛 参与奖 优秀奖 卓越奖
第一次竞赛 人数 8 m n
平均分 73 85 95
第二次竞赛 人数 9 5 16
平均分 74 85 93
(说明:成绩≥90,获卓越奖;80≤成绩<90,获优秀奖;成绩<80,获参与奖)
c.第二次竞赛获卓越奖的学生成绩如下:90 90 91 91 91 91 92 93 93 94 94 94 95 95 96 98,
根据以上信息,回答下列问题:
26.(6分)在平面直角坐标系中,设二次函数 y=(x+a)(x﹣a﹣1)(a>0),
(1)写出表中 m,n的值;
(1)直接写出二次函数的对称轴;
(2)甲同学第一次竞赛成绩是 83分,第二次竞赛成绩是 96分,在图中用“〇”圈出代表甲同学的点;
(2)若当﹣1≤x≤3时,函数的最大值为 4,求此二次函数的顶点坐标.
(3)下列推断合理的是 .
(3)抛物线上两点 M(x1,y1),N(x2,y2)若对于 t<x1<t+1,t+2<x2<t+3都有 y1≠y2,求 t的取值范围.
①第二次竞赛成绩数据的中位数是 90;
②两次竞赛都获得卓越奖的有 10人;
③第二次竞赛的平均成绩高于第一次竞赛的平均成绩.
第 3 页
27.(7分)在△ABC中,AB=AC,∠BAC=90°,过点 A作 BC的垂线 AD,垂足为 D,E为射线 DC上一动点(不与点 28.(7分)在平面内,C为线段 AB外的一点,若以点 A,B,C为顶点的三角形为直角三角形,则称 C为线段 AB的直角
C重合),连接 AE,以点 A为中心,将线段 AE逆时针旋转 90°得到线段 AF,连接 BF,与直线 AD交于点 G. 点.特别地,当该三角形为等腰直角三角形时,称 C为线段 AB的等腰直角点.
(1)如图 1,当点 E在线段 CD上时, (1)如图 1,在平面直角坐标系 xOy中,点 M的坐标为(﹣1,0),点 N的坐标为(1,0),在点 P1(2,1),P2(﹣1,
①依题意补全图形; 3 1
2),P3( , )中,线段 MN的直角点是 ;
②求证:点 G为 BF的中点. 2 2
(2)如图 2,当点 E在线段 DC的延长线上时,用等式表示 CE,AG之间的数量关系,并证明.
(2)在平面直角坐标系 xOy中,点 A,B的坐标分别为(t,0),(0,4).
①若 t=4,如图 2所示,若 C是线段 AB的直角点,且点 C在直线 y=﹣x+8上,求点 C的坐标;
②如图 3,点 D的坐标为(m,﹣2),⊙D的半径为 1,若⊙D上存在线段 AB的等腰直角点,直接写出 m的取值范围.
第 4 页
同课章节目录
