高考数学考点概括(苏教版)
图片预览









文档简介
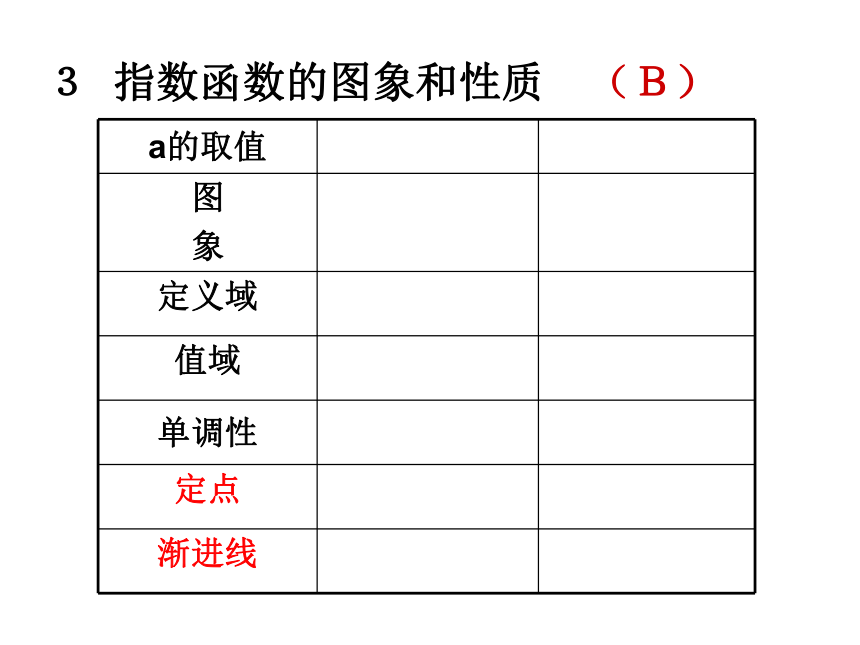
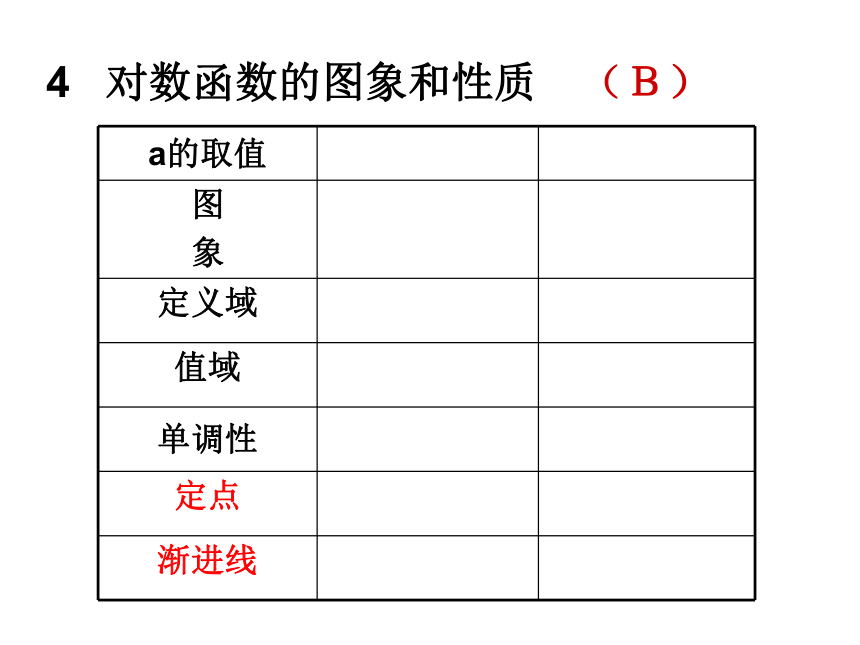
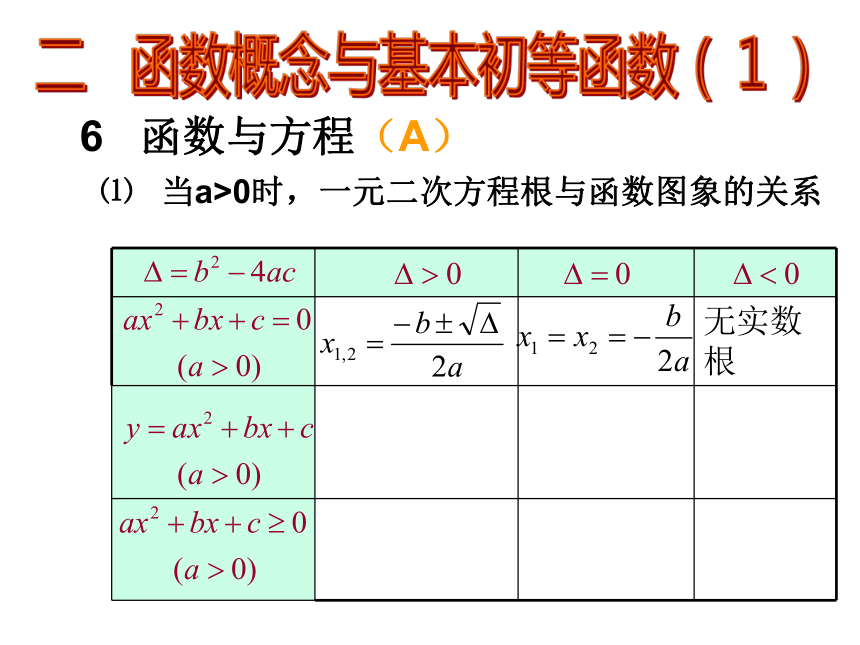
课件139张PPT。09高考总复习——知识篇一 集合 1 集合及其表示 (A)列举法 描述法元素: 确定性 互异性 无序性2 子集 (B)⑴⑵3 交集、并集、补集 (B)二 函数概念与基本初等函数(1) 1 函数的有关概念 (B)非空数集“每一个”到“惟一”⑵分段函数概念⑴①②二 函数概念与基本初等函数(1) 2 函数的基本性质 (B)①②定义域值域⑶单调性任取-作差-化简、变形-定号两个单调区间一般不能用“U”连接⑷奇偶性⑴⑵①考察定义域是否关于原点对称②奇函数特有 f(0)=0⑸周期性⑹对称性①②①②二 函数概念与基本初等函数(1) ③3 指数函数的图象和性质 (B)4 对数函数的图象和性质 (B)5 幂函数(A)二 函数概念与基本初等函数(1) ⑴研究幂函数,主要靠图象;⑵几点说明:1) 确定定义域2) 确定奇偶性可能会起到事半功倍的效果3) 判断图象的形状1) 图象必过点 (1,1)2) 在第四象限没有图象6 函数与方程(A)二 函数概念与基本初等函数(1) ⑴当a>0时,一元二次方程根与函数图象的关系二 函数概念与基本初等函数(1) ⑵二分法1) 函数的图象是连续的2) 通过图象初步确定根所在的区间3) 利用二分法解决问题7 函数模型及其应用 (B)二 函数概念与基本初等函数(1) ⑴实际问题中的自变量取值的合理性⑵三 基本初等函数(2)三角恒等变换 1 三角函数的有关概念 (B)定义 抓住x , y , r符号 一全二正三切四余三角函数线 正切线的起点特殊2 同角三角函数的基本关系式 (B)⑶⑴⑵三 基本初等函数(2)三角恒等变换 3 正、余弦的诱导公式 (B)公式一(相同)公式二公式三公式四公式五公式六4 三角函数的图象和性质 (B)三 基本初等函数(2)三角恒等变换 初相变换(相位变换)振幅变换周期变换(A)⑶⑴⑵三 基本初等函数(2)三角恒等变换 6 两角和(差)的正弦、余弦和正切(C)典型应用:6 两角和(差)的正弦、余弦和正切(C)三 基本初等函数(2)三角恒等变换 典型应用:三 基本初等函数(2)三角恒等变换 7 二倍角的正弦、余弦和正切 (B)三 基本初等函数(2)三角恒等变换 8 几个三角恒等式 (A)⑴半角公式⑵万能代换公式四 解三角形1 正弦定理及其应用 (B)四 解三角形2 余弦定理及其应用 (B)五 平面向量1 平面向量的有关概念 (B)⑴向量的概念:既有大小又有方向的量称为 向量①②⑵向量的表示方法:几何表示法字母表示法⑶向量的模:向量的大小称为向量的长度(模)五 平面向量⑷两个特殊向量:零向量模为0,方向不确定.② 单位向量:长度为 1 个单位长度的向量.单位向量模为1,方向不一定相同.⑸平行向量、共线向量:①②平行向量又称共线向量;规定零向量与任一向量平行。⑹相等向量、相反向量:五 平面向量①②相等向量 长度相等且方向相同的向量相反向量 长度相等且方向相反的向量五 平面向量2 平面向量的线性运算 (B)⑴向量的加法:①②三角形法则、平行四边形法则⑵向量的减法:①②三角形法则、平行四边形法则五 平面向量⑶向量的数乘:1)概念 一般地,我们规定实数λ与向量 的积是一个向量,这种运算叫做向量的数乘,记作 ,它的长度和方向规定如下:五 平面向量2) 共线定理O五 平面向量3 平面向量的坐标 表示 (B)⑴ 向量的坐标表示B终点的坐标减去起点的坐标A(x ,y)五 平面向量⑵ 向量的坐标运算五 平面向量4 平面向量的数量积 (C)⑴ 数量积的定义①②③两个向量的数量积是一个数量,而不是向量.注意a·b不能写成a×b,a×b 表示向量的另一种运算.五 平面向量⑵ 数量积的坐标表示⑶ 数量积的几何意义⑷ 数量积的主要性质数量积积为零是判定两向量垂直的充要条件用于计算向量的模用于计算向量的夹角这就是平面内两点间的距离公式(1)e · a=a · e=| a | cos? 五 平面向量⑸ 数量积的运算律①交换律:②对数乘的结合律:③分配律:注意:数量积不满足结合律,即:方向不同五 平面向量5 平面向量的平行与垂直(B)⑴ 平行(即共线)⑵ 垂直五 平面向量6 平面向量的应用 (A)1 数列的有关概念 (A)六 数列 六 数列 2 等差数列 (C)⑴ 相关概念①②③公差d对数列的影响若d>0,则为递增数列若d=0,则为常数数列若d>0,则为递减数列前n项和通项公式六 数列 ⑵ 判定方法①②③六 数列 ⑶ 常用性质①②③六 数列 ⑶ 常用性质④⑤⑥六 数列 ⑶ 常用性质⑦a)b)c)a)b)c)六 数列 3 等比数列 (C)⑴ 相关概念①公比q对数列的影响六 数列 ②③前n项和通项公式六 数列 ⑵ 判定方法①②③六 数列 ⑶ 常用性质①②③六 数列 ⑶ 常用性质④⑤⑥六 数列 ⑶ 常用性质⑧⑦六 数列 补充 数列通项与前n项和 (C)⑴ 数列的通项①归纳法: 依据前几项 (不唯一)②等差与等比数列 套用公式③④⑤六 数列 ⑥⑵ 数列的前n项和六 数列 ①公式法②倒序相加法 (等差数列的公式推导)③④错位相减法 (等比数列的公式推导)裂项相消法 六 数列 ④裂项相消法 几种常见形式 : 七 不等式 1 基本不等式 (C)⑴⑵总之:一正二定三相等七 不等式 2 一元二次不等式 (C)当a<0时,方程函数不等式关系七 不等式 3 线性规划 (A)通用步骤:定线------定界------定域方法①七 不等式 方法② 选点法 (直线定界,特殊点定域)方法③ 与系数B相关法见教材P77 练习3认真理解z与直线截距间的关系注意八 复数 1 复数的有关概念(B)⑴ 引入新数 i,叫虚数单位。规定: i2= -1C复数集:a叫复数Z的实部,记作ReZb叫复数Z的虚部,记作ImZ八 复数 ⑵ 复数的分类八 复数 2 复数的四则运算(B)⑴ 复数的加减乘除复数 z1=a+bi, z2=c+di,(a,b,c,d是实数)
z1+z2=(a+c)+(b+d)i;
z1-z2=(a-c)+(b-d)i.( a + bi )( c + di ) = ( ac – bd ) + ( bc + ad )i.八 复数 2 复数的四则运算(B)⑵ 复数的乘方八 复数 2 复数的四则运算(B)⑶ 共轭复数注:1)当a=0时,共轭复数也称为共轭虚数;
2)实数的共轭复数是它本身。八 复数 2 复数的四则运算(B)⑶ 共轭复数八 复数 2 复数的四则运算(B)⑷ 常用运算性质1)2)八 复数 2 复数的四则运算(B)⑷ 常用运算性质3)八 复数 2 复数的四则运算(B)⑷ 常用运算性质4)八 复数 3 复数的几何意义(A)向量 的模叫做复数z的模,记为则几何意义: 复平面内该点到原点的距离。模的运算性质:模的拓展性质复平面的两点间距离公式①以 对应的点为圆心,r为半径的圆。八 复数 3 复数的几何意义(A)八 复数 3 复数的几何意义(A)②以 对应的点为端点的线段的中垂线;③④以 对应的点为焦点的椭圆;以 对应的点为焦点的双曲线。九 导数及其应用1 导数的概念(A)⑴ 平均变化率⑵ 瞬时变化率——导数①②③曲线上一点处切线的斜率瞬时速度瞬时加速度导数⑶ 求导的一般步骤九 导数及其应用2 导数的几何意义 (B)曲线上一点处切线的斜率3 导数的运算 (B)⑴ 常见函数的导数九 导数及其应用⑵ 导数的运算法则九 导数及其应用⑶ 简单的复合导数求导九 导数及其应用⑴ 函数的单调性4 导数在研究函数中的应用(B)九 导数及其应用⑵ 函数的极值①②存在极值的两个条件求极值的三步骤九 导数及其应用⑶ 函数的最值①②求f(x)在[a,b]上的极值以及f(a),f(b);比较极值与端点值的大小,得出最值。5 导数在实际问题中的应用(B)⑴ 写表达式必带范围⑵ 合理说明最值十 算法初步1 算法的有关概念(A) ⑴ 定义:
对一类问题的机械的、统一的求解方法称为算法
⑵ 两大特点:
有限性 确定性
⑶ 三种基本结构:
顺序结构 选择(条件)结构
循环结构“直到”型循环
特点:先运算后判断
典型例证:吃饭“当”型循环
特点:先判断后运算
典型例证:资格认证十 算法初步十 算法初步2 流程图(A)起止框输入、输出框处理框判断框流程线十 算法初步3 基本算法语句(A)
⑴ 赋值语句;
x 23
⑵ 输入、输出语句;
Read Print 十 算法初步⑶ 条件语句“块”状条件语句
If A then
B……
Else
C……
End if
“行”状条件语句
If A then B……end if 条件语句的嵌套结构
If A then
B
Else if C then
D
Else if E then
F
……
Else
G
End if ⑷ 循环语句十 算法初步For循环 (适用于循环次数确定时)
For I from “初值” to “终值” step “步长”
……
End for
While循环 (循环次数确定不确定都可以使用)
While A
……
End while步长为“1”时可不写⑸ 补充十 算法初步mod (a,b) a除以b的余数
mod(5,2)=?
mod(1,3)=?
1 1
int(x) 不超过x的最大整数
int(1.3)=?
int(-2.7)=?
1 -3十一 常用逻辑用语1 命题的四种形式 (A) 原命题 逆命题 否命题 逆否命题
互为逆否命题的两个命题,要么都是 真命题,要么都是假命题。十一 常用逻辑用语2 充要条件 (B)十一 常用逻辑用语3 简单的逻辑联结词 (A)或 且 非十一 常用逻辑用语4 全称量词与存在量词 (A)十二 推理与证明1 合情推理与演绎推理 (B)十二 推理与证明合情推理与演绎推理的区别:⑴ 特点 ①归纳是由特殊到一般的推理;
②类比是由特殊到特殊的推理;
③演绎推理是由一般到特殊的
推理.
⑵ 从推理的结论来看:
合情推理的结论不一定正确,有待证明;
演绎推理得到的结论一定正确.十二 推理与证明2 分析法与综合法 (A)从已知条件出发,以已知的定义、公理、定理为依据,逐步下推,直到推出要证明的结论为止 综合法从问题的结论出发,追溯导致结论成立的条件,逐步上溯,直到使结论成立的条件和已知条件吻合为止 分析法已知条件结论结论 已知条件 十二 推理与证明3 反证法 (A)反证法是一种常用的间接证明方法. 否定结论 导致矛盾 否定命题不成立 原结论成立 合理的推理 十二 推理与证明反证法的过程包括以下三个步骤:(1) 反设——假设命题的结论不成立,即假定原命题的反面为真;(2) 归谬——从反设和已知条件出发,经过一系列正确的逻辑推理,得出矛盾结果;(3) 存真——由矛盾结果,断定反设不真,从而肯定原结论成立.十三 概率、统计1 抽样方法 (A) ⑴ 简单的随机抽样(特点:总体个数少)
1)抽签法;
2)随机数表法。
⑵ 系统抽样(特点:总体个数多)
⑶ 分层抽样:总体由差异明
显的几个部分组成 十三 概率、统计2 总体分布的估计 (A)⑴ 频率分布表 (频率之和为1)
⑵ 频率分布直方图与折线图
1)纵坐标 频率/组距;
2) 小矩形的面积之和为1。
⑶茎叶图
平均数、众数、中位数十三 概率、统计3 总体特征数的估计 (B)⑴ 平均数
1)公式
2)加权平均十三 概率、统计⑵.稳定程度
极差:Max – Min
方差:
标准差: 十三 概率、统计4 变量的相关性 (A)含义:
能用方程 近似表示的相关关系 。十三 概率、统计5 随机事件与概率 (A)6 古典概型 (B)注:抓住基本事件n,基本事件一般可数十三 概率、统计7 几何概型 (A)“测度”指:长度、面积、体积8 互斥事件及其发生的概率 (A)① 互斥事件② 对立事件不能同时发生的两个事件P(A+B)=P(A)+P(B)两个互斥事件必有一个发生十三 概率、统计注: 题目中出现“至少”,一般用对立事件 9 统计案例 (A)⑴ 独立性检验卡方统计量:其中 n=a+b+c+d 为样本量作为检验在多大程度上可以认为“两个变量有关系”的标准 。十三 概率、统计⑵ 相关性检验 相关系数 r1)计算公式2)相关系数的性质(1)|r|≤1.
(2)|r|越接近于1,相关程度越大;|r|越接近于0,相关程度越小.十四 空间几何体1 柱、锥、台、球及其简单组合体 (A)2 三视图与直观图 (A)注意:三视图的原理十四 空间几何体3 柱、锥、台、球的表面积与体积(A) ⑴ 侧面积十四 空间几何体⑴ 侧面积十四 空间几何体⑴ 侧面积十四 空间几何体⑵ 体积十五 点、线、面之间的位置关系1 平面及其基本性质 (A) ⑴ 异面直线所成角⑵ 线面所成角⑶ 二面角十五 点、线、面之间的位置关系2 直线与平面位置关系 (B)⑴ 直线与平面平行判定定理 如果平面外一条直线和这个平面内的一条直线平行,那么,直线与平面平行.十五 点、线、面之间的位置关系⑴ 直线与平面平行性质定理 如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行.十五 点、线、面之间的位置关系2 直线与平面位置关系 (B)⑵ 直线与平面垂直判定定理 如果一条直线和一个平面内的两条相交直线垂直,那么,这条直线垂直于这个平面.十五 点、线、面之间的位置关系⑵ 直线与平面垂直性质定理 如果两条直线都垂直于同一个平面,那么这两条直线平行.十五 点、线、面之间的位置关系3 平面与平面的位置关系 (B)⑴ 平面与平面平行判定定理 如果一个平面内有两条相交直线都平行于另一个平面,那么,这两个平面平行.十五 点、线、面之间的位置关系⑴ 平面与平面平行性质定理 如果两个平行平面同时和第三个平面相交,那么它们的交线平行.十五 点、线、面之间的位置关系3 平面与平面的位置关系 (B)⑵ 平面与平面垂直判定定理 如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.十五 点、线、面之间的位置关系⑵ 平面与平面垂直性质定理 如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面.十六 平面解析几何初步1 直线的斜率和倾斜角 (B)⑴ 斜率⑵ 倾斜角直线与x轴正半轴所成的角十六 平面解析几何初步2 直线方程 (C)⑴ 点斜式、斜截式点斜式:斜截式:注意1)点斜式、斜截式首先考虑k是否存在;2)斜截式是点斜式的特殊形式;3)若存在k,且过点(a,0),
一般设为 x= my+a.十六 平面解析几何初步⑵ 两点式、截距式两点式:截距式:注意1)两点式中:2)截距式中,注意截距为0的情况;3)截距式是两点式的特殊形式.十六 平面解析几何初步思考十六 平面解析几何初步⑶ 一般式注意可表示平面内任一条直线十六 平面解析几何初步3 直线的平行与垂直关系 (B)⑴ 两条直线平行十六 平面解析几何初步⑵ 两条直线垂直十六 平面解析几何初步⑶ 常用结论十六 平面解析几何初步4 两条直线的交点 (B)联列方程组十六 平面解析几何初步5 两点间距离,点到直线距离 (B)⑴ 两点间距离⑵ 点到直线距离⑶ 两平行直线间距离十六 平面解析几何初步6 圆的标准方程和一般方程 (C)⑴ 标准方程圆心 半径 十六 平面解析几何初步⑵ 一般方程说明: 十六 平面解析几何初步7 直线与圆、圆与圆的位置关系 (B)⑴ 直线与圆的位置关系十六 平面解析几何初步⑵ 圆与圆的位置关系十六 平面解析几何初步8 空间直角坐标系 (A)十七 圆锥曲线与方程1 椭圆 (B)⑴ 定义① 第一定义② 第二定义 到定点F和到定直线L(F不在L上)的
距离之比是一个常数e(0距离之比是一个常数e(e>1).⑵ 双曲线的标准方程与几何性质十七 圆锥曲线与方程3 抛物线 (A)⑴ 定义 到定点F的距离等于到定直线L
(F不在L上)的距离.3 抛物线 (焦点在x轴上)(A)3 抛物线 (焦点在y轴上)(A)
z1+z2=(a+c)+(b+d)i;
z1-z2=(a-c)+(b-d)i.( a + bi )( c + di ) = ( ac – bd ) + ( bc + ad )i.八 复数 2 复数的四则运算(B)⑵ 复数的乘方八 复数 2 复数的四则运算(B)⑶ 共轭复数注:1)当a=0时,共轭复数也称为共轭虚数;
2)实数的共轭复数是它本身。八 复数 2 复数的四则运算(B)⑶ 共轭复数八 复数 2 复数的四则运算(B)⑷ 常用运算性质1)2)八 复数 2 复数的四则运算(B)⑷ 常用运算性质3)八 复数 2 复数的四则运算(B)⑷ 常用运算性质4)八 复数 3 复数的几何意义(A)向量 的模叫做复数z的模,记为则几何意义: 复平面内该点到原点的距离。模的运算性质:模的拓展性质复平面的两点间距离公式①以 对应的点为圆心,r为半径的圆。八 复数 3 复数的几何意义(A)八 复数 3 复数的几何意义(A)②以 对应的点为端点的线段的中垂线;③④以 对应的点为焦点的椭圆;以 对应的点为焦点的双曲线。九 导数及其应用1 导数的概念(A)⑴ 平均变化率⑵ 瞬时变化率——导数①②③曲线上一点处切线的斜率瞬时速度瞬时加速度导数⑶ 求导的一般步骤九 导数及其应用2 导数的几何意义 (B)曲线上一点处切线的斜率3 导数的运算 (B)⑴ 常见函数的导数九 导数及其应用⑵ 导数的运算法则九 导数及其应用⑶ 简单的复合导数求导九 导数及其应用⑴ 函数的单调性4 导数在研究函数中的应用(B)九 导数及其应用⑵ 函数的极值①②存在极值的两个条件求极值的三步骤九 导数及其应用⑶ 函数的最值①②求f(x)在[a,b]上的极值以及f(a),f(b);比较极值与端点值的大小,得出最值。5 导数在实际问题中的应用(B)⑴ 写表达式必带范围⑵ 合理说明最值十 算法初步1 算法的有关概念(A) ⑴ 定义:
对一类问题的机械的、统一的求解方法称为算法
⑵ 两大特点:
有限性 确定性
⑶ 三种基本结构:
顺序结构 选择(条件)结构
循环结构“直到”型循环
特点:先运算后判断
典型例证:吃饭“当”型循环
特点:先判断后运算
典型例证:资格认证十 算法初步十 算法初步2 流程图(A)起止框输入、输出框处理框判断框流程线十 算法初步3 基本算法语句(A)
⑴ 赋值语句;
x 23
⑵ 输入、输出语句;
Read Print 十 算法初步⑶ 条件语句“块”状条件语句
If A then
B……
Else
C……
End if
“行”状条件语句
If A then B……end if 条件语句的嵌套结构
If A then
B
Else if C then
D
Else if E then
F
……
Else
G
End if ⑷ 循环语句十 算法初步For循环 (适用于循环次数确定时)
For I from “初值” to “终值” step “步长”
……
End for
While循环 (循环次数确定不确定都可以使用)
While A
……
End while步长为“1”时可不写⑸ 补充十 算法初步mod (a,b) a除以b的余数
mod(5,2)=?
mod(1,3)=?
1 1
int(x) 不超过x的最大整数
int(1.3)=?
int(-2.7)=?
1 -3十一 常用逻辑用语1 命题的四种形式 (A) 原命题 逆命题 否命题 逆否命题
互为逆否命题的两个命题,要么都是 真命题,要么都是假命题。十一 常用逻辑用语2 充要条件 (B)十一 常用逻辑用语3 简单的逻辑联结词 (A)或 且 非十一 常用逻辑用语4 全称量词与存在量词 (A)十二 推理与证明1 合情推理与演绎推理 (B)十二 推理与证明合情推理与演绎推理的区别:⑴ 特点 ①归纳是由特殊到一般的推理;
②类比是由特殊到特殊的推理;
③演绎推理是由一般到特殊的
推理.
⑵ 从推理的结论来看:
合情推理的结论不一定正确,有待证明;
演绎推理得到的结论一定正确.十二 推理与证明2 分析法与综合法 (A)从已知条件出发,以已知的定义、公理、定理为依据,逐步下推,直到推出要证明的结论为止 综合法从问题的结论出发,追溯导致结论成立的条件,逐步上溯,直到使结论成立的条件和已知条件吻合为止 分析法已知条件结论结论 已知条件 十二 推理与证明3 反证法 (A)反证法是一种常用的间接证明方法. 否定结论 导致矛盾 否定命题不成立 原结论成立 合理的推理 十二 推理与证明反证法的过程包括以下三个步骤:(1) 反设——假设命题的结论不成立,即假定原命题的反面为真;(2) 归谬——从反设和已知条件出发,经过一系列正确的逻辑推理,得出矛盾结果;(3) 存真——由矛盾结果,断定反设不真,从而肯定原结论成立.十三 概率、统计1 抽样方法 (A) ⑴ 简单的随机抽样(特点:总体个数少)
1)抽签法;
2)随机数表法。
⑵ 系统抽样(特点:总体个数多)
⑶ 分层抽样:总体由差异明
显的几个部分组成 十三 概率、统计2 总体分布的估计 (A)⑴ 频率分布表 (频率之和为1)
⑵ 频率分布直方图与折线图
1)纵坐标 频率/组距;
2) 小矩形的面积之和为1。
⑶茎叶图
平均数、众数、中位数十三 概率、统计3 总体特征数的估计 (B)⑴ 平均数
1)公式
2)加权平均十三 概率、统计⑵.稳定程度
极差:Max – Min
方差:
标准差: 十三 概率、统计4 变量的相关性 (A)含义:
能用方程 近似表示的相关关系 。十三 概率、统计5 随机事件与概率 (A)6 古典概型 (B)注:抓住基本事件n,基本事件一般可数十三 概率、统计7 几何概型 (A)“测度”指:长度、面积、体积8 互斥事件及其发生的概率 (A)① 互斥事件② 对立事件不能同时发生的两个事件P(A+B)=P(A)+P(B)两个互斥事件必有一个发生十三 概率、统计注: 题目中出现“至少”,一般用对立事件 9 统计案例 (A)⑴ 独立性检验卡方统计量:其中 n=a+b+c+d 为样本量作为检验在多大程度上可以认为“两个变量有关系”的标准 。十三 概率、统计⑵ 相关性检验 相关系数 r1)计算公式2)相关系数的性质(1)|r|≤1.
(2)|r|越接近于1,相关程度越大;|r|越接近于0,相关程度越小.十四 空间几何体1 柱、锥、台、球及其简单组合体 (A)2 三视图与直观图 (A)注意:三视图的原理十四 空间几何体3 柱、锥、台、球的表面积与体积(A) ⑴ 侧面积十四 空间几何体⑴ 侧面积十四 空间几何体⑴ 侧面积十四 空间几何体⑵ 体积十五 点、线、面之间的位置关系1 平面及其基本性质 (A) ⑴ 异面直线所成角⑵ 线面所成角⑶ 二面角十五 点、线、面之间的位置关系2 直线与平面位置关系 (B)⑴ 直线与平面平行判定定理 如果平面外一条直线和这个平面内的一条直线平行,那么,直线与平面平行.十五 点、线、面之间的位置关系⑴ 直线与平面平行性质定理 如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行.十五 点、线、面之间的位置关系2 直线与平面位置关系 (B)⑵ 直线与平面垂直判定定理 如果一条直线和一个平面内的两条相交直线垂直,那么,这条直线垂直于这个平面.十五 点、线、面之间的位置关系⑵ 直线与平面垂直性质定理 如果两条直线都垂直于同一个平面,那么这两条直线平行.十五 点、线、面之间的位置关系3 平面与平面的位置关系 (B)⑴ 平面与平面平行判定定理 如果一个平面内有两条相交直线都平行于另一个平面,那么,这两个平面平行.十五 点、线、面之间的位置关系⑴ 平面与平面平行性质定理 如果两个平行平面同时和第三个平面相交,那么它们的交线平行.十五 点、线、面之间的位置关系3 平面与平面的位置关系 (B)⑵ 平面与平面垂直判定定理 如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.十五 点、线、面之间的位置关系⑵ 平面与平面垂直性质定理 如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面.十六 平面解析几何初步1 直线的斜率和倾斜角 (B)⑴ 斜率⑵ 倾斜角直线与x轴正半轴所成的角十六 平面解析几何初步2 直线方程 (C)⑴ 点斜式、斜截式点斜式:斜截式:注意1)点斜式、斜截式首先考虑k是否存在;2)斜截式是点斜式的特殊形式;3)若存在k,且过点(a,0),
一般设为 x= my+a.十六 平面解析几何初步⑵ 两点式、截距式两点式:截距式:注意1)两点式中:2)截距式中,注意截距为0的情况;3)截距式是两点式的特殊形式.十六 平面解析几何初步思考十六 平面解析几何初步⑶ 一般式注意可表示平面内任一条直线十六 平面解析几何初步3 直线的平行与垂直关系 (B)⑴ 两条直线平行十六 平面解析几何初步⑵ 两条直线垂直十六 平面解析几何初步⑶ 常用结论十六 平面解析几何初步4 两条直线的交点 (B)联列方程组十六 平面解析几何初步5 两点间距离,点到直线距离 (B)⑴ 两点间距离⑵ 点到直线距离⑶ 两平行直线间距离十六 平面解析几何初步6 圆的标准方程和一般方程 (C)⑴ 标准方程圆心 半径 十六 平面解析几何初步⑵ 一般方程说明: 十六 平面解析几何初步7 直线与圆、圆与圆的位置关系 (B)⑴ 直线与圆的位置关系十六 平面解析几何初步⑵ 圆与圆的位置关系十六 平面解析几何初步8 空间直角坐标系 (A)十七 圆锥曲线与方程1 椭圆 (B)⑴ 定义① 第一定义② 第二定义 到定点F和到定直线L(F不在L上)的
距离之比是一个常数e(0
(F不在L上)的距离.3 抛物线 (焦点在x轴上)(A)3 抛物线 (焦点在y轴上)(A)
同课章节目录
