2023-2024学年北京八中初三第二学期开学数学练习 (PDF版,无答案)
文档属性
| 名称 | 2023-2024学年北京八中初三第二学期开学数学练习 (PDF版,无答案) |  | |
| 格式 | |||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-11 14:29:14 | ||
图片预览



文档简介
北京八中2023-2024学年初三第二学期开学练习
开学练习
班级_____________姓名______________学号______________
一、选择题(共 16分,每题 2分)
第 1-8题均有四个选项,符合题意的选项只有一个.
从正面看
1.右图是一个拱形积木玩具,其主视图是
(A) (B) (C) (D)
2.2022年北京打造了一届绿色环保的冬奥会.张家口赛区按照“渗、滞、蓄、净、用、排”
的原则,在古杨树场馆群修建了 250000立方米雨水收集池,用于收集雨水和融雪水,最
大限度减少水资源浪费.将 250000用科学记数法表示应为
(A) (B) (C) (D)
3.如图, , , 平分 ,则
的大小为
(A) (B)
(C) (D)
4.若一个多边形的每个外角都是 30°,则这个多边形的边数为
(A)6 (B)8 (C)10 (D)12
5.不透明的袋子中装有 2个红球,3个黑球,这些球除颜色外无其他差别.从袋子中随机摸出
一个球,则摸出红球的概率是
(A) (B) (C) (D)
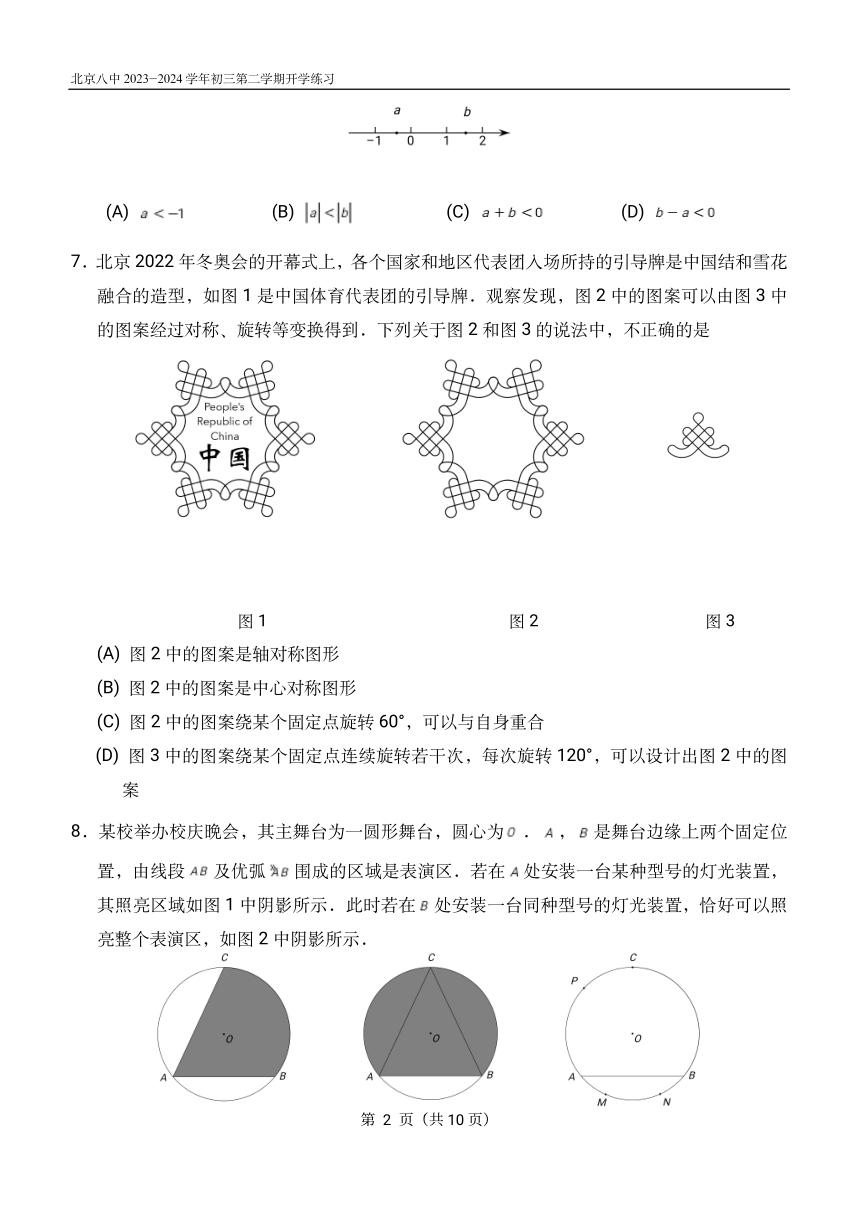
6.实数 , 在数轴上的对应点的位置如图所示,下列结论中正确的是
第 1页(共 10页)
北京八中2023-2024学年初三第二学期开学练习
(A) (B) (C) (D)
7.北京 2022年冬奥会的开幕式上,各个国家和地区代表团入场所持的引导牌是中国结和雪花
融合的造型,如图 1是中国体育代表团的引导牌.观察发现,图 2中的图案可以由图 3中
的图案经过对称、旋转等变换得到.下列关于图 2和图 3的说法中,不正确的是
图 1 图 2 图 3
(A)图 2中的图案是轴对称图形
(B)图 2中的图案是中心对称图形
(C)图 2中的图案绕某个固定点旋转 60°,可以与自身重合
(D)图 3中的图案绕某个固定点连续旋转若干次,每次旋转 120°,可以设计出图 2中的图
案
8.某校举办校庆晚会,其主舞台为一圆形舞台,圆心为 . , 是舞台边缘上两个固定位
置,由线段 及优弧 围成的区域是表演区.若在 处安装一台某种型号的灯光装置,
其照亮区域如图 1中阴影所示.此时若在 处安装一台同种型号的灯光装置,恰好可以照
亮整个表演区,如图 2中阴影所示.
第 2页(共 10页)
北京八中2023-2024学年初三第二学期开学练习
图 1 图 2 图 3
若将灯光装置改放在如图 3所示的点 , 或 处,能使表演区完全照亮的方案可能是
①在 处放置 2台该型号灯光装置
②在 , 处各放置 1台该型号灯光装置
③在 处放置 2台该型号灯光装置
(A)①② (B)①③ (C)②③ (D)①②③
二、填空题(共 16分,每题 2分)
9.若代数式 有意义,则实数 x的取值范围是 .
10.已知 ,且 m是整数,请写出一个符合要求的 m的值 .
11.分解因式: .
12.如图,PA,PB是⊙O的切线,A,B为切点.若∠APB=60°,
则∠AOP的大小为 .
13.已知关于 x的一元二次方程 没有实数根,则 m的取值
范围是 .
14.在平面直角坐标系 xOy中,直线 与双曲线 交于点 和点 ,则点 B的
坐标为__________.
15.如图,在 4×4的正方形网格中,A,B,C,D,E是网格线交点,请画出
一个△DEF,且 F是网格线交点,使得△DEF与△ABC全等.
16.某企业有 A,B两条加工相同原材料的生产线,在一天内,A生产线共加
工 a吨原材料,加工时间为(4a+1)小时;在一天内,B生产线共加工 b吨原材料,加工时
间为(2b+3)小时,第一天,该企业将 5吨原材料分配到 A,B两条生产线,两条生产线都
在一天内完成了加工,且加工时间相同,则分配到 A生产线的吨数与分配到 B生产线的吨
数的比为_________.第二天开工前,该企业按第一天的分配结果分配了 5吨原材料后,又给
A生产线分配了 m吨原材料,给 B生产线分配了 n吨原材料若两条生产线都能在一天内加
第 3页(共 10页)
北京八中2023-2024学年初三第二学期开学练习
工完各自分配到的所有原材料,且加工时间相同,则 的值为_________.三、解答题(共
68分,第 17-20题,每题 5分,第 21题 6分,第 22题 5分,第 23-24题,每题 6分,
第 25题 5分,第 26题 6分,第 27-28题,每题 7分)
解答应写出文字说明、演算步骤或证明过程.
17.计算:
18.解不等式组:
19.已知 ,求代数式 的值.
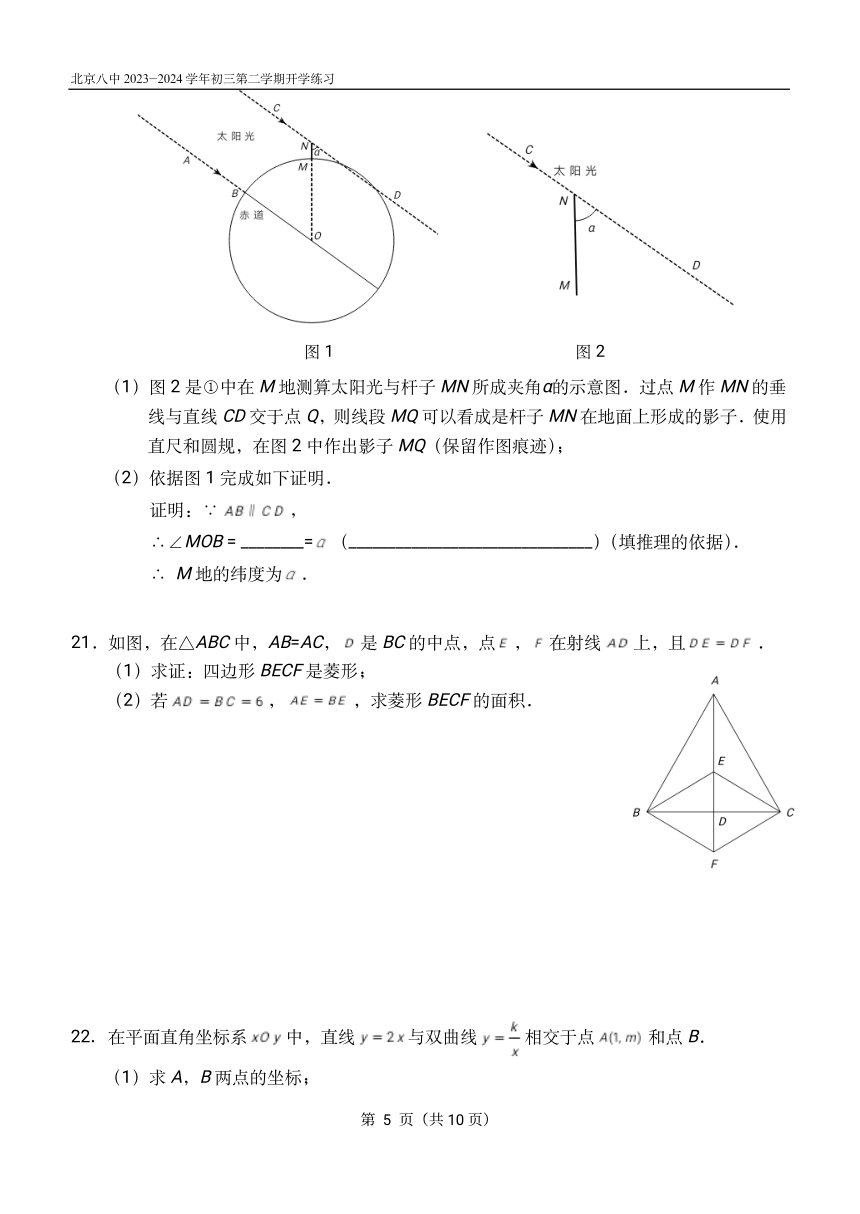
20.《元史·天文志》中记载了元朝著名天文学家郭守敬主持的一次大规模观测,称为“四海
测验”.这次观测主要使用了“立杆测影”的方法,在二十七个观测点测量出的各地的“北
极出地”与现在人们所说的“北纬”完全吻合.利用类似的原理,我们也可以测量出所在
地的纬度.如图 1所示.
①春分时,太阳光直射赤道.此时在 M地直立一根杆子 MN,在太阳光照射下,杆子 MN
会在地面上形成影子.通过测量杆子的长度与它的影子的长度,可以计算出太阳光与杆
子 MN所成的夹角α;
②由于同一时刻的太阳光线可以近似看成是平行的,所以根据太阳光与杆子 MN所成的夹
角α可以测算得到 M地的纬度,即∠MOB的大小.
第 4页(共 10页)
北京八中2023-2024学年初三第二学期开学练习
图 1 图 2
(1)图 2是①中在 M地测算太阳光与杆子 MN所成夹角α的示意图.过点 M作 MN的垂
线与直线 CD交于点 Q,则线段 MQ可以看成是杆子 MN在地面上形成的影子.使用
直尺和圆规,在图 2中作出影子 MQ(保留作图痕迹);
(2)依据图 1完成如下证明.
证明:∵ ,
∴∠MOB=________= (_______________________________)(填推理的依据).
∴ M地的纬度为 .
21.如图,在△ABC中,AB=AC, 是 BC的中点,点 , 在射线 上,且 .
(1)求证:四边形 BECF是菱形;
(2)若 , ,求菱形 BECF的面积.
22.在平面直角坐标系 中,直线 与双曲线 相交于点 和点 B.
(1)求 A,B两点的坐标;
第 5页(共 10页)
北京八中2023-2024学年初三第二学期开学练习
(2)已知点 ,过点 C作平行于 y轴的直线,与直线 与双曲线 的交点分
别为点 和点 .当 时,直接写出 n的取值范围
23.要修建一个圆形喷水池,在池中心竖直安装一根水管,水管的顶端安一个喷水头,记喷出
的水与池中心的水平距离为 xm,距地面的高度为 ym.测量得到如下数值:
x/m 0 0.5 1 1.5 2 2.5 3 3.37
y/m 2.44 3.15 3.49 3.45 3.04 2.25 1.09 0
小腾根据学习函数的经验,发现 y是 x的函数,并对 y随 x的变化而变化的规律进行了探究.
下面是小腾的探究过程,请补充完整:
(1) 在平面直角坐标系 xOy中,描出表中各组数值所对应的点(x,y),并画出函数的
图象;
(2)结合函数图象,出水口距地面的高度为_______m,水达到最高点时与池中心的水平
距离约为_______m(结果保留小数点后两位);
(3)为了使水柱落地点与池中心的距离不超过 3.2m,如果只调整水管的高度,其他条件
不变,结合函数图象,估计出水口至少需要_______(填“升高”或“降低”)_______m
(结果保留小数点后两位).
24.如图,⊙O是 Rt△ABC的外接圆,AB是⊙O的直径,点 D为 的中点,⊙O的切线 DE
交 OC的延长线于点 E.
第 6页(共 10页)
北京八中2023-2024学年初三第二学期开学练习
(1)求证:DE∥AC;
(2)连接 BD交 AC于 P,若 AC=8, ,
求 DE和 BP的长.
25.为增进学生对营养与健康知识的了解,某校开展了两次知识问答活动,从中随机抽取了 20
名学生两次活动的成绩(百分制),并对数据(成绩)进行整理、描述和分析.下图是这
20名学生第一次活动和第二次活动成绩情况统计图.
(1)①学生甲第一次成绩是 85分,则该生第二次成绩是_______分,他两次活动的平均成
绩是_______分;
②学生乙第一次成绩低于 80分,第二次成绩高于 90分,请在图中用“〇”圈出代表
乙的点;
(2)为了解每位学生两次活动平均成绩的情况,A,B,C三人分别作出了每位学生两次
活动平均成绩的频数分布直方图(数据分成6组: , , ,
, , ):
第 7页(共 10页)
北京八中2023-2024学年初三第二学期开学练习
A B C
已知这三人中只有一人正确作出了统计图,则作图正确的是_______;
(3)假设有 400名学生参加此次活动,估计两次活动平均成绩不低于 90分的学生人数为
___________.
第 8页(共 10页)
北京八中2023-2024学年初三第二学期开学练习
26.在平面直角坐标系 中,点 ( , ),点 (, )在抛物线 ( )
上.设抛物线的对称轴为 .
(1)当 时,
①直接写出 与 满足的等量关系;
②比较 , 的大小,并说明理由;
(2)已知点 ( , )在该抛物线上,若对于 时,都有 ,求 的取值范
围.
第 9页(共 10页)
北京八中2023-2024学年初三第二学期开学练习
27.如图,∠MON=α,点 A在 ON上,过点 A作 OM的平行线,与∠MON的平分线交于点 B,
点 C在 OB上(不与点 O,B重合),连接 AC,将线段 AC绕点 A顺时针旋转 180°-α,得
到线段 AD,连接 BD.
(1)直接写出线段 AO与 AB之间的数量关系,并证明∠MOB=∠DBA;
(2)连接 DC并延长,分别交 AB,OM于点 E,F.若α=60°,用等式表示线段 EF与 AC之
间的数量关系,并证明.
第 10页(共 10页)
北京八中2023-2024学年初三第二学期开学练习
28.在平面直角坐标系 中,对于点 ,给出如下定义:当点 满足
时,称点 是点 的等和点.
已知,点 .
(1)如图 1,在 , , 中,点 的等和点有________;
(2)点 在直线 上,若点 的等和点也是点 的等和点,求点 的坐标;
(3)已知点 B(b,0)和线段 MN,对于所有满足 BC=1的点 C,线段 MN上总存在线段
PC上每个点的等和点.若 MN的最小值为 5,直接写出 b的取值范围.
第 11页(共 10页)
开学练习
班级_____________姓名______________学号______________
一、选择题(共 16分,每题 2分)
第 1-8题均有四个选项,符合题意的选项只有一个.
从正面看
1.右图是一个拱形积木玩具,其主视图是
(A) (B) (C) (D)
2.2022年北京打造了一届绿色环保的冬奥会.张家口赛区按照“渗、滞、蓄、净、用、排”
的原则,在古杨树场馆群修建了 250000立方米雨水收集池,用于收集雨水和融雪水,最
大限度减少水资源浪费.将 250000用科学记数法表示应为
(A) (B) (C) (D)
3.如图, , , 平分 ,则
的大小为
(A) (B)
(C) (D)
4.若一个多边形的每个外角都是 30°,则这个多边形的边数为
(A)6 (B)8 (C)10 (D)12
5.不透明的袋子中装有 2个红球,3个黑球,这些球除颜色外无其他差别.从袋子中随机摸出
一个球,则摸出红球的概率是
(A) (B) (C) (D)
6.实数 , 在数轴上的对应点的位置如图所示,下列结论中正确的是
第 1页(共 10页)
北京八中2023-2024学年初三第二学期开学练习
(A) (B) (C) (D)
7.北京 2022年冬奥会的开幕式上,各个国家和地区代表团入场所持的引导牌是中国结和雪花
融合的造型,如图 1是中国体育代表团的引导牌.观察发现,图 2中的图案可以由图 3中
的图案经过对称、旋转等变换得到.下列关于图 2和图 3的说法中,不正确的是
图 1 图 2 图 3
(A)图 2中的图案是轴对称图形
(B)图 2中的图案是中心对称图形
(C)图 2中的图案绕某个固定点旋转 60°,可以与自身重合
(D)图 3中的图案绕某个固定点连续旋转若干次,每次旋转 120°,可以设计出图 2中的图
案
8.某校举办校庆晚会,其主舞台为一圆形舞台,圆心为 . , 是舞台边缘上两个固定位
置,由线段 及优弧 围成的区域是表演区.若在 处安装一台某种型号的灯光装置,
其照亮区域如图 1中阴影所示.此时若在 处安装一台同种型号的灯光装置,恰好可以照
亮整个表演区,如图 2中阴影所示.
第 2页(共 10页)
北京八中2023-2024学年初三第二学期开学练习
图 1 图 2 图 3
若将灯光装置改放在如图 3所示的点 , 或 处,能使表演区完全照亮的方案可能是
①在 处放置 2台该型号灯光装置
②在 , 处各放置 1台该型号灯光装置
③在 处放置 2台该型号灯光装置
(A)①② (B)①③ (C)②③ (D)①②③
二、填空题(共 16分,每题 2分)
9.若代数式 有意义,则实数 x的取值范围是 .
10.已知 ,且 m是整数,请写出一个符合要求的 m的值 .
11.分解因式: .
12.如图,PA,PB是⊙O的切线,A,B为切点.若∠APB=60°,
则∠AOP的大小为 .
13.已知关于 x的一元二次方程 没有实数根,则 m的取值
范围是 .
14.在平面直角坐标系 xOy中,直线 与双曲线 交于点 和点 ,则点 B的
坐标为__________.
15.如图,在 4×4的正方形网格中,A,B,C,D,E是网格线交点,请画出
一个△DEF,且 F是网格线交点,使得△DEF与△ABC全等.
16.某企业有 A,B两条加工相同原材料的生产线,在一天内,A生产线共加
工 a吨原材料,加工时间为(4a+1)小时;在一天内,B生产线共加工 b吨原材料,加工时
间为(2b+3)小时,第一天,该企业将 5吨原材料分配到 A,B两条生产线,两条生产线都
在一天内完成了加工,且加工时间相同,则分配到 A生产线的吨数与分配到 B生产线的吨
数的比为_________.第二天开工前,该企业按第一天的分配结果分配了 5吨原材料后,又给
A生产线分配了 m吨原材料,给 B生产线分配了 n吨原材料若两条生产线都能在一天内加
第 3页(共 10页)
北京八中2023-2024学年初三第二学期开学练习
工完各自分配到的所有原材料,且加工时间相同,则 的值为_________.三、解答题(共
68分,第 17-20题,每题 5分,第 21题 6分,第 22题 5分,第 23-24题,每题 6分,
第 25题 5分,第 26题 6分,第 27-28题,每题 7分)
解答应写出文字说明、演算步骤或证明过程.
17.计算:
18.解不等式组:
19.已知 ,求代数式 的值.
20.《元史·天文志》中记载了元朝著名天文学家郭守敬主持的一次大规模观测,称为“四海
测验”.这次观测主要使用了“立杆测影”的方法,在二十七个观测点测量出的各地的“北
极出地”与现在人们所说的“北纬”完全吻合.利用类似的原理,我们也可以测量出所在
地的纬度.如图 1所示.
①春分时,太阳光直射赤道.此时在 M地直立一根杆子 MN,在太阳光照射下,杆子 MN
会在地面上形成影子.通过测量杆子的长度与它的影子的长度,可以计算出太阳光与杆
子 MN所成的夹角α;
②由于同一时刻的太阳光线可以近似看成是平行的,所以根据太阳光与杆子 MN所成的夹
角α可以测算得到 M地的纬度,即∠MOB的大小.
第 4页(共 10页)
北京八中2023-2024学年初三第二学期开学练习
图 1 图 2
(1)图 2是①中在 M地测算太阳光与杆子 MN所成夹角α的示意图.过点 M作 MN的垂
线与直线 CD交于点 Q,则线段 MQ可以看成是杆子 MN在地面上形成的影子.使用
直尺和圆规,在图 2中作出影子 MQ(保留作图痕迹);
(2)依据图 1完成如下证明.
证明:∵ ,
∴∠MOB=________= (_______________________________)(填推理的依据).
∴ M地的纬度为 .
21.如图,在△ABC中,AB=AC, 是 BC的中点,点 , 在射线 上,且 .
(1)求证:四边形 BECF是菱形;
(2)若 , ,求菱形 BECF的面积.
22.在平面直角坐标系 中,直线 与双曲线 相交于点 和点 B.
(1)求 A,B两点的坐标;
第 5页(共 10页)
北京八中2023-2024学年初三第二学期开学练习
(2)已知点 ,过点 C作平行于 y轴的直线,与直线 与双曲线 的交点分
别为点 和点 .当 时,直接写出 n的取值范围
23.要修建一个圆形喷水池,在池中心竖直安装一根水管,水管的顶端安一个喷水头,记喷出
的水与池中心的水平距离为 xm,距地面的高度为 ym.测量得到如下数值:
x/m 0 0.5 1 1.5 2 2.5 3 3.37
y/m 2.44 3.15 3.49 3.45 3.04 2.25 1.09 0
小腾根据学习函数的经验,发现 y是 x的函数,并对 y随 x的变化而变化的规律进行了探究.
下面是小腾的探究过程,请补充完整:
(1) 在平面直角坐标系 xOy中,描出表中各组数值所对应的点(x,y),并画出函数的
图象;
(2)结合函数图象,出水口距地面的高度为_______m,水达到最高点时与池中心的水平
距离约为_______m(结果保留小数点后两位);
(3)为了使水柱落地点与池中心的距离不超过 3.2m,如果只调整水管的高度,其他条件
不变,结合函数图象,估计出水口至少需要_______(填“升高”或“降低”)_______m
(结果保留小数点后两位).
24.如图,⊙O是 Rt△ABC的外接圆,AB是⊙O的直径,点 D为 的中点,⊙O的切线 DE
交 OC的延长线于点 E.
第 6页(共 10页)
北京八中2023-2024学年初三第二学期开学练习
(1)求证:DE∥AC;
(2)连接 BD交 AC于 P,若 AC=8, ,
求 DE和 BP的长.
25.为增进学生对营养与健康知识的了解,某校开展了两次知识问答活动,从中随机抽取了 20
名学生两次活动的成绩(百分制),并对数据(成绩)进行整理、描述和分析.下图是这
20名学生第一次活动和第二次活动成绩情况统计图.
(1)①学生甲第一次成绩是 85分,则该生第二次成绩是_______分,他两次活动的平均成
绩是_______分;
②学生乙第一次成绩低于 80分,第二次成绩高于 90分,请在图中用“〇”圈出代表
乙的点;
(2)为了解每位学生两次活动平均成绩的情况,A,B,C三人分别作出了每位学生两次
活动平均成绩的频数分布直方图(数据分成6组: , , ,
, , ):
第 7页(共 10页)
北京八中2023-2024学年初三第二学期开学练习
A B C
已知这三人中只有一人正确作出了统计图,则作图正确的是_______;
(3)假设有 400名学生参加此次活动,估计两次活动平均成绩不低于 90分的学生人数为
___________.
第 8页(共 10页)
北京八中2023-2024学年初三第二学期开学练习
26.在平面直角坐标系 中,点 ( , ),点 (, )在抛物线 ( )
上.设抛物线的对称轴为 .
(1)当 时,
①直接写出 与 满足的等量关系;
②比较 , 的大小,并说明理由;
(2)已知点 ( , )在该抛物线上,若对于 时,都有 ,求 的取值范
围.
第 9页(共 10页)
北京八中2023-2024学年初三第二学期开学练习
27.如图,∠MON=α,点 A在 ON上,过点 A作 OM的平行线,与∠MON的平分线交于点 B,
点 C在 OB上(不与点 O,B重合),连接 AC,将线段 AC绕点 A顺时针旋转 180°-α,得
到线段 AD,连接 BD.
(1)直接写出线段 AO与 AB之间的数量关系,并证明∠MOB=∠DBA;
(2)连接 DC并延长,分别交 AB,OM于点 E,F.若α=60°,用等式表示线段 EF与 AC之
间的数量关系,并证明.
第 10页(共 10页)
北京八中2023-2024学年初三第二学期开学练习
28.在平面直角坐标系 中,对于点 ,给出如下定义:当点 满足
时,称点 是点 的等和点.
已知,点 .
(1)如图 1,在 , , 中,点 的等和点有________;
(2)点 在直线 上,若点 的等和点也是点 的等和点,求点 的坐标;
(3)已知点 B(b,0)和线段 MN,对于所有满足 BC=1的点 C,线段 MN上总存在线段
PC上每个点的等和点.若 MN的最小值为 5,直接写出 b的取值范围.
第 11页(共 10页)
同课章节目录
