冀教版数学七上2.4《线段的和与差》word学案(无答案)
文档属性
| 名称 | 冀教版数学七上2.4《线段的和与差》word学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 38.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-31 22:00:38 | ||
图片预览

文档简介
冀教版七年级上册----2.4线段的和与差 导学案
单位:蔡园中学 编者:韩秀艳 审核领导:晏志桓 日期:2013、12
课题:2.4 线段的和与差
学习目标 结合图形理解线段的和差倍分,能进行正确的运算,并会相应的作图。培养学生的作图能力和几何推理能力。结合图形理解线段中点及线段的三等分点等的概念,会用几何语言表示,并能进行相应的推理计算。
重点难点 1.能运用线段的中点及和差倍分进行正确的推理计算;并能进行相应的作图。2.规范学生的解题格式。
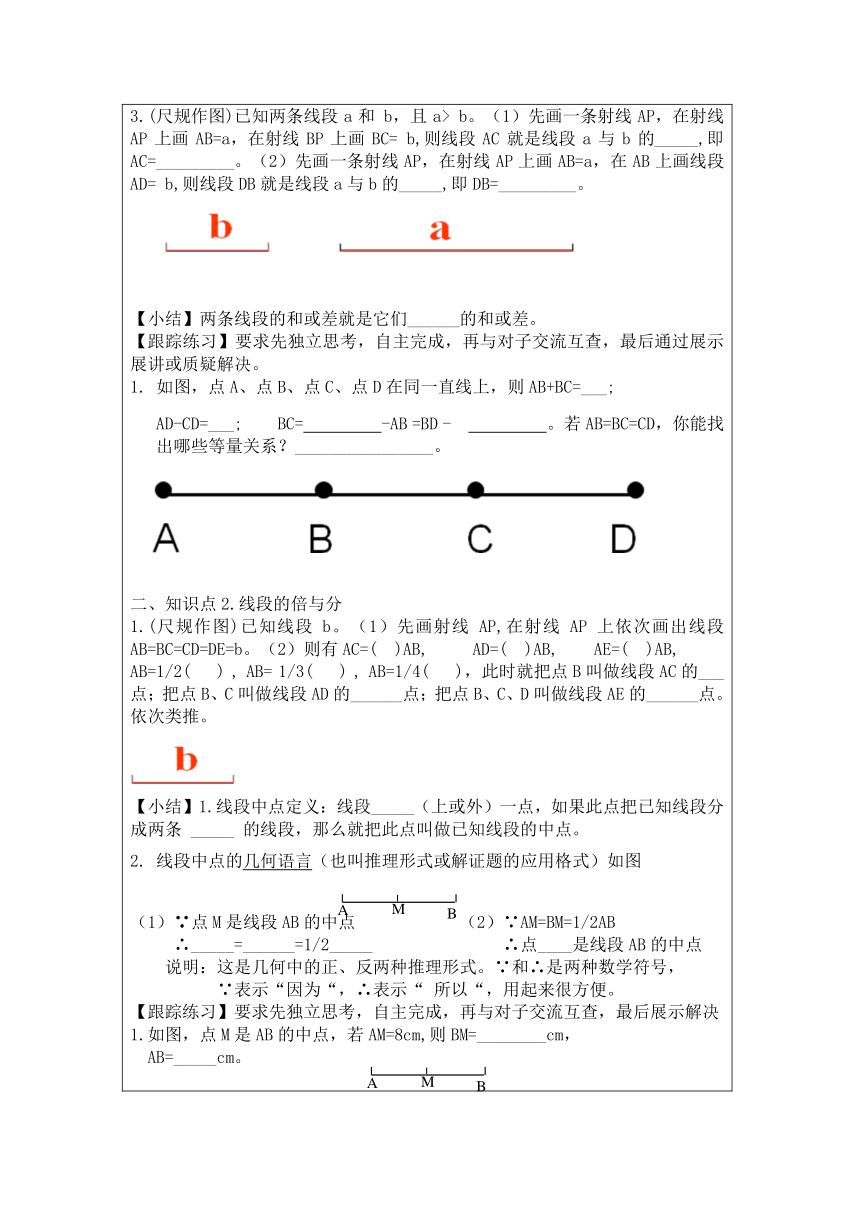
【复习案】【学法指导】独立思考,自主完成,回忆作一条线段等于已知线段的尺规作图方法;尺规作图:作一条线段等于已知线段已知:如图线段b 求作:AB=b作法:①作射线AP ②用圆规量取b ③以A为圆心,b为半径画弧,交射线AP于B点。 所以,AB= b为所求。 注意:尺规作图保留作图痕迹。2.已知等式8=8,则8+5=8+5, ( http: / / www.21cnjy.com )8-5=8-5,因此可知:在等式两边分别____或____相等的量,等式仍然成立。这就是今后我们要学习的等式的性质。【自学案】【学法指导】第一步:要求先读题,自己分析,作图,最后通过观察猜结论; 第二步:与对子交流、讨论、互查; 第三步:总结概括知识点一、知识点1.线段的和与差1.画线段AB=1cm,延长AB到C,使BC=1.5cm。请猜想:线段AC和AB、BC之间数量关系为________________。2.画线段MN=3cm,在MN上截取线段MP=2cm。请猜想:线段PN和MN、MP之间数量关系为________________。3.(尺规作图)已知两条线段a和 b,且a ( http: / / www.21cnjy.com )> b。(1)先画一条射线AP,在射线AP上画AB=a,在射线BP上画BC= b,则线段AC就是线段a与b的 _____,即AC=_________。(2)先画一条射线AP,在射线AP上画AB=a,在AB上画线段AD= b,则线段DB就是线段a与b的 _____,即DB=_________。 【小结】两条线段的和或差就是它们______的和或差。【跟踪练习】要求先独立思考,自主完成,再与对子交流互查,最后通过展示展讲或质疑解决。如图,点A、点B、点C、点D在同一直线上,则AB+BC=___; AD-CD=___; BC= -AB =BD - 。若AB=BC=CD,你能找出哪些等量关系?________________。 ( http: / / www.21cnjy.com )二、知识点2.线段的倍与分1.(尺规作图)已知线段b ( http: / / www.21cnjy.com )。(1)先画射线AP,在射线AP上依次画出线段AB=BC=CD=DE=b。(2)则有AC=( )AB, AD=( )AB, AE=( )AB,AB=1/2( ) , AB= 1 ( http: / / www.21cnjy.com )/3( ) , AB=1/4( ),此时就把点B叫做线段AC的___点;把点B、C叫做线段AD的______点;把点B、C、D叫做线段AE的______点。依次类推。 【小结】1.线段中点定义:线段_____(上或外)一点,如果此点把已知线段分成两条 _____ 的线段,那么就把此点叫做已知线段的中点。线段中点的几何语言(也叫推理形式或解证题的应用格式)如图(1)∵点M是线段AB的中点 (2)∵AM=BM=1/2AB ∴_____=______=1/2_____ ∴点____是线段AB的中点 说明:这是几何中的正、反两种推理形式。∵和∴是两种数学符号, ∵表示“因为“,∴表示“ 所以“,用起来很方便。【跟踪练习】要求先独立思考,自主完成,再与对子交流互查,最后展示解决1.如图,点M是AB的中点,若AM=8cm,则BM=________cm,AB=_____cm。 2.如图,已知点C是线段AB的中点,点D是线段AC的中点,(1)AB= BC (2)BC= AD (3)BD=_____AD 三、自学课本73页的例1、例2,然后回答:1.例1____(是或不是)尺规作图,理由是_________。应注意画图后应写_______。2.通过例2可以感知几何解题说理过程的书写方法为:从______出发,运用所学定义、性质等进行合理推理。【探究案】【学法指导】第一步:独立思考,写出答案 第二步:与对子、小组交流、讨论、互查; 第三步:通过展示展讲,师生点评; 第四步:总结解题思想方法;温馨提示:做题时可以画草图解答,请画在该题附近。点A、B、C都是直线h上的点,且点 ( http: / / www.21cnjy.com )B、C依次在点A的同侧,AB=6 cm,BC=4cm, O是AC的中点,则O、B两点间的距离是______ cm。在直线h上取A、B、C三点,使得AB=6 cm,BC=4 cm。如果O是线段AC的中点,则OB=_____ cm。【小结】第2题运用的数学思想方法是____________。【训练案】题组一1.已知AB=5 cm,延长AB到C,使BC=2.4 cm,在找出AC的中点O,则CO= ____ cm,OB=____ cm。2. 如图,B、C为线段AD上的两点,点C为线段AD的中点AC=5cm,BD=6cm,则线段AB=____ cm。3.在直线h上取M、N、O三点,使得MN=10cm,NO=8cm。如果P是线段MO的中点,则PN=_____ cm。题组二 1.如图AD=7cm,CB=7cm。AC与DB相等吗?请说明理由。 解(1)__________。 ∵AD=7, CB=7 (已知) ∴___=___ (等量代换) ∴AD-___=CB-___ (等式的性质) ∴AC=BD 【总结与反思】【学法指导】可以总结本节课的重点内容,也可以使自己总结的方法、易错点、感受。____________________________________________________________________________________________________【检测案】【学习要求】根据自己的能力选择测试题,1、2、3为必做题,4为选作题。已知如图,点C是线段AB的中点,AB=4cm,BD=1cm,则CD的长度为_____ cm。2. 在一条直线上取D、E、F三点,使DE=5cm,EF=2cm,并且取线段DF的中点O,则线段OE=______ cm。3.如图,已知线段a和 b。(要求:尺规作图) 画线段EF,使EF=a+2b画线段PH,使PH=3b-a 4. 点P是线段MN上一点,点Q是NP的中点,MQ=6,则MP+MN=__布置作业:必做题 1. 课本74页A组第3题。2.如图AC=BD,M是CD的中点,那么M是AB的中点吗?请说明理由。 解:M___AB的中点。 ∵M是CD的中点(已知) ∴___=___ (中点定义)∵AC=BD (已知) ∴AC+CM=BD+DM ( ) ∴___=____ ∴M___AB的中点 (中点定义)选做题 课本74页B组第2题。
A
B
M
A
B
M
B
C
D
A
D
C
B
A
D
C
B
A
C
D
B
A
b
a
M
D
C
B
A
单位:蔡园中学 编者:韩秀艳 审核领导:晏志桓 日期:2013、12
课题:2.4 线段的和与差
学习目标 结合图形理解线段的和差倍分,能进行正确的运算,并会相应的作图。培养学生的作图能力和几何推理能力。结合图形理解线段中点及线段的三等分点等的概念,会用几何语言表示,并能进行相应的推理计算。
重点难点 1.能运用线段的中点及和差倍分进行正确的推理计算;并能进行相应的作图。2.规范学生的解题格式。
【复习案】【学法指导】独立思考,自主完成,回忆作一条线段等于已知线段的尺规作图方法;尺规作图:作一条线段等于已知线段已知:如图线段b 求作:AB=b作法:①作射线AP ②用圆规量取b ③以A为圆心,b为半径画弧,交射线AP于B点。 所以,AB= b为所求。 注意:尺规作图保留作图痕迹。2.已知等式8=8,则8+5=8+5, ( http: / / www.21cnjy.com )8-5=8-5,因此可知:在等式两边分别____或____相等的量,等式仍然成立。这就是今后我们要学习的等式的性质。【自学案】【学法指导】第一步:要求先读题,自己分析,作图,最后通过观察猜结论; 第二步:与对子交流、讨论、互查; 第三步:总结概括知识点一、知识点1.线段的和与差1.画线段AB=1cm,延长AB到C,使BC=1.5cm。请猜想:线段AC和AB、BC之间数量关系为________________。2.画线段MN=3cm,在MN上截取线段MP=2cm。请猜想:线段PN和MN、MP之间数量关系为________________。3.(尺规作图)已知两条线段a和 b,且a ( http: / / www.21cnjy.com )> b。(1)先画一条射线AP,在射线AP上画AB=a,在射线BP上画BC= b,则线段AC就是线段a与b的 _____,即AC=_________。(2)先画一条射线AP,在射线AP上画AB=a,在AB上画线段AD= b,则线段DB就是线段a与b的 _____,即DB=_________。 【小结】两条线段的和或差就是它们______的和或差。【跟踪练习】要求先独立思考,自主完成,再与对子交流互查,最后通过展示展讲或质疑解决。如图,点A、点B、点C、点D在同一直线上,则AB+BC=___; AD-CD=___; BC= -AB =BD - 。若AB=BC=CD,你能找出哪些等量关系?________________。 ( http: / / www.21cnjy.com )二、知识点2.线段的倍与分1.(尺规作图)已知线段b ( http: / / www.21cnjy.com )。(1)先画射线AP,在射线AP上依次画出线段AB=BC=CD=DE=b。(2)则有AC=( )AB, AD=( )AB, AE=( )AB,AB=1/2( ) , AB= 1 ( http: / / www.21cnjy.com )/3( ) , AB=1/4( ),此时就把点B叫做线段AC的___点;把点B、C叫做线段AD的______点;把点B、C、D叫做线段AE的______点。依次类推。 【小结】1.线段中点定义:线段_____(上或外)一点,如果此点把已知线段分成两条 _____ 的线段,那么就把此点叫做已知线段的中点。线段中点的几何语言(也叫推理形式或解证题的应用格式)如图(1)∵点M是线段AB的中点 (2)∵AM=BM=1/2AB ∴_____=______=1/2_____ ∴点____是线段AB的中点 说明:这是几何中的正、反两种推理形式。∵和∴是两种数学符号, ∵表示“因为“,∴表示“ 所以“,用起来很方便。【跟踪练习】要求先独立思考,自主完成,再与对子交流互查,最后展示解决1.如图,点M是AB的中点,若AM=8cm,则BM=________cm,AB=_____cm。 2.如图,已知点C是线段AB的中点,点D是线段AC的中点,(1)AB= BC (2)BC= AD (3)BD=_____AD 三、自学课本73页的例1、例2,然后回答:1.例1____(是或不是)尺规作图,理由是_________。应注意画图后应写_______。2.通过例2可以感知几何解题说理过程的书写方法为:从______出发,运用所学定义、性质等进行合理推理。【探究案】【学法指导】第一步:独立思考,写出答案 第二步:与对子、小组交流、讨论、互查; 第三步:通过展示展讲,师生点评; 第四步:总结解题思想方法;温馨提示:做题时可以画草图解答,请画在该题附近。点A、B、C都是直线h上的点,且点 ( http: / / www.21cnjy.com )B、C依次在点A的同侧,AB=6 cm,BC=4cm, O是AC的中点,则O、B两点间的距离是______ cm。在直线h上取A、B、C三点,使得AB=6 cm,BC=4 cm。如果O是线段AC的中点,则OB=_____ cm。【小结】第2题运用的数学思想方法是____________。【训练案】题组一1.已知AB=5 cm,延长AB到C,使BC=2.4 cm,在找出AC的中点O,则CO= ____ cm,OB=____ cm。2. 如图,B、C为线段AD上的两点,点C为线段AD的中点AC=5cm,BD=6cm,则线段AB=____ cm。3.在直线h上取M、N、O三点,使得MN=10cm,NO=8cm。如果P是线段MO的中点,则PN=_____ cm。题组二 1.如图AD=7cm,CB=7cm。AC与DB相等吗?请说明理由。 解(1)__________。 ∵AD=7, CB=7 (已知) ∴___=___ (等量代换) ∴AD-___=CB-___ (等式的性质) ∴AC=BD 【总结与反思】【学法指导】可以总结本节课的重点内容,也可以使自己总结的方法、易错点、感受。____________________________________________________________________________________________________【检测案】【学习要求】根据自己的能力选择测试题,1、2、3为必做题,4为选作题。已知如图,点C是线段AB的中点,AB=4cm,BD=1cm,则CD的长度为_____ cm。2. 在一条直线上取D、E、F三点,使DE=5cm,EF=2cm,并且取线段DF的中点O,则线段OE=______ cm。3.如图,已知线段a和 b。(要求:尺规作图) 画线段EF,使EF=a+2b画线段PH,使PH=3b-a 4. 点P是线段MN上一点,点Q是NP的中点,MQ=6,则MP+MN=__布置作业:必做题 1. 课本74页A组第3题。2.如图AC=BD,M是CD的中点,那么M是AB的中点吗?请说明理由。 解:M___AB的中点。 ∵M是CD的中点(已知) ∴___=___ (中点定义)∵AC=BD (已知) ∴AC+CM=BD+DM ( ) ∴___=____ ∴M___AB的中点 (中点定义)选做题 课本74页B组第2题。
A
B
M
A
B
M
B
C
D
A
D
C
B
A
D
C
B
A
C
D
B
A
b
a
M
D
C
B
A
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
