17.1.2 勾股定理的应用同步练习(含答案)
文档属性
| 名称 | 17.1.2 勾股定理的应用同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-09 18:26:11 | ||
图片预览



文档简介
17.1 勾股定理
第2课时 勾股定理的应用
一、选择题
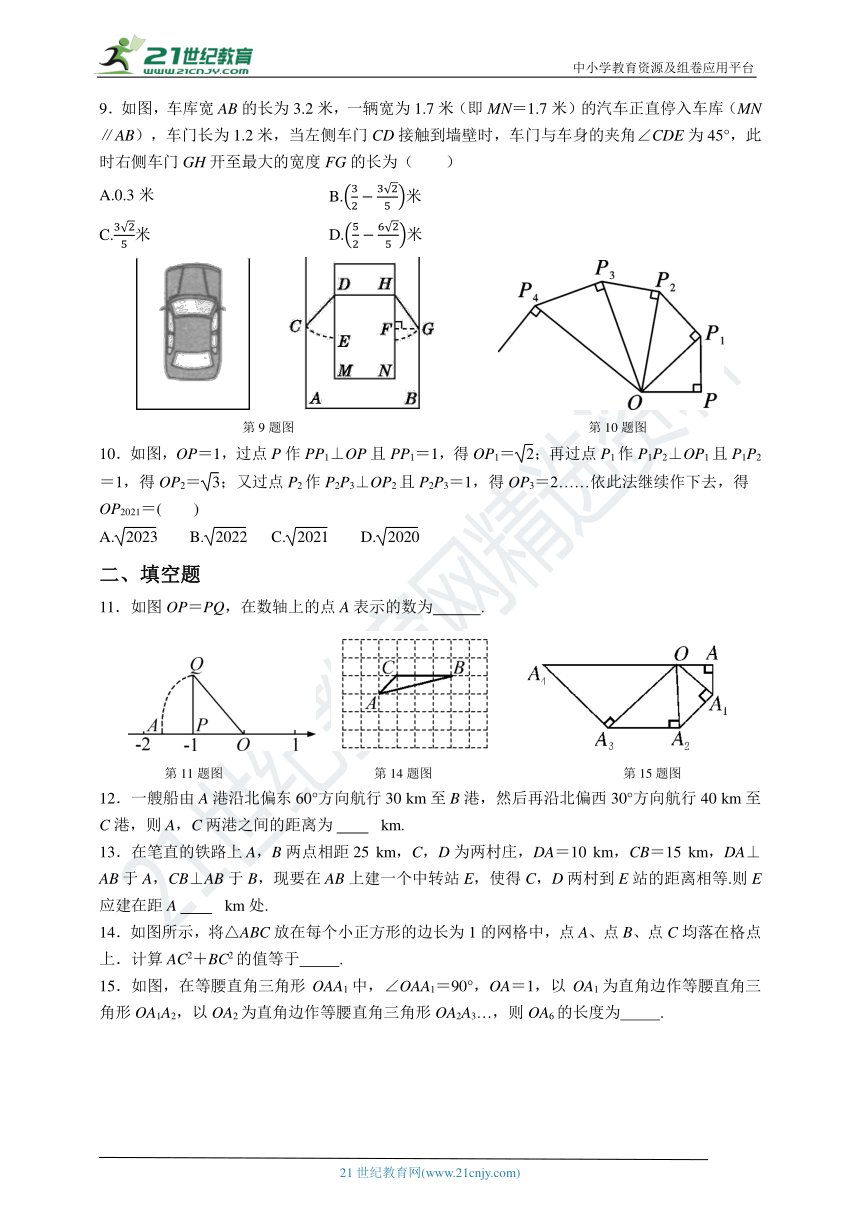
1.一架高2.5m的木梯,斜立在一竖直的墙边,梯脚距墙底0.7m,这时梯子达到的高度是( )
A.2.5m B.2.4m C.2m D.1.8m
2.为准备召开新年晚会,大宏搬来一架高2.5 m的木梯,准备把拉花挂到2.4 m高的墙上,则梯脚与墙角的距离为( )
A.0.7 m B.0.8 m C.0.9 m D.1.0 m
3.如图,一棵树在离地面4.5m处断裂,树的顶部落在离底部6m处.则这棵树折断之前有( )
A.10.5m B.7.5m C.12m D.8m
第3题图 第4题图
4.如图,一圆柱体的底面周长为24cm,高AB为5cm,BC是直径,一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程大约是( )
A.6cm B.12cm C.13cm D.16cm
5.在数轴上作,最简捷的步骤是( )
A.作→→…→ B.作3和2
C.作→→→→,再作→→ D.作4和
6.为迎接新年的到来,同学们做了许多拉花布置教室,准备召开新年晚会,大宏搬来一架高2.5m的木梯,准备把拉花挂到2.4m高的墙上,则梯脚与墙角距离为( )
A.0.7m B.0.8m C.0.9m D.1.0m
7.如图,在一个高为5 m,长为13 m的楼梯表面铺地毯,则地毯长度至少应是( )
A.13 m B.17 m C.18 m D.25 m
第7题图 第8题图
8.如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )
A.12≤a≤13 B.12≤a≤15 C.5≤a≤12 D.5≤a≤13
9.如图,车库宽AB的长为3.2米,一辆宽为1.7米(即MN=1.7米)的汽车正直停入车库(MN∥AB),车门长为1.2米,当左侧车门CD接触到墙壁时,车门与车身的夹角∠CDE为45°,此时右侧车门GH开至最大的宽度FG的长为( )
A.0.3米 B.米
C.米 D.米
第9题图 第10题图
10.如图,OP=1,过点P作PP1⊥OP且PP1=1,得OP1=;再过点P1作P1P2⊥OP1且P1P2=1,得OP2=;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2……依此法继续作下去,得OP2021=( )
A. B. C. D.
二、填空题
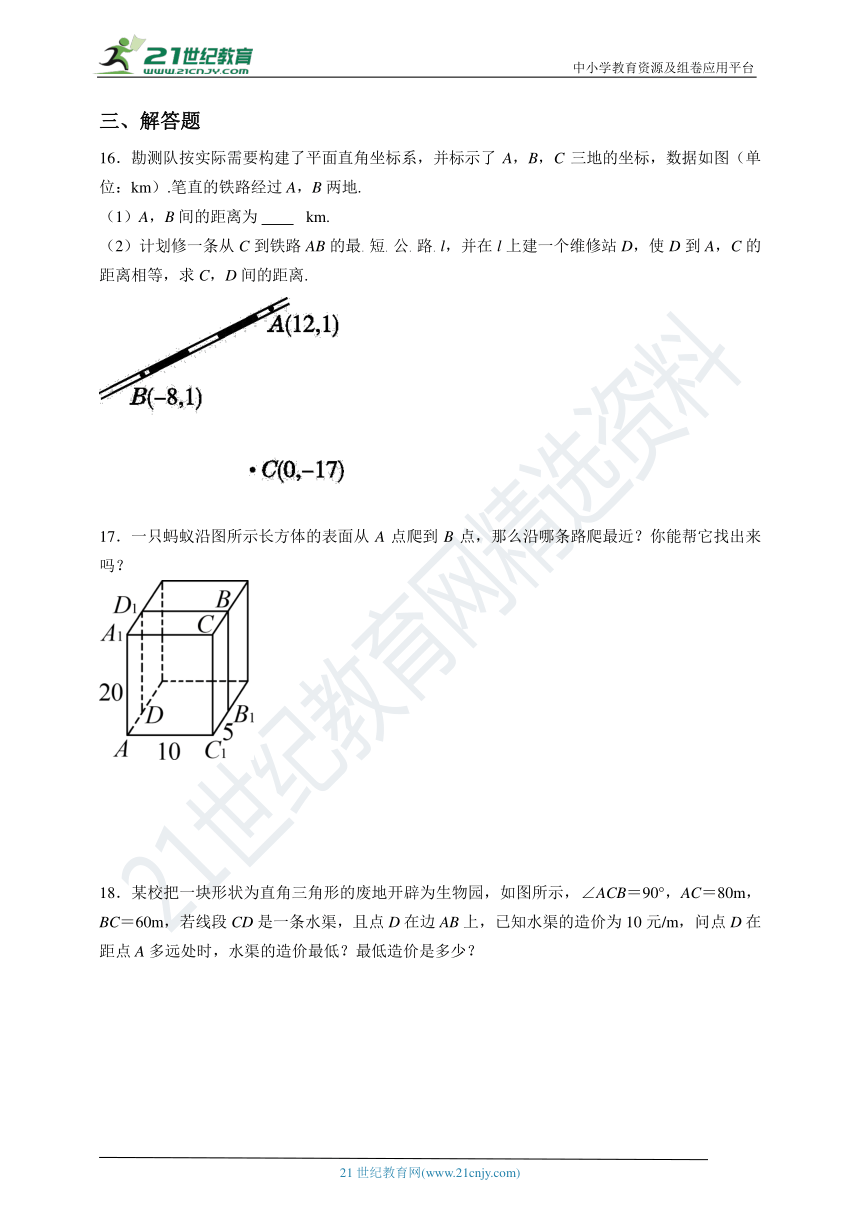
11.如图OP=PQ,在数轴上的点A表示的数为 .
第11题图 第14题图 第15题图
12.一艘船由A港沿北偏东60°方向航行30 km至B港,然后再沿北偏西30°方向航行40 km至C港,则A,C两港之间的距离为 km.
13.在笔直的铁路上A,B两点相距25 km,C,D为两村庄,DA=10 km,CB=15 km,DA⊥AB于A,CB⊥AB于B,现要在AB上建一个中转站E,使得C,D两村到E站的距离相等.则E应建在距A km处.
14.如图所示,将△ABC放在每个小正方形的边长为1的网格中,点A、点B、点C均落在格点上.计算AC2+BC2的值等于 .
15.如图,在等腰直角三角形OAA1中,∠OAA1=90°,OA=1,以OA1为直角边作等腰直角三角形OA1A2,以OA2为直角边作等腰直角三角形OA2A3…,则OA6的长度为 .
三、解答题
16.勘测队按实际需要构建了平面直角坐标系,并标示了A,B,C三地的坐标,数据如图(单位:km).笔直的铁路经过A,B两地.
(1)A,B间的距离为 km.
(2)计划修一条从C到铁路AB的最.短.公.路.l,并在l上建一个维修站D,使D到A,C的距离相等,求C,D间的距离.
17.一只蚂蚁沿图所示长方体的表面从A点爬到B点,那么沿哪条路爬最近?你能帮它找出来吗?
18.某校把一块形状为直角三角形的废地开辟为生物园,如图所示,∠ACB=90°,AC=80m,BC=60m,若线段CD是一条水渠,且点D在边AB上,已知水渠的造价为10元/m,问点D在距点A多远处时,水渠的造价最低?最低造价是多少?
19.台风是一种自然灾害,它以台风中心为圆心在周围数十千米范围内形成气旋风暴,有极强的破坏力.如图所示,据气象观测,在沿海某城市A的正南方向220千米的B处有一台风中心,其中心最大风力为12级,每远离台风中心20千米,风力就会减弱一级.该台风中心现正以15千米/时的速度沿北偏东30°方向往C移动,且台风中心风力不变(若城市所受风力达到或超过4级,则称为受台风影响).
(1)该城市是否受到这次台风的影响?请说明理由;
(2)若会受到台风影响,那么台风影响该城市的持
续时间有多长?
(3)该城市受到台风影响的最大风力为几级?
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.一架高2.5m的木梯,斜立在一竖直的墙边,梯脚距墙底0.7m,这时梯子达到的高度是( B )
A.2.5m B.2.4m C.2m D.1.8m
2.为准备召开新年晚会,大宏搬来一架高2.5 m的木梯,准备把拉花挂到2.4 m高的墙上,则梯脚与墙角的距离为( A )
A.0.7 m B.0.8 m C.0.9 m D.1.0 m
3.如图,一棵树在离地面4.5m处断裂,树的顶部落在离底部6m处.则这棵树折断之前有( C )
A.10.5m B.7.5m C.12m D.8m
第3题图 第4题图
4.如图,一圆柱体的底面周长为24cm,高AB为5cm,BC是直径,一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程大约是( C )
A.6cm B.12cm C.13cm D.16cm
5.在数轴上作,最简捷的步骤是( B )
A.作→→…→ B.作3和2
C.作→→→→,再作→→ D.作4和
6.为迎接新年的到来,同学们做了许多拉花布置教室,准备召开新年晚会,大宏搬来一架高2.5m的木梯,准备把拉花挂到2.4m高的墙上,则梯脚与墙角距离为( A )
A.0.7m B.0.8m C.0.9m D.1.0m
7.如图,在一个高为5 m,长为13 m的楼梯表面铺地毯,则地毯长度至少应是( B )
A.13 m B.17 m C.18 m D.25 m
第7题图 第8题图
8.如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( A )
A.12≤a≤13 B.12≤a≤15 C.5≤a≤12 D.5≤a≤13
9.如图,车库宽AB的长为3.2米,一辆宽为1.7米(即MN=1.7米)的汽车正直停入车库(MN∥AB),车门长为1.2米,当左侧车门CD接触到墙壁时,车门与车身的夹角∠CDE为45°,此时右侧车门GH开至最大的宽度FG的长为( B )
A.0.3米 B.米
C.米 D.米
【解析】过点C作CO⊥DM于O,∴∠COD=90°,∴CO2+DO2=CD2.∵∠CDE=45°,∴∠DCO=45°=∠CDE,
∴CO=DO.∴2CO2=CD2=1.22,∴CO=(米).
易知AB=MN+CO+FG,
∴FG=3.2-1.7-=(米),故选B.
第9题图 第10题图
10.如图,OP=1,过点P作PP1⊥OP且PP1=1,得OP1=;再过点P1作P1P2⊥OP1且P1P2=1,得OP2=;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2……依此法继续作下去,得OP2021=( B )
A. B. C. D.
二、填空题
11.如图OP=PQ,在数轴上的点A表示的数为 .
【答案】-
第11题图 第14题图 第15题图
12.一艘船由A港沿北偏东60°方向航行30 km至B港,然后再沿北偏西30°方向航行40 km至C港,则A,C两港之间的距离为 km.
【答案】50
13.在笔直的铁路上A,B两点相距25 km,C,D为两村庄,DA=10 km,CB=15 km,DA⊥AB于A,CB⊥AB于B,现要在AB上建一个中转站E,使得C,D两村到E站的距离相等.则E应建在距A km处.
【答案】15
14.如图所示,将△ABC放在每个小正方形的边长为1的网格中,点A、点B、点C均落在格点上.计算AC2+BC2的值等于 .
【答案】11
15.如图,在等腰直角三角形OAA1中,∠OAA1=90°,OA=1,以OA1为直角边作等腰直角三角形OA1A2,以OA2为直角边作等腰直角三角形OA2A3…,则OA6的长度为 .
【答案】8
三、解答题
16.勘测队按实际需要构建了平面直角坐标系,并标示了A,B,C三地的坐标,数据如图(单位:km).笔直的铁路经过A,B两地.
(1)A,B间的距离为 km.
(2)计划修一条从C到铁路AB的最.短.公.路.l,并在l上建一个维修站D,使D到A,C的距离相等,求C,D间的距离.
解:(1)20
(2)如图,过点C作l⊥AB于点E,连接AC,作AC的垂直平分线交l于点D,连接AD.
易知CE=1-(-17)=18 (km),AE=12 km.
设CD=x km,则AD=CD=x km.
由勾股定理得x2=(18-x)2+122,解得x=13.
故CD=13 km.
17.一只蚂蚁沿图所示长方体的表面从A点爬到B点,那么沿哪条路爬最近?你能帮它找出来吗?
解:将空间图形转化为平面图形,把A和B所在的相邻的两个面展开,用两点间线段最短,求得最短路径有以下三种情况,如图所示:
图(1)中,AB2=AB+BB=152+202=625;图(2)中,AB2=252+102=725;图(3)中,AB2=302+52=925.比较以上结果,最短路程为25cm.
18.某校把一块形状为直角三角形的废地开辟为生物园,如图所示,∠ACB=90°,AC=80m,BC=60m,若线段CD是一条水渠,且点D在边AB上,已知水渠的造价为10元/m,问点D在距点A多远处时,水渠的造价最低?最低造价是多少?
解:当CD为斜边上的高时,CD最短,从而水渠造价最低.∵∠ACB=90°,AC=80m,BC=60m,∴AB===100(m).∵CD·AB=AC·BC,即CD·100=80×60,∴CD=48m,48×10=480(元).在Rt△ACD中,AC=80m,CD=48m,∴AD===64(m),∴点D在距点A 64m的地方时,水渠的造价最低,最低造价为480元.
19.台风是一种自然灾害,它以台风中心为圆心在周围数十千米范围内形成气旋风暴,有极强的破坏力.如图所示,据气象观测,在沿海某城市A的正南方向220千米的B处有一台风中心,其中心最大风力为12级,每远离台风中心20千米,风力就会减弱一级.该台风中心现正以15千米/时的速度沿北偏东30°方向往C移动,且台风中心风力不变(若城市所受风力达到或超过4级,则称为受台风影响).
(1)该城市是否受到这次台风的影响?请说明理由;
(2)若会受到台风影响,那么台风影响该城市的持
续时间有多长?
(3)该城市受到台风影响的最大风力为几级?
解:(1)该城市会受到这次台风的影响,理由:过点A作AD⊥BC,垂足为D.因为AB=220千米,∠B=30°,所以AD=110千米.
根据题意,当点A距台风中心不超过20×(12-4)=160(千米)时,将会受到台风的影响,故该城市会受到这次台风的影响;
(2)设该城市开始受影响点为E,最后受影响点为F.在Rt△ADE中,DE====30(千米),所以EF=2DE=60(千米).因为该台风中心以15千米/时的速度移动,所以台风影响该城市的持续时间为=4(小时);
(3)当台风中心位于D处时,A城市所受这次台风的影响最大,其最大风力为12-=6.5(级).
答:(1)该城市会受到这次台风的影响;(2)台风影响该城市的持续时间为4小时;(3)该城市受到台风影响的最大风力为6.5级.
第2课时 勾股定理的应用
一、选择题
1.一架高2.5m的木梯,斜立在一竖直的墙边,梯脚距墙底0.7m,这时梯子达到的高度是( )
A.2.5m B.2.4m C.2m D.1.8m
2.为准备召开新年晚会,大宏搬来一架高2.5 m的木梯,准备把拉花挂到2.4 m高的墙上,则梯脚与墙角的距离为( )
A.0.7 m B.0.8 m C.0.9 m D.1.0 m
3.如图,一棵树在离地面4.5m处断裂,树的顶部落在离底部6m处.则这棵树折断之前有( )
A.10.5m B.7.5m C.12m D.8m
第3题图 第4题图
4.如图,一圆柱体的底面周长为24cm,高AB为5cm,BC是直径,一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程大约是( )
A.6cm B.12cm C.13cm D.16cm
5.在数轴上作,最简捷的步骤是( )
A.作→→…→ B.作3和2
C.作→→→→,再作→→ D.作4和
6.为迎接新年的到来,同学们做了许多拉花布置教室,准备召开新年晚会,大宏搬来一架高2.5m的木梯,准备把拉花挂到2.4m高的墙上,则梯脚与墙角距离为( )
A.0.7m B.0.8m C.0.9m D.1.0m
7.如图,在一个高为5 m,长为13 m的楼梯表面铺地毯,则地毯长度至少应是( )
A.13 m B.17 m C.18 m D.25 m
第7题图 第8题图
8.如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )
A.12≤a≤13 B.12≤a≤15 C.5≤a≤12 D.5≤a≤13
9.如图,车库宽AB的长为3.2米,一辆宽为1.7米(即MN=1.7米)的汽车正直停入车库(MN∥AB),车门长为1.2米,当左侧车门CD接触到墙壁时,车门与车身的夹角∠CDE为45°,此时右侧车门GH开至最大的宽度FG的长为( )
A.0.3米 B.米
C.米 D.米
第9题图 第10题图
10.如图,OP=1,过点P作PP1⊥OP且PP1=1,得OP1=;再过点P1作P1P2⊥OP1且P1P2=1,得OP2=;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2……依此法继续作下去,得OP2021=( )
A. B. C. D.
二、填空题
11.如图OP=PQ,在数轴上的点A表示的数为 .
第11题图 第14题图 第15题图
12.一艘船由A港沿北偏东60°方向航行30 km至B港,然后再沿北偏西30°方向航行40 km至C港,则A,C两港之间的距离为 km.
13.在笔直的铁路上A,B两点相距25 km,C,D为两村庄,DA=10 km,CB=15 km,DA⊥AB于A,CB⊥AB于B,现要在AB上建一个中转站E,使得C,D两村到E站的距离相等.则E应建在距A km处.
14.如图所示,将△ABC放在每个小正方形的边长为1的网格中,点A、点B、点C均落在格点上.计算AC2+BC2的值等于 .
15.如图,在等腰直角三角形OAA1中,∠OAA1=90°,OA=1,以OA1为直角边作等腰直角三角形OA1A2,以OA2为直角边作等腰直角三角形OA2A3…,则OA6的长度为 .
三、解答题
16.勘测队按实际需要构建了平面直角坐标系,并标示了A,B,C三地的坐标,数据如图(单位:km).笔直的铁路经过A,B两地.
(1)A,B间的距离为 km.
(2)计划修一条从C到铁路AB的最.短.公.路.l,并在l上建一个维修站D,使D到A,C的距离相等,求C,D间的距离.
17.一只蚂蚁沿图所示长方体的表面从A点爬到B点,那么沿哪条路爬最近?你能帮它找出来吗?
18.某校把一块形状为直角三角形的废地开辟为生物园,如图所示,∠ACB=90°,AC=80m,BC=60m,若线段CD是一条水渠,且点D在边AB上,已知水渠的造价为10元/m,问点D在距点A多远处时,水渠的造价最低?最低造价是多少?
19.台风是一种自然灾害,它以台风中心为圆心在周围数十千米范围内形成气旋风暴,有极强的破坏力.如图所示,据气象观测,在沿海某城市A的正南方向220千米的B处有一台风中心,其中心最大风力为12级,每远离台风中心20千米,风力就会减弱一级.该台风中心现正以15千米/时的速度沿北偏东30°方向往C移动,且台风中心风力不变(若城市所受风力达到或超过4级,则称为受台风影响).
(1)该城市是否受到这次台风的影响?请说明理由;
(2)若会受到台风影响,那么台风影响该城市的持
续时间有多长?
(3)该城市受到台风影响的最大风力为几级?
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.一架高2.5m的木梯,斜立在一竖直的墙边,梯脚距墙底0.7m,这时梯子达到的高度是( B )
A.2.5m B.2.4m C.2m D.1.8m
2.为准备召开新年晚会,大宏搬来一架高2.5 m的木梯,准备把拉花挂到2.4 m高的墙上,则梯脚与墙角的距离为( A )
A.0.7 m B.0.8 m C.0.9 m D.1.0 m
3.如图,一棵树在离地面4.5m处断裂,树的顶部落在离底部6m处.则这棵树折断之前有( C )
A.10.5m B.7.5m C.12m D.8m
第3题图 第4题图
4.如图,一圆柱体的底面周长为24cm,高AB为5cm,BC是直径,一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程大约是( C )
A.6cm B.12cm C.13cm D.16cm
5.在数轴上作,最简捷的步骤是( B )
A.作→→…→ B.作3和2
C.作→→→→,再作→→ D.作4和
6.为迎接新年的到来,同学们做了许多拉花布置教室,准备召开新年晚会,大宏搬来一架高2.5m的木梯,准备把拉花挂到2.4m高的墙上,则梯脚与墙角距离为( A )
A.0.7m B.0.8m C.0.9m D.1.0m
7.如图,在一个高为5 m,长为13 m的楼梯表面铺地毯,则地毯长度至少应是( B )
A.13 m B.17 m C.18 m D.25 m
第7题图 第8题图
8.如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( A )
A.12≤a≤13 B.12≤a≤15 C.5≤a≤12 D.5≤a≤13
9.如图,车库宽AB的长为3.2米,一辆宽为1.7米(即MN=1.7米)的汽车正直停入车库(MN∥AB),车门长为1.2米,当左侧车门CD接触到墙壁时,车门与车身的夹角∠CDE为45°,此时右侧车门GH开至最大的宽度FG的长为( B )
A.0.3米 B.米
C.米 D.米
【解析】过点C作CO⊥DM于O,∴∠COD=90°,∴CO2+DO2=CD2.∵∠CDE=45°,∴∠DCO=45°=∠CDE,
∴CO=DO.∴2CO2=CD2=1.22,∴CO=(米).
易知AB=MN+CO+FG,
∴FG=3.2-1.7-=(米),故选B.
第9题图 第10题图
10.如图,OP=1,过点P作PP1⊥OP且PP1=1,得OP1=;再过点P1作P1P2⊥OP1且P1P2=1,得OP2=;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2……依此法继续作下去,得OP2021=( B )
A. B. C. D.
二、填空题
11.如图OP=PQ,在数轴上的点A表示的数为 .
【答案】-
第11题图 第14题图 第15题图
12.一艘船由A港沿北偏东60°方向航行30 km至B港,然后再沿北偏西30°方向航行40 km至C港,则A,C两港之间的距离为 km.
【答案】50
13.在笔直的铁路上A,B两点相距25 km,C,D为两村庄,DA=10 km,CB=15 km,DA⊥AB于A,CB⊥AB于B,现要在AB上建一个中转站E,使得C,D两村到E站的距离相等.则E应建在距A km处.
【答案】15
14.如图所示,将△ABC放在每个小正方形的边长为1的网格中,点A、点B、点C均落在格点上.计算AC2+BC2的值等于 .
【答案】11
15.如图,在等腰直角三角形OAA1中,∠OAA1=90°,OA=1,以OA1为直角边作等腰直角三角形OA1A2,以OA2为直角边作等腰直角三角形OA2A3…,则OA6的长度为 .
【答案】8
三、解答题
16.勘测队按实际需要构建了平面直角坐标系,并标示了A,B,C三地的坐标,数据如图(单位:km).笔直的铁路经过A,B两地.
(1)A,B间的距离为 km.
(2)计划修一条从C到铁路AB的最.短.公.路.l,并在l上建一个维修站D,使D到A,C的距离相等,求C,D间的距离.
解:(1)20
(2)如图,过点C作l⊥AB于点E,连接AC,作AC的垂直平分线交l于点D,连接AD.
易知CE=1-(-17)=18 (km),AE=12 km.
设CD=x km,则AD=CD=x km.
由勾股定理得x2=(18-x)2+122,解得x=13.
故CD=13 km.
17.一只蚂蚁沿图所示长方体的表面从A点爬到B点,那么沿哪条路爬最近?你能帮它找出来吗?
解:将空间图形转化为平面图形,把A和B所在的相邻的两个面展开,用两点间线段最短,求得最短路径有以下三种情况,如图所示:
图(1)中,AB2=AB+BB=152+202=625;图(2)中,AB2=252+102=725;图(3)中,AB2=302+52=925.比较以上结果,最短路程为25cm.
18.某校把一块形状为直角三角形的废地开辟为生物园,如图所示,∠ACB=90°,AC=80m,BC=60m,若线段CD是一条水渠,且点D在边AB上,已知水渠的造价为10元/m,问点D在距点A多远处时,水渠的造价最低?最低造价是多少?
解:当CD为斜边上的高时,CD最短,从而水渠造价最低.∵∠ACB=90°,AC=80m,BC=60m,∴AB===100(m).∵CD·AB=AC·BC,即CD·100=80×60,∴CD=48m,48×10=480(元).在Rt△ACD中,AC=80m,CD=48m,∴AD===64(m),∴点D在距点A 64m的地方时,水渠的造价最低,最低造价为480元.
19.台风是一种自然灾害,它以台风中心为圆心在周围数十千米范围内形成气旋风暴,有极强的破坏力.如图所示,据气象观测,在沿海某城市A的正南方向220千米的B处有一台风中心,其中心最大风力为12级,每远离台风中心20千米,风力就会减弱一级.该台风中心现正以15千米/时的速度沿北偏东30°方向往C移动,且台风中心风力不变(若城市所受风力达到或超过4级,则称为受台风影响).
(1)该城市是否受到这次台风的影响?请说明理由;
(2)若会受到台风影响,那么台风影响该城市的持
续时间有多长?
(3)该城市受到台风影响的最大风力为几级?
解:(1)该城市会受到这次台风的影响,理由:过点A作AD⊥BC,垂足为D.因为AB=220千米,∠B=30°,所以AD=110千米.
根据题意,当点A距台风中心不超过20×(12-4)=160(千米)时,将会受到台风的影响,故该城市会受到这次台风的影响;
(2)设该城市开始受影响点为E,最后受影响点为F.在Rt△ADE中,DE====30(千米),所以EF=2DE=60(千米).因为该台风中心以15千米/时的速度移动,所以台风影响该城市的持续时间为=4(小时);
(3)当台风中心位于D处时,A城市所受这次台风的影响最大,其最大风力为12-=6.5(级).
答:(1)该城市会受到这次台风的影响;(2)台风影响该城市的持续时间为4小时;(3)该城市受到台风影响的最大风力为6.5级.
