8.4.1 平面的基本性质 课件(共22张PPT)
文档属性
| 名称 | 8.4.1 平面的基本性质 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-09 20:47:24 | ||
图片预览


文档简介
(共22张PPT)
空间点、直线、平面之间的位置关系
8.4.1 平面的基本性质
情境引入
几何里所说的“平面”就是从这样的一些物体中抽象出来的.
在初中,我们已经对点和直线有了一定的认识,知道它们都是由现实事物抽象得到的,平面是构成我们生活的空间的基本元素之一,增加了对平面的研究,几何的学习就由二维到三维.你能举例说明,生活中哪些物体给我们平面的感觉呢?
新知探究
和点、直线一样,平面也是从现实世界中抽象出来的不加定义的最基本的几何概念.那么,类比直线的“直”和向两端“无限延伸”的特征,平面有哪些特征呢?
平面是“平”的;
平面可以向四周“无限延伸”.
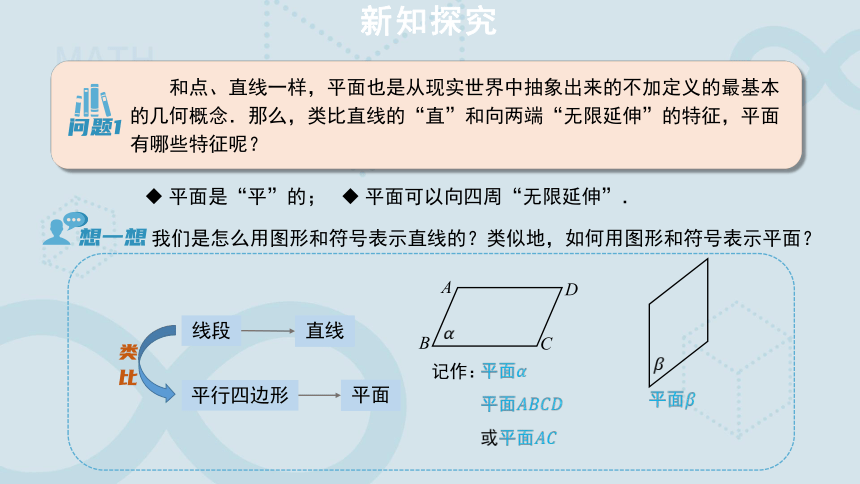
我们是怎么用图形和符号表示直线的?类似地,如何用图形和符号表示平面?
平面
平面
平面
记作:
A
B
C
D
线段
直线
平行四边形
平面
新知探究
和点、直线一样,平面也是从现实世界中抽象出来的不加定义的最基本的几何概念.那么,类比直线的“直”和向两端“无限延伸”的特征,平面有哪些特征呢?
平面是“平”的;
平面可以向四周“无限延伸”.
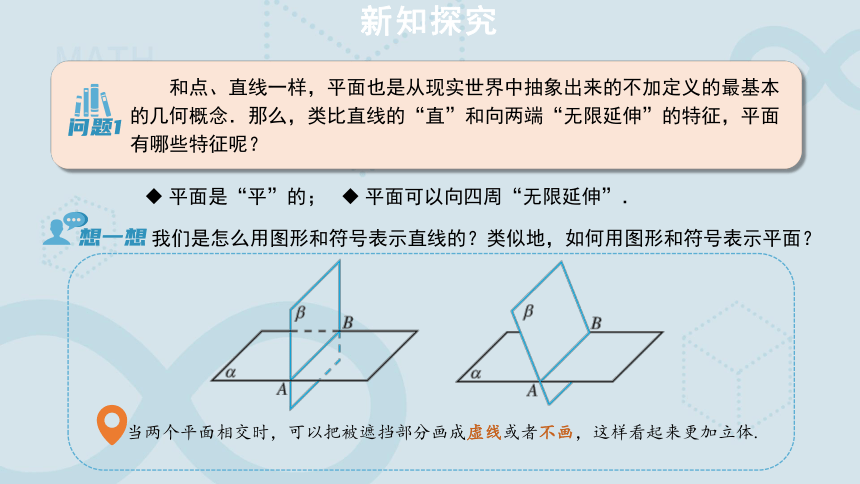
我们是怎么用图形和符号表示直线的?类似地,如何用图形和符号表示平面?
当两个平面相交时,可以把被遮挡部分画成虚线或者不画,这样看起来更加立体.
新知探究
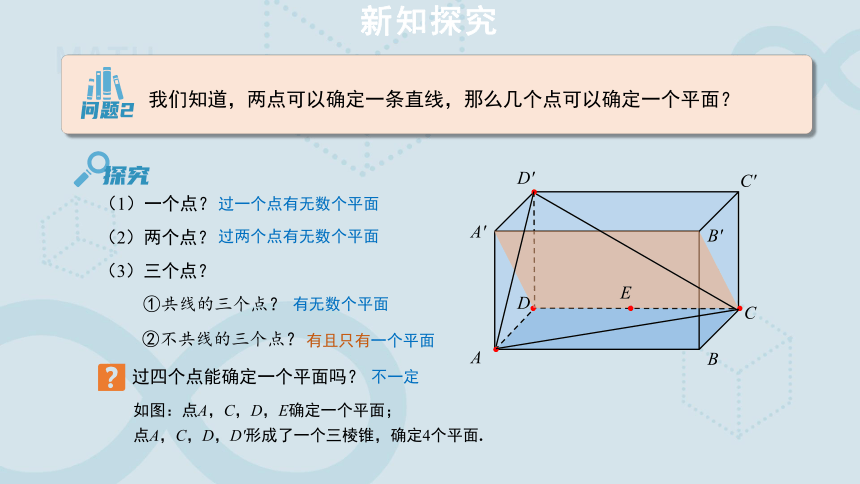
(1)一个点?
过一个点有无数个平面
A′
D′
B′
C′
A
B
C
D
(2)两个点?
过两个点有无数个平面
(3)三个点?
①共线的三个点?
E
有无数个平面
②不共线的三个点?
有且只有一个平面
过四个点能确定一个平面吗?
如图:点A,C,D,E确定一个平面;
点A,C,D,D'形成了一个三棱锥,确定4个平面.
不一定
我们知道,两点可以确定一条直线,那么几个点可以确定一个平面?
新知探究
存在性
唯一性
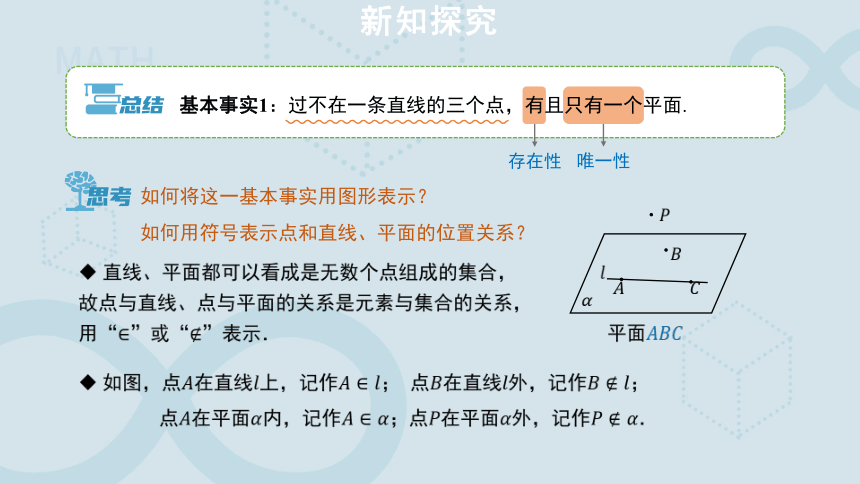
如何将这一基本事实用图形表示?
平面
如何用符号表示点和直线、平面的位置关系?
直线、平面都可以看成是无数个点组成的集合,
故点与直线、点与平面的关系是元素与集合的关系,
用“”或“”表示.
如图,点在直线上,记作; 点在直线外,记作;
点在平面内,记作;点在平面外,记作.
基本事实1:过不在一条直线的三个点,有且只有一个平面.
新知探究
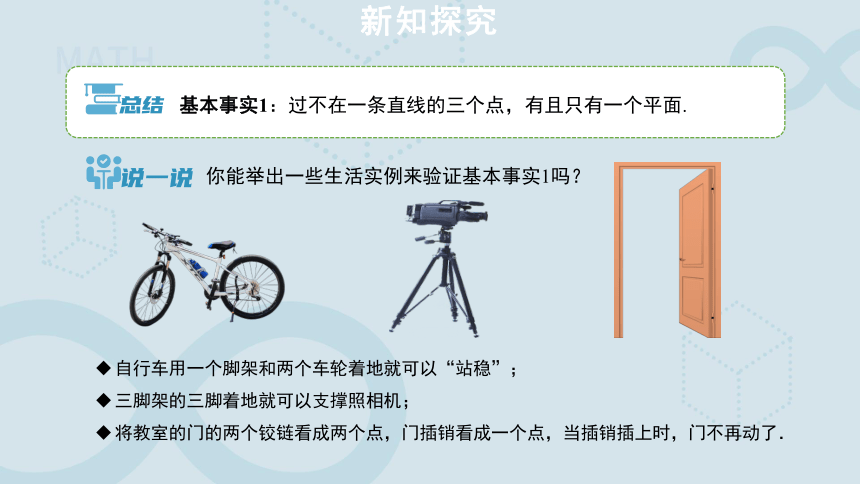
你能举出一些生活实例来验证基本事实1吗?
基本事实1:过不在一条直线的三个点,有且只有一个平面.
自行车用一个脚架和两个车轮着地就可以“站稳”;
三脚架的三脚着地就可以支撑照相机;
将教室的门的两个铰链看成两个点,门插销看成一个点,当插销插上时,门不再动了.
新知探究
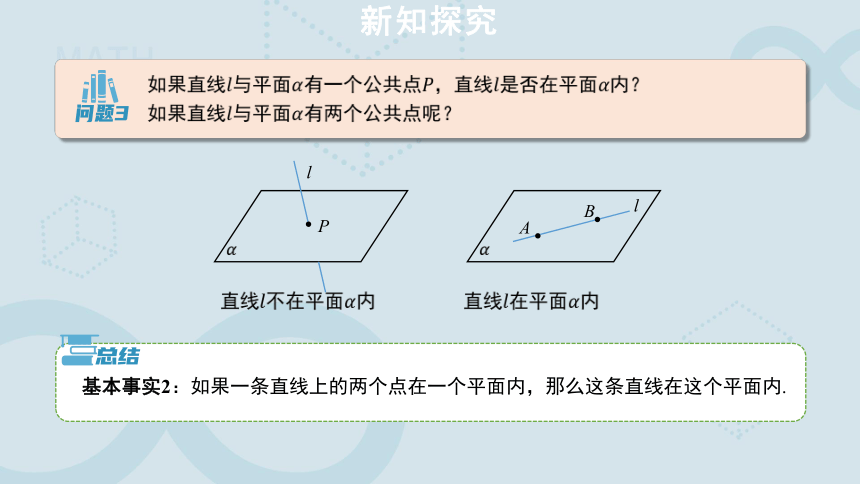
如果直线与平面有一个公共点,直线是否在平面内?
如果直线与平面有两个公共点呢?
P
l
A
B
l
直线不在平面内
直线在平面内
基本事实2:如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内.
新知探究
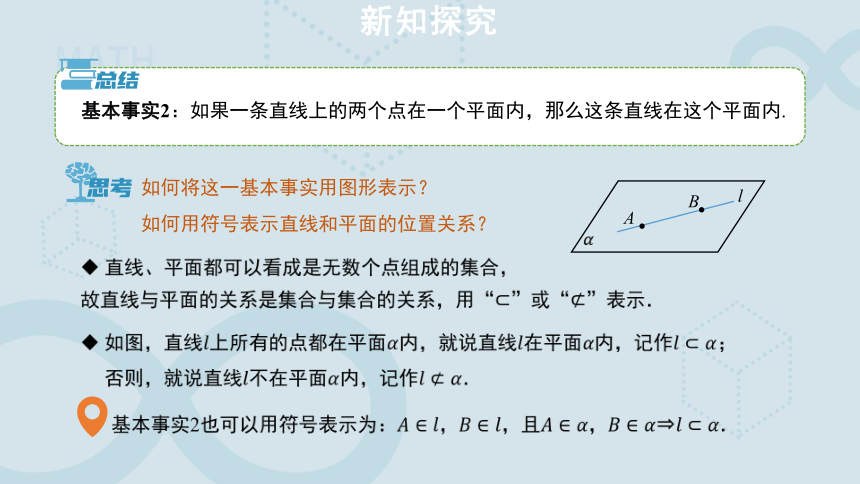
基本事实2:如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内.
如何将这一基本事实用图形表示?
如何用符号表示直线和平面的位置关系?
A
B
l
直线、平面都可以看成是无数个点组成的集合,
故直线与平面的关系是集合与集合的关系,用“”或“”表示.
如图,直线上所有的点都在平面内,就说直线在平面内,记作;
否则,就说直线不在平面内,记作.
基本事实2也可以用符号表示为:,,且, .
给定不共线三点,,确定一个平面;
由基本事实2,直线,,都在平面内,
进而连接这三条直线上任意两点所得直线也都在平面内,
所有这些直线可以编织成一个“直线网”,这个“直线网”可以铺满平面.
组成这个“直线网”的直线的“直”和向各个方向无限延伸,说明了平面的“平”和“无限延展”.
新知探究
我们知道,平面具有“平”和“无限延展”的特征,而基本事实2反映了直线与平面的位置关系,我们能不能利用这种位置关系,用直线的“直”和“无限延伸”刻画平面的“平”和“无限延展”?
把三角尺的一个角立在课桌面上,三角尺所在平面与课桌面所在平面是否只相交于一点?为什么?
新知探究
平面是无限延展的,适当补出三角尺所在平面
两平面交于一条直线
不止一个公共点,这些公共点是共线的
你还能举出生活中其它平面与平面相交的例子吗?
教室相邻的两个墙面在地面的墙角处有一个公共点,这两个墙面相交于过这个点的一条直线等.
新知探究
基本事实3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
P
l
P,P
符号语言:
结合基本事实3,你能进一步说明平面的“平”和“无限延展”的特征吗?
基本事实3说明:如果两个平面有一个公共点,那么这两个平面一定相交于过这个公共点的一条直线.两个平面相交成一条直线的事实,可以让我们进一步认识了平面的“平”和“无限延展”.
基本事实1给出了确定一个平面的一种方法.利用基本事实1和基本事实2,再结合“两点确定一条直线”,你还可以得到一些确定一个平面的方法吗?
新知探究
(1)
A
B
C
a
b
a
(2)
P
(3)
b
a
A
B
C
如图(1),设点是直线外一点,在直线上任取两点和,
则由基本事实1,经过,,三点确定一个平面,
再由基本事实2,直线也在平面内,
因此平面经过直线和点,即一条直线和这条直线外一点确定一个平面.
A
B
C
新知探究
推论1:一条直线和该直线外一点确定一个平面;
推论2:两条相交直线确定一个平面;
推论3:两条平行直线确定一个平面确定一个平面;
基本事实1:过不在一条直线的三个点,有且只有一个平面.
确定平面的依据!
应用举例
用符号表示下列语句,并画出图形:
(1)点在平面内但在平面外,平面相交于直线;
(2)直线经过平面内一点,外一点;
(3)直线在平面内,也在平面内.
文字语言
符号语言
图形语言
转 化
转 化
解:(1),. (如图①)
(2),,,,.(如图②)
(3).(如图③)
A
l
①
A
B
a
②
③
应用举例
已知:,,,.
求证:直线,,共面.
A
l
B
C
D
因为直线与点可以确定平面,
所以只需证明,,都在平面内.
证明:因为,所以与可以确定平面(推论1).
因为,所以.
又,所以(基本事实2).
同理,,所以,,在同一平面内,即它们共面.
应用举例
如图,在长方体中,为棱的中点,画出由,,三点所确定的平面与长方体表面的交线.
因为点既在平面内又在平面内,
所以点在平面与平面的交线上.
同理,点在平面与平面的交线上.
因此,就是平面与平面的交线.
作法:连接,,,它们就是平面与长方体表面的交线.
A
B
C
D
A1
B1
C1
D1
P
课堂练习
判断正误,并说明理由:
(1)平面与平面相交,它们只有有限个公共点.
(2)一个点和一条直线确定一个平面.
(3)两两相交的三条直线确定一个平面.
(4)如果两个平面有三个不共线的公共点,那么这两个平面重合.
根据基本事实3,两平面交于一条直线,有无限个公共点.
根据推论1,只有当点在线外,才能确定一个平面,若点在线上,则确定无数个平面.
若交点不重合,则能确定一个平面,若交点重合,则可能确定三个平面.
若两平面平行,无公共点;若两平面相交,则交点共线.
课堂练习
下列推理错误的是( )
A.
B.,
C.
D.
根据点、线、面的位置关系确定即可
A选项,,可能,所以A选项推理错误.
B选项,根据基本事实2可知,B选项正确.
C选项,因为,所以所以,C选项正确.
D选项,显然正确.
A
课堂练习
如图,正四棱柱ABCD-A′B′C′D′中,过对角线AC′的截面为菱形AEC′F,试着画出截面AEC′F与底面ABCD的交线.
C
B
A
D
E
C′
D′
B′
A′
F
M
N
延长CB、C′E交于点M,
延长CD、C′F交于点N,
连接MN,
则平面C′MN即截面AEC′F,
故MN即所需画的交线.
课堂练习
若直线l与平面相交于点O,,且AC∥BD,则三点的位置关系是 .
共线
D
O
C
B
A
l
如图,∵AC∥BD
∴AC,BD确定一个平面,设为平面
则C,D,l均在平面内
∵点O在直线l上
∴点O在平面内
又点O,C,D在平面内
∴平面,相交于O,C,D所在直线(基本事实3)
故O,C,D三点共线
归纳总结
回顾本节课的探究过程,你学到了什么?
基本事实
基本事实1:过不在一条直线的三个点,有且只有一个平面.
基本事实2:如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内.
基本事实3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
推论1:一条直线和该直线外一点确定一个平面.
推论2:两条相交直线确定一个平面.
推论3:两条平行直线确定一个平面.
空间点、直线、平面之间的位置关系
8.4.1 平面的基本性质
情境引入
几何里所说的“平面”就是从这样的一些物体中抽象出来的.
在初中,我们已经对点和直线有了一定的认识,知道它们都是由现实事物抽象得到的,平面是构成我们生活的空间的基本元素之一,增加了对平面的研究,几何的学习就由二维到三维.你能举例说明,生活中哪些物体给我们平面的感觉呢?
新知探究
和点、直线一样,平面也是从现实世界中抽象出来的不加定义的最基本的几何概念.那么,类比直线的“直”和向两端“无限延伸”的特征,平面有哪些特征呢?
平面是“平”的;
平面可以向四周“无限延伸”.
我们是怎么用图形和符号表示直线的?类似地,如何用图形和符号表示平面?
平面
平面
平面
记作:
A
B
C
D
线段
直线
平行四边形
平面
新知探究
和点、直线一样,平面也是从现实世界中抽象出来的不加定义的最基本的几何概念.那么,类比直线的“直”和向两端“无限延伸”的特征,平面有哪些特征呢?
平面是“平”的;
平面可以向四周“无限延伸”.
我们是怎么用图形和符号表示直线的?类似地,如何用图形和符号表示平面?
当两个平面相交时,可以把被遮挡部分画成虚线或者不画,这样看起来更加立体.
新知探究
(1)一个点?
过一个点有无数个平面
A′
D′
B′
C′
A
B
C
D
(2)两个点?
过两个点有无数个平面
(3)三个点?
①共线的三个点?
E
有无数个平面
②不共线的三个点?
有且只有一个平面
过四个点能确定一个平面吗?
如图:点A,C,D,E确定一个平面;
点A,C,D,D'形成了一个三棱锥,确定4个平面.
不一定
我们知道,两点可以确定一条直线,那么几个点可以确定一个平面?
新知探究
存在性
唯一性
如何将这一基本事实用图形表示?
平面
如何用符号表示点和直线、平面的位置关系?
直线、平面都可以看成是无数个点组成的集合,
故点与直线、点与平面的关系是元素与集合的关系,
用“”或“”表示.
如图,点在直线上,记作; 点在直线外,记作;
点在平面内,记作;点在平面外,记作.
基本事实1:过不在一条直线的三个点,有且只有一个平面.
新知探究
你能举出一些生活实例来验证基本事实1吗?
基本事实1:过不在一条直线的三个点,有且只有一个平面.
自行车用一个脚架和两个车轮着地就可以“站稳”;
三脚架的三脚着地就可以支撑照相机;
将教室的门的两个铰链看成两个点,门插销看成一个点,当插销插上时,门不再动了.
新知探究
如果直线与平面有一个公共点,直线是否在平面内?
如果直线与平面有两个公共点呢?
P
l
A
B
l
直线不在平面内
直线在平面内
基本事实2:如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内.
新知探究
基本事实2:如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内.
如何将这一基本事实用图形表示?
如何用符号表示直线和平面的位置关系?
A
B
l
直线、平面都可以看成是无数个点组成的集合,
故直线与平面的关系是集合与集合的关系,用“”或“”表示.
如图,直线上所有的点都在平面内,就说直线在平面内,记作;
否则,就说直线不在平面内,记作.
基本事实2也可以用符号表示为:,,且, .
给定不共线三点,,确定一个平面;
由基本事实2,直线,,都在平面内,
进而连接这三条直线上任意两点所得直线也都在平面内,
所有这些直线可以编织成一个“直线网”,这个“直线网”可以铺满平面.
组成这个“直线网”的直线的“直”和向各个方向无限延伸,说明了平面的“平”和“无限延展”.
新知探究
我们知道,平面具有“平”和“无限延展”的特征,而基本事实2反映了直线与平面的位置关系,我们能不能利用这种位置关系,用直线的“直”和“无限延伸”刻画平面的“平”和“无限延展”?
把三角尺的一个角立在课桌面上,三角尺所在平面与课桌面所在平面是否只相交于一点?为什么?
新知探究
平面是无限延展的,适当补出三角尺所在平面
两平面交于一条直线
不止一个公共点,这些公共点是共线的
你还能举出生活中其它平面与平面相交的例子吗?
教室相邻的两个墙面在地面的墙角处有一个公共点,这两个墙面相交于过这个点的一条直线等.
新知探究
基本事实3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
P
l
P,P
符号语言:
结合基本事实3,你能进一步说明平面的“平”和“无限延展”的特征吗?
基本事实3说明:如果两个平面有一个公共点,那么这两个平面一定相交于过这个公共点的一条直线.两个平面相交成一条直线的事实,可以让我们进一步认识了平面的“平”和“无限延展”.
基本事实1给出了确定一个平面的一种方法.利用基本事实1和基本事实2,再结合“两点确定一条直线”,你还可以得到一些确定一个平面的方法吗?
新知探究
(1)
A
B
C
a
b
a
(2)
P
(3)
b
a
A
B
C
如图(1),设点是直线外一点,在直线上任取两点和,
则由基本事实1,经过,,三点确定一个平面,
再由基本事实2,直线也在平面内,
因此平面经过直线和点,即一条直线和这条直线外一点确定一个平面.
A
B
C
新知探究
推论1:一条直线和该直线外一点确定一个平面;
推论2:两条相交直线确定一个平面;
推论3:两条平行直线确定一个平面确定一个平面;
基本事实1:过不在一条直线的三个点,有且只有一个平面.
确定平面的依据!
应用举例
用符号表示下列语句,并画出图形:
(1)点在平面内但在平面外,平面相交于直线;
(2)直线经过平面内一点,外一点;
(3)直线在平面内,也在平面内.
文字语言
符号语言
图形语言
转 化
转 化
解:(1),. (如图①)
(2),,,,.(如图②)
(3).(如图③)
A
l
①
A
B
a
②
③
应用举例
已知:,,,.
求证:直线,,共面.
A
l
B
C
D
因为直线与点可以确定平面,
所以只需证明,,都在平面内.
证明:因为,所以与可以确定平面(推论1).
因为,所以.
又,所以(基本事实2).
同理,,所以,,在同一平面内,即它们共面.
应用举例
如图,在长方体中,为棱的中点,画出由,,三点所确定的平面与长方体表面的交线.
因为点既在平面内又在平面内,
所以点在平面与平面的交线上.
同理,点在平面与平面的交线上.
因此,就是平面与平面的交线.
作法:连接,,,它们就是平面与长方体表面的交线.
A
B
C
D
A1
B1
C1
D1
P
课堂练习
判断正误,并说明理由:
(1)平面与平面相交,它们只有有限个公共点.
(2)一个点和一条直线确定一个平面.
(3)两两相交的三条直线确定一个平面.
(4)如果两个平面有三个不共线的公共点,那么这两个平面重合.
根据基本事实3,两平面交于一条直线,有无限个公共点.
根据推论1,只有当点在线外,才能确定一个平面,若点在线上,则确定无数个平面.
若交点不重合,则能确定一个平面,若交点重合,则可能确定三个平面.
若两平面平行,无公共点;若两平面相交,则交点共线.
课堂练习
下列推理错误的是( )
A.
B.,
C.
D.
根据点、线、面的位置关系确定即可
A选项,,可能,所以A选项推理错误.
B选项,根据基本事实2可知,B选项正确.
C选项,因为,所以所以,C选项正确.
D选项,显然正确.
A
课堂练习
如图,正四棱柱ABCD-A′B′C′D′中,过对角线AC′的截面为菱形AEC′F,试着画出截面AEC′F与底面ABCD的交线.
C
B
A
D
E
C′
D′
B′
A′
F
M
N
延长CB、C′E交于点M,
延长CD、C′F交于点N,
连接MN,
则平面C′MN即截面AEC′F,
故MN即所需画的交线.
课堂练习
若直线l与平面相交于点O,,且AC∥BD,则三点的位置关系是 .
共线
D
O
C
B
A
l
如图,∵AC∥BD
∴AC,BD确定一个平面,设为平面
则C,D,l均在平面内
∵点O在直线l上
∴点O在平面内
又点O,C,D在平面内
∴平面,相交于O,C,D所在直线(基本事实3)
故O,C,D三点共线
归纳总结
回顾本节课的探究过程,你学到了什么?
基本事实
基本事实1:过不在一条直线的三个点,有且只有一个平面.
基本事实2:如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内.
基本事实3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
推论1:一条直线和该直线外一点确定一个平面.
推论2:两条相交直线确定一个平面.
推论3:两条平行直线确定一个平面.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
