青岛版小学数学五年级下册第二单元质量调研卷(含答案)
文档属性
| 名称 | 青岛版小学数学五年级下册第二单元质量调研卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 824.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-10 10:07:13 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
青岛版小学数学
五年级下册第二单元质量调研卷
一、选择题(16分)
1.有5吨货物,7次运完,每次运这批货物的( )。
A. B. C.0.5吨 D.吨
2.的分母加上24,要使分数的值不变,分子应( )。
A.加上24 B.乘3 C.加上32 D.加上15
3.与相等的分数( )。
A.只有1个 B.只有2个 C.有无数个 D.没有
4.里面有2个,有( )个。
A.2 B.4 C.8 D.10
5.截至2017年9月,我国与74个国家及国际组织签署“一带一路”合作文件270多项,部分统计如下表,数量最多的是( )。
类别 科教文卫类 经贸合作类 产能与投资合作类 标准互认类
各类别占文件总数的几分之几
A.科教文卫类 B.经贸合作类
C.产能与投资合作类 D.标准互认类
6.下面分数中,分数单位最大的一个数是( )。
A. B. C. D.
7.育新小学有a名女生,b名男生,男生人数占全校学生总数的( )。
A. B. C. D.
8.有2吨货物,平均5次运完,每次运这批货物的( )。
A. B. C.吨 D.吨
二、填空题(31分)
9.在括号里填上最简分数。
60平方分米=( )平方米 300克=( )千克 40秒=( )分
10.在括号填上“>”“<”或“=”。
( ) ( ) 4.25( )
11.一个最简真分数,分子和分母都扩大到原来的4倍后,分子与分母的和是24,这个分数原来是( )。
12.( )÷32===( )(填小数)。
13.一个最简分数,若将它的分子加上2,则等于。这个分数可能是( ),分数的分母加上27,要使分数的大小不变,分子应( )。
14.把一根3米长的绳子平均剪成5段,每段是3米的( ),每段长( )米。
15.把5个同样大小的面包平均分给3个小朋友,每个小朋友分得这些面包的 ,分得个面包。
16.五年级一班有38名学生,其中男生有23人,男生人数占全班人数的( ),女生人数占全班人数的( )。
17.的分数单位是( ),它有( )个这样的分数单位,把这个数化成带分数是( )。
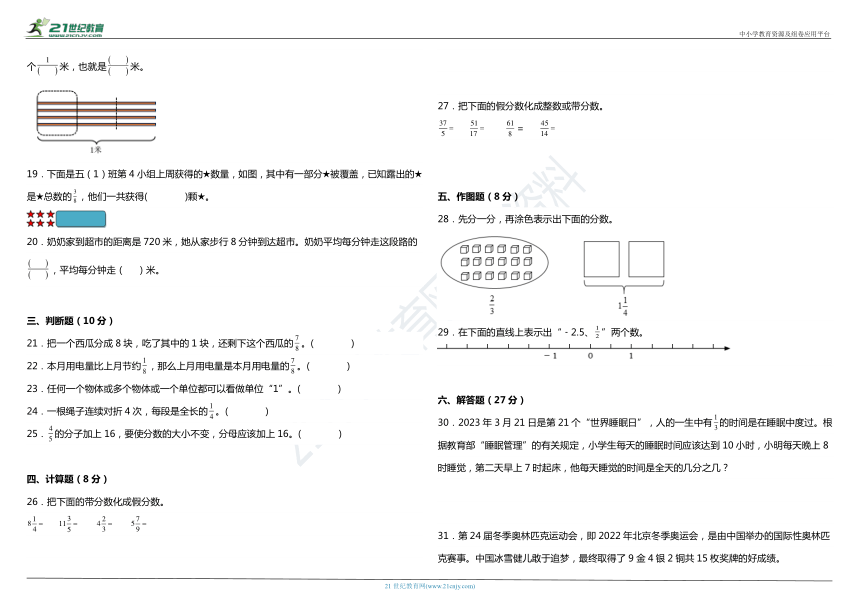
18.把4条1米长的绳子平均分成3份,拿走其中的1份(如图)。看图思考:拿走的是( )个米,也就是米。
19.下面是五(1)班第4小组上周获得的★数量,如图,其中有一部分★被覆盖,已知露出的★是★总数的,他们一共获得( )颗★。
20.奶奶家到超市的距离是720米,她从家步行8分钟到达超市。奶奶平均每分钟走这段路的,平均每分钟走( )米。
三、判断题(10分)
21.把一个西瓜分成8块,吃了其中的1块,还剩下这个西瓜的。( )
22.本月用电量比上月节约,那么上月用电量是本月用电量的。( )
23.任何一个物体或多个物体或一个单位都可以看做单位“1”。( )
24.一根绳子连续对折4次,每段是全长的。( )
25.的分子加上16,要使分数的大小不变,分母应该加上16。( )
四、计算题(8分)
26.把下面的带分数化成假分数。
27.把下面的假分数化成整数或带分数。
=
五、作图题(8分)
28.先分一分,再涂色表示出下面的分数。
29.在下面的直线上表示出“﹣2.5、”两个数。
六、解答题(27分)
30.2023年3月21日是第21个“世界睡眠日”,人的一生中有的时间是在睡眠中度过。根据教育部“睡眠管理”的有关规定,小学生每天的睡眠时间应该达到10小时,小明每天晚上8时睡觉,第二天早上7时起床,他每天睡觉的时间是全天的几分之几?
31.第24届冬季奥林匹克运动会,即2022年北京冬季奥运会,是由中国举办的国际性奥林匹克赛事。中国冰雪健儿敢于追梦,最终取得了9金4银2铜共15枚奖牌的好成绩。
(1)中国取得的金牌数占所获奖牌总数的几分之几?
(2)银牌和铜牌共占所获奖牌总数的几分之几?
(3)请根据所给出的数学信息提出一个数问题并解答。
32.王叔叔要用长3分米、宽2分米的瓷砖铺一个正方形图案。如果都用整块的瓷砖,铺成的图案边长至少是多少分米?(可以画图解决,也可以列式解决)
33.一根长米的铁丝。第一次剪去全长的,第二次剪去米,还剩下多少米?
34.一批货物共80吨,第一次运走了30吨,运走了总数的几分之几?还剩总数的几分之几?
有12个桃子,共重5千克,平均分给5只小猴子。每只小猴子分得桃子总数的几分之几?每只小猴子分到多少千克桃子?
参考答案:
1.B
【分析】将货物总吨数看作单位“1”,1÷运的次数=每次运这批货物的几分之几,据此列式计算。
【详解】1÷7=
每次运这批货物的。
故答案为:B
2.D
【分析】分数的分子和分母,同时乘或除以相同的数(0除外),分数的大小不变,据此分析。
【详解】(8+24)÷8
=32÷8
=4
5×4-5
=20-5
=15
的分母加上24,要使分数的值不变,分子应乘4或加上15。
故答案为:D
3.C
【分析】根据分数的基本性质,分子和分母同时乘或除以一个相同的数(0除外),分数的大小不变,据此解答即可。
【详解】由分析可得:与相等的分数有、、……,所以有无数个。
故答案为:C
4.C
【分析】这个分数的分子是2,就有2个分数单位。把这个分数化成分母是20的分数,然后根据分子确定分数单位的个数即可。
【详解】=
所以有8个。
故答案为:C
5.B
【分析】根据各类别占文件总数的分率,进行分数大小的比较即可解答。分母相同,分子越大,分数越大;异分母分数比较大小,可以先通分,再根据同分母分数比较大小的方法比较即可。
【详解】<<
=
>
所以数量最多的是经贸合作类。
故答案为:B
6.B
【分析】根据分数单位的意义,把单位“1”平均分成若干份,表示其中1份的数叫分数单位。分数比较大小:分子相同,分母较大的分数比较小,分母较小的分数比较大;所以分母越小,分数单位越大。
【详解】的分数单位是,的分数单位是,的分数单位是,的分数单位是;
<<<
所以分数单位最大的一个数是。
故答案为:B
【点睛】本题主要考查了分数单位的认识以及分数比较大小的方法。
7.D
【分析】已知育新小学的女生有a名、男生有b名,则全校共有学生(a+b)名,要求得男生人数占全校学生总数的几分之几;根据求一个数占另一个数的几分之几,用除法计算,列式为:b÷(a+b)。
【详解】b÷(a+b)=
男生人数占全校学生总数的。
故答案为:D
【点睛】考查了分数与除法的关系,分子相当于被除数、分母相当于除数;同时需要理清题目的数量关系。
8.B
【分析】将货物质量看作单位“1”,1÷运的次数=每次运这批货物的几分之几;货物质量÷运的次数=每次运的质量,据此分析。
【详解】1÷5=
2÷5=(吨)
每次运这批货物的,每次运吨。
故答案为:B
【点睛】关键是理解分数与除法的关系,分数的分子相当于被除数,分母相当于除数。
9.
【分析】根据1平方米=100平方分米,1千克=1000克,1分=60秒,单位小变大除以进率,分数的分子相当于被除数,分母相当于除数,据此用分数表示出换算结果,能约分的约分即可。
【详解】60÷100==(平方米);300÷1000==(千克);40÷60==(分)
60平方分米=平方米 300克=千克 40秒=分
10. > = <
【分析】异分母分数比较大小,先通分再比较。
带分数化假分数,分母不变,用分数部分的分母作分母,用分母和整数相乘的积再加上分数的的分子的和作为新分子。
分数化小数,直接用分子÷分母即可。
【详解】、,>
4×2+1=8+1=9,=
=18÷4=4.5,4.25<
11.
【分析】两个加数都扩大到原来的4倍,它们的和也会扩大到原来的4倍。分子和分母都扩大到原来的4倍后,分子与分母的和是24,则原来分子与分母的和是24÷4=6。
最简真分数的分子小于分母,且分子和分母是互质数。据此确定分数的分子和分母。
【详解】24÷4=6
6=1+5=2+4=3+3
1和5是互质数,则这个分数原来是。
12.28;64;0.875
【分析】分数的分子相当于被除数,分母相当于除数,分数的分子和分母,同时乘或除以相同的数(0除外),分数的大小不变。据此根据分数与除法的关系,以及它们通用的基本性质进行填空,分数化小数,直接用分子÷分母即可。
【详解】32÷8×7=28;56÷7×8=64;7÷8=0.875
28÷32===0.875
13. 、、……(答案不唯一) 乘4(答案不唯一)
【分析】根据分数的基本性质,分别给的分子和分母同时乘3、4、5、6……,根据题意,给分数的分子减去2即可求解。的分母加上27后得36,是9乘4得到的,根据分数的基本性质,分子也要乘4
【详解】……
则有:是最简分数,符合题意;
不是最简分数,不符合题意;
是最简分数,符合题意;
不是最简分数,不符合题意;
是最简分数,符合题意;
……一个最简分数,若将它的分子加上2,则等于。这个分数可能是:、、……(答案不唯一)
分数的分母加上27,要使分数的大小不变,分子应乘4。(答案不唯一)
【点睛】灵活运用分数的基本性质是解答本题的关键。
14. /0.6
【分析】求每段是3米的几分之几,是把这根绳子的全长看作单位“1”,把“1”平均分成5段,用1除以5;
求每段的长度,是把3米长的绳子平均分成5段,用这根绳子的长度除以5。
【详解】1÷5=
3÷5=(米)
每段是3米的,每段长米。
【点睛】解决此题关键是弄清求的是“分率”还是“具体的数量”,求分率,平均分的是单位“1”;求具体的数量,平均分的是具体的数量。注意:分率不带单位名称,而具体的数量要带单位名称。
15.;
【分析】求每个小朋友分得这些面包的几分之几,是把面包的总个数看作单位“1”,把“1”平均分给3个小朋友,用1除以3;
求每个小朋友分得面包的个数,是把5个面包平均分给3个小朋友,用面包的总个数除以3。
【详解】1÷3=
5÷3=(个)
每个小朋友分得这些面包的,分得个面包。
【点睛】解决此题关键是弄清求的是“分率”还是“具体的数量”,求分率,平均分的是单位“1”;求具体的数量,平均分的是具体的数量。注意:分率不带单位名称,而具体的数量要带单位名称。
16.
【分析】五年级一班有38名学生,其中男生有23人,则要求得男生人数占全班人数的几分之几,列式为:23÷38;再求得女生人数为38-23=15(人),则女生人数占全班人数的15÷38;结果用分数表示。
【详解】23÷38=
38-23=15(人)
15÷38=
五年级一班有38名学生,其中男生有23人,男生人数占全班人数的(),女生人数占全班人数的()。
【点睛】考查了分数与除法的关系,需要明确是求哪个量占哪个量的几分之几,对应好数据,再列式。
17. 16
【分析】一个分数的分母是几,分数单位就是几分之一;
分子是几,就有几个分数单位;
把假分数化成整数或带分数:用分子÷分母。能整除的,所得的商就是整数;不能整除的,所得的商就是带分数的整数部分,余数是就是分数部分的分子,分母不变。
【详解】=16÷7=
的分数单位是,它有16个这样的分数单位,化成带分数是。
【点睛】考查了对于分数单位的理解,同时需要熟练掌握假分数带分数的互化。
18.4;;
【分析】根据分数的意义,把1米长的绳子看作单位“1”,把绳子平均分成3份,每份是米;如果是把4条1米长的绳子平均分成3份,则每份是4个米,也就是米。
【详解】把4条1米长的绳子平均分成3份,拿走其中的1份;拿走的是4个米,也就是米。
【点睛】本题主要考查了分数的意义,明确分数带单位和不带单位的区别。
19.16
【分析】分数的意义:把单位“1”平均分成若干份,表示其中一份或几份的数;根据分数的意义,可知表示把星星数量看作单位“1”,平均分成8份,露出的部分占3份,已知露出了6颗,用6÷3即可求出每份是多少颗,再乘8即可求出星星的总数量。
【详解】6÷3×8=16(颗)
他们一共获得16颗星星。
【点睛】解决此题明确分数的分母表示把单位“1”平均分成的份数,分子表示被涂色的份数。
20.;90
【分析】把720米看作单位“1”,平均分成8份,1分钟走这样的1份,求奶奶平均每分钟走这段路的几分之几,即是求1份占8份的几分之几。求一个数是另一个数(0除外)的几分之几的解题方法:一个数÷另一个数=。据此用1÷8可求出奶奶平均每分钟走这段路的几分之几。
根据路程÷时间=速度,用720÷8可求出奶奶平均每分钟走的米数。
【详解】1÷8=
720÷8=90(米)
所以奶奶平均每分钟走这段路的,平均每分钟走90米。
【点睛】此题考查了求一个数是另一个数的几分之几的问题、分数与除法的关系、行程问题的数量关系。
21.×
【分析】把一个物体平均分成几份,表示其中的一份或几份的数,叫做分数,据此即可解答。
【详解】西瓜分成8块,因为不是平均分8块,无法确定1块西瓜占整个西瓜的分率,也就无法求出剩下部分占这个西瓜的分率。
原题干说法错误。
故答案为:×
22.×
【分析】根据本月用电量比上月节约,可以将上月用电量看作8,本月用电量看作(8-1),上月用电量÷本月用电量=上月用电量是本月用电量的几分之几。
【详解】8÷(8-1)
=8÷7
=
本月用电量比上月节约,那么上月用电量是本月用电量的,所以原题说法错误。
故答案为:×
23.√
【分析】一个物体、一个计量单位或是一些物体等组成的一个整体都可以看作单位“1”;据此判断。
【详解】任何一个物体或多个物体或一个单位都可以看做单位“1”。
原题说法正确。
故答案为:√
【点睛】本题考查单位“1”的认识。
24.×
【分析】如果把这根绳子对折1次,就把它平均分成2段,每段是;对折2次,平均分成4段,每段是;对折3次,平均分成8段,每段是;对折4次,平均分成16段,每段是全长的。据此解答。
【详解】一根绳子,连续对折4次,平均分成了24=2×2×2×2=16(段),每段是全长的。原题说法错误。
故答案为:×
【点睛】需要理解绳子对折的规律,对折n次,平均分成2n段;要求得分段是全长的几分之几,就用1除以段数。
25.×
【分析】把的分子加上16后,分子变为20,相当于分子乘5,根据分数的基本性质,分数的分子、分母同时乘或除以同一个不为0的数,分数的大小不变;所以要使分数的大小不变,分母也应该乘5,这时分母变为25,再减去原来的数5,即可得到分母应增加的数。
【详解】4+16=20
20÷4=5
所以分母也应该乘5。
或者增加:
5×5-5
=25-5
=20
即分母应该加20。
故答案为:×
【点睛】此题的解题关键是灵活运用分数的基本性质求解。
26.;;;
【分析】带分数化假分数:分母不变,用分数部分的分母作分母,用分母和整数相乘的积,再加上分数的分子的和作为新分子,据此解答即可。
【详解】;
;
;
。
【点睛】掌握带分数与假分数的换算方法是解题的关键
27.;3;;
【分析】用分子除以分母。当分子是分母的整数倍时,能化成整数,商就是这个整数。当分子不是分母的整数倍时,能化成带分数,商是带分数的整数部分,余数是分数部分的分子,分母不变。
【详解】37÷5=7……2,
51÷17=3,3
61÷8=7……5,=
45÷14=3……3,
28.见详解
【分析】分数的意义,把单位“1”平均分成若干份,表示这样的一份或几份的数叫做分数。分母是平均分的总份数,分子是取的其中的几份。
左图,把这些小正方体看作单位“1”,把它平均分成3份,取其中的2份涂色,用分数表示为。
右图,把一个正方形看作单位“1”,图中共有两个相同的正方形,其中1个正方形全部涂色,用“1”表示;第2个正方形平均分成了4份,取其中的一份涂色,用分数表示为“”;涂色部分合起来用分数表示为。
【详解】如图:
(答案不唯一)
【点睛】掌握分数的意义是解题的关键。
29.见详解
【分析】在数轴上表示数的时候,原点0的左边是负数,右边是正数,图中0~1之间有两小格,根据分数的意义,把这段长度看作单位“1”,平均分成2份,其中1份用分数即可表示;同时也表示每小格代表,化成小数是0.5,那么﹣2.5应该从0开始往左边数,第5小格的位置,即可表示“﹣2.5”。据此解答。
【详解】如图:
【点睛】此题主要考查正负数在数轴上的表示,理解数轴表示数的方法,正数在0的右边,负数在0的左边。
30.
【分析】求得晚上8时到第二天早上7时共睡觉的时间,以全天24小时为单位“1”,根据分数的意义,用睡觉的时间除以24,即得到睡觉的时间是全天的几分之几,据此解答。
【详解】晚八时到第二天早上七时共睡觉的时间:
12:00-8:00=4(小时)
7:00-0:00=7(小时)
7+4=11(小时)
11÷24=
答:他每天睡觉的时间是全天的。
31.(1)
(2)
(3)银牌数占所获奖牌总数的几分之几?
【分析】(1)中国取得的金牌数÷所获奖牌总数=中国取得的金牌数占所获奖牌总数的几分之几。
(2)(银牌数+铜牌数)÷所获奖牌总数=银牌和铜牌共占所获奖牌总数的几分之。
(3)答案不唯一,如银牌数占所获奖牌总数的几分之几?银牌数÷所获奖牌总数=银牌数占所获奖牌总数的几分之几。
【详解】(1)9÷15==
答:中国取得的金牌数占所获奖牌总数的。
(2)(4+2)÷15
=6÷15
=
=
答:银牌和铜牌共占所获奖牌总数的。
(3)银牌数占所获奖牌总数的几分之几?
4÷15=
答:银牌数占所获奖牌总数的。
32.6分米
【分析】由分析可知,要用长3分米、宽2分米的瓷砖铺一个正方形图案,实际上就是求出2和3的最小公倍数;2和3是互质数,所以两个数的最小公倍数是两个数的乘积。
【详解】2×3=6(分米)
答:铺成的图案边长至少是6分米。
【点睛】本题考查公倍数的计算及应用,理解题意,找出最小公倍数是解决本题的关键。
33.0.33米
【分析】先把米化成小数是0.7米,米化成小数是0.3米。全长的是把这根铁丝的全长看作单位“1”平均分成10份,取这样的1份,即第一次剪去的米数是0.7÷10=0.07(米)。用全长0.7米减去0.07米,再减去0.3米,即可求出剩下的米数。
【详解】米=0.7米
米=0.3米
0.7-0.7÷10-0.3
=0.7-0.07-0.3
=0.63-0.3
=0.33(米)
答:还剩下0.33米。
【点睛】此题考查了分数的意义、分数化小数。另外还需要注意数量与分率的区别,米和米是数量,是分率。
34.;
【分析】用30÷80即可求出运走的占总数的几分之几;运走30吨,还剩下80-30=50吨,用50÷80即可求出剩下的占总数的几分之几。
【详解】30÷80=
(80-30)÷80
=50÷80
=
答:运走了总数的,还剩下总数的。
【点睛】此题考查求一个数占另一个数几分之几的求法以及分数与除法的关系的应用。
35.;1千克
【分析】求每只小猴子分得桃子总数的几分之几,平均分的是单位“1”,表示把单位“1”平均分成5份,求的是每一份占的分率,用除法计算。把桃子的总重量5千克平均分成5只小猴子,可用除法算出每只小猴子分到多少千克桃子。
【详解】1÷5=
5÷5=1(千克)
答:每只小猴子分得桃子总数的,每只小猴子分到1千克桃子。
【点睛】解决此题关键是弄清求得是分率还是具体的数量,求分率平均分的是单位“1”,求具体的数量平均分的是具体的数量,要注意分率不能带单位名称,而具体的数量要带单位名称。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
青岛版小学数学
五年级下册第二单元质量调研卷
一、选择题(16分)
1.有5吨货物,7次运完,每次运这批货物的( )。
A. B. C.0.5吨 D.吨
2.的分母加上24,要使分数的值不变,分子应( )。
A.加上24 B.乘3 C.加上32 D.加上15
3.与相等的分数( )。
A.只有1个 B.只有2个 C.有无数个 D.没有
4.里面有2个,有( )个。
A.2 B.4 C.8 D.10
5.截至2017年9月,我国与74个国家及国际组织签署“一带一路”合作文件270多项,部分统计如下表,数量最多的是( )。
类别 科教文卫类 经贸合作类 产能与投资合作类 标准互认类
各类别占文件总数的几分之几
A.科教文卫类 B.经贸合作类
C.产能与投资合作类 D.标准互认类
6.下面分数中,分数单位最大的一个数是( )。
A. B. C. D.
7.育新小学有a名女生,b名男生,男生人数占全校学生总数的( )。
A. B. C. D.
8.有2吨货物,平均5次运完,每次运这批货物的( )。
A. B. C.吨 D.吨
二、填空题(31分)
9.在括号里填上最简分数。
60平方分米=( )平方米 300克=( )千克 40秒=( )分
10.在括号填上“>”“<”或“=”。
( ) ( ) 4.25( )
11.一个最简真分数,分子和分母都扩大到原来的4倍后,分子与分母的和是24,这个分数原来是( )。
12.( )÷32===( )(填小数)。
13.一个最简分数,若将它的分子加上2,则等于。这个分数可能是( ),分数的分母加上27,要使分数的大小不变,分子应( )。
14.把一根3米长的绳子平均剪成5段,每段是3米的( ),每段长( )米。
15.把5个同样大小的面包平均分给3个小朋友,每个小朋友分得这些面包的 ,分得个面包。
16.五年级一班有38名学生,其中男生有23人,男生人数占全班人数的( ),女生人数占全班人数的( )。
17.的分数单位是( ),它有( )个这样的分数单位,把这个数化成带分数是( )。
18.把4条1米长的绳子平均分成3份,拿走其中的1份(如图)。看图思考:拿走的是( )个米,也就是米。
19.下面是五(1)班第4小组上周获得的★数量,如图,其中有一部分★被覆盖,已知露出的★是★总数的,他们一共获得( )颗★。
20.奶奶家到超市的距离是720米,她从家步行8分钟到达超市。奶奶平均每分钟走这段路的,平均每分钟走( )米。
三、判断题(10分)
21.把一个西瓜分成8块,吃了其中的1块,还剩下这个西瓜的。( )
22.本月用电量比上月节约,那么上月用电量是本月用电量的。( )
23.任何一个物体或多个物体或一个单位都可以看做单位“1”。( )
24.一根绳子连续对折4次,每段是全长的。( )
25.的分子加上16,要使分数的大小不变,分母应该加上16。( )
四、计算题(8分)
26.把下面的带分数化成假分数。
27.把下面的假分数化成整数或带分数。
=
五、作图题(8分)
28.先分一分,再涂色表示出下面的分数。
29.在下面的直线上表示出“﹣2.5、”两个数。
六、解答题(27分)
30.2023年3月21日是第21个“世界睡眠日”,人的一生中有的时间是在睡眠中度过。根据教育部“睡眠管理”的有关规定,小学生每天的睡眠时间应该达到10小时,小明每天晚上8时睡觉,第二天早上7时起床,他每天睡觉的时间是全天的几分之几?
31.第24届冬季奥林匹克运动会,即2022年北京冬季奥运会,是由中国举办的国际性奥林匹克赛事。中国冰雪健儿敢于追梦,最终取得了9金4银2铜共15枚奖牌的好成绩。
(1)中国取得的金牌数占所获奖牌总数的几分之几?
(2)银牌和铜牌共占所获奖牌总数的几分之几?
(3)请根据所给出的数学信息提出一个数问题并解答。
32.王叔叔要用长3分米、宽2分米的瓷砖铺一个正方形图案。如果都用整块的瓷砖,铺成的图案边长至少是多少分米?(可以画图解决,也可以列式解决)
33.一根长米的铁丝。第一次剪去全长的,第二次剪去米,还剩下多少米?
34.一批货物共80吨,第一次运走了30吨,运走了总数的几分之几?还剩总数的几分之几?
有12个桃子,共重5千克,平均分给5只小猴子。每只小猴子分得桃子总数的几分之几?每只小猴子分到多少千克桃子?
参考答案:
1.B
【分析】将货物总吨数看作单位“1”,1÷运的次数=每次运这批货物的几分之几,据此列式计算。
【详解】1÷7=
每次运这批货物的。
故答案为:B
2.D
【分析】分数的分子和分母,同时乘或除以相同的数(0除外),分数的大小不变,据此分析。
【详解】(8+24)÷8
=32÷8
=4
5×4-5
=20-5
=15
的分母加上24,要使分数的值不变,分子应乘4或加上15。
故答案为:D
3.C
【分析】根据分数的基本性质,分子和分母同时乘或除以一个相同的数(0除外),分数的大小不变,据此解答即可。
【详解】由分析可得:与相等的分数有、、……,所以有无数个。
故答案为:C
4.C
【分析】这个分数的分子是2,就有2个分数单位。把这个分数化成分母是20的分数,然后根据分子确定分数单位的个数即可。
【详解】=
所以有8个。
故答案为:C
5.B
【分析】根据各类别占文件总数的分率,进行分数大小的比较即可解答。分母相同,分子越大,分数越大;异分母分数比较大小,可以先通分,再根据同分母分数比较大小的方法比较即可。
【详解】<<
=
>
所以数量最多的是经贸合作类。
故答案为:B
6.B
【分析】根据分数单位的意义,把单位“1”平均分成若干份,表示其中1份的数叫分数单位。分数比较大小:分子相同,分母较大的分数比较小,分母较小的分数比较大;所以分母越小,分数单位越大。
【详解】的分数单位是,的分数单位是,的分数单位是,的分数单位是;
<<<
所以分数单位最大的一个数是。
故答案为:B
【点睛】本题主要考查了分数单位的认识以及分数比较大小的方法。
7.D
【分析】已知育新小学的女生有a名、男生有b名,则全校共有学生(a+b)名,要求得男生人数占全校学生总数的几分之几;根据求一个数占另一个数的几分之几,用除法计算,列式为:b÷(a+b)。
【详解】b÷(a+b)=
男生人数占全校学生总数的。
故答案为:D
【点睛】考查了分数与除法的关系,分子相当于被除数、分母相当于除数;同时需要理清题目的数量关系。
8.B
【分析】将货物质量看作单位“1”,1÷运的次数=每次运这批货物的几分之几;货物质量÷运的次数=每次运的质量,据此分析。
【详解】1÷5=
2÷5=(吨)
每次运这批货物的,每次运吨。
故答案为:B
【点睛】关键是理解分数与除法的关系,分数的分子相当于被除数,分母相当于除数。
9.
【分析】根据1平方米=100平方分米,1千克=1000克,1分=60秒,单位小变大除以进率,分数的分子相当于被除数,分母相当于除数,据此用分数表示出换算结果,能约分的约分即可。
【详解】60÷100==(平方米);300÷1000==(千克);40÷60==(分)
60平方分米=平方米 300克=千克 40秒=分
10. > = <
【分析】异分母分数比较大小,先通分再比较。
带分数化假分数,分母不变,用分数部分的分母作分母,用分母和整数相乘的积再加上分数的的分子的和作为新分子。
分数化小数,直接用分子÷分母即可。
【详解】、,>
4×2+1=8+1=9,=
=18÷4=4.5,4.25<
11.
【分析】两个加数都扩大到原来的4倍,它们的和也会扩大到原来的4倍。分子和分母都扩大到原来的4倍后,分子与分母的和是24,则原来分子与分母的和是24÷4=6。
最简真分数的分子小于分母,且分子和分母是互质数。据此确定分数的分子和分母。
【详解】24÷4=6
6=1+5=2+4=3+3
1和5是互质数,则这个分数原来是。
12.28;64;0.875
【分析】分数的分子相当于被除数,分母相当于除数,分数的分子和分母,同时乘或除以相同的数(0除外),分数的大小不变。据此根据分数与除法的关系,以及它们通用的基本性质进行填空,分数化小数,直接用分子÷分母即可。
【详解】32÷8×7=28;56÷7×8=64;7÷8=0.875
28÷32===0.875
13. 、、……(答案不唯一) 乘4(答案不唯一)
【分析】根据分数的基本性质,分别给的分子和分母同时乘3、4、5、6……,根据题意,给分数的分子减去2即可求解。的分母加上27后得36,是9乘4得到的,根据分数的基本性质,分子也要乘4
【详解】……
则有:是最简分数,符合题意;
不是最简分数,不符合题意;
是最简分数,符合题意;
不是最简分数,不符合题意;
是最简分数,符合题意;
……一个最简分数,若将它的分子加上2,则等于。这个分数可能是:、、……(答案不唯一)
分数的分母加上27,要使分数的大小不变,分子应乘4。(答案不唯一)
【点睛】灵活运用分数的基本性质是解答本题的关键。
14. /0.6
【分析】求每段是3米的几分之几,是把这根绳子的全长看作单位“1”,把“1”平均分成5段,用1除以5;
求每段的长度,是把3米长的绳子平均分成5段,用这根绳子的长度除以5。
【详解】1÷5=
3÷5=(米)
每段是3米的,每段长米。
【点睛】解决此题关键是弄清求的是“分率”还是“具体的数量”,求分率,平均分的是单位“1”;求具体的数量,平均分的是具体的数量。注意:分率不带单位名称,而具体的数量要带单位名称。
15.;
【分析】求每个小朋友分得这些面包的几分之几,是把面包的总个数看作单位“1”,把“1”平均分给3个小朋友,用1除以3;
求每个小朋友分得面包的个数,是把5个面包平均分给3个小朋友,用面包的总个数除以3。
【详解】1÷3=
5÷3=(个)
每个小朋友分得这些面包的,分得个面包。
【点睛】解决此题关键是弄清求的是“分率”还是“具体的数量”,求分率,平均分的是单位“1”;求具体的数量,平均分的是具体的数量。注意:分率不带单位名称,而具体的数量要带单位名称。
16.
【分析】五年级一班有38名学生,其中男生有23人,则要求得男生人数占全班人数的几分之几,列式为:23÷38;再求得女生人数为38-23=15(人),则女生人数占全班人数的15÷38;结果用分数表示。
【详解】23÷38=
38-23=15(人)
15÷38=
五年级一班有38名学生,其中男生有23人,男生人数占全班人数的(),女生人数占全班人数的()。
【点睛】考查了分数与除法的关系,需要明确是求哪个量占哪个量的几分之几,对应好数据,再列式。
17. 16
【分析】一个分数的分母是几,分数单位就是几分之一;
分子是几,就有几个分数单位;
把假分数化成整数或带分数:用分子÷分母。能整除的,所得的商就是整数;不能整除的,所得的商就是带分数的整数部分,余数是就是分数部分的分子,分母不变。
【详解】=16÷7=
的分数单位是,它有16个这样的分数单位,化成带分数是。
【点睛】考查了对于分数单位的理解,同时需要熟练掌握假分数带分数的互化。
18.4;;
【分析】根据分数的意义,把1米长的绳子看作单位“1”,把绳子平均分成3份,每份是米;如果是把4条1米长的绳子平均分成3份,则每份是4个米,也就是米。
【详解】把4条1米长的绳子平均分成3份,拿走其中的1份;拿走的是4个米,也就是米。
【点睛】本题主要考查了分数的意义,明确分数带单位和不带单位的区别。
19.16
【分析】分数的意义:把单位“1”平均分成若干份,表示其中一份或几份的数;根据分数的意义,可知表示把星星数量看作单位“1”,平均分成8份,露出的部分占3份,已知露出了6颗,用6÷3即可求出每份是多少颗,再乘8即可求出星星的总数量。
【详解】6÷3×8=16(颗)
他们一共获得16颗星星。
【点睛】解决此题明确分数的分母表示把单位“1”平均分成的份数,分子表示被涂色的份数。
20.;90
【分析】把720米看作单位“1”,平均分成8份,1分钟走这样的1份,求奶奶平均每分钟走这段路的几分之几,即是求1份占8份的几分之几。求一个数是另一个数(0除外)的几分之几的解题方法:一个数÷另一个数=。据此用1÷8可求出奶奶平均每分钟走这段路的几分之几。
根据路程÷时间=速度,用720÷8可求出奶奶平均每分钟走的米数。
【详解】1÷8=
720÷8=90(米)
所以奶奶平均每分钟走这段路的,平均每分钟走90米。
【点睛】此题考查了求一个数是另一个数的几分之几的问题、分数与除法的关系、行程问题的数量关系。
21.×
【分析】把一个物体平均分成几份,表示其中的一份或几份的数,叫做分数,据此即可解答。
【详解】西瓜分成8块,因为不是平均分8块,无法确定1块西瓜占整个西瓜的分率,也就无法求出剩下部分占这个西瓜的分率。
原题干说法错误。
故答案为:×
22.×
【分析】根据本月用电量比上月节约,可以将上月用电量看作8,本月用电量看作(8-1),上月用电量÷本月用电量=上月用电量是本月用电量的几分之几。
【详解】8÷(8-1)
=8÷7
=
本月用电量比上月节约,那么上月用电量是本月用电量的,所以原题说法错误。
故答案为:×
23.√
【分析】一个物体、一个计量单位或是一些物体等组成的一个整体都可以看作单位“1”;据此判断。
【详解】任何一个物体或多个物体或一个单位都可以看做单位“1”。
原题说法正确。
故答案为:√
【点睛】本题考查单位“1”的认识。
24.×
【分析】如果把这根绳子对折1次,就把它平均分成2段,每段是;对折2次,平均分成4段,每段是;对折3次,平均分成8段,每段是;对折4次,平均分成16段,每段是全长的。据此解答。
【详解】一根绳子,连续对折4次,平均分成了24=2×2×2×2=16(段),每段是全长的。原题说法错误。
故答案为:×
【点睛】需要理解绳子对折的规律,对折n次,平均分成2n段;要求得分段是全长的几分之几,就用1除以段数。
25.×
【分析】把的分子加上16后,分子变为20,相当于分子乘5,根据分数的基本性质,分数的分子、分母同时乘或除以同一个不为0的数,分数的大小不变;所以要使分数的大小不变,分母也应该乘5,这时分母变为25,再减去原来的数5,即可得到分母应增加的数。
【详解】4+16=20
20÷4=5
所以分母也应该乘5。
或者增加:
5×5-5
=25-5
=20
即分母应该加20。
故答案为:×
【点睛】此题的解题关键是灵活运用分数的基本性质求解。
26.;;;
【分析】带分数化假分数:分母不变,用分数部分的分母作分母,用分母和整数相乘的积,再加上分数的分子的和作为新分子,据此解答即可。
【详解】;
;
;
。
【点睛】掌握带分数与假分数的换算方法是解题的关键
27.;3;;
【分析】用分子除以分母。当分子是分母的整数倍时,能化成整数,商就是这个整数。当分子不是分母的整数倍时,能化成带分数,商是带分数的整数部分,余数是分数部分的分子,分母不变。
【详解】37÷5=7……2,
51÷17=3,3
61÷8=7……5,=
45÷14=3……3,
28.见详解
【分析】分数的意义,把单位“1”平均分成若干份,表示这样的一份或几份的数叫做分数。分母是平均分的总份数,分子是取的其中的几份。
左图,把这些小正方体看作单位“1”,把它平均分成3份,取其中的2份涂色,用分数表示为。
右图,把一个正方形看作单位“1”,图中共有两个相同的正方形,其中1个正方形全部涂色,用“1”表示;第2个正方形平均分成了4份,取其中的一份涂色,用分数表示为“”;涂色部分合起来用分数表示为。
【详解】如图:
(答案不唯一)
【点睛】掌握分数的意义是解题的关键。
29.见详解
【分析】在数轴上表示数的时候,原点0的左边是负数,右边是正数,图中0~1之间有两小格,根据分数的意义,把这段长度看作单位“1”,平均分成2份,其中1份用分数即可表示;同时也表示每小格代表,化成小数是0.5,那么﹣2.5应该从0开始往左边数,第5小格的位置,即可表示“﹣2.5”。据此解答。
【详解】如图:
【点睛】此题主要考查正负数在数轴上的表示,理解数轴表示数的方法,正数在0的右边,负数在0的左边。
30.
【分析】求得晚上8时到第二天早上7时共睡觉的时间,以全天24小时为单位“1”,根据分数的意义,用睡觉的时间除以24,即得到睡觉的时间是全天的几分之几,据此解答。
【详解】晚八时到第二天早上七时共睡觉的时间:
12:00-8:00=4(小时)
7:00-0:00=7(小时)
7+4=11(小时)
11÷24=
答:他每天睡觉的时间是全天的。
31.(1)
(2)
(3)银牌数占所获奖牌总数的几分之几?
【分析】(1)中国取得的金牌数÷所获奖牌总数=中国取得的金牌数占所获奖牌总数的几分之几。
(2)(银牌数+铜牌数)÷所获奖牌总数=银牌和铜牌共占所获奖牌总数的几分之。
(3)答案不唯一,如银牌数占所获奖牌总数的几分之几?银牌数÷所获奖牌总数=银牌数占所获奖牌总数的几分之几。
【详解】(1)9÷15==
答:中国取得的金牌数占所获奖牌总数的。
(2)(4+2)÷15
=6÷15
=
=
答:银牌和铜牌共占所获奖牌总数的。
(3)银牌数占所获奖牌总数的几分之几?
4÷15=
答:银牌数占所获奖牌总数的。
32.6分米
【分析】由分析可知,要用长3分米、宽2分米的瓷砖铺一个正方形图案,实际上就是求出2和3的最小公倍数;2和3是互质数,所以两个数的最小公倍数是两个数的乘积。
【详解】2×3=6(分米)
答:铺成的图案边长至少是6分米。
【点睛】本题考查公倍数的计算及应用,理解题意,找出最小公倍数是解决本题的关键。
33.0.33米
【分析】先把米化成小数是0.7米,米化成小数是0.3米。全长的是把这根铁丝的全长看作单位“1”平均分成10份,取这样的1份,即第一次剪去的米数是0.7÷10=0.07(米)。用全长0.7米减去0.07米,再减去0.3米,即可求出剩下的米数。
【详解】米=0.7米
米=0.3米
0.7-0.7÷10-0.3
=0.7-0.07-0.3
=0.63-0.3
=0.33(米)
答:还剩下0.33米。
【点睛】此题考查了分数的意义、分数化小数。另外还需要注意数量与分率的区别,米和米是数量,是分率。
34.;
【分析】用30÷80即可求出运走的占总数的几分之几;运走30吨,还剩下80-30=50吨,用50÷80即可求出剩下的占总数的几分之几。
【详解】30÷80=
(80-30)÷80
=50÷80
=
答:运走了总数的,还剩下总数的。
【点睛】此题考查求一个数占另一个数几分之几的求法以及分数与除法的关系的应用。
35.;1千克
【分析】求每只小猴子分得桃子总数的几分之几,平均分的是单位“1”,表示把单位“1”平均分成5份,求的是每一份占的分率,用除法计算。把桃子的总重量5千克平均分成5只小猴子,可用除法算出每只小猴子分到多少千克桃子。
【详解】1÷5=
5÷5=1(千克)
答:每只小猴子分得桃子总数的,每只小猴子分到1千克桃子。
【点睛】解决此题关键是弄清求得是分率还是具体的数量,求分率平均分的是单位“1”,求具体的数量平均分的是具体的数量,要注意分率不能带单位名称,而具体的数量要带单位名称。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
