人教版八年级下册17.1.2 勾股定理的实际应用 同步练习(含答案)
文档属性
| 名称 | 人教版八年级下册17.1.2 勾股定理的实际应用 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 150.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-09 19:21:15 | ||
图片预览


文档简介
第十七章 勾股定理
17.1 勾股定理
第2课时 勾股定理的实际应用
一、选择题
1.一只蚂蚁在水平地面上朝正东方向爬行12 cm,再朝正南方向爬行16 cm,这时它离出发点的距离为( )
A.15 cm B.18 cm C.20 cm D.28 cm
2.如图,湖的两岸有A,B两点,在与AB垂直的BC方向上的点C处测得AC=50米,BC=30米,则A,B两点间的距离为( )
A.40米 B.30米
C.50米 D.10米
3.在同一水平面上有两棵树,一棵树高10 m,另一棵树高4 m,两树相距8 m.一只小鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少要飞行( )
A.8 m B.10 m C.12 m D.14 m
4.如图,为了测算出学校旗杆的高度,小明将升旗的绳子拉到旗杆底端,并在与旗杆等长的地方打了一个结,然后将绳子底端拉到离旗杆底端5米的地面某处,发现此时绳子底端距离打结处1米,则旗杆的高度是( )
A.12米 B.13米 C.15米 D.24米
5.如图是一扇高为2 m、宽为1.5 m的门框.李师傅有3块薄木板,尺寸如下:①号木板长3 m,宽2.7 m;②号木板长2.8 m,宽2.8 m;③号木板长4 m,宽2.4 m.可以从这扇门通过的木板是( )
A.①号 B.②号C.③号 D.均不能通过
二、填空题
6.如果梯子的底端离建筑物9米,那么15米长的梯子可以到达的建筑物的高度是 米.
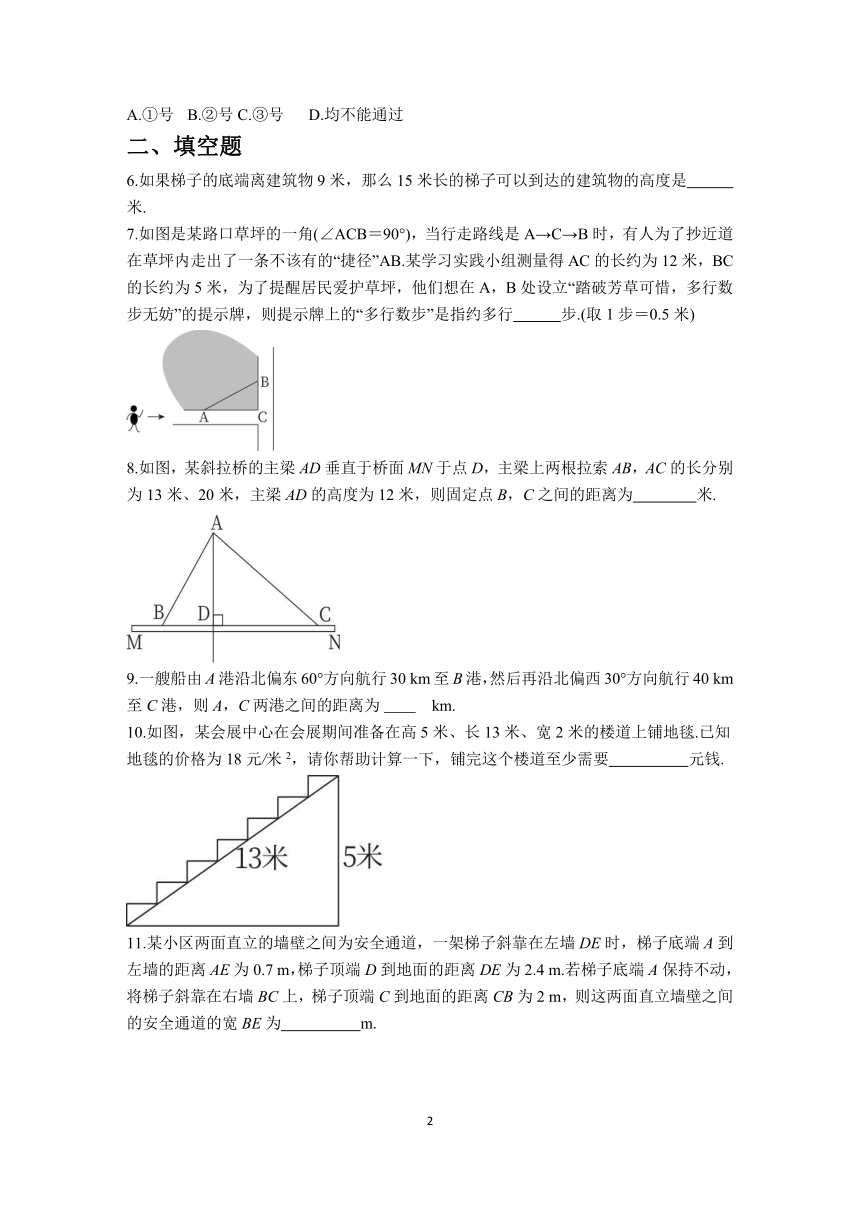
7.如图是某路口草坪的一角(∠ACB=90°),当行走路线是A→C→B时,有人为了抄近道在草坪内走出了一条不该有的“捷径”AB.某学习实践小组测量得AC的长约为12米,BC的长约为5米,为了提醒居民爱护草坪,他们想在A,B处设立“踏破芳草可惜,多行数步无妨”的提示牌,则提示牌上的“多行数步”是指约多行 步.(取1步=0.5米)
8.如图,某斜拉桥的主梁AD垂直于桥面MN于点D,主梁上两根拉索AB,AC的长分别为13米、20米,主梁AD的高度为12米,则固定点B,C之间的距离为 米.
9.一艘船由A港沿北偏东60°方向航行30 km至B港,然后再沿北偏西30°方向航行40 km至C港,则A,C两港之间的距离为 km.
10.如图,某会展中心在会展期间准备在高5米、长13米、宽2米的楼道上铺地毯.已知地毯的价格为18元/米2,请你帮助计算一下,铺完这个楼道至少需要 元钱.
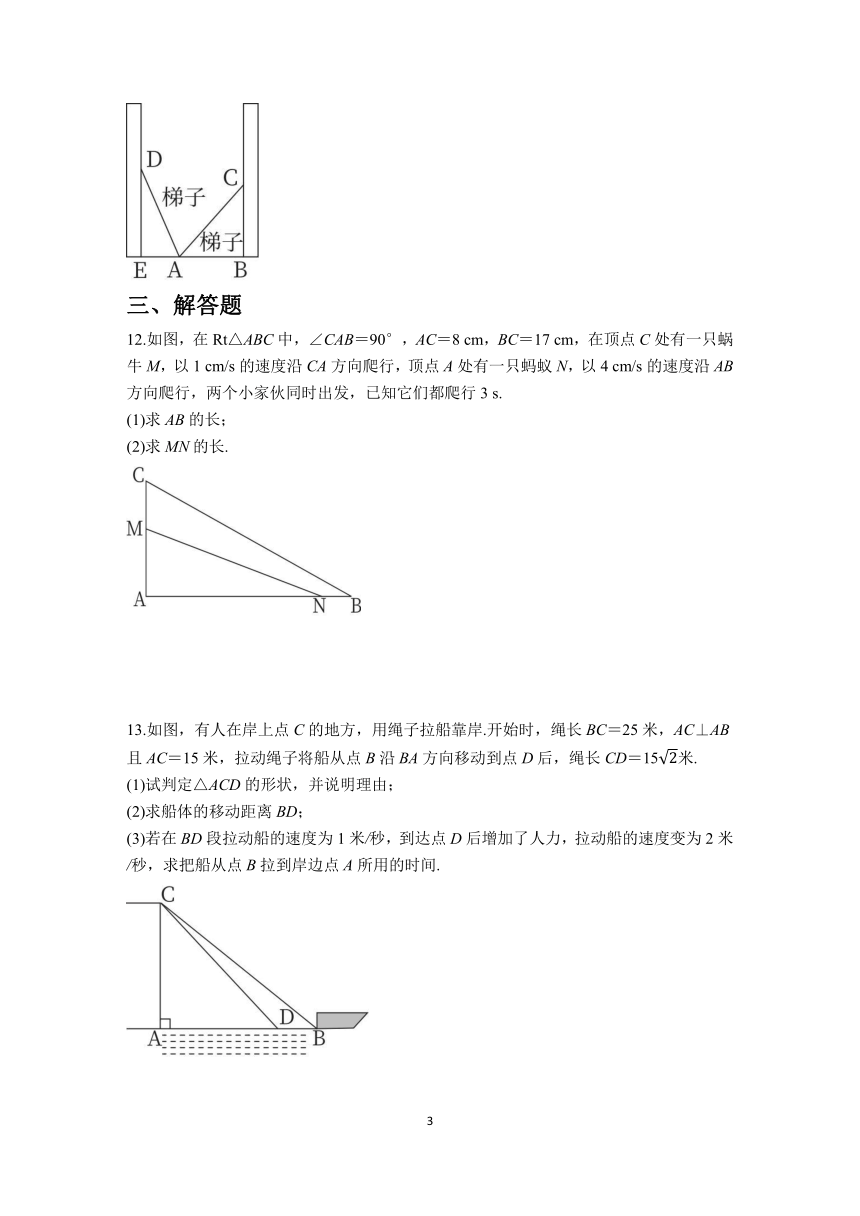
11.某小区两面直立的墙壁之间为安全通道,一架梯子斜靠在左墙DE时,梯子底端A到左墙的距离AE为0.7 m,梯子顶端D到地面的距离DE为2.4 m.若梯子底端A保持不动,将梯子斜靠在右墙BC上,梯子顶端C到地面的距离CB为2 m,则这两面直立墙壁之间的安全通道的宽BE为 m.
三、解答题
12.如图,在Rt△ABC中,∠CAB=90°,AC=8 cm,BC=17 cm,在顶点C处有一只蜗牛M,以1 cm/s的速度沿CA方向爬行,顶点A处有一只蚂蚁N,以4 cm/s的速度沿AB方向爬行,两个小家伙同时出发,已知它们都爬行3 s.
(1)求AB的长;
(2)求MN的长.
13.如图,有人在岸上点C的地方,用绳子拉船靠岸.开始时,绳长BC=25米,AC⊥AB且AC=15米,拉动绳子将船从点B沿BA方向移动到点D后,绳长CD=15米.
(1)试判定△ACD的形状,并说明理由;
(2)求船体的移动距离BD;
(3)若在BD段拉动船的速度为1米/秒,到达点D后增加了人力,拉动船的速度变为2米/秒,求把船从点B拉到岸边点A所用的时间.
14.有一块直角三角形的绿地,量得两条直角边长分别为6 m,8 m,现在要将绿地扩充成等腰三角形,且扩充部分是以8 m为一条直角边的直角三角形,求扩充后等腰三角形绿地的周长.
1
参考答案
一、选择题
1.一只蚂蚁在水平地面上朝正东方向爬行12 cm,再朝正南方向爬行16 cm,这时它离出发点的距离为( C )
A.15 cm B.18 cm C.20 cm D.28 cm
2.如图,湖的两岸有A,B两点,在与AB垂直的BC方向上的点C处测得AC=50米,BC=30米,则A,B两点间的距离为( A )
A.40米 B.30米
C.50米 D.10米
3.在同一水平面上有两棵树,一棵树高10 m,另一棵树高4 m,两树相距8 m.一只小鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少要飞行( B )
A.8 m B.10 m C.12 m D.14 m
4.如图,为了测算出学校旗杆的高度,小明将升旗的绳子拉到旗杆底端,并在与旗杆等长的地方打了一个结,然后将绳子底端拉到离旗杆底端5米的地面某处,发现此时绳子底端距离打结处1米,则旗杆的高度是( A )
A.12米 B.13米 C.15米 D.24米
5.如图是一扇高为2 m、宽为1.5 m的门框.李师傅有3块薄木板,尺寸如下:①号木板长3 m,宽2.7 m;②号木板长2.8 m,宽2.8 m;③号木板长4 m,宽2.4 m.可以从这扇门通过的木板是( C )
A.①号 B.②号C.③号 D.均不能通过
二、填空题
6.如果梯子的底端离建筑物9米,那么15米长的梯子可以到达的建筑物的高度是 米.
【答案】12
7.如图是某路口草坪的一角(∠ACB=90°),当行走路线是A→C→B时,有人为了抄近道在草坪内走出了一条不该有的“捷径”AB.某学习实践小组测量得AC的长约为12米,BC的长约为5米,为了提醒居民爱护草坪,他们想在A,B处设立“踏破芳草可惜,多行数步无妨”的提示牌,则提示牌上的“多行数步”是指约多行 步.(取1步=0.5米)
【答案】8
8.如图,某斜拉桥的主梁AD垂直于桥面MN于点D,主梁上两根拉索AB,AC的长分别为13米、20米,主梁AD的高度为12米,则固定点B,C之间的距离为 米.
【答案】21
9.一艘船由A港沿北偏东60°方向航行30 km至B港,然后再沿北偏西30°方向航行40 km至C港,则A,C两港之间的距离为 km.
【答案】50
10.如图,某会展中心在会展期间准备在高5米、长13米、宽2米的楼道上铺地毯.已知地毯的价格为18元/米2,请你帮助计算一下,铺完这个楼道至少需要 元钱.
【答案】612
11.某小区两面直立的墙壁之间为安全通道,一架梯子斜靠在左墙DE时,梯子底端A到左墙的距离AE为0.7 m,梯子顶端D到地面的距离DE为2.4 m.若梯子底端A保持不动,将梯子斜靠在右墙BC上,梯子顶端C到地面的距离CB为2 m,则这两面直立墙壁之间的安全通道的宽BE为 m.
【答案】2.2
三、解答题
12.如图,在Rt△ABC中,∠CAB=90°,AC=8 cm,BC=17 cm,在顶点C处有一只蜗牛M,以1 cm/s的速度沿CA方向爬行,顶点A处有一只蚂蚁N,以4 cm/s的速度沿AB方向爬行,两个小家伙同时出发,已知它们都爬行3 s.
(1)求AB的长;
(2)求MN的长.
解:(1)AB==15 cm.
(2)由题意知CM=3,AN=12,
则AM=AC-CM=5,
在Rt△MAN中,∠MAN=90°,
∴MN==13 cm.
13.如图,有人在岸上点C的地方,用绳子拉船靠岸.开始时,绳长BC=25米,AC⊥AB且AC=15米,拉动绳子将船从点B沿BA方向移动到点D后,绳长CD=15米.
(1)试判定△ACD的形状,并说明理由;
(2)求船体的移动距离BD;
(3)若在BD段拉动船的速度为1米/秒,到达点D后增加了人力,拉动船的速度变为2米/秒,求把船从点B拉到岸边点A所用的时间.
解:(1)△ACD是等腰直角三角形.理由如下:
在Rt△ACD中,∠A=90°,AC=15,CD=15,
∴AD==15,
∴AC=AD,即△ACD是等腰直角三角形.
(2)在Rt△ABC中,∠A=90°,BC=25,AC=15,
∴AB==20,
∴BD=AB-AD=20-15=5(米).
答:船体的移动距离BD为5米.
(3)5÷1+15÷2=12.5(秒).
答:把船从点B拉到岸边点A所用的时间为12.5秒.
14.有一块直角三角形的绿地,量得两条直角边长分别为6 m,8 m,现在要将绿地扩充成等腰三角形,且扩充部分是以8 m为一条直角边的直角三角形,求扩充后等腰三角形绿地的周长.
解:在Rt△ABC中,∠ACB=90°,AC=8,BC=6,由勾股定理得AB=10,分以下四种情况:
①如图1,当AB=AD=10时,
∵AC⊥BD,∴CD=CB=6,
∴△ABD的周长=10+10+2×6=32(m);
②如图2,当AB=BD=10时,∵BC=6,
∴CD=10-6=4,∴AD==4,
∴△ABD的周长=10+10+4=(20+4) m;
③如图3,当AB为底时,设AD=BD=x,则CD=x-6,由勾股定理得x2=82+(x-6)2,解得x=,
∴△ABD的周长=10+×2=(m);
④如图4,延长AC,使CD=AC=8 m,
∴扩充部分是以8 m为一条直角边的直角三角形,
∴△ABD的周长=(10+8)×2=36(m).
综上所述,扩充后等腰三角形绿地的周长为32 m或(20+4) m或 m或36 m.
图1 图2 图3 图4
17.1 勾股定理
第2课时 勾股定理的实际应用
一、选择题
1.一只蚂蚁在水平地面上朝正东方向爬行12 cm,再朝正南方向爬行16 cm,这时它离出发点的距离为( )
A.15 cm B.18 cm C.20 cm D.28 cm
2.如图,湖的两岸有A,B两点,在与AB垂直的BC方向上的点C处测得AC=50米,BC=30米,则A,B两点间的距离为( )
A.40米 B.30米
C.50米 D.10米
3.在同一水平面上有两棵树,一棵树高10 m,另一棵树高4 m,两树相距8 m.一只小鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少要飞行( )
A.8 m B.10 m C.12 m D.14 m
4.如图,为了测算出学校旗杆的高度,小明将升旗的绳子拉到旗杆底端,并在与旗杆等长的地方打了一个结,然后将绳子底端拉到离旗杆底端5米的地面某处,发现此时绳子底端距离打结处1米,则旗杆的高度是( )
A.12米 B.13米 C.15米 D.24米
5.如图是一扇高为2 m、宽为1.5 m的门框.李师傅有3块薄木板,尺寸如下:①号木板长3 m,宽2.7 m;②号木板长2.8 m,宽2.8 m;③号木板长4 m,宽2.4 m.可以从这扇门通过的木板是( )
A.①号 B.②号C.③号 D.均不能通过
二、填空题
6.如果梯子的底端离建筑物9米,那么15米长的梯子可以到达的建筑物的高度是 米.
7.如图是某路口草坪的一角(∠ACB=90°),当行走路线是A→C→B时,有人为了抄近道在草坪内走出了一条不该有的“捷径”AB.某学习实践小组测量得AC的长约为12米,BC的长约为5米,为了提醒居民爱护草坪,他们想在A,B处设立“踏破芳草可惜,多行数步无妨”的提示牌,则提示牌上的“多行数步”是指约多行 步.(取1步=0.5米)
8.如图,某斜拉桥的主梁AD垂直于桥面MN于点D,主梁上两根拉索AB,AC的长分别为13米、20米,主梁AD的高度为12米,则固定点B,C之间的距离为 米.
9.一艘船由A港沿北偏东60°方向航行30 km至B港,然后再沿北偏西30°方向航行40 km至C港,则A,C两港之间的距离为 km.
10.如图,某会展中心在会展期间准备在高5米、长13米、宽2米的楼道上铺地毯.已知地毯的价格为18元/米2,请你帮助计算一下,铺完这个楼道至少需要 元钱.
11.某小区两面直立的墙壁之间为安全通道,一架梯子斜靠在左墙DE时,梯子底端A到左墙的距离AE为0.7 m,梯子顶端D到地面的距离DE为2.4 m.若梯子底端A保持不动,将梯子斜靠在右墙BC上,梯子顶端C到地面的距离CB为2 m,则这两面直立墙壁之间的安全通道的宽BE为 m.
三、解答题
12.如图,在Rt△ABC中,∠CAB=90°,AC=8 cm,BC=17 cm,在顶点C处有一只蜗牛M,以1 cm/s的速度沿CA方向爬行,顶点A处有一只蚂蚁N,以4 cm/s的速度沿AB方向爬行,两个小家伙同时出发,已知它们都爬行3 s.
(1)求AB的长;
(2)求MN的长.
13.如图,有人在岸上点C的地方,用绳子拉船靠岸.开始时,绳长BC=25米,AC⊥AB且AC=15米,拉动绳子将船从点B沿BA方向移动到点D后,绳长CD=15米.
(1)试判定△ACD的形状,并说明理由;
(2)求船体的移动距离BD;
(3)若在BD段拉动船的速度为1米/秒,到达点D后增加了人力,拉动船的速度变为2米/秒,求把船从点B拉到岸边点A所用的时间.
14.有一块直角三角形的绿地,量得两条直角边长分别为6 m,8 m,现在要将绿地扩充成等腰三角形,且扩充部分是以8 m为一条直角边的直角三角形,求扩充后等腰三角形绿地的周长.
1
参考答案
一、选择题
1.一只蚂蚁在水平地面上朝正东方向爬行12 cm,再朝正南方向爬行16 cm,这时它离出发点的距离为( C )
A.15 cm B.18 cm C.20 cm D.28 cm
2.如图,湖的两岸有A,B两点,在与AB垂直的BC方向上的点C处测得AC=50米,BC=30米,则A,B两点间的距离为( A )
A.40米 B.30米
C.50米 D.10米
3.在同一水平面上有两棵树,一棵树高10 m,另一棵树高4 m,两树相距8 m.一只小鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少要飞行( B )
A.8 m B.10 m C.12 m D.14 m
4.如图,为了测算出学校旗杆的高度,小明将升旗的绳子拉到旗杆底端,并在与旗杆等长的地方打了一个结,然后将绳子底端拉到离旗杆底端5米的地面某处,发现此时绳子底端距离打结处1米,则旗杆的高度是( A )
A.12米 B.13米 C.15米 D.24米
5.如图是一扇高为2 m、宽为1.5 m的门框.李师傅有3块薄木板,尺寸如下:①号木板长3 m,宽2.7 m;②号木板长2.8 m,宽2.8 m;③号木板长4 m,宽2.4 m.可以从这扇门通过的木板是( C )
A.①号 B.②号C.③号 D.均不能通过
二、填空题
6.如果梯子的底端离建筑物9米,那么15米长的梯子可以到达的建筑物的高度是 米.
【答案】12
7.如图是某路口草坪的一角(∠ACB=90°),当行走路线是A→C→B时,有人为了抄近道在草坪内走出了一条不该有的“捷径”AB.某学习实践小组测量得AC的长约为12米,BC的长约为5米,为了提醒居民爱护草坪,他们想在A,B处设立“踏破芳草可惜,多行数步无妨”的提示牌,则提示牌上的“多行数步”是指约多行 步.(取1步=0.5米)
【答案】8
8.如图,某斜拉桥的主梁AD垂直于桥面MN于点D,主梁上两根拉索AB,AC的长分别为13米、20米,主梁AD的高度为12米,则固定点B,C之间的距离为 米.
【答案】21
9.一艘船由A港沿北偏东60°方向航行30 km至B港,然后再沿北偏西30°方向航行40 km至C港,则A,C两港之间的距离为 km.
【答案】50
10.如图,某会展中心在会展期间准备在高5米、长13米、宽2米的楼道上铺地毯.已知地毯的价格为18元/米2,请你帮助计算一下,铺完这个楼道至少需要 元钱.
【答案】612
11.某小区两面直立的墙壁之间为安全通道,一架梯子斜靠在左墙DE时,梯子底端A到左墙的距离AE为0.7 m,梯子顶端D到地面的距离DE为2.4 m.若梯子底端A保持不动,将梯子斜靠在右墙BC上,梯子顶端C到地面的距离CB为2 m,则这两面直立墙壁之间的安全通道的宽BE为 m.
【答案】2.2
三、解答题
12.如图,在Rt△ABC中,∠CAB=90°,AC=8 cm,BC=17 cm,在顶点C处有一只蜗牛M,以1 cm/s的速度沿CA方向爬行,顶点A处有一只蚂蚁N,以4 cm/s的速度沿AB方向爬行,两个小家伙同时出发,已知它们都爬行3 s.
(1)求AB的长;
(2)求MN的长.
解:(1)AB==15 cm.
(2)由题意知CM=3,AN=12,
则AM=AC-CM=5,
在Rt△MAN中,∠MAN=90°,
∴MN==13 cm.
13.如图,有人在岸上点C的地方,用绳子拉船靠岸.开始时,绳长BC=25米,AC⊥AB且AC=15米,拉动绳子将船从点B沿BA方向移动到点D后,绳长CD=15米.
(1)试判定△ACD的形状,并说明理由;
(2)求船体的移动距离BD;
(3)若在BD段拉动船的速度为1米/秒,到达点D后增加了人力,拉动船的速度变为2米/秒,求把船从点B拉到岸边点A所用的时间.
解:(1)△ACD是等腰直角三角形.理由如下:
在Rt△ACD中,∠A=90°,AC=15,CD=15,
∴AD==15,
∴AC=AD,即△ACD是等腰直角三角形.
(2)在Rt△ABC中,∠A=90°,BC=25,AC=15,
∴AB==20,
∴BD=AB-AD=20-15=5(米).
答:船体的移动距离BD为5米.
(3)5÷1+15÷2=12.5(秒).
答:把船从点B拉到岸边点A所用的时间为12.5秒.
14.有一块直角三角形的绿地,量得两条直角边长分别为6 m,8 m,现在要将绿地扩充成等腰三角形,且扩充部分是以8 m为一条直角边的直角三角形,求扩充后等腰三角形绿地的周长.
解:在Rt△ABC中,∠ACB=90°,AC=8,BC=6,由勾股定理得AB=10,分以下四种情况:
①如图1,当AB=AD=10时,
∵AC⊥BD,∴CD=CB=6,
∴△ABD的周长=10+10+2×6=32(m);
②如图2,当AB=BD=10时,∵BC=6,
∴CD=10-6=4,∴AD==4,
∴△ABD的周长=10+10+4=(20+4) m;
③如图3,当AB为底时,设AD=BD=x,则CD=x-6,由勾股定理得x2=82+(x-6)2,解得x=,
∴△ABD的周长=10+×2=(m);
④如图4,延长AC,使CD=AC=8 m,
∴扩充部分是以8 m为一条直角边的直角三角形,
∴△ABD的周长=(10+8)×2=36(m).
综上所述,扩充后等腰三角形绿地的周长为32 m或(20+4) m或 m或36 m.
图1 图2 图3 图4
