人教版八年级下册17.1.1 勾股定理的认识 同步练习(含答案)
文档属性
| 名称 | 人教版八年级下册17.1.1 勾股定理的认识 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 220.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-09 19:23:06 | ||
图片预览

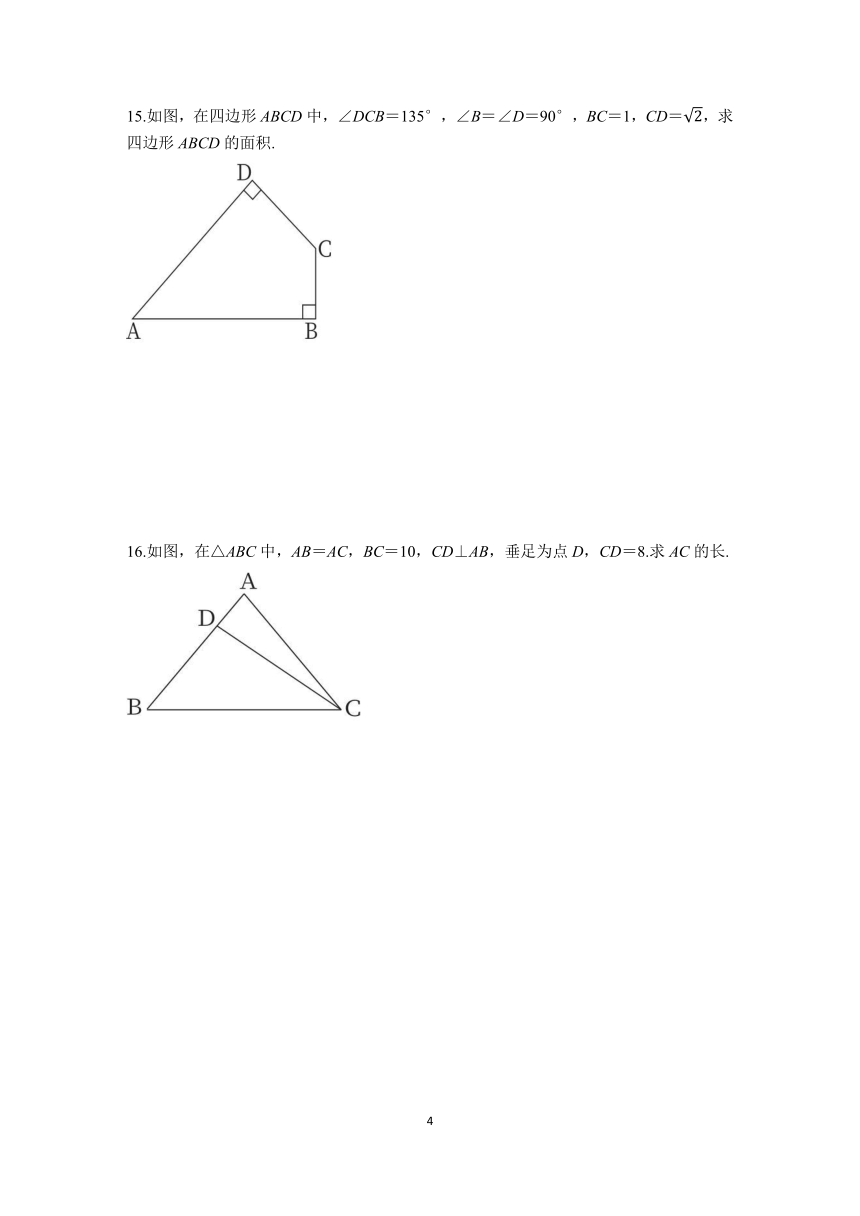
文档简介
第十七章 勾股定理
17.1 勾股定理
第1课时 勾股定理的认识
一、选择题
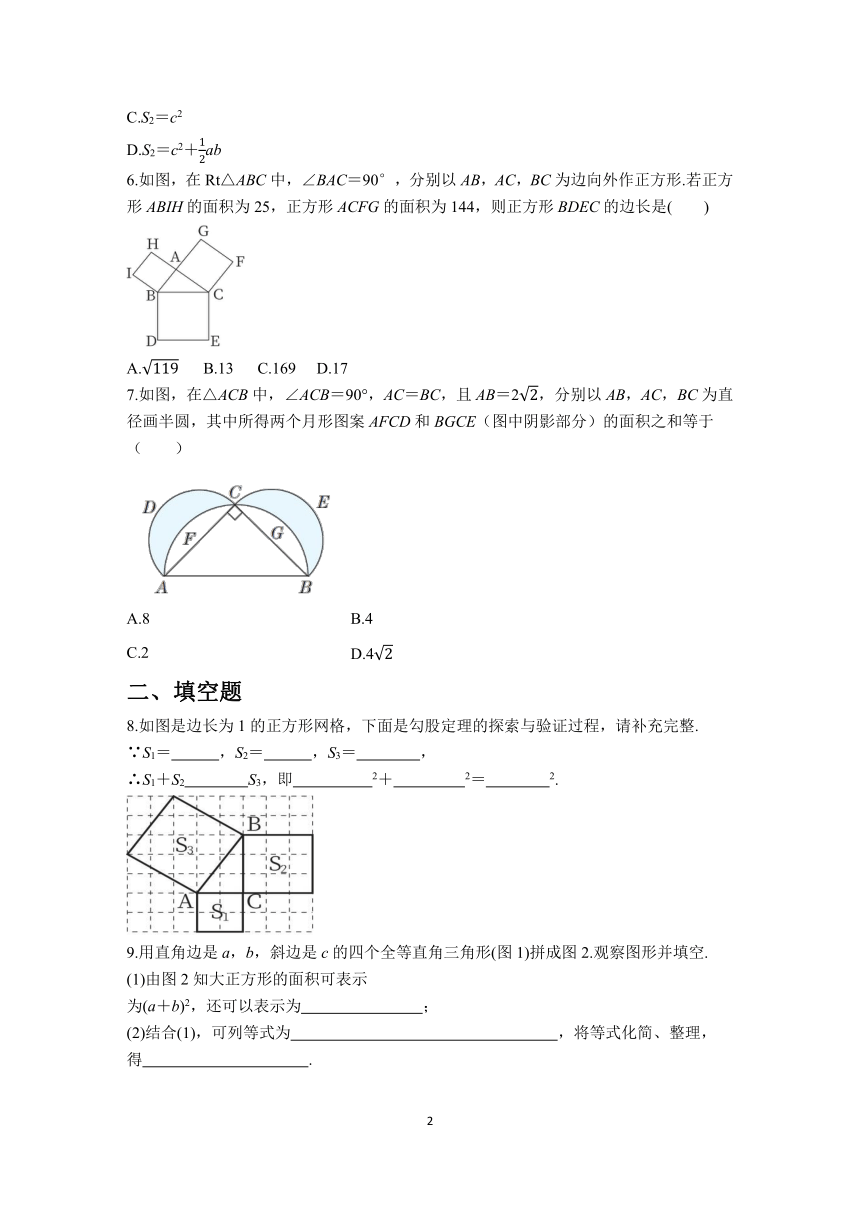
1.下面四幅图中,不能证明勾股定理的是( )
2.勾股定理在《九章算术》中的表述是:“勾股术曰:勾股各自乘,并而开方除之,即弦”,即c=(a为勾,b为股,c为弦).若“勾”为1,“股”为3,则与“弦”最接近的整数是( )
A.2 B.3 C.4 D.5
3.若Rt△ABC的三边长分别为a,b,c,且c2=10,b2=6,则a的值是( )
A.2 B.2或4 C.4 D.4或16
4.如图,在四边形ABCD中,∠DAB=∠BCD=90°,分别以四边形ABCD的四条边为边向外作四个正方形,面积分别为S1,S2,S3,S4.若S1=48,S2+S3=135,则S4=( )
A.183 B.87
C.119 D.81
5.意大利著名画家达·芬奇用如图所示的方法证明了勾股定理.若设如图中空白部分的面积为S1,右图中空白部分的面积为S2,则下列表示S1,S2的等式成立的是( )
A.S1=a2+b2+2ab
B.S1=a2+b2+ab
C.S2=c2
D.S2=c2+ab
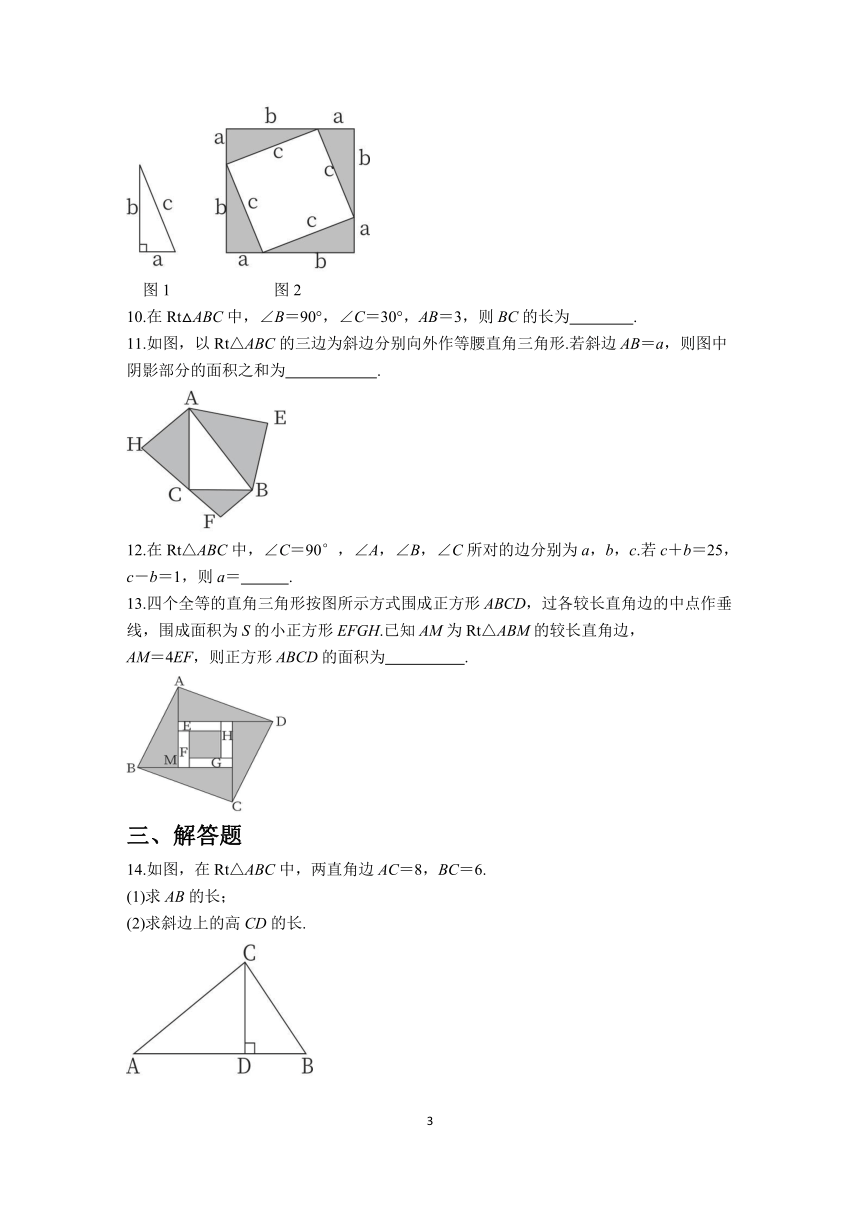
6.如图,在Rt△ABC中,∠BAC=90°,分别以AB,AC,BC为边向外作正方形.若正方形ABIH的面积为25,正方形ACFG的面积为144,则正方形BDEC的边长是( )
A. B.13 C.169 D.17
7.如图,在△ACB中,∠ACB=90°,AC=BC,且AB=2,分别以AB,AC,BC为直径画半圆,其中所得两个月形图案AFCD和BGCE(图中阴影部分)的面积之和等于( )
A.8 B.4
C.2 D.4
二、填空题
8.如图是边长为1的正方形网格,下面是勾股定理的探索与验证过程,请补充完整.
∵S1= ,S2= ,S3= ,
∴S1+S2 S3,即 2+ 2= 2.
9.用直角边是a,b,斜边是c的四个全等直角三角形(图1)拼成图2.观察图形并填空.
(1)由图2知大正方形的面积可表示
为(a+b)2,还可以表示为 ;
(2)结合(1),可列等式为 ,将等式化简、整理,得 .
图1 图2
10.在Rt△ABC中,∠B=90°,∠C=30°,AB=3,则BC的长为 .
11.如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=a,则图中阴影部分的面积之和为 .
12.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c.若c+b=25,c-b=1,则a= .
13.四个全等的直角三角形按图所示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为S的小正方形EFGH.已知AM为Rt△ABM的较长直角边,
AM=4EF,则正方形ABCD的面积为 .
三、解答题
14.如图,在Rt△ABC中,两直角边AC=8,BC=6.
(1)求AB的长;
(2)求斜边上的高CD的长.
15.如图,在四边形ABCD中,∠DCB=135°,∠B=∠D=90°,BC=1,CD=,求四边形ABCD的面积.
16.如图,在△ABC中,AB=AC,BC=10,CD⊥AB,垂足为点D,CD=8.求AC的长.
1
参考答案
一、选择题
1.下面四幅图中,不能证明勾股定理的是( D )
2.勾股定理在《九章算术》中的表述是:“勾股术曰:勾股各自乘,并而开方除之,即弦”,即c=(a为勾,b为股,c为弦).若“勾”为1,“股”为3,则与“弦”最接近的整数是( B )
A.2 B.3 C.4 D.5
3.若Rt△ABC的三边长分别为a,b,c,且c2=10,b2=6,则a的值是( B )
A.2 B.2或4 C.4 D.4或16
4.如图,在四边形ABCD中,∠DAB=∠BCD=90°,分别以四边形ABCD的四条边为边向外作四个正方形,面积分别为S1,S2,S3,S4.若S1=48,S2+S3=135,则S4=( B )
A.183 B.87
C.119 D.81
5.意大利著名画家达·芬奇用如图所示的方法证明了勾股定理.若设如图中空白部分的面积为S1,右图中空白部分的面积为S2,则下列表示S1,S2的等式成立的是( B )
A.S1=a2+b2+2ab
B.S1=a2+b2+ab
C.S2=c2
D.S2=c2+ab
6.如图,在Rt△ABC中,∠BAC=90°,分别以AB,AC,BC为边向外作正方形.若正方形ABIH的面积为25,正方形ACFG的面积为144,则正方形BDEC的边长是( B )
A. B.13 C.169 D.17
7.如图,在△ACB中,∠ACB=90°,AC=BC,且AB=2,分别以AB,AC,BC为直径画半圆,其中所得两个月形图案AFCD和BGCE(图中阴影部分)的面积之和等于( C )
A.8 B.4
C.2 D.4
二、填空题
8.如图是边长为1的正方形网格,下面是勾股定理的探索与验证过程,请补充完整.
∵S1= ,S2= ,S3= ,
∴S1+S2 S3,即 2+ 2= 2.
【答案】4 9 13 = AC BC AB
9.用直角边是a,b,斜边是c的四个全等直角三角形(图1)拼成图2.观察图形并填空.
(1)由图2知大正方形的面积可表示
为(a+b)2,还可以表示为 ;
(2)结合(1),可列等式为 ,将等式化简、整理,得 .
图1 图2
【答案】 c2+2ab (a+b)2=c2+2ab a2+b2=c2
10.在Rt△ABC中,∠B=90°,∠C=30°,AB=3,则BC的长为 .
【答案】3
11.如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=a,则图中阴影部分的面积之和为 .
【答案】2
12.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c.若c+b=25,c-b=1,则a= .
【答案】5
13.四个全等的直角三角形按图所示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为S的小正方形EFGH.已知AM为Rt△ABM的较长直角边,
AM=4EF,则正方形ABCD的面积为 .
【答案】17S
【解析】设AM=a,BM=b,则正方形ABCD的面积=a2+b2,由题意可知EF=-(-b)=b,因为AM=4EF,所以a=4b,因为正方形EFGH的面积为S,所以S=b2,所以正方形ABCD的面积=a2+b2=17b2=17S.
三、解答题
14.如图,在Rt△ABC中,两直角边AC=8,BC=6.
(1)求AB的长;
(2)求斜边上的高CD的长.
解:(1)由勾股定理,得AB==10.
(2)由题意,得S△ABC=·CD=·BC,
∴CD=.
15.如图,在四边形ABCD中,∠DCB=135°,∠B=∠D=90°,BC=1,CD=,求四边形ABCD的面积.
解:延长AD,交BC的延长线于点E.
∵∠DCB=135°,∠ADC=90°,
∴∠DCE=45°,∠EDC=90°,
∴∠E=∠DCE=45°,∴DE=CD=,
∴在Rt△CDE中,CE==2,
∴BE=BC+CE=3.
∵∠B=90°,∠E=45°,
∴∠A=∠E=45°,∴AB=BE=3,
∴S四边形ABCD=S△EAB-S△CDE=.
16.如图,在△ABC中,AB=AC,BC=10,CD⊥AB,垂足为点D,CD=8.求AC的长.
解:∵CD⊥AB,∴∠ADC=∠BDC=90°.
在Rt△BCD中,BD==6.
设AC=AB=x,则AD=x-6.
在Rt△ACD中,AC2=AD2+CD2,
即x2=(x-6)2+82,
解得x=,即AC的长为.
17.1 勾股定理
第1课时 勾股定理的认识
一、选择题
1.下面四幅图中,不能证明勾股定理的是( )
2.勾股定理在《九章算术》中的表述是:“勾股术曰:勾股各自乘,并而开方除之,即弦”,即c=(a为勾,b为股,c为弦).若“勾”为1,“股”为3,则与“弦”最接近的整数是( )
A.2 B.3 C.4 D.5
3.若Rt△ABC的三边长分别为a,b,c,且c2=10,b2=6,则a的值是( )
A.2 B.2或4 C.4 D.4或16
4.如图,在四边形ABCD中,∠DAB=∠BCD=90°,分别以四边形ABCD的四条边为边向外作四个正方形,面积分别为S1,S2,S3,S4.若S1=48,S2+S3=135,则S4=( )
A.183 B.87
C.119 D.81
5.意大利著名画家达·芬奇用如图所示的方法证明了勾股定理.若设如图中空白部分的面积为S1,右图中空白部分的面积为S2,则下列表示S1,S2的等式成立的是( )
A.S1=a2+b2+2ab
B.S1=a2+b2+ab
C.S2=c2
D.S2=c2+ab
6.如图,在Rt△ABC中,∠BAC=90°,分别以AB,AC,BC为边向外作正方形.若正方形ABIH的面积为25,正方形ACFG的面积为144,则正方形BDEC的边长是( )
A. B.13 C.169 D.17
7.如图,在△ACB中,∠ACB=90°,AC=BC,且AB=2,分别以AB,AC,BC为直径画半圆,其中所得两个月形图案AFCD和BGCE(图中阴影部分)的面积之和等于( )
A.8 B.4
C.2 D.4
二、填空题
8.如图是边长为1的正方形网格,下面是勾股定理的探索与验证过程,请补充完整.
∵S1= ,S2= ,S3= ,
∴S1+S2 S3,即 2+ 2= 2.
9.用直角边是a,b,斜边是c的四个全等直角三角形(图1)拼成图2.观察图形并填空.
(1)由图2知大正方形的面积可表示
为(a+b)2,还可以表示为 ;
(2)结合(1),可列等式为 ,将等式化简、整理,得 .
图1 图2
10.在Rt△ABC中,∠B=90°,∠C=30°,AB=3,则BC的长为 .
11.如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=a,则图中阴影部分的面积之和为 .
12.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c.若c+b=25,c-b=1,则a= .
13.四个全等的直角三角形按图所示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为S的小正方形EFGH.已知AM为Rt△ABM的较长直角边,
AM=4EF,则正方形ABCD的面积为 .
三、解答题
14.如图,在Rt△ABC中,两直角边AC=8,BC=6.
(1)求AB的长;
(2)求斜边上的高CD的长.
15.如图,在四边形ABCD中,∠DCB=135°,∠B=∠D=90°,BC=1,CD=,求四边形ABCD的面积.
16.如图,在△ABC中,AB=AC,BC=10,CD⊥AB,垂足为点D,CD=8.求AC的长.
1
参考答案
一、选择题
1.下面四幅图中,不能证明勾股定理的是( D )
2.勾股定理在《九章算术》中的表述是:“勾股术曰:勾股各自乘,并而开方除之,即弦”,即c=(a为勾,b为股,c为弦).若“勾”为1,“股”为3,则与“弦”最接近的整数是( B )
A.2 B.3 C.4 D.5
3.若Rt△ABC的三边长分别为a,b,c,且c2=10,b2=6,则a的值是( B )
A.2 B.2或4 C.4 D.4或16
4.如图,在四边形ABCD中,∠DAB=∠BCD=90°,分别以四边形ABCD的四条边为边向外作四个正方形,面积分别为S1,S2,S3,S4.若S1=48,S2+S3=135,则S4=( B )
A.183 B.87
C.119 D.81
5.意大利著名画家达·芬奇用如图所示的方法证明了勾股定理.若设如图中空白部分的面积为S1,右图中空白部分的面积为S2,则下列表示S1,S2的等式成立的是( B )
A.S1=a2+b2+2ab
B.S1=a2+b2+ab
C.S2=c2
D.S2=c2+ab
6.如图,在Rt△ABC中,∠BAC=90°,分别以AB,AC,BC为边向外作正方形.若正方形ABIH的面积为25,正方形ACFG的面积为144,则正方形BDEC的边长是( B )
A. B.13 C.169 D.17
7.如图,在△ACB中,∠ACB=90°,AC=BC,且AB=2,分别以AB,AC,BC为直径画半圆,其中所得两个月形图案AFCD和BGCE(图中阴影部分)的面积之和等于( C )
A.8 B.4
C.2 D.4
二、填空题
8.如图是边长为1的正方形网格,下面是勾股定理的探索与验证过程,请补充完整.
∵S1= ,S2= ,S3= ,
∴S1+S2 S3,即 2+ 2= 2.
【答案】4 9 13 = AC BC AB
9.用直角边是a,b,斜边是c的四个全等直角三角形(图1)拼成图2.观察图形并填空.
(1)由图2知大正方形的面积可表示
为(a+b)2,还可以表示为 ;
(2)结合(1),可列等式为 ,将等式化简、整理,得 .
图1 图2
【答案】 c2+2ab (a+b)2=c2+2ab a2+b2=c2
10.在Rt△ABC中,∠B=90°,∠C=30°,AB=3,则BC的长为 .
【答案】3
11.如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=a,则图中阴影部分的面积之和为 .
【答案】2
12.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c.若c+b=25,c-b=1,则a= .
【答案】5
13.四个全等的直角三角形按图所示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为S的小正方形EFGH.已知AM为Rt△ABM的较长直角边,
AM=4EF,则正方形ABCD的面积为 .
【答案】17S
【解析】设AM=a,BM=b,则正方形ABCD的面积=a2+b2,由题意可知EF=-(-b)=b,因为AM=4EF,所以a=4b,因为正方形EFGH的面积为S,所以S=b2,所以正方形ABCD的面积=a2+b2=17b2=17S.
三、解答题
14.如图,在Rt△ABC中,两直角边AC=8,BC=6.
(1)求AB的长;
(2)求斜边上的高CD的长.
解:(1)由勾股定理,得AB==10.
(2)由题意,得S△ABC=·CD=·BC,
∴CD=.
15.如图,在四边形ABCD中,∠DCB=135°,∠B=∠D=90°,BC=1,CD=,求四边形ABCD的面积.
解:延长AD,交BC的延长线于点E.
∵∠DCB=135°,∠ADC=90°,
∴∠DCE=45°,∠EDC=90°,
∴∠E=∠DCE=45°,∴DE=CD=,
∴在Rt△CDE中,CE==2,
∴BE=BC+CE=3.
∵∠B=90°,∠E=45°,
∴∠A=∠E=45°,∴AB=BE=3,
∴S四边形ABCD=S△EAB-S△CDE=.
16.如图,在△ABC中,AB=AC,BC=10,CD⊥AB,垂足为点D,CD=8.求AC的长.
解:∵CD⊥AB,∴∠ADC=∠BDC=90°.
在Rt△BCD中,BD==6.
设AC=AB=x,则AD=x-6.
在Rt△ACD中,AC2=AD2+CD2,
即x2=(x-6)2+82,
解得x=,即AC的长为.
