17.1.3 利用勾股定理作图或计算同步练习(含答案)
文档属性
| 名称 | 17.1.3 利用勾股定理作图或计算同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 228.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-09 00:00:00 | ||
图片预览


文档简介
第十七章 勾股定理
17.1 勾股定理
第3课时 利用勾股定理作图或计算
一、选择题
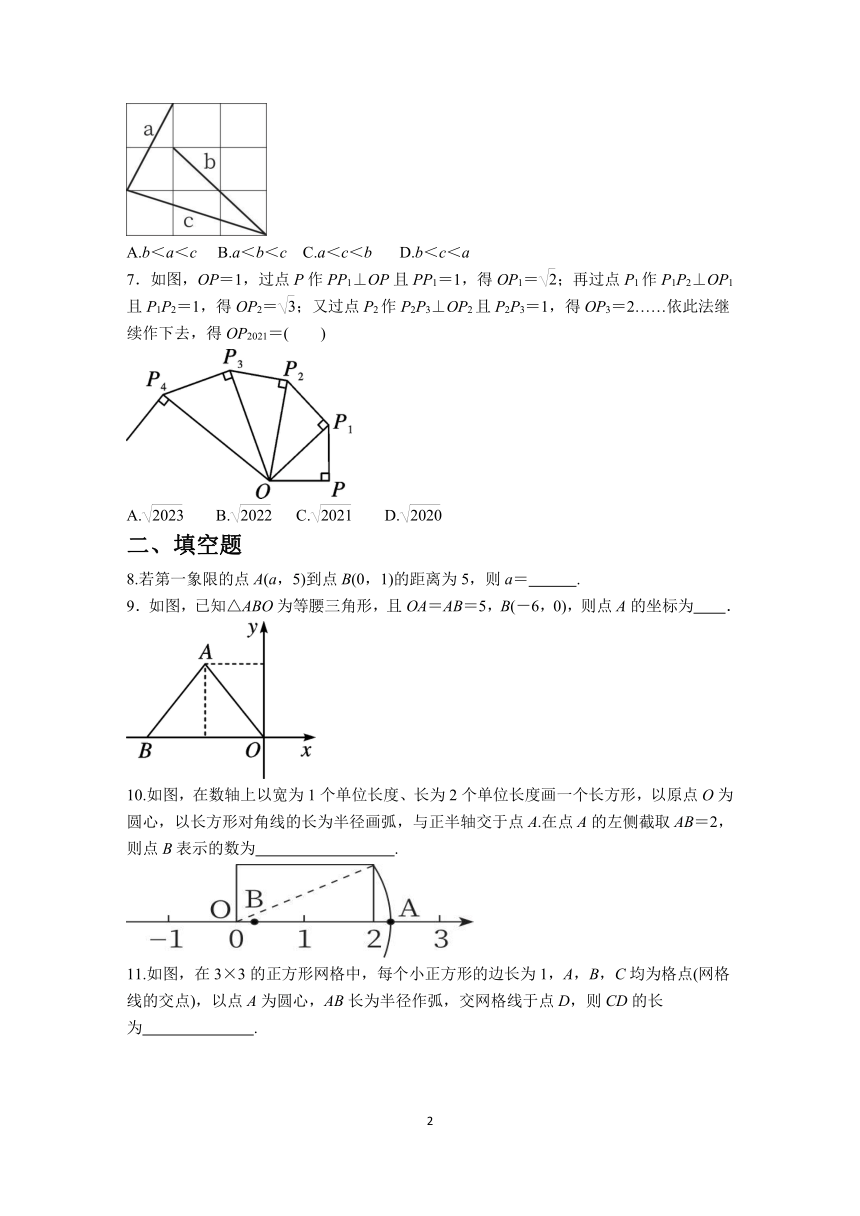
1.在平面直角坐标系中,点A的坐标为(-2,-1),则点A到原点O的距离是( )
A.-5 B.5 C. D.
2.如图,在数轴上找出表示3的点A,过点A作AB⊥OA,AB=2,以点O为圆心,OB长为半径作弧,弧与数轴的交点为C,则点C表示的数是( )
A.- B.- C.-3 D.-
3.如图,数轴上点A表示的数为-2,点B表示的数是1,过点B作BC⊥AB,且BC=2,以点A为圆心,AC长为半径作弧,弧与数轴的交点D表示的数为( )
A. B.+2 C.-2 D.-+2
4.如图,网格中每个小正方形的边长均为1,A,B为网格线的交点,则AB的长为( )
A.3 B.5 C.7 D.12
6.如图,a,b,c是正方形网格中的3条线段,它们的端点都在格点(网格线的交点)上,则关于a,b,c大小关系判断正确的是( )
A.b<a<c B.a<b<c C.a<c<b D.b<c<a
7.如图,OP=1,过点P作PP1⊥OP且PP1=1,得OP1=;再过点P1作P1P2⊥OP1且P1P2=1,得OP2=;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2……依此法继续作下去,得OP2021=( )
A. B. C. D.
二、填空题
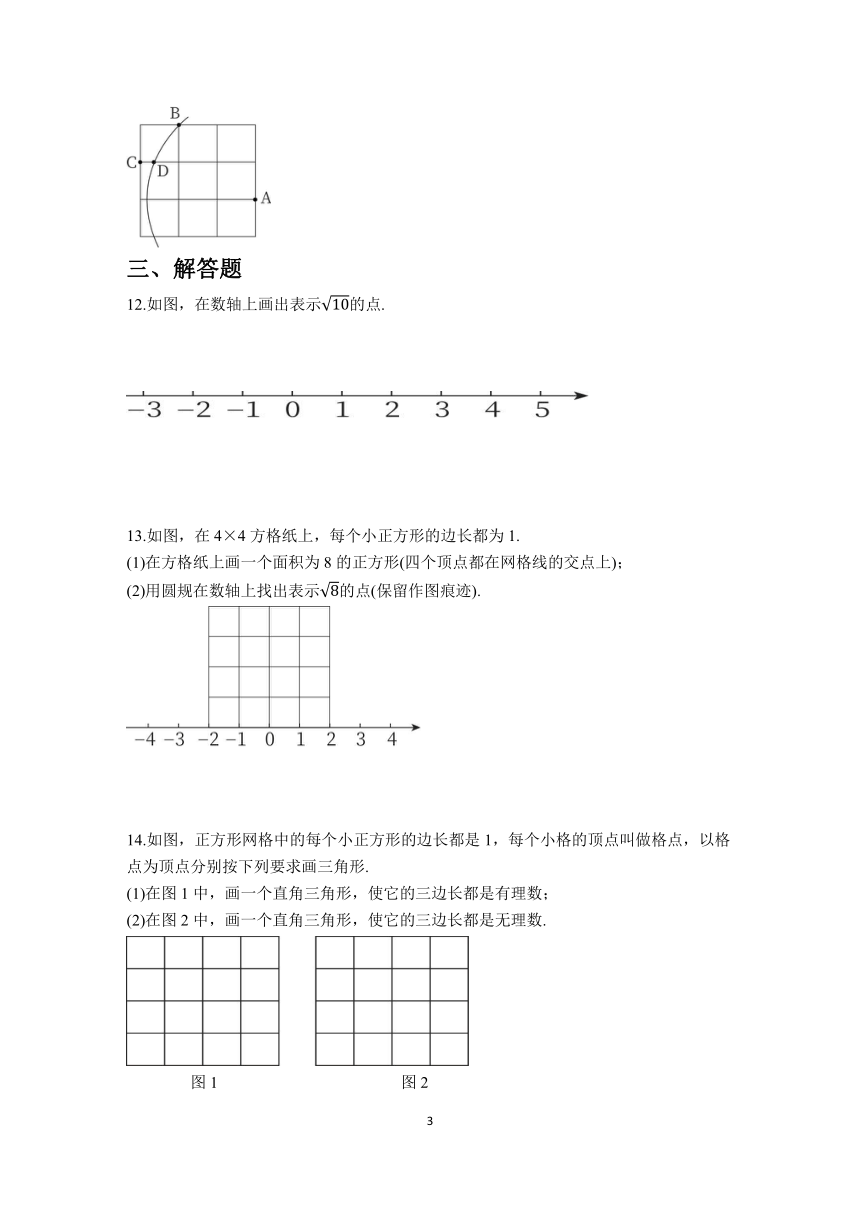
8.若第一象限的点A(a,5)到点B(0,1)的距离为5,则a= .
9.如图,已知△ABO为等腰三角形,且OA=AB=5,B(-6,0),则点A的坐标为 .
10.如图,在数轴上以宽为1个单位长度、长为2个单位长度画一个长方形,以原点O为圆心,以长方形对角线的长为半径画弧,与正半轴交于点A.在点A的左侧截取AB=2,则点B表示的数为 .
11.如图,在3×3的正方形网格中,每个小正方形的边长为1,A,B,C均为格点(网格线的交点),以点A为圆心,AB长为半径作弧,交网格线于点D,则CD的长为 .
三、解答题
12.如图,在数轴上画出表示的点.
13.如图,在4×4方格纸上,每个小正方形的边长都为1.
(1)在方格纸上画一个面积为8的正方形(四个顶点都在网格线的交点上);
(2)用圆规在数轴上找出表示的点(保留作图痕迹).
14.如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(1)在图1中,画一个直角三角形,使它的三边长都是有理数;
(2)在图2中,画一个直角三角形,使它的三边长都是无理数.
图1 图2
15.探究:如图1,把两个边长为1的小正方形沿对角线剪开,所得的4个直角三角形拼成一个面积为2的大正方形.由此,得到了一种能在数轴上画出无理数对应点的方法.
图1 图2
图3 图4
(1)图2中A,B两点表示的数分别为 , .
(2)请你参照上面的方法,对长为5、宽为1的长方形进行裁剪,拼成一个正方形.在图3中画出裁剪线,并在图4位置画出所拼正方形的示意图.
(3)画一条数轴,并在数轴上分别标出表示数以及-3的点.(图中标出必要线段的长度,保留作图痕迹)
1
参考答案
一、选择题
1.在平面直角坐标系中,点A的坐标为(-2,-1),则点A到原点O的距离是( C )
A.-5 B.5 C. D.
2.如图,在数轴上找出表示3的点A,过点A作AB⊥OA,AB=2,以点O为圆心,OB长为半径作弧,弧与数轴的交点为C,则点C表示的数是( A )
A.- B.- C.-3 D.-
3.如图,数轴上点A表示的数为-2,点B表示的数是1,过点B作BC⊥AB,且BC=2,以点A为圆心,AC长为半径作弧,弧与数轴的交点D表示的数为( C )
A. B.+2 C.-2 D.-+2
4.如图,网格中每个小正方形的边长均为1,A,B为网格线的交点,则AB的长为( B )
A.3 B.5 C.7 D.12
6.如图,a,b,c是正方形网格中的3条线段,它们的端点都在格点(网格线的交点)上,则关于a,b,c大小关系判断正确的是( B )
A.b<a<c B.a<b<c C.a<c<b D.b<c<a
7.如图,OP=1,过点P作PP1⊥OP且PP1=1,得OP1=;再过点P1作P1P2⊥OP1且P1P2=1,得OP2=;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2……依此法继续作下去,得OP2021=( B )
A. B. C. D.
二、填空题
8.若第一象限的点A(a,5)到点B(0,1)的距离为5,则a= .
【答案】3
9.如图,已知△ABO为等腰三角形,且OA=AB=5,B(-6,0),则点A的坐标为 .
【答案】(-3,4)
10.如图,在数轴上以宽为1个单位长度、长为2个单位长度画一个长方形,以原点O为圆心,以长方形对角线的长为半径画弧,与正半轴交于点A.在点A的左侧截取AB=2,则点B表示的数为 .
【答案】-2
11.如图,在3×3的正方形网格中,每个小正方形的边长为1,A,B,C均为格点(网格线的交点),以点A为圆心,AB长为半径作弧,交网格线于点D,则CD的长为 .
【答案】3-
三、解答题
12.如图,在数轴上画出表示的点.
略
13.如图,在4×4方格纸上,每个小正方形的边长都为1.
(1)在方格纸上画一个面积为8的正方形(四个顶点都在网格线的交点上);
(2)用圆规在数轴上找出表示的点(保留作图痕迹).
解:(1)如图所示,正方形ABCD即为所求.
(2)如图所示,点E即为所求.
14.如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(1)在图1中,画一个直角三角形,使它的三边长都是有理数;
(2)在图2中,画一个直角三角形,使它的三边长都是无理数.
图1 图2
解:本题答案不唯一,合理即可.
(1)三边分别为3,4,5(如图1).
(2)三边分别为,2(如图2).
图1 图2
15.探究:如图1,把两个边长为1的小正方形沿对角线剪开,所得的4个直角三角形拼成一个面积为2的大正方形.由此,得到了一种能在数轴上画出无理数对应点的方法.
图1 图2
图3 图4
(1)图2中A,B两点表示的数分别为 , .
【答案】1- 1+
(2)请你参照上面的方法,对长为5、宽为1的长方形进行裁剪,拼成一个正方形.在图3中画出裁剪线,并在图4位置画出所拼正方形的示意图.
(3)画一条数轴,并在数轴上分别标出表示数以及
-3的点.(图中标出必要线段的长度,保留作图痕迹)
解:(2)如图所示:
(3)表示数以及-3的点如图所示:
17.1 勾股定理
第3课时 利用勾股定理作图或计算
一、选择题
1.在平面直角坐标系中,点A的坐标为(-2,-1),则点A到原点O的距离是( )
A.-5 B.5 C. D.
2.如图,在数轴上找出表示3的点A,过点A作AB⊥OA,AB=2,以点O为圆心,OB长为半径作弧,弧与数轴的交点为C,则点C表示的数是( )
A.- B.- C.-3 D.-
3.如图,数轴上点A表示的数为-2,点B表示的数是1,过点B作BC⊥AB,且BC=2,以点A为圆心,AC长为半径作弧,弧与数轴的交点D表示的数为( )
A. B.+2 C.-2 D.-+2
4.如图,网格中每个小正方形的边长均为1,A,B为网格线的交点,则AB的长为( )
A.3 B.5 C.7 D.12
6.如图,a,b,c是正方形网格中的3条线段,它们的端点都在格点(网格线的交点)上,则关于a,b,c大小关系判断正确的是( )
A.b<a<c B.a<b<c C.a<c<b D.b<c<a
7.如图,OP=1,过点P作PP1⊥OP且PP1=1,得OP1=;再过点P1作P1P2⊥OP1且P1P2=1,得OP2=;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2……依此法继续作下去,得OP2021=( )
A. B. C. D.
二、填空题
8.若第一象限的点A(a,5)到点B(0,1)的距离为5,则a= .
9.如图,已知△ABO为等腰三角形,且OA=AB=5,B(-6,0),则点A的坐标为 .
10.如图,在数轴上以宽为1个单位长度、长为2个单位长度画一个长方形,以原点O为圆心,以长方形对角线的长为半径画弧,与正半轴交于点A.在点A的左侧截取AB=2,则点B表示的数为 .
11.如图,在3×3的正方形网格中,每个小正方形的边长为1,A,B,C均为格点(网格线的交点),以点A为圆心,AB长为半径作弧,交网格线于点D,则CD的长为 .
三、解答题
12.如图,在数轴上画出表示的点.
13.如图,在4×4方格纸上,每个小正方形的边长都为1.
(1)在方格纸上画一个面积为8的正方形(四个顶点都在网格线的交点上);
(2)用圆规在数轴上找出表示的点(保留作图痕迹).
14.如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(1)在图1中,画一个直角三角形,使它的三边长都是有理数;
(2)在图2中,画一个直角三角形,使它的三边长都是无理数.
图1 图2
15.探究:如图1,把两个边长为1的小正方形沿对角线剪开,所得的4个直角三角形拼成一个面积为2的大正方形.由此,得到了一种能在数轴上画出无理数对应点的方法.
图1 图2
图3 图4
(1)图2中A,B两点表示的数分别为 , .
(2)请你参照上面的方法,对长为5、宽为1的长方形进行裁剪,拼成一个正方形.在图3中画出裁剪线,并在图4位置画出所拼正方形的示意图.
(3)画一条数轴,并在数轴上分别标出表示数以及-3的点.(图中标出必要线段的长度,保留作图痕迹)
1
参考答案
一、选择题
1.在平面直角坐标系中,点A的坐标为(-2,-1),则点A到原点O的距离是( C )
A.-5 B.5 C. D.
2.如图,在数轴上找出表示3的点A,过点A作AB⊥OA,AB=2,以点O为圆心,OB长为半径作弧,弧与数轴的交点为C,则点C表示的数是( A )
A.- B.- C.-3 D.-
3.如图,数轴上点A表示的数为-2,点B表示的数是1,过点B作BC⊥AB,且BC=2,以点A为圆心,AC长为半径作弧,弧与数轴的交点D表示的数为( C )
A. B.+2 C.-2 D.-+2
4.如图,网格中每个小正方形的边长均为1,A,B为网格线的交点,则AB的长为( B )
A.3 B.5 C.7 D.12
6.如图,a,b,c是正方形网格中的3条线段,它们的端点都在格点(网格线的交点)上,则关于a,b,c大小关系判断正确的是( B )
A.b<a<c B.a<b<c C.a<c<b D.b<c<a
7.如图,OP=1,过点P作PP1⊥OP且PP1=1,得OP1=;再过点P1作P1P2⊥OP1且P1P2=1,得OP2=;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2……依此法继续作下去,得OP2021=( B )
A. B. C. D.
二、填空题
8.若第一象限的点A(a,5)到点B(0,1)的距离为5,则a= .
【答案】3
9.如图,已知△ABO为等腰三角形,且OA=AB=5,B(-6,0),则点A的坐标为 .
【答案】(-3,4)
10.如图,在数轴上以宽为1个单位长度、长为2个单位长度画一个长方形,以原点O为圆心,以长方形对角线的长为半径画弧,与正半轴交于点A.在点A的左侧截取AB=2,则点B表示的数为 .
【答案】-2
11.如图,在3×3的正方形网格中,每个小正方形的边长为1,A,B,C均为格点(网格线的交点),以点A为圆心,AB长为半径作弧,交网格线于点D,则CD的长为 .
【答案】3-
三、解答题
12.如图,在数轴上画出表示的点.
略
13.如图,在4×4方格纸上,每个小正方形的边长都为1.
(1)在方格纸上画一个面积为8的正方形(四个顶点都在网格线的交点上);
(2)用圆规在数轴上找出表示的点(保留作图痕迹).
解:(1)如图所示,正方形ABCD即为所求.
(2)如图所示,点E即为所求.
14.如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(1)在图1中,画一个直角三角形,使它的三边长都是有理数;
(2)在图2中,画一个直角三角形,使它的三边长都是无理数.
图1 图2
解:本题答案不唯一,合理即可.
(1)三边分别为3,4,5(如图1).
(2)三边分别为,2(如图2).
图1 图2
15.探究:如图1,把两个边长为1的小正方形沿对角线剪开,所得的4个直角三角形拼成一个面积为2的大正方形.由此,得到了一种能在数轴上画出无理数对应点的方法.
图1 图2
图3 图4
(1)图2中A,B两点表示的数分别为 , .
【答案】1- 1+
(2)请你参照上面的方法,对长为5、宽为1的长方形进行裁剪,拼成一个正方形.在图3中画出裁剪线,并在图4位置画出所拼正方形的示意图.
(3)画一条数轴,并在数轴上分别标出表示数以及
-3的点.(图中标出必要线段的长度,保留作图痕迹)
解:(2)如图所示:
(3)表示数以及-3的点如图所示:
