物理人教版(2019)必修第二册7.4宇宙航行(共29张ppt)
文档属性
| 名称 | 物理人教版(2019)必修第二册7.4宇宙航行(共29张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-03-09 22:21:59 | ||
图片预览







文档简介
(共29张PPT)
7.4 宇宙航行
提示:万有引力提供物体作匀速圆周运动的向心力。这个抛出速度就是做匀速圆周运动的线速度。
探究问题:以多大的速度抛出一个物体,它才会绕地球表面运动,不会落下来?(变成了近地卫星)
(已知G=6.67×10-11N·m2/kg2 , 地球质量M=5.98×1024kg, 地球半径R=6400km)
探究问题一 第一宇宙速度的推导
且 r = R
(地球近地卫星的线速度)
若不知道地球的质量M,只知道地球表面重力加速度g=9.8m/s2,R=6400km,又该如何计算?
地球表面附近,物体受到的重力等于地球对物体的引力,此时重力提供向心力
1.第一宇宙速度既是最小的发射速度,也是最大的环绕速度。
2.不同星体的第一宇宙速度不一样
(1)发射速度:指被发射物在地面附近离开发射装置时的初速度.
(2)运行速度:也叫环绕速度,是指卫星在进入运行轨道后绕地球做匀速圆周运动的线速度。
例1 我国发射了一颗绕月运行的探月卫星“嫦娥一号”。设该卫星的轨道是圆形的,且贴近月球表面,已知月球的质量约为地球质量的,月球的半径约为地球半径的,地球上的第一宇宙速度约为7.9 km/s,则该探月卫星绕月运行的最大速率约为( )
A.0.4 km/s B.1.8 km/s
C.11 km/s D.36 km/s
B
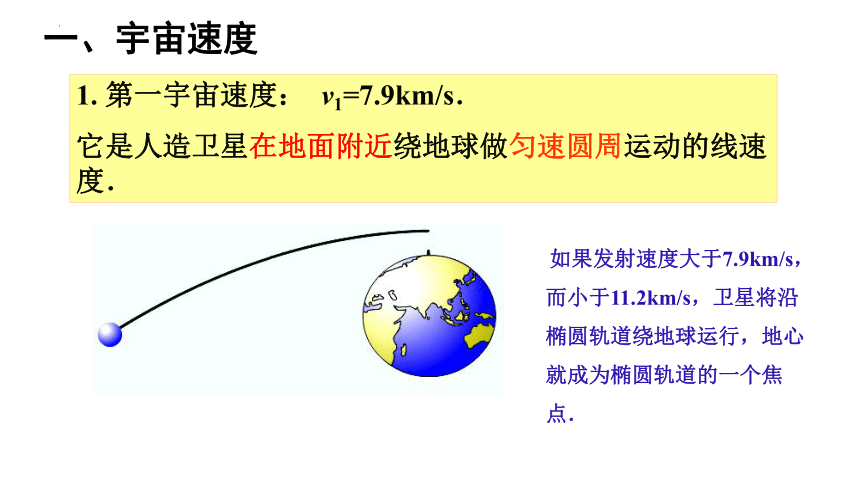
一、宇宙速度
1. 第一宇宙速度: v1=7.9km/s.
它是人造卫星在地面附近绕地球做匀速圆周运动的线速度.
如果发射速度大于7.9km/s,而小于11.2km/s,卫星将沿椭圆轨道绕地球运行,地心就成为椭圆轨道的一个焦点.
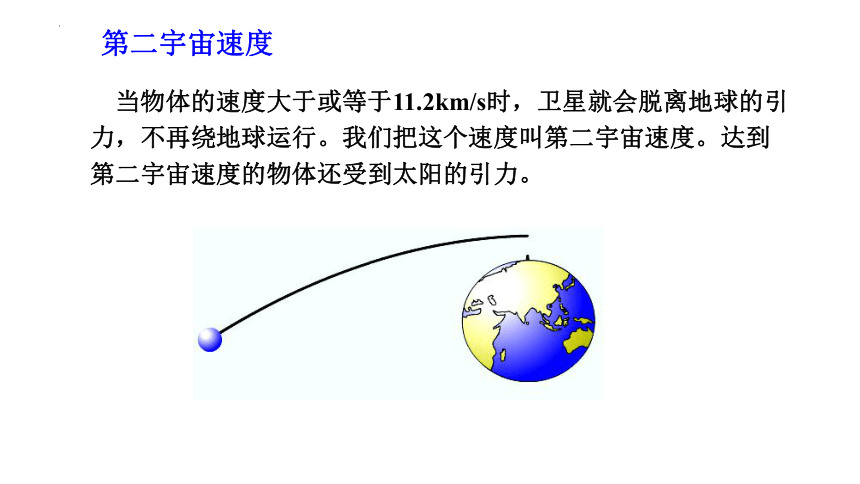
当物体的速度大于或等于11.2km/s时,卫星就会脱离地球的引力,不再绕地球运行。我们把这个速度叫第二宇宙速度。达到第二宇宙速度的物体还受到太阳的引力。
第二宇宙速度
如果物体的速度大于或等于16.7km/s,物体就摆脱了太阳引力的束缚,飞到太阳系以外的宇宙空间去。我们把这个速度叫第三宇宙速度。
第三宇宙速度
太阳
卫星指一些自然或人工的在太空中绕行星运动的物体。
在地球上抛出的物体,当它的速度足够大时,物体就永远不会落到地面上,它将围绕地球旋转,成为一颗绕地球运动的人造地球卫星,简称人造卫星。
人造地球卫星的发射设想图
v
平抛
洲际
导弹
人造
卫星
增大
发射速度足够大才能逃离地面;
发射人造地球卫星的最小速度有多大呢?
发射速度越大,卫星轨道离地表越远!
是否存在平行于其它纬度面的卫星轨道面?
二、人造卫星
O
1.所有人造卫星均有 F万=F向
2.所有人造卫星的轨道圆心都是地心
F
F向
F′
同步卫星轨道
地球同步卫星
1.定义:地球同步卫星是保持在地球赤道的地面上空、运行周期与地球的自转周期相同的人造地球卫星。
r
R
h
始终相对地面静止,
与地球自转“同步”
①轨道平面一定:赤道平面
②周期一定:地球自转周期24h
④角速度、线速度、向心加速度一定
③高度一定:
⑤绕行方向一定:与地球自转一致
同步卫星轨道
r
R
h
2.特点:
同步卫星通讯
单颗卫星信号所能覆盖的最大面积为地球表面的42%左右。故需要3颗同步卫星才能实现全球通讯。同步卫星只能分布在赤道正上方的一条圆弧上,为了卫星之间不相互干扰,大约3o左右才能放置一颗卫星。空间位置也是一种资源。
三、卫星变轨问题
V
F万
F万<F向
F万>F向
卫星变轨问题
M
m
A点速度—内小外大(在A点看轨迹)
在A点万有引力相同
A
F万 = F向
·
人造卫星从低轨道 高轨道的完整过程
在低轨道上加速,使其沿椭圆轨道运行,当行至椭圆轨道的远点处时再次加速,即可使其沿高轨道运行。
卫星在椭圆轨道运行
近地点---速度大,加速度大
远地点---速度小,加速度小
1
2
3
Q
P
卫星发射(1轨至3轨)示意图
vp2>vp1
vQ3>vQ2
v1>v3
vp2>vQ2
椭圆轨道:
第一次变轨:
第二次变轨:
圆轨道上稳定运行:
,aP2= aP1
,aQ3= aQ2
,aP2 > aQ2
, a1 > a3
周期呢?
P、Q位置实际加速度与向心加速度大小关系?
例2 2018年12月12日16时45分嫦娥四号探测器经过约110小时的奔月飞行到达月球附近。假设“嫦娥四号”在月球上空某高度处做圆周运动,运行速度为v1,为成功实施近月制动,使它进入更靠近月球的预定圆轨道,设其运行速度为v2。对这一变轨过程及变轨前后的速度对比正确的是( )
A.发动机向后喷气进入低轨道,v1>v2
B.发动机向后喷气进入低轨道,v1C.发动机向前喷气进入低轨道,v1>v2
D.发动机向前喷气进入低轨道,v1D
例3 如图所示为卫星发射过程的示意图,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再一次点火,将卫星送入同步圆轨道3. 轨道1、2相切于Q点,轨道2、3相切于P点,则当卫星分别在1、2、3轨道上正常运行时,以下说法中正确的是( )
A. 卫星在轨道3上的速率大于在轨道1上的速率
B. 卫星在轨道3上的周期大于在轨道2上的周期
C. 卫星在轨道1上经过Q点时的速率大于它在轨道2上
经过Q点时的速率
D. 卫星在轨道2上经过P点时的加速度小于它在轨道3
上经过P点时的加速度
B
例4 我国发射“中星9A”卫星,按预定计划,“中星9A”应该首先被送入近地点约为200公里,远地点约为3.6万公里的转移轨道Ⅱ(椭圆),然后通过在远地点变轨,进入最终同步轨道Ⅲ(圆形).但是由于火箭故障,卫星实际入轨后初始轨道Ⅰ远地点只有1.6万公里. 科技人员没有放弃,经过10次轨道调整,终于成功定点于预定轨道,如图所示.下列正确的是( )
A.“中星9A”发射失利原因可能是发射速度没有
达到7.9 km/s
B.卫星在轨道Ⅲ经过Q点时和在轨道Ⅱ经过Q点时
速度相同
C.卫星在轨道Ⅱ经过Q点的加速度大于它经过P点
时的加速度
D.卫星从轨道Ⅰ的P点进入轨道Ⅱ后速度增加
D
四、飞船对接问题
宇宙飞船与空间站的对接
空间站实际上就是一个载有人的人造卫星,那么,地球上的人如何到达空间站,空间站上的人又如何返回地面?这些活动都需要通过宇宙飞船来完成,这就存在一个宇宙飞船与空间站对接的问题。
思考:能否把宇宙飞船先发射到空间站的同一轨道上,再通过加速去追上空间站实现对接呢?
不行,因为飞船加速后做离心运动会偏离原来的圆轨道而无法与空间站对接。
如图示,飞船首先在比空间站低的轨道运行
当运行到适当位置时,再加速运行到一个椭圆轨道。
通过控制轨道使飞船跟空间站恰好同时运行到两轨道的相切点,此时飞船适当减速,便可实现对接。
空间站
飞船
对接方法:
从较低轨道加速去追及(对接)
例5 假设“天宫二号”与“神舟十一号”都围绕地球做匀速圆周运动,为了实现飞船与空间实验室的对接,下列措施可行的是( )
A.使飞船与空间实验室在同一轨道上运动,然后飞船加速追上空间实验室实现对接
B.使飞船与空间实验室在同一轨道上运行,然后空间实验室减速等待飞船实现对接
C.飞船先在比空间实验室半径小的轨道上加速,加速后飞船逐渐靠近空间实验室,两者速度接近时实现对接
D.飞船先在比空间实验室半径小的轨道上减速,减速后飞船逐渐靠近空间实验室,两者速度接近时实现对接
C
处理思路:
(1)根据=mrω2判断出谁的角速度大。
(2)若初始时刻,两星与天体在同一直线上,则内轨道所转过的圆心角与外轨道所转过的圆心角之差为π的整数倍时就是两星相距最近或相距最远的时刻。
(3)在分析卫星与地球上的物体的相遇与追及问题时,要根据地球上物体与同步卫星角速度相同的特点进行判断。
五、天体中的追及、相遇问题
例6 假设有一载人宇宙飞船在距地面高度为4200 km的赤道上空绕地球做匀速圆周运动,地球半径约为6400 km,地球同步卫星距地面高为36000 km,宇宙飞船和一地球同步卫星绕地球同向运动,每当两者相距最近时,宇宙飞船就向同步卫星发射信号,然后再由同步卫星将信号发送到地面接收站,某时刻两者相距最远,从此刻开始,在一昼夜的时间内,接收站共接收到信号的次数为( )
A.4次 B.6次
C.7次 D.8次
C
7.4 宇宙航行
提示:万有引力提供物体作匀速圆周运动的向心力。这个抛出速度就是做匀速圆周运动的线速度。
探究问题:以多大的速度抛出一个物体,它才会绕地球表面运动,不会落下来?(变成了近地卫星)
(已知G=6.67×10-11N·m2/kg2 , 地球质量M=5.98×1024kg, 地球半径R=6400km)
探究问题一 第一宇宙速度的推导
且 r = R
(地球近地卫星的线速度)
若不知道地球的质量M,只知道地球表面重力加速度g=9.8m/s2,R=6400km,又该如何计算?
地球表面附近,物体受到的重力等于地球对物体的引力,此时重力提供向心力
1.第一宇宙速度既是最小的发射速度,也是最大的环绕速度。
2.不同星体的第一宇宙速度不一样
(1)发射速度:指被发射物在地面附近离开发射装置时的初速度.
(2)运行速度:也叫环绕速度,是指卫星在进入运行轨道后绕地球做匀速圆周运动的线速度。
例1 我国发射了一颗绕月运行的探月卫星“嫦娥一号”。设该卫星的轨道是圆形的,且贴近月球表面,已知月球的质量约为地球质量的,月球的半径约为地球半径的,地球上的第一宇宙速度约为7.9 km/s,则该探月卫星绕月运行的最大速率约为( )
A.0.4 km/s B.1.8 km/s
C.11 km/s D.36 km/s
B
一、宇宙速度
1. 第一宇宙速度: v1=7.9km/s.
它是人造卫星在地面附近绕地球做匀速圆周运动的线速度.
如果发射速度大于7.9km/s,而小于11.2km/s,卫星将沿椭圆轨道绕地球运行,地心就成为椭圆轨道的一个焦点.
当物体的速度大于或等于11.2km/s时,卫星就会脱离地球的引力,不再绕地球运行。我们把这个速度叫第二宇宙速度。达到第二宇宙速度的物体还受到太阳的引力。
第二宇宙速度
如果物体的速度大于或等于16.7km/s,物体就摆脱了太阳引力的束缚,飞到太阳系以外的宇宙空间去。我们把这个速度叫第三宇宙速度。
第三宇宙速度
太阳
卫星指一些自然或人工的在太空中绕行星运动的物体。
在地球上抛出的物体,当它的速度足够大时,物体就永远不会落到地面上,它将围绕地球旋转,成为一颗绕地球运动的人造地球卫星,简称人造卫星。
人造地球卫星的发射设想图
v
平抛
洲际
导弹
人造
卫星
增大
发射速度足够大才能逃离地面;
发射人造地球卫星的最小速度有多大呢?
发射速度越大,卫星轨道离地表越远!
是否存在平行于其它纬度面的卫星轨道面?
二、人造卫星
O
1.所有人造卫星均有 F万=F向
2.所有人造卫星的轨道圆心都是地心
F
F向
F′
同步卫星轨道
地球同步卫星
1.定义:地球同步卫星是保持在地球赤道的地面上空、运行周期与地球的自转周期相同的人造地球卫星。
r
R
h
始终相对地面静止,
与地球自转“同步”
①轨道平面一定:赤道平面
②周期一定:地球自转周期24h
④角速度、线速度、向心加速度一定
③高度一定:
⑤绕行方向一定:与地球自转一致
同步卫星轨道
r
R
h
2.特点:
同步卫星通讯
单颗卫星信号所能覆盖的最大面积为地球表面的42%左右。故需要3颗同步卫星才能实现全球通讯。同步卫星只能分布在赤道正上方的一条圆弧上,为了卫星之间不相互干扰,大约3o左右才能放置一颗卫星。空间位置也是一种资源。
三、卫星变轨问题
V
F万
F万<F向
F万>F向
卫星变轨问题
M
m
A点速度—内小外大(在A点看轨迹)
在A点万有引力相同
A
F万 = F向
·
人造卫星从低轨道 高轨道的完整过程
在低轨道上加速,使其沿椭圆轨道运行,当行至椭圆轨道的远点处时再次加速,即可使其沿高轨道运行。
卫星在椭圆轨道运行
近地点---速度大,加速度大
远地点---速度小,加速度小
1
2
3
Q
P
卫星发射(1轨至3轨)示意图
vp2>vp1
vQ3>vQ2
v1>v3
vp2>vQ2
椭圆轨道:
第一次变轨:
第二次变轨:
圆轨道上稳定运行:
,aP2= aP1
,aQ3= aQ2
,aP2 > aQ2
, a1 > a3
周期呢?
P、Q位置实际加速度与向心加速度大小关系?
例2 2018年12月12日16时45分嫦娥四号探测器经过约110小时的奔月飞行到达月球附近。假设“嫦娥四号”在月球上空某高度处做圆周运动,运行速度为v1,为成功实施近月制动,使它进入更靠近月球的预定圆轨道,设其运行速度为v2。对这一变轨过程及变轨前后的速度对比正确的是( )
A.发动机向后喷气进入低轨道,v1>v2
B.发动机向后喷气进入低轨道,v1
D.发动机向前喷气进入低轨道,v1
例3 如图所示为卫星发射过程的示意图,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再一次点火,将卫星送入同步圆轨道3. 轨道1、2相切于Q点,轨道2、3相切于P点,则当卫星分别在1、2、3轨道上正常运行时,以下说法中正确的是( )
A. 卫星在轨道3上的速率大于在轨道1上的速率
B. 卫星在轨道3上的周期大于在轨道2上的周期
C. 卫星在轨道1上经过Q点时的速率大于它在轨道2上
经过Q点时的速率
D. 卫星在轨道2上经过P点时的加速度小于它在轨道3
上经过P点时的加速度
B
例4 我国发射“中星9A”卫星,按预定计划,“中星9A”应该首先被送入近地点约为200公里,远地点约为3.6万公里的转移轨道Ⅱ(椭圆),然后通过在远地点变轨,进入最终同步轨道Ⅲ(圆形).但是由于火箭故障,卫星实际入轨后初始轨道Ⅰ远地点只有1.6万公里. 科技人员没有放弃,经过10次轨道调整,终于成功定点于预定轨道,如图所示.下列正确的是( )
A.“中星9A”发射失利原因可能是发射速度没有
达到7.9 km/s
B.卫星在轨道Ⅲ经过Q点时和在轨道Ⅱ经过Q点时
速度相同
C.卫星在轨道Ⅱ经过Q点的加速度大于它经过P点
时的加速度
D.卫星从轨道Ⅰ的P点进入轨道Ⅱ后速度增加
D
四、飞船对接问题
宇宙飞船与空间站的对接
空间站实际上就是一个载有人的人造卫星,那么,地球上的人如何到达空间站,空间站上的人又如何返回地面?这些活动都需要通过宇宙飞船来完成,这就存在一个宇宙飞船与空间站对接的问题。
思考:能否把宇宙飞船先发射到空间站的同一轨道上,再通过加速去追上空间站实现对接呢?
不行,因为飞船加速后做离心运动会偏离原来的圆轨道而无法与空间站对接。
如图示,飞船首先在比空间站低的轨道运行
当运行到适当位置时,再加速运行到一个椭圆轨道。
通过控制轨道使飞船跟空间站恰好同时运行到两轨道的相切点,此时飞船适当减速,便可实现对接。
空间站
飞船
对接方法:
从较低轨道加速去追及(对接)
例5 假设“天宫二号”与“神舟十一号”都围绕地球做匀速圆周运动,为了实现飞船与空间实验室的对接,下列措施可行的是( )
A.使飞船与空间实验室在同一轨道上运动,然后飞船加速追上空间实验室实现对接
B.使飞船与空间实验室在同一轨道上运行,然后空间实验室减速等待飞船实现对接
C.飞船先在比空间实验室半径小的轨道上加速,加速后飞船逐渐靠近空间实验室,两者速度接近时实现对接
D.飞船先在比空间实验室半径小的轨道上减速,减速后飞船逐渐靠近空间实验室,两者速度接近时实现对接
C
处理思路:
(1)根据=mrω2判断出谁的角速度大。
(2)若初始时刻,两星与天体在同一直线上,则内轨道所转过的圆心角与外轨道所转过的圆心角之差为π的整数倍时就是两星相距最近或相距最远的时刻。
(3)在分析卫星与地球上的物体的相遇与追及问题时,要根据地球上物体与同步卫星角速度相同的特点进行判断。
五、天体中的追及、相遇问题
例6 假设有一载人宇宙飞船在距地面高度为4200 km的赤道上空绕地球做匀速圆周运动,地球半径约为6400 km,地球同步卫星距地面高为36000 km,宇宙飞船和一地球同步卫星绕地球同向运动,每当两者相距最近时,宇宙飞船就向同步卫星发射信号,然后再由同步卫星将信号发送到地面接收站,某时刻两者相距最远,从此刻开始,在一昼夜的时间内,接收站共接收到信号的次数为( )
A.4次 B.6次
C.7次 D.8次
C
