北京重点大学附属中学2023—2024学年下学期九年级开学考试数学试题(无答案)
文档属性
| 名称 | 北京重点大学附属中学2023—2024学年下学期九年级开学考试数学试题(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-09 00:00:00 | ||
图片预览



文档简介
北京重点大学附属中学2023—2024学年下学期九年级开学考试数学试题
一、选择题(共16分,每题2分)第1-8题均有四个选项,符合题意的选项只有一个.
1.下列四个图形中,既是轴对称图形又是中心对称图形的是( )
2.若x=3是一元二次方程x -2x+m=0的一个根,则m的值是( )
A.-3 B. -15 C. 3 D.15
3.如图,在Rt△ACB中,∠C=90°,AC=3BC,则tanA为( )
A. B. C. D.
第3题图 第5题图
4.如果将抛物线y=x 向上平移3个单位长度,向左平移1各单位,得到新的抛物线的表达式是( )
A.y=(x+1) -3 B.y=(x+1) +3 C.y=(x-1) -3 D.y=(x-1) +3
5.如图,四边形ABCD内接于⊙O,AB是直径,D是的中点.若∠B=40°,则∠A的大小为( )
A.50° B.60° C. 70° D.80°
6.《2024年春节联欢晚会》以匠心独运的歌舞创编、暖心真挚的节目表演、充满科技感和时代感的视觉呈现,为海内外受众奉上了一道心意满满、暖意融融的除夕“文化大餐”。截至2月10日2时,总台春晚全媒体累计触达142亿人次,其中“竖屏看春晚”直播播放量4.2亿次.据统计,2022年首次推出的“竖屏看春晚”累计观看2亿次,设“竖屏看春晚”次数的年平均增长率为x,则可列出关于x的方程( )
A.4.2(1+x) =142 B.2(1+x) =4.2 C.2(1+2x)=4.2 D.4.2(1-x) =2
7.在平面直角坐标系xOy中,若点(0,y1),(4,y )在抛物线y=a(x-3) +1(a>0)上,则下列结论正确的是()
A.18.如图,正方形ABCD的边长为2,点E是AB上一动点(点E与点A,B不重合),点F在BC延长线上,AE=CF,以BE,BF为边作矩形BEGF.设AE的长为x,矩形BEGF的面积为y,则y与x满足的函数关系的图象是
二、填空题(共16分,每题2分)
9.已知反比例函数y=(k是常数,且k≠2)的图象有一支在第三象限,那么k的取值范围是___.
10.抛物线y=x +2x-3的顶点坐标是______
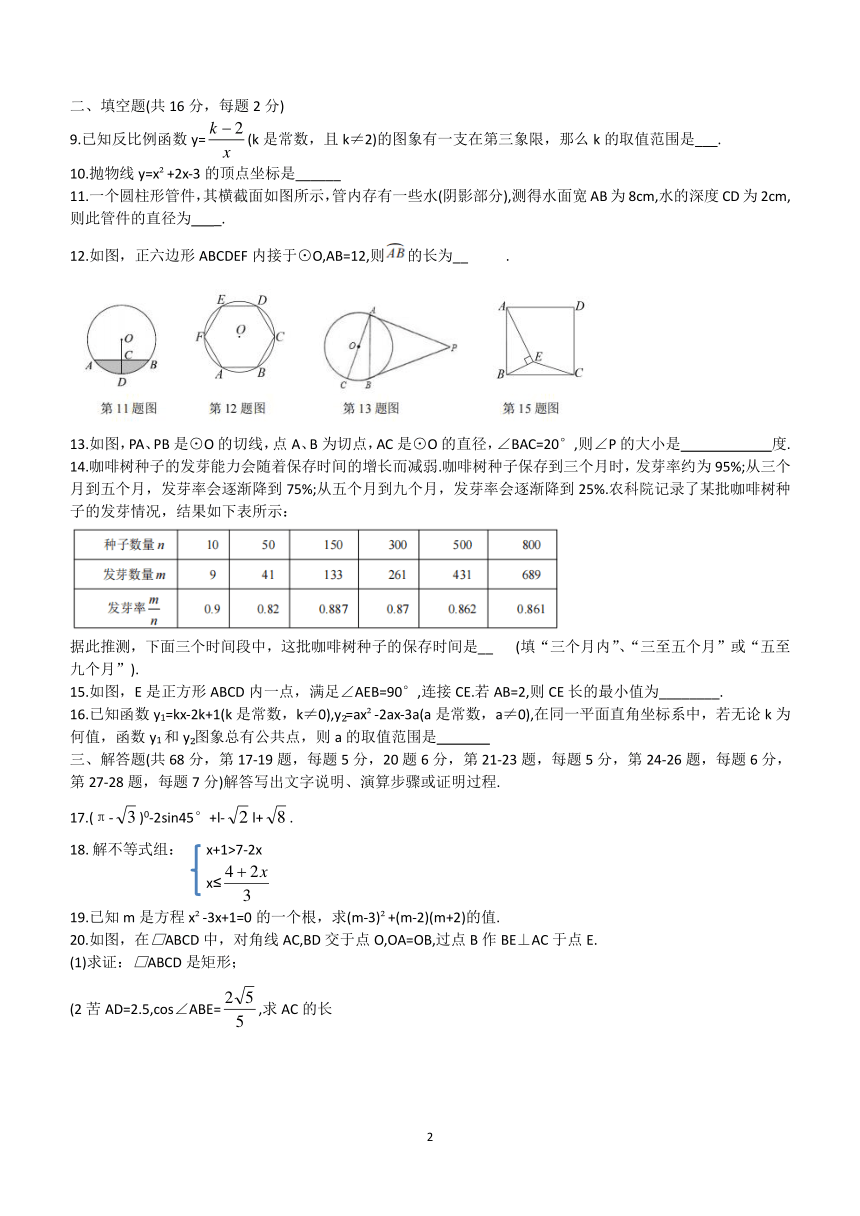
11.一个圆柱形管件,其横截面如图所示,管内存有一些水(阴影部分),测得水面宽AB为8cm,水的深度CD为2cm,则此管件的直径为 _.
12.如图,正六边形ABCDEF内接于⊙O,AB=12,则的长为__ .
13.如图,PA、PB是⊙O的切线,点A、B为切点,AC是⊙O的直径,∠BAC=20°,则∠P的大小是 度.
14.咖啡树种子的发芽能力会随着保存时间的增长而减弱.咖啡树种子保存到三个月时,发芽率约为95%;从三个月到五个月,发芽率会逐渐降到75%;从五个月到九个月,发芽率会逐渐降到25%.农科院记录了某批咖啡树种子的发芽情况,结果如下表所示:
据此推测,下面三个时间段中,这批咖啡树种子的保存时间是__ (填“三个月内”、“三至五个月”或“五至九个月”).
15.如图,E是正方形ABCD内一点,满足∠AEB=90°,连接CE.若AB=2,则CE长的最小值为________.
16.已知函数y1=kx-2k+1(k是常数,k≠0),y =ax -2ax-3a(a是常数,a≠0),在同一平面直角坐标系中,若无论k为何值,函数y1和y 图象总有公共点,则a的取值范围是
三、解答题(共68分,第17-19题,每题5分,20题6分,第21-23题,每题5分,第24-26题,每题6分,第27-28题,每题7分)解答写出文字说明、演算步骤或证明过程.
17.(π-)0-2sin45°+l-l+.
解不等式组: x+1>7-2x
x≤
19.已知m是方程x -3x+1=0的一个根,求(m-3) +(m-2)(m+2)的值.
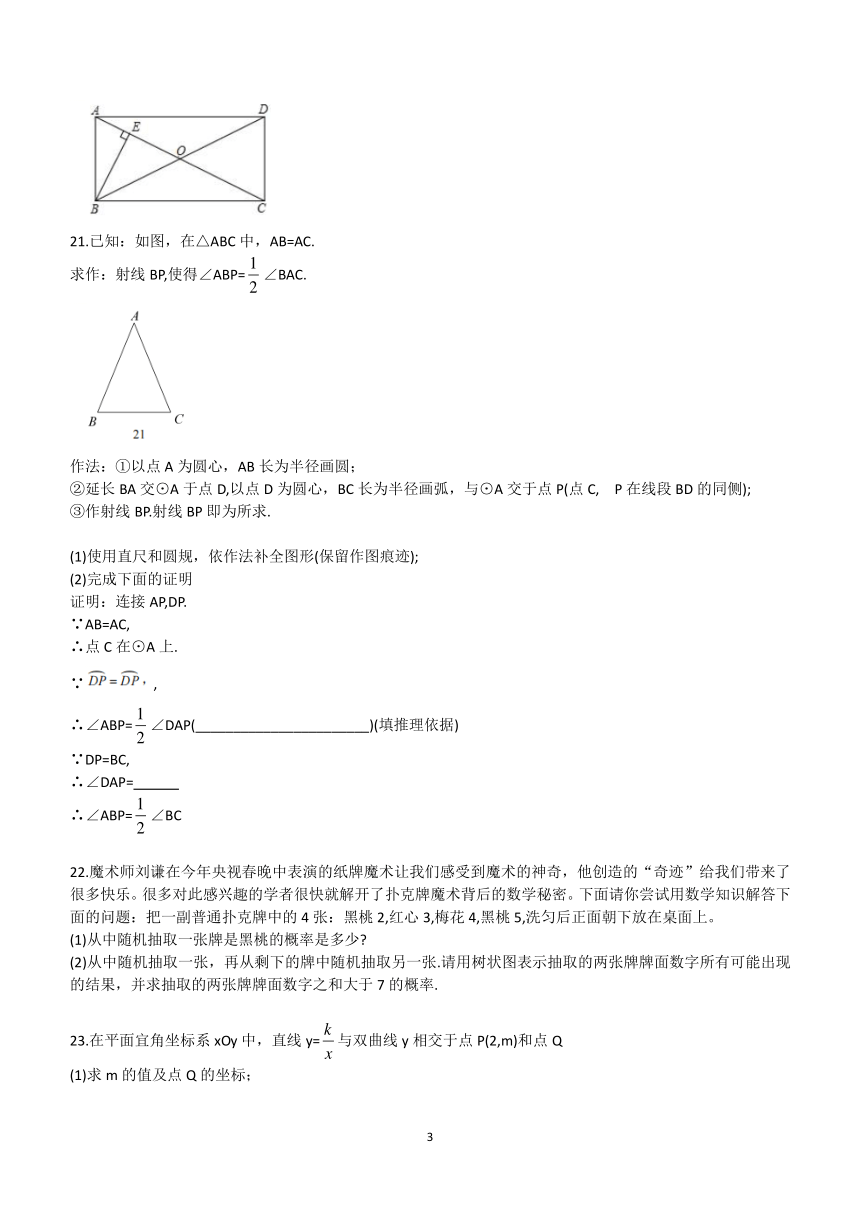
20.如图,在□ABCD中,对角线AC,BD交于点O,OA=OB,过点B作BE⊥AC于点E.
(1)求证:□ABCD是矩形;
(2苦AD=2.5,cos∠ABE=,求AC的长
21.已知:如图,在△ABC中,AB=AC.
求作:射线BP,使得∠ABP=∠BAC.
作法:①以点A为圆心,AB长为半径画圆;
②延长BA交⊙A于点D,以点D为圆心,BC长为半径画弧,与⊙A交于点P(点C, P在线段BD的同侧);
③作射线BP.射线BP即为所求.
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);
(2)完成下面的证明
证明:连接AP,DP.
∵AB=AC,
∴点C在⊙A上.
∵,
∴∠ABP=∠DAP(_______________________)(填推理依据)
∵DP=BC,
∴∠DAP=
∴∠ABP=∠BC
22.魔术师刘谦在今年央视春晚中表演的纸牌魔术让我们感受到魔术的神奇,他创造的“奇迹”给我们带来了很多快乐。很多对此感兴趣的学者很快就解开了扑克牌魔术背后的数学秘密。下面请你尝试用数学知识解答下面的问题:把一副普通扑克牌中的4张:黑桃2,红心3,梅花4,黑桃5,洗匀后正面朝下放在桌面上。
(1)从中随机抽取一张牌是黑桃的概率是多少
(2)从中随机抽取一张,再从剩下的牌中随机抽取另一张.请用树状图表示抽取的两张牌牌面数字所有可能出现的结果,并求抽取的两张牌牌面数字之和大于7的概率.
23.在平面宜角坐标系xOy中,直线y=与双曲线y相交于点P(2,m)和点Q
(1)求m的值及点Q的坐标;
(2)已知点N(0,n),过点N作平行于x轴的直线交直线)y=x与双曲线y=分别为点A(x ,y )和B(x ,y ).当x >x 时,根据函数图象,直接写出n的取值范围是________.
24.某校组织九年级学生参加社会实践活动,数学学科的项目任务是测量银山塔林中某塔的高度AB,其中一个数学兴趣小组设计的方案如图所示,他们在点C处用高1.5m的测角仪CD测得塔顶A的仰角为37°,然后沿CB方向前行7m到达点F处,在F处测得塔顶A的仰角为45°.请根据他们的测量数据求塔高AB的长度大约是多少.(参考数据:sin37°≈,cos37°≈,tan37°≈,sin53°≈,cos53°≈号,tan53°≈)
25.如图,AB为⊙O的直径,点C在⊙O上,∠ACB的平分线CD交⊙O于点D. 过点D作DE//AB,交CB的延长线于点E.
(1)求证:直线DE是⊙O的切线;
(2)若BC=OA=,求BE的长.
26.在平面直角坐标系xOy中,点(x ,y1),(x ,y )在抛物线y=x -2mx-3上,m(1)若点(2,-3)在抛物线上,求m的值.
(2)若对于任意的x1,x ,总有y >y1,求m的取值范围.
27.如图,在△ABC中,∠BAC=90°,AB=AC,AD是BC边上的高,点E是边AB上的一动点(不与点A,B重合),连接CE交AD于点F,将线段CF绕点C顺时针旋转90°得到线段CG,连接AG.
如图1,当CE是∠ACB的角平分线时,
①求证:AE =AF;
②直接写出∠CAG =__ °.
(2) 依题意补全图2,用等式表示线段AF,AC,AG之间的数量关系,并证明.
28.(7分)在平面直角坐标系xOy中,⊙O的半径为1,A为任意一点,B为⊙O上任意一点.给出如下定义:记A,B两点间的距离的最小值为p(规定:点A在⊙O上时,p=0),最大值为q,那么把的值称为点A与⊙O的“关联距离”,记作d(A,⊙O).
(1)如图,点D,E,F的横、纵坐标都是整数.
①d(D.⊙O)=
②若点M在线段EF上,求d(M,⊙O)的取值范围;
(2)若点N在直线y=x+2上,直接写出d(N,⊙O)的取值范围;
(3)正方形的边长为m,若点P在该正方形的边上运动时,满足d(P,⊙O)的最小值为1,最大值为,直接写出m的最小值和最大值.
一、选择题(共16分,每题2分)第1-8题均有四个选项,符合题意的选项只有一个.
1.下列四个图形中,既是轴对称图形又是中心对称图形的是( )
2.若x=3是一元二次方程x -2x+m=0的一个根,则m的值是( )
A.-3 B. -15 C. 3 D.15
3.如图,在Rt△ACB中,∠C=90°,AC=3BC,则tanA为( )
A. B. C. D.
第3题图 第5题图
4.如果将抛物线y=x 向上平移3个单位长度,向左平移1各单位,得到新的抛物线的表达式是( )
A.y=(x+1) -3 B.y=(x+1) +3 C.y=(x-1) -3 D.y=(x-1) +3
5.如图,四边形ABCD内接于⊙O,AB是直径,D是的中点.若∠B=40°,则∠A的大小为( )
A.50° B.60° C. 70° D.80°
6.《2024年春节联欢晚会》以匠心独运的歌舞创编、暖心真挚的节目表演、充满科技感和时代感的视觉呈现,为海内外受众奉上了一道心意满满、暖意融融的除夕“文化大餐”。截至2月10日2时,总台春晚全媒体累计触达142亿人次,其中“竖屏看春晚”直播播放量4.2亿次.据统计,2022年首次推出的“竖屏看春晚”累计观看2亿次,设“竖屏看春晚”次数的年平均增长率为x,则可列出关于x的方程( )
A.4.2(1+x) =142 B.2(1+x) =4.2 C.2(1+2x)=4.2 D.4.2(1-x) =2
7.在平面直角坐标系xOy中,若点(0,y1),(4,y )在抛物线y=a(x-3) +1(a>0)上,则下列结论正确的是()
A.1
二、填空题(共16分,每题2分)
9.已知反比例函数y=(k是常数,且k≠2)的图象有一支在第三象限,那么k的取值范围是___.
10.抛物线y=x +2x-3的顶点坐标是______
11.一个圆柱形管件,其横截面如图所示,管内存有一些水(阴影部分),测得水面宽AB为8cm,水的深度CD为2cm,则此管件的直径为 _.
12.如图,正六边形ABCDEF内接于⊙O,AB=12,则的长为__ .
13.如图,PA、PB是⊙O的切线,点A、B为切点,AC是⊙O的直径,∠BAC=20°,则∠P的大小是 度.
14.咖啡树种子的发芽能力会随着保存时间的增长而减弱.咖啡树种子保存到三个月时,发芽率约为95%;从三个月到五个月,发芽率会逐渐降到75%;从五个月到九个月,发芽率会逐渐降到25%.农科院记录了某批咖啡树种子的发芽情况,结果如下表所示:
据此推测,下面三个时间段中,这批咖啡树种子的保存时间是__ (填“三个月内”、“三至五个月”或“五至九个月”).
15.如图,E是正方形ABCD内一点,满足∠AEB=90°,连接CE.若AB=2,则CE长的最小值为________.
16.已知函数y1=kx-2k+1(k是常数,k≠0),y =ax -2ax-3a(a是常数,a≠0),在同一平面直角坐标系中,若无论k为何值,函数y1和y 图象总有公共点,则a的取值范围是
三、解答题(共68分,第17-19题,每题5分,20题6分,第21-23题,每题5分,第24-26题,每题6分,第27-28题,每题7分)解答写出文字说明、演算步骤或证明过程.
17.(π-)0-2sin45°+l-l+.
解不等式组: x+1>7-2x
x≤
19.已知m是方程x -3x+1=0的一个根,求(m-3) +(m-2)(m+2)的值.
20.如图,在□ABCD中,对角线AC,BD交于点O,OA=OB,过点B作BE⊥AC于点E.
(1)求证:□ABCD是矩形;
(2苦AD=2.5,cos∠ABE=,求AC的长
21.已知:如图,在△ABC中,AB=AC.
求作:射线BP,使得∠ABP=∠BAC.
作法:①以点A为圆心,AB长为半径画圆;
②延长BA交⊙A于点D,以点D为圆心,BC长为半径画弧,与⊙A交于点P(点C, P在线段BD的同侧);
③作射线BP.射线BP即为所求.
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);
(2)完成下面的证明
证明:连接AP,DP.
∵AB=AC,
∴点C在⊙A上.
∵,
∴∠ABP=∠DAP(_______________________)(填推理依据)
∵DP=BC,
∴∠DAP=
∴∠ABP=∠BC
22.魔术师刘谦在今年央视春晚中表演的纸牌魔术让我们感受到魔术的神奇,他创造的“奇迹”给我们带来了很多快乐。很多对此感兴趣的学者很快就解开了扑克牌魔术背后的数学秘密。下面请你尝试用数学知识解答下面的问题:把一副普通扑克牌中的4张:黑桃2,红心3,梅花4,黑桃5,洗匀后正面朝下放在桌面上。
(1)从中随机抽取一张牌是黑桃的概率是多少
(2)从中随机抽取一张,再从剩下的牌中随机抽取另一张.请用树状图表示抽取的两张牌牌面数字所有可能出现的结果,并求抽取的两张牌牌面数字之和大于7的概率.
23.在平面宜角坐标系xOy中,直线y=与双曲线y相交于点P(2,m)和点Q
(1)求m的值及点Q的坐标;
(2)已知点N(0,n),过点N作平行于x轴的直线交直线)y=x与双曲线y=分别为点A(x ,y )和B(x ,y ).当x >x 时,根据函数图象,直接写出n的取值范围是________.
24.某校组织九年级学生参加社会实践活动,数学学科的项目任务是测量银山塔林中某塔的高度AB,其中一个数学兴趣小组设计的方案如图所示,他们在点C处用高1.5m的测角仪CD测得塔顶A的仰角为37°,然后沿CB方向前行7m到达点F处,在F处测得塔顶A的仰角为45°.请根据他们的测量数据求塔高AB的长度大约是多少.(参考数据:sin37°≈,cos37°≈,tan37°≈,sin53°≈,cos53°≈号,tan53°≈)
25.如图,AB为⊙O的直径,点C在⊙O上,∠ACB的平分线CD交⊙O于点D. 过点D作DE//AB,交CB的延长线于点E.
(1)求证:直线DE是⊙O的切线;
(2)若BC=OA=,求BE的长.
26.在平面直角坐标系xOy中,点(x ,y1),(x ,y )在抛物线y=x -2mx-3上,m
(2)若对于任意的x1,x ,总有y >y1,求m的取值范围.
27.如图,在△ABC中,∠BAC=90°,AB=AC,AD是BC边上的高,点E是边AB上的一动点(不与点A,B重合),连接CE交AD于点F,将线段CF绕点C顺时针旋转90°得到线段CG,连接AG.
如图1,当CE是∠ACB的角平分线时,
①求证:AE =AF;
②直接写出∠CAG =__ °.
(2) 依题意补全图2,用等式表示线段AF,AC,AG之间的数量关系,并证明.
28.(7分)在平面直角坐标系xOy中,⊙O的半径为1,A为任意一点,B为⊙O上任意一点.给出如下定义:记A,B两点间的距离的最小值为p(规定:点A在⊙O上时,p=0),最大值为q,那么把的值称为点A与⊙O的“关联距离”,记作d(A,⊙O).
(1)如图,点D,E,F的横、纵坐标都是整数.
①d(D.⊙O)=
②若点M在线段EF上,求d(M,⊙O)的取值范围;
(2)若点N在直线y=x+2上,直接写出d(N,⊙O)的取值范围;
(3)正方形的边长为m,若点P在该正方形的边上运动时,满足d(P,⊙O)的最小值为1,最大值为,直接写出m的最小值和最大值.
同课章节目录
