2015-2016年安徽省宣城市孙埠中学第21章 二次函数与反比例函数检测题及答案解析
文档属性
| 名称 | 2015-2016年安徽省宣城市孙埠中学第21章 二次函数与反比例函数检测题及答案解析 |
|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-01 00:00:00 | ||
图片预览





文档简介
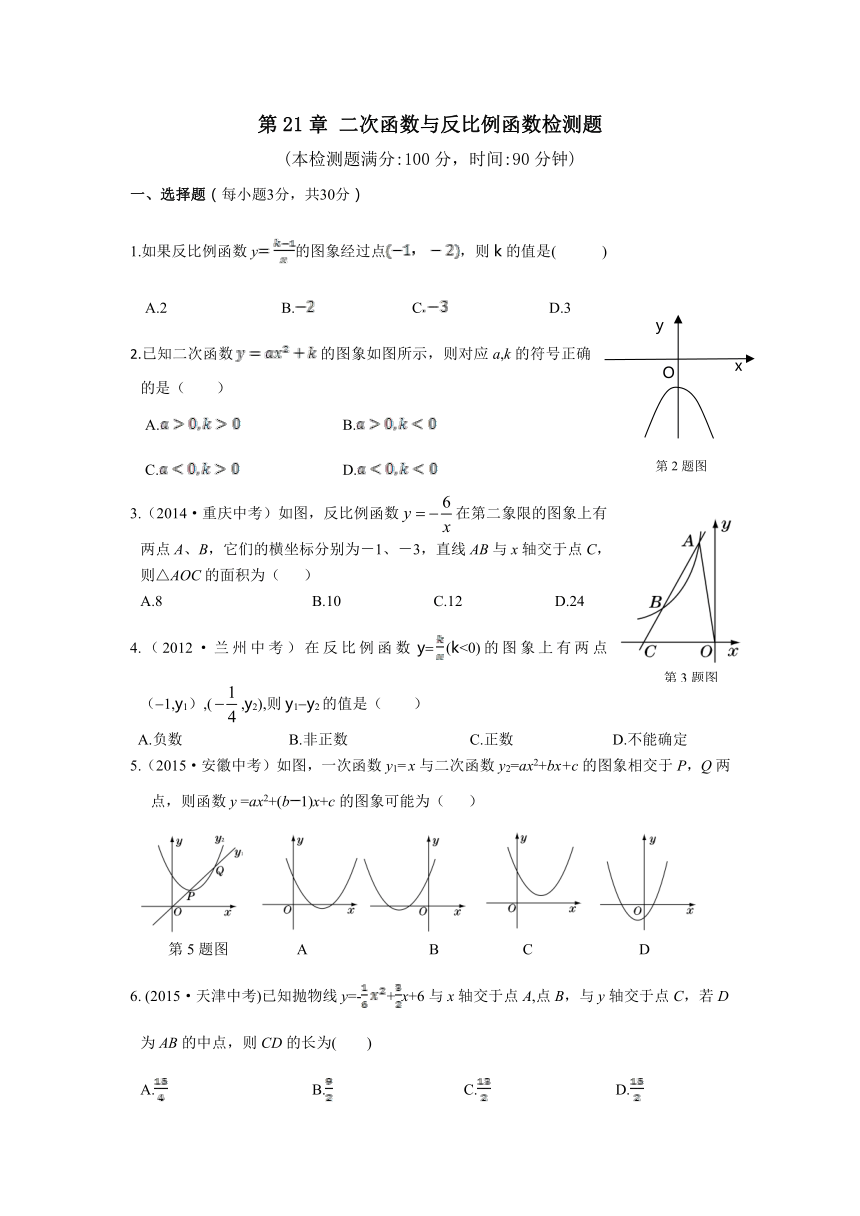
第21章 二次函数与反比例函数检测题
(本检测题满分:100分,时间:90分钟)
一、选择题(每小题3分,共30分)
1.如果反比例函数y的图象经过点,则k的值是( )
A.2 B. C D.3
2.已知二次函数的图象如图所示,则对应a,k的符号正确的是( )
A. B.
C. D.
3.(2014·重庆中考)如图,反比例函数在第二象限的图象上有两点A、B,它们的横坐标分别为-1、-3,直线AB与x轴交于点C,则△AOC的面积为( )
A.8 B.10 C.12 D.24
4.(2012·兰州中考)在反比例函数y (k<0)的图象上有两点( 1,y1),(,y2),则y1 y2的值是( )
A.负数 B.非正数 C.正数 D.不能确定
5.(2015·安徽中考)如图,一次函数y1= x与二次函数y2=ax2+bx+c的图象相交于P,Q两点,则函数y =ax2+(b1)x+c的图象可能为( )
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
第5题图 A B C D
6. (2015·天津中考)已知抛物线y=-+x+6与x轴交于点A,点B,与y轴交于点C,若D为AB的中点,则CD的长为( )
A. B. C. D.
7. 如图,A为反比例函数图象上一点,AB垂直轴于点B,若S△AOB=3,则的值为 ( )
A.6 B.3
C. D.不能确定
8.已知M、N两点关于y轴对称,且点M在双曲线y 上,点N在直线y x 3上,设点M的坐标为(a,b),则二次函数y abx2 (a b)x( )
A.有最大值,最大值为B.有最大值,最大值为
C.有最小值,最小值为 D.有最小值,最小值为
9.(2015·湖北孝感中考)如图 ,二次函数yax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:
①abc<0;②0;③ac-b+10;④OA·OB=.
其中正确结论的个数是( )
( http: / / www.21cnjy.com )
第9题图
A.4 B.3 C.2 D.1
10.在函数(a为常数)的图象上有三点( 3,y1),( 1,y2),(2,y3),则函数值y1,y2,y3的大小关系是( )
A. B.
C. D.
二、填空题(每小题3分,共24分)
11.点P在反比例函数y (k≠0)的图象上,点Q(2,4)与点P关于y轴对称,则此反比例函数的关系式为 .
12. 将抛物线向右平移2个单位后,再向下平移5个单位,所得抛物线的顶点坐标为_______.
13.试写出图象位于第二、四象限的一个反比例函数的关系式 .
14.若反比例函数的图象位于第一、三象限,正比例函数的图象过第二、四象限,则的整数值是________.
15.抛物线在轴上截得的线段长度是 .
16.设三点依次分别是抛物线与轴的交点以及与轴的两个交点,则△的面积是 .
17.把二次函数y (x-1)2 2的图象绕原点旋转180°后得到的图象的关系式为 .
18.若M(2,2)和N(b, 1 n2)是反比例函数y 图象上的两点,则一次函数y kx b的图象经过第 象限.
三、解答题(共46分)
19.(6分)(2014·北京中考)在平面直角坐标系中,抛物线经过点A(0, -2),B(3, 4).
(1)求抛物线的表达式及对称轴;
(2)设点B关于原点的对称点为C,点D是 ( http: / / www.21cnjy.com )抛物线对称轴上一动点,记抛物线在A,B之间的部分为图象G(包含A, B两点).若直线CD与图象G有公共点,结合函数图象,求点D纵坐标t的取值范围.
20.(6分)如图所示,一个运动员推铅球,铅球在点A处出手,出手时球离地面约.铅球落地点在B处,铅球运行中在运动员前4 m处(即 m)达到最高点,最高点高3 m.已知铅球经过的路线是抛物线,根据图示的直角坐标系,你能算出该运动员的成绩吗
21.(6分)(2015·贵州安顺中考)如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=的图象交于A(2,3)、B(-3,n)两点.
( http: / / www.21cnjy.com )
第21题图
(1)求一次函数和反比例函数的解析式;
(2)若P是y轴上一点,且满足△PAB的面积是5,直接写出OP的长.
22.(7分)如图,已知直线与轴、轴分别交于点A、B,与反比例函数 ()的图象分别交于点C、D,且点C的坐标为(,2).
(1)分别求出直线AB及反比例函数的关 系式;
(2)求出点D的坐标;
(3)利用图象直接写出:当x在什么范围内取值时,>.
23.(7分)已知函数的图象经过点(3,2).
(1)求这个函数的关系式;
(2)画出它的图象,并指出图象的顶点坐标;
(3)当时,求使得的的取值范围.
24.(7分)(2015 湖北襄阳中考)为 ( http: / / www.21cnjy.com )满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌粽子,每盒进价是40元,超市规定每盒售价不得少于45元.根据以往销售经验发现:当售价定为每盒45元时,每天可卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;
(2)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?
(3)为稳定物价,有关管理部门限定:这种粽 ( http: / / www.21cnjy.com )子的每盒售价不得高于58元.如果超市想要每天获得不低于6 000元的利润,那么超市每天至少销售粽子多少盒?
25.(7分)(2015·山东青岛中考)如图,隧道的截面由抛物线和长方形构成,长方形的长是12 m,宽是4 m.按照图中所示的直角坐标系,抛物线可以用表示,且抛物线上的点C到墙面OB的水平距离为3 m,到地面OA的距离为m.
(1)求该抛物线的函数关系式,并计算出拱顶D到地面OA的距离.
(2)一辆货运汽车载一长方体集装箱后高为6 m,宽为4 m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8 m,那么两排灯的水平距离最小是多少米?
( http: / / www.21cnjy.com )
第25题图
第21章 二次函数与反比例函数检测题参考答案
一、选择题
1.D 解析:把代入得-2=,∴ k 3.
2. D 解析:二次函数的图象开口向上时开口向下时图象交于y 轴正半轴时交于y轴负半轴时
3.C 解析: ∵ 点A、B都在反比例函数的图象上,∴ A(-1,6),B(-3,2).设直线AB的表达式为,则解得
∴ 直线AB的表达式为,∴ C(-4,0).在△中,OC=4,OC边上的高(即点A到x轴的距离)为6,∴ △的面积在平面直角坐标系中求三角形的面积时,一般要将落在坐标轴上的一边作为底.
4. A 解析:由题意知y1 k,y2 4k.∵ k<0,∴ y1-y2 -k-(-4k) 3k<0.
5.A 解析:一次函数 ( http: / / www.21cnjy.com )y1=x与二次函数y2=ax2+bx+c的图象有两个交点,且都在第一象限,可知一元二次方程ax2+bx+c=x,即ax2+(b-1)x+c=0有两个不相等的正实数根,所以函数y=ax2+(b-1)x+c的图象与x轴的正半轴有两个不同的交点,故选项A符合题意.
6. D 解析:令y=0,即-+x+6=0,解得=-3,=12,所以A、B两点的坐标为(-3,0)、(12,0),所以点D的横坐标为x==,所以OD=(O为坐标原点).因为抛物线与y轴交于点C,所以点C的坐标为(0,6),所以OC=6.在Rt△COD中,CD===.故选D.
7.A 解析:设A点的坐标为,则OB a,AB ,则
则k 6.
8.B 解析:∵ 点M的坐标为(a,b),∴ 点N的坐标为(-a,b).
∵ 点M在双曲线y 上,∴ ab .
∵ 点N(-a,b)在直线y x 3上,∴ -a 3 b.∴ a b 3.
∴ 二次函数y -abx2 (a b)x x2 3x (x-3)2 .
∴ 二次函数y -abx2 (a b)x有最大值,最大值为.
9.B 解析:因为抛物线开口向下,与y轴交于正半轴,对称轴x>0,且与x轴有两个交点,所以a<0,b>0,c>0,>0,所以abc<0,<0,故①正确,②错误.
因为OA=OC,所以点A的坐标可表示为(-c,0),代入解析式得,所以,故③正确.
设点A、B的坐标分别为(),(),所以是方程的两根,所以.又OA=-,OB=,所以,故④正确.所以①③④正确.
10. D 解析:是反比例函数,且,
∴ 双曲线的图象在第二、四象限,在各个象限内,y随x的增大而增大.
和在第二象限,且,∴ 0<y1<y2.
又∵ 点(2,y3)在第四象限,∴ y3<0.
因此y1,y2,y3的大小关系是y3<y1<y2.
二、填空题
11.y 解析:设点P(x,y),∵ 点P与点Q(2,4)关于y轴对称,则P,4),
∴ kxy2×4 -8.∴ y .
12.
13. 答案不唯一,如 解析:设反比例函数的关系式为y ,∵ 反比例函数的图象位于第二、四象限,∴ k 0,据此写出一个函数关系式即可,如k -1,则.
14.4 解析:由反比例函数的图象位于第一、三象限,得,即.又正比例函数的图象过第二、四象限,所以,所以.所以的整数值是4.
15.4 解析:由得,所以抛物线在轴上截得的线段长度是.
16. 解析:令,令,得,
所以,
所以△的面积是.
17.y -(x 1)2-2 解析:抛物线绕原点旋转180°后,开口方向与原抛物线开口方向相反,开口大小不变,顶点坐标变为),
∴ 旋转180°后得到的函数图象的关系式为y -(x 1)2-2.
18.一、三、四 解析:把M(2,2)代入y 得2 ,解得k 4.
把N(b,-1-n2)代入y 得-1-n2 ,即﹣(1 n2) ,∴ b<0,
∴ y kx b中,k 4>0,b<0,∴ 图象经过第一、三、四象限.
三、解答题
19.解:(1)∵ 经过点A(0,-2),B(3,4),
代入得∴
∴ 抛物线的表达式为
∴ 其对称轴为直线x=-1.
(2)由题意可知C(-3,-4),二次函数的最小值为-4.
( http: / / www.21cnjy.com )
第19题答图
由图象可以看出D点纵坐标最小值即为-4,
最大值即BC与对称轴交点的纵坐标.
设直线BC的函数表达式为y=kx b,
根据题意得解得
∴ 直线BC的函数表达式为
当x=1时,
∴ 点D纵坐标t的取值范围是
20.解:能.∵ OC=4 m,CD=3 m,,∴ 顶点的坐标为(4,3).
设 3,
把代入上式,得 ,∴,
∴ 即.
令,得∴(舍去),故该运动员的成绩为.
21.解:(1)∵ 反比例函数y=的图象经过点A(2,3),
∴ m=6.∴ 反比例函数的解析式是y=.
∵ 点B(-3,n)在反比例函数y=的图象上,
∴ n=-2.∴ B(-3,-2).
∵ 一次函数y=kx+b的图象经过A(2,3)、B(-3,-2)两点,
∴ 解得
∴ 一次函数的解析式是y=x+1.
(2)OP的长为3或1.
22.解:(1)将点C坐标(,2)代入,得,所以;
将点C坐标(,2)代入,得,所以.
(2)联立方程组解得或
所以点D坐标为(-2,1).
(3)当>时,一次函数图象在反比例函数图象上方,
此时x的取值范围是.
23.解: (1)将点(3,2)代入,
得,解得.
所以函数关系式为.
(2)图象如图所示,其顶点坐标为.
( http: / / www.21cnjy.com )
(3)当时,由,解得.
当时,由图象可知当时,.所以的取值范围是.
24.解:(1)y=700-20(x-45)=-20x+1 600.
(2)P=(x-40)(-20x+1 600)=-20+2 400x-64 000=-20+8 000.
∵ x≥45,a=-20<0,∴ 当x=60时,=8 000(元).
即当每盒售价定为60元时,每天销售的利润最大,最大利润为8 000元.
(3)由题意,得-20+8 000=6 000,
解这个方程,得=50,=70.
∵ 抛物线P=-20+8 000的开口向下,
∴ 当50≤x≤70时,每天销售粽子的利润不低于6 000元.
又∵ x≤58,∴ 50≤x≤58.
∵ 在y=-20x+1 600中,k=-20<0,
∴ y随x的增大而减小.
∴ 当x=58时,=-20×58+1 600=440.
即超市每天至少销售粽子440盒.
25.解:(1)由题意知,点在抛物线上,
所以解得,
所以抛物线的函数关系式是(0≤x≤12).
答:该抛物线的函数关系式为(0≤x≤12),拱顶D到地面OA的距离为10 m.
(2)由题意知,当车最外侧与地面OA的交点为(2,0)(或(10,0)),
当时,,所以可以通过.
(3)令,即,
可得,解得.
所以.
答:两排灯的水平距离最小是 m.
x
y
O
第2题图
第3题图
第19题图
B
(本检测题满分:100分,时间:90分钟)
一、选择题(每小题3分,共30分)
1.如果反比例函数y的图象经过点,则k的值是( )
A.2 B. C D.3
2.已知二次函数的图象如图所示,则对应a,k的符号正确的是( )
A. B.
C. D.
3.(2014·重庆中考)如图,反比例函数在第二象限的图象上有两点A、B,它们的横坐标分别为-1、-3,直线AB与x轴交于点C,则△AOC的面积为( )
A.8 B.10 C.12 D.24
4.(2012·兰州中考)在反比例函数y (k<0)的图象上有两点( 1,y1),(,y2),则y1 y2的值是( )
A.负数 B.非正数 C.正数 D.不能确定
5.(2015·安徽中考)如图,一次函数y1= x与二次函数y2=ax2+bx+c的图象相交于P,Q两点,则函数y =ax2+(b1)x+c的图象可能为( )
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
第5题图 A B C D
6. (2015·天津中考)已知抛物线y=-+x+6与x轴交于点A,点B,与y轴交于点C,若D为AB的中点,则CD的长为( )
A. B. C. D.
7. 如图,A为反比例函数图象上一点,AB垂直轴于点B,若S△AOB=3,则的值为 ( )
A.6 B.3
C. D.不能确定
8.已知M、N两点关于y轴对称,且点M在双曲线y 上,点N在直线y x 3上,设点M的坐标为(a,b),则二次函数y abx2 (a b)x( )
A.有最大值,最大值为B.有最大值,最大值为
C.有最小值,最小值为 D.有最小值,最小值为
9.(2015·湖北孝感中考)如图 ,二次函数yax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:
①abc<0;②0;③ac-b+10;④OA·OB=.
其中正确结论的个数是( )
( http: / / www.21cnjy.com )
第9题图
A.4 B.3 C.2 D.1
10.在函数(a为常数)的图象上有三点( 3,y1),( 1,y2),(2,y3),则函数值y1,y2,y3的大小关系是( )
A. B.
C. D.
二、填空题(每小题3分,共24分)
11.点P在反比例函数y (k≠0)的图象上,点Q(2,4)与点P关于y轴对称,则此反比例函数的关系式为 .
12. 将抛物线向右平移2个单位后,再向下平移5个单位,所得抛物线的顶点坐标为_______.
13.试写出图象位于第二、四象限的一个反比例函数的关系式 .
14.若反比例函数的图象位于第一、三象限,正比例函数的图象过第二、四象限,则的整数值是________.
15.抛物线在轴上截得的线段长度是 .
16.设三点依次分别是抛物线与轴的交点以及与轴的两个交点,则△的面积是 .
17.把二次函数y (x-1)2 2的图象绕原点旋转180°后得到的图象的关系式为 .
18.若M(2,2)和N(b, 1 n2)是反比例函数y 图象上的两点,则一次函数y kx b的图象经过第 象限.
三、解答题(共46分)
19.(6分)(2014·北京中考)在平面直角坐标系中,抛物线经过点A(0, -2),B(3, 4).
(1)求抛物线的表达式及对称轴;
(2)设点B关于原点的对称点为C,点D是 ( http: / / www.21cnjy.com )抛物线对称轴上一动点,记抛物线在A,B之间的部分为图象G(包含A, B两点).若直线CD与图象G有公共点,结合函数图象,求点D纵坐标t的取值范围.
20.(6分)如图所示,一个运动员推铅球,铅球在点A处出手,出手时球离地面约.铅球落地点在B处,铅球运行中在运动员前4 m处(即 m)达到最高点,最高点高3 m.已知铅球经过的路线是抛物线,根据图示的直角坐标系,你能算出该运动员的成绩吗
21.(6分)(2015·贵州安顺中考)如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=的图象交于A(2,3)、B(-3,n)两点.
( http: / / www.21cnjy.com )
第21题图
(1)求一次函数和反比例函数的解析式;
(2)若P是y轴上一点,且满足△PAB的面积是5,直接写出OP的长.
22.(7分)如图,已知直线与轴、轴分别交于点A、B,与反比例函数 ()的图象分别交于点C、D,且点C的坐标为(,2).
(1)分别求出直线AB及反比例函数的关 系式;
(2)求出点D的坐标;
(3)利用图象直接写出:当x在什么范围内取值时,>.
23.(7分)已知函数的图象经过点(3,2).
(1)求这个函数的关系式;
(2)画出它的图象,并指出图象的顶点坐标;
(3)当时,求使得的的取值范围.
24.(7分)(2015 湖北襄阳中考)为 ( http: / / www.21cnjy.com )满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌粽子,每盒进价是40元,超市规定每盒售价不得少于45元.根据以往销售经验发现:当售价定为每盒45元时,每天可卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;
(2)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?
(3)为稳定物价,有关管理部门限定:这种粽 ( http: / / www.21cnjy.com )子的每盒售价不得高于58元.如果超市想要每天获得不低于6 000元的利润,那么超市每天至少销售粽子多少盒?
25.(7分)(2015·山东青岛中考)如图,隧道的截面由抛物线和长方形构成,长方形的长是12 m,宽是4 m.按照图中所示的直角坐标系,抛物线可以用表示,且抛物线上的点C到墙面OB的水平距离为3 m,到地面OA的距离为m.
(1)求该抛物线的函数关系式,并计算出拱顶D到地面OA的距离.
(2)一辆货运汽车载一长方体集装箱后高为6 m,宽为4 m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8 m,那么两排灯的水平距离最小是多少米?
( http: / / www.21cnjy.com )
第25题图
第21章 二次函数与反比例函数检测题参考答案
一、选择题
1.D 解析:把代入得-2=,∴ k 3.
2. D 解析:二次函数的图象开口向上时开口向下时图象交于y 轴正半轴时交于y轴负半轴时
3.C 解析: ∵ 点A、B都在反比例函数的图象上,∴ A(-1,6),B(-3,2).设直线AB的表达式为,则解得
∴ 直线AB的表达式为,∴ C(-4,0).在△中,OC=4,OC边上的高(即点A到x轴的距离)为6,∴ △的面积在平面直角坐标系中求三角形的面积时,一般要将落在坐标轴上的一边作为底.
4. A 解析:由题意知y1 k,y2 4k.∵ k<0,∴ y1-y2 -k-(-4k) 3k<0.
5.A 解析:一次函数 ( http: / / www.21cnjy.com )y1=x与二次函数y2=ax2+bx+c的图象有两个交点,且都在第一象限,可知一元二次方程ax2+bx+c=x,即ax2+(b-1)x+c=0有两个不相等的正实数根,所以函数y=ax2+(b-1)x+c的图象与x轴的正半轴有两个不同的交点,故选项A符合题意.
6. D 解析:令y=0,即-+x+6=0,解得=-3,=12,所以A、B两点的坐标为(-3,0)、(12,0),所以点D的横坐标为x==,所以OD=(O为坐标原点).因为抛物线与y轴交于点C,所以点C的坐标为(0,6),所以OC=6.在Rt△COD中,CD===.故选D.
7.A 解析:设A点的坐标为,则OB a,AB ,则
则k 6.
8.B 解析:∵ 点M的坐标为(a,b),∴ 点N的坐标为(-a,b).
∵ 点M在双曲线y 上,∴ ab .
∵ 点N(-a,b)在直线y x 3上,∴ -a 3 b.∴ a b 3.
∴ 二次函数y -abx2 (a b)x x2 3x (x-3)2 .
∴ 二次函数y -abx2 (a b)x有最大值,最大值为.
9.B 解析:因为抛物线开口向下,与y轴交于正半轴,对称轴x>0,且与x轴有两个交点,所以a<0,b>0,c>0,>0,所以abc<0,<0,故①正确,②错误.
因为OA=OC,所以点A的坐标可表示为(-c,0),代入解析式得,所以,故③正确.
设点A、B的坐标分别为(),(),所以是方程的两根,所以.又OA=-,OB=,所以,故④正确.所以①③④正确.
10. D 解析:是反比例函数,且,
∴ 双曲线的图象在第二、四象限,在各个象限内,y随x的增大而增大.
和在第二象限,且,∴ 0<y1<y2.
又∵ 点(2,y3)在第四象限,∴ y3<0.
因此y1,y2,y3的大小关系是y3<y1<y2.
二、填空题
11.y 解析:设点P(x,y),∵ 点P与点Q(2,4)关于y轴对称,则P,4),
∴ kxy2×4 -8.∴ y .
12.
13. 答案不唯一,如 解析:设反比例函数的关系式为y ,∵ 反比例函数的图象位于第二、四象限,∴ k 0,据此写出一个函数关系式即可,如k -1,则.
14.4 解析:由反比例函数的图象位于第一、三象限,得,即.又正比例函数的图象过第二、四象限,所以,所以.所以的整数值是4.
15.4 解析:由得,所以抛物线在轴上截得的线段长度是.
16. 解析:令,令,得,
所以,
所以△的面积是.
17.y -(x 1)2-2 解析:抛物线绕原点旋转180°后,开口方向与原抛物线开口方向相反,开口大小不变,顶点坐标变为),
∴ 旋转180°后得到的函数图象的关系式为y -(x 1)2-2.
18.一、三、四 解析:把M(2,2)代入y 得2 ,解得k 4.
把N(b,-1-n2)代入y 得-1-n2 ,即﹣(1 n2) ,∴ b<0,
∴ y kx b中,k 4>0,b<0,∴ 图象经过第一、三、四象限.
三、解答题
19.解:(1)∵ 经过点A(0,-2),B(3,4),
代入得∴
∴ 抛物线的表达式为
∴ 其对称轴为直线x=-1.
(2)由题意可知C(-3,-4),二次函数的最小值为-4.
( http: / / www.21cnjy.com )
第19题答图
由图象可以看出D点纵坐标最小值即为-4,
最大值即BC与对称轴交点的纵坐标.
设直线BC的函数表达式为y=kx b,
根据题意得解得
∴ 直线BC的函数表达式为
当x=1时,
∴ 点D纵坐标t的取值范围是
20.解:能.∵ OC=4 m,CD=3 m,,∴ 顶点的坐标为(4,3).
设 3,
把代入上式,得 ,∴,
∴ 即.
令,得∴(舍去),故该运动员的成绩为.
21.解:(1)∵ 反比例函数y=的图象经过点A(2,3),
∴ m=6.∴ 反比例函数的解析式是y=.
∵ 点B(-3,n)在反比例函数y=的图象上,
∴ n=-2.∴ B(-3,-2).
∵ 一次函数y=kx+b的图象经过A(2,3)、B(-3,-2)两点,
∴ 解得
∴ 一次函数的解析式是y=x+1.
(2)OP的长为3或1.
22.解:(1)将点C坐标(,2)代入,得,所以;
将点C坐标(,2)代入,得,所以.
(2)联立方程组解得或
所以点D坐标为(-2,1).
(3)当>时,一次函数图象在反比例函数图象上方,
此时x的取值范围是.
23.解: (1)将点(3,2)代入,
得,解得.
所以函数关系式为.
(2)图象如图所示,其顶点坐标为.
( http: / / www.21cnjy.com )
(3)当时,由,解得.
当时,由图象可知当时,.所以的取值范围是.
24.解:(1)y=700-20(x-45)=-20x+1 600.
(2)P=(x-40)(-20x+1 600)=-20+2 400x-64 000=-20+8 000.
∵ x≥45,a=-20<0,∴ 当x=60时,=8 000(元).
即当每盒售价定为60元时,每天销售的利润最大,最大利润为8 000元.
(3)由题意,得-20+8 000=6 000,
解这个方程,得=50,=70.
∵ 抛物线P=-20+8 000的开口向下,
∴ 当50≤x≤70时,每天销售粽子的利润不低于6 000元.
又∵ x≤58,∴ 50≤x≤58.
∵ 在y=-20x+1 600中,k=-20<0,
∴ y随x的增大而减小.
∴ 当x=58时,=-20×58+1 600=440.
即超市每天至少销售粽子440盒.
25.解:(1)由题意知,点在抛物线上,
所以解得,
所以抛物线的函数关系式是(0≤x≤12).
答:该抛物线的函数关系式为(0≤x≤12),拱顶D到地面OA的距离为10 m.
(2)由题意知,当车最外侧与地面OA的交点为(2,0)(或(10,0)),
当时,,所以可以通过.
(3)令,即,
可得,解得.
所以.
答:两排灯的水平距离最小是 m.
x
y
O
第2题图
第3题图
第19题图
B
