辽宁省铁岭市实验学校九年级数学下册 7.3 特殊角的三角函数
文档属性
| 名称 | 辽宁省铁岭市实验学校九年级数学下册 7.3 特殊角的三角函数 |
|
|
| 格式 | zip | ||
| 文件大小 | 35.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-01 09:51:52 | ||
图片预览

文档简介
7.3 特殊角三角函数值
学习目标
1、能推导并熟记30°、45°、60°角的三角函数值,并能根据这些值说出对应锐角度数;
2、能熟练计算含有30°、45°、60°角的三角函数的运算式;
3、渗透数形结合的数学思想,培养学生良好的学习习惯.
教学重点
熟记30°、45°、60°角的三角函数值,能熟练计算含有30°、45°、60°角的三角函数的运算式。
教学难点
30°、45°、60°角的三角函数值的推导过程。
一、知识回顾
一个直角三角形中,一个锐角正弦是怎么定义的?
一个锐角余弦是怎么定义的?
一个锐角正切是怎么定义的?
二、 探索活动
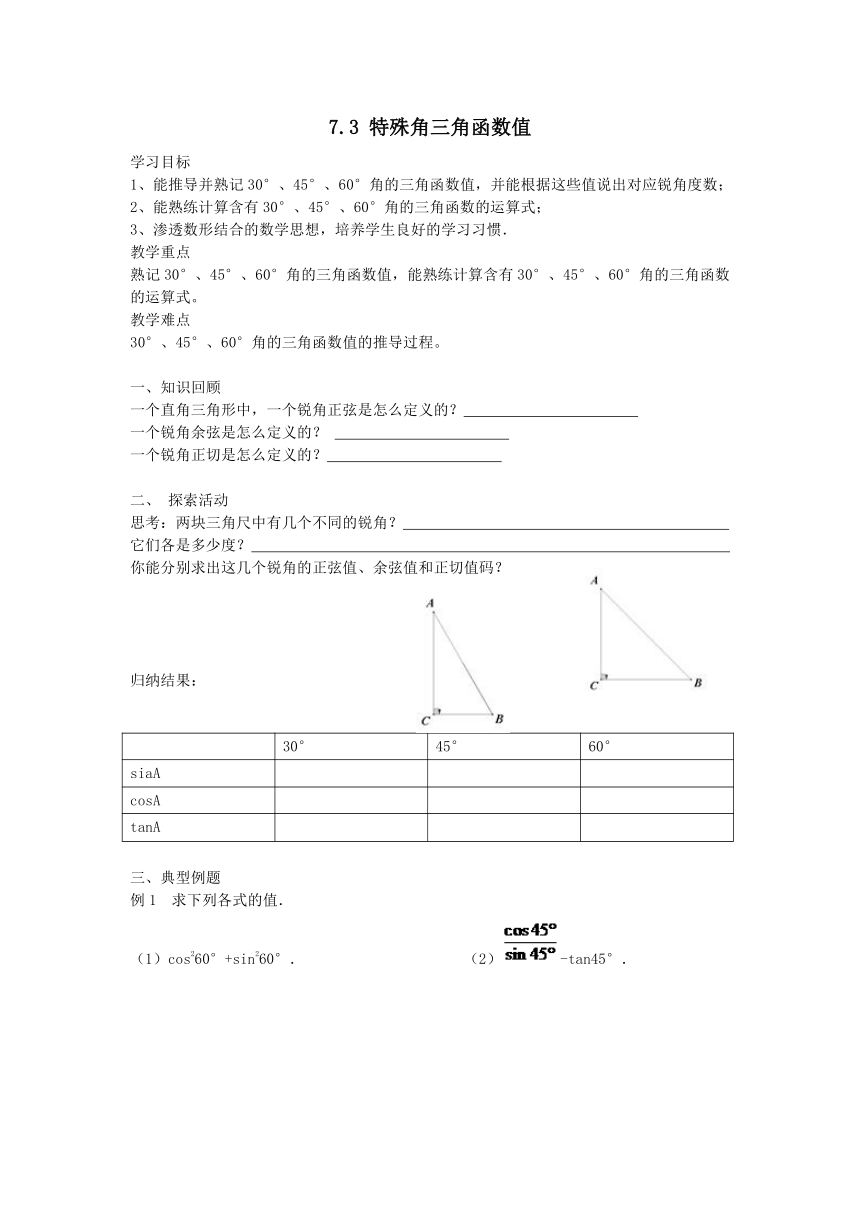
思考:两块三角尺中有几个不同的锐角?
它们各是多少度?
你能分别求出这几个锐角的正弦值、余弦值和正切值码?
归纳结果:
30° 45° 60°
siaA
cosA
tanA
三、典型例题
例1 求下列各式的值.
(1)cos260°+sin260°. (2)-tan45°.
例2 (1)如图(1),在Rt△ABC中,∠C=90,AB=,BC=,求∠A的度数.
(2)如图(2),已知圆锥的高AO等于圆锥的底面半径OB的倍,是AB与OB的夹角,求.
四、 巩固反馈
1.已知:Rt△ABC中,∠C=90°,cosA=,AB=15,则AC的长是( ).
A.3 B.6 C.9 D.12
2.下列各式中不正确的是( ).
A.sin260°+cos260°=1 B.sin30°+cos30°=1
C.sin35°=cos55° D.tan45°>sin45°
3.计算2sin30°-2cos60°+tan45°的结果是( ).
A.2 B. C. D.1
4.已知∠A为锐角,且cosA≤,那么( )
A.0°<∠A≤60°B.60°≤∠A<90°C.0°<∠A≤30°D.30°≤∠A<90°
5.在△ABC中,∠A、∠B都是锐角,且sinA=,cosB=,则△ABC的形状是( )
A.直角三角形 B.钝角三角形C.锐角三角形 D.不能确定
6.如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D,BC=3,AC=4,设∠BCD=a,则tanA的值为( ).
A. B. C. D.
7.当锐角a>60°时,cosa的值( ).
A.小于 B.大于 C.大于 D.大于1
8.在△ABC中,三边之比为a:b:c=1:: 2,则sinA+tanA等于( ).
A.
9.已知梯形ABCD中,腰BC长为2,梯形对角线BD垂直平分AC,若梯形的高是,则∠CAB等于( )
A.30° B.60° C.45° D.以上都不对
10.sin272°+sin218°的值是( ).
A.1 B.0 C. D.
学习目标
1、能推导并熟记30°、45°、60°角的三角函数值,并能根据这些值说出对应锐角度数;
2、能熟练计算含有30°、45°、60°角的三角函数的运算式;
3、渗透数形结合的数学思想,培养学生良好的学习习惯.
教学重点
熟记30°、45°、60°角的三角函数值,能熟练计算含有30°、45°、60°角的三角函数的运算式。
教学难点
30°、45°、60°角的三角函数值的推导过程。
一、知识回顾
一个直角三角形中,一个锐角正弦是怎么定义的?
一个锐角余弦是怎么定义的?
一个锐角正切是怎么定义的?
二、 探索活动
思考:两块三角尺中有几个不同的锐角?
它们各是多少度?
你能分别求出这几个锐角的正弦值、余弦值和正切值码?
归纳结果:
30° 45° 60°
siaA
cosA
tanA
三、典型例题
例1 求下列各式的值.
(1)cos260°+sin260°. (2)-tan45°.
例2 (1)如图(1),在Rt△ABC中,∠C=90,AB=,BC=,求∠A的度数.
(2)如图(2),已知圆锥的高AO等于圆锥的底面半径OB的倍,是AB与OB的夹角,求.
四、 巩固反馈
1.已知:Rt△ABC中,∠C=90°,cosA=,AB=15,则AC的长是( ).
A.3 B.6 C.9 D.12
2.下列各式中不正确的是( ).
A.sin260°+cos260°=1 B.sin30°+cos30°=1
C.sin35°=cos55° D.tan45°>sin45°
3.计算2sin30°-2cos60°+tan45°的结果是( ).
A.2 B. C. D.1
4.已知∠A为锐角,且cosA≤,那么( )
A.0°<∠A≤60°B.60°≤∠A<90°C.0°<∠A≤30°D.30°≤∠A<90°
5.在△ABC中,∠A、∠B都是锐角,且sinA=,cosB=,则△ABC的形状是( )
A.直角三角形 B.钝角三角形C.锐角三角形 D.不能确定
6.如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D,BC=3,AC=4,设∠BCD=a,则tanA的值为( ).
A. B. C. D.
7.当锐角a>60°时,cosa的值( ).
A.小于 B.大于 C.大于 D.大于1
8.在△ABC中,三边之比为a:b:c=1:: 2,则sinA+tanA等于( ).
A.
9.已知梯形ABCD中,腰BC长为2,梯形对角线BD垂直平分AC,若梯形的高是,则∠CAB等于( )
A.30° B.60° C.45° D.以上都不对
10.sin272°+sin218°的值是( ).
A.1 B.0 C. D.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
