云南省下关重点中学2023-2024学年高一下学期开学考试数学试题(含解析)
文档属性
| 名称 | 云南省下关重点中学2023-2024学年高一下学期开学考试数学试题(含解析) | 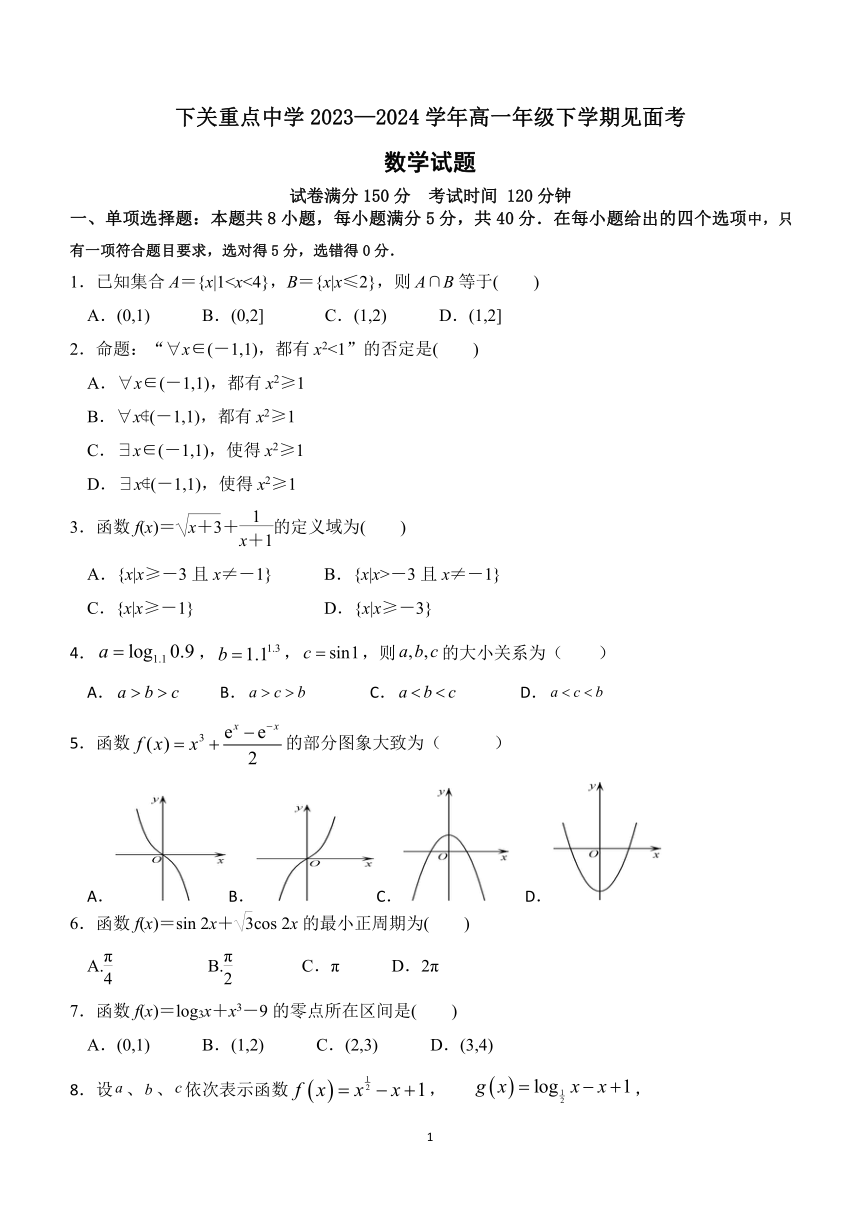 | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-10 10:41:57 | ||
图片预览





文档简介
下关重点中学2023—2024学年高一年级下学期见面考
数学试题
试卷满分150分 考试时间 120分钟
一、单项选择题:本题共8小题,每小题满分5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求,选对得5分,选错得0分.
1.已知集合A={x|1A.(0,1) B.(0,2] C.(1,2) D.(1,2]
2.命题:“ x∈(-1,1),都有x2<1”的否定是( )
A. x∈(-1,1),都有x2≥1
B. x (-1,1),都有x2≥1
C. x∈(-1,1),使得x2≥1
D. x (-1,1),使得x2≥1
3.函数f(x)=+的定义域为( )
A.{x|x≥-3且x≠-1} B.{x|x>-3且x≠-1}
C.{x|x≥-1} D.{x|x≥-3}
4.,,,则的大小关系为( )
A. B. C. D.
5.函数的部分图象大致为( )
A.B.C. D.
6.函数f(x)=sin 2x+cos 2x的最小正周期为( )
A. B. C.π D.2π
7.函数f(x)=log3x+x3-9的零点所在区间是( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
8.设、、依次表示函数, ,
的零点,则、、的大小关系为( ).
A. B. C. D.
多项选择题:本题共4小题,每小题满分5分,共20分. 在每小题给出的四个选项中,有多项符合题目要求。全部选对得5分,部分选对得2分,有选错的得0分.
9.下列结论正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
10.下列各式中,值为的是( )
A. B.
C. D.
11.将函数的图象向左平移个单位长度,得到函数的图象,则函数具有以下哪些性质( )
A.最大值为,图象关于直线对称 B.图象关于y轴对称
C.最小正周期为 D.图象关于点成中心对称
12.设函数,若,且,则的值可以是( )
A.4 B.5 C. D.6
填空题:本题共4小题,每小题5分,共20分。
13.log24+log42=________.
14.设x>0,y>0,x+y=4,则+的最小值为________.
15.已知,则__________.
16.设函数在区间上的最大值为M,最小值为N,则 的值为______.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分10分)
已知集合,集合.
(1)若是的必要不充分条件,求实数的取值范围;
(2)若,求实数的取值范围.
18.(本小题满分12分)
已知函数.
(1)求函数的对称中心;
(2)当时,求函数的值域.
19.(本小题满分12分)
在中,内角、、的对边分别为、、,已知.
(1)求的值;
(2)若,,求的面积.
20.(本小题满分12分)
某手机生产商计划在2023年利用新技术生产某款新手机,通过市场分析,生产此款手机全年需投入固定成本200万元,每生产(千部)手机,需另投人成本万元,且,由市场调研知,每部手机售价0.5万元,且全年内生产的手机当年能全部销售完.
(1)求出2023年的利润(万元)关于年产量(千部)的函数关系式;(利润销售额成本)
(2)2023年产量为多少千部时,该生产商所获利润最大 最大利润是多少
(本小题满分12分)
已知函数,,.
(1)若,使得方程有解,求实数的取值范围;
(2)若对任意的,总存在,使得,求实数的取值范围;
(3)设,记为函数在上的最大值,求的最小值.
22.(本小题满分12分)
已知函数的最小正周期为,其图象关于点对称.
(1)令,判断函数的奇偶性;
(2)是否存在实数满足对任意,任意,使成立.若存在,求的取值范围;若不存在,说明理由.
参考答案
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的选项中,只有一项是符合题目要求的)
题号 1 2 3 4 5 6 7 8
答案 D C A D B C C D
【解析】
1.答案 D解析 ∵A={x|12.答案 C解析 命题是全称量词命题,则否定是存在量词命题,即 x∈(-1,1),使得x2≥1.
3.答案 A解析 要使f(x)有意义,则解得x≥-3,且x≠-1,
∴f(x)的定义域为{x|x≥-3,且x≠-1}.
4.答案 D解析 ,,因为,函数在区间内单调递增,所以,所以.
5.答案 B解析 的定义域为,,所以是奇函数,由此排除CD选项.,排除A选项. 选B
6.答案 C解析 ∵f(x)=sin 2x+cos 2x=2sin,∴最小正周期T==π.
7.答案 C解析 ∵f(2)=log32-1<0,f(3)=log33+27-9=19>0,∴f(2)·f(3)<0,∴函数在区间(2,3)上存在零点.
8.答案 D解析依题意可得,的图象与的图象交点的横坐标为,
作出图象如图:
由图象可知,
二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项是符合题目要求的.全部选对的得5分,部分选对的得2分,有选错的得0分)
题号 9 10 11 12
答案 BC AD BCD AB
9.【答案】BC【解】对于A:当时,若取,则有.故A不正确;
对于B:当时,两边同乘以,有,即.故B正确;
对于C:当,两边同乘以,则.故C正确;
对于D:当时,取,有.故D不正确.
10.【答案】AD 【解】对于A:,故A正确;
对于D:,故D正确.
11.【答案】BCD 【解】由题意,,
对A:的最大值为,最小值为,因为,所以函数的图象不关于直线对称,故选项A错误;
对B:因为,所以函数为偶函数,其图象关于y轴对称,故选项B正确;
对C:由周期公式有,所以函数的最小正周期为,故选项C正确;
对D:因为,所以函数的图象关于点成中心对称,故选项D正确.故选:BCD.
12.【答案】AB【解】函数的图象如图所示,设,由图可知,
当时,直线与函数的图象有四个交点,
交点的横坐标分别为,,,,且,时,
令,解得或.由图可知,,,,
由,可得,则有,
所以.
令,易知在上为减函数,且,,
故,且,,故选AB.
三、填空题(本大题共4小题,每小题5分,共20分)
题号 13 14 15 16
答案 1
13.答案 解析 根据题干得到log24+log42=2+=2+=.
14. 答案 解析 ∵x+y=4,∴+=(x+y)=,又x>0,y>0,
则+≥2=4,则+≥×(5+4)=.
答案 解析 因为,由,解得,所以 . 故答案为:
16.答案 1 解析 由题意知,(),设,则,
因为,所以为奇函数,所以在区间上的最大值与最小值的和为0, 故,所以.
四、解答题.(本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。)
17.(本小题满分10分)
【解】(1)∵是的必要不充分条件,∴是的真子集.①当B= 时,2a-1>a+1 a>2
②B≠ 时,∴,解得.∴实数的取值范围为 (2,+∞).
由,①当B= 时,2a-1>a+1 a>2
②B≠ 时,可得或,解得或.
∴实数的取值范围为(-∞,-3]∪(1,+∞).
18.(本小题满分12分)
【解】(1)由题意,函数,
令,解得,所以函数的对称中心为.
(2))因为,可得,当时,即时,可得;
当时,即时,可得,所以函数的值域为.
19.(本小题满分12分)
【解】(1),
,
,
,,;
(2)由(1)可得,由余弦定理可得,
,解得,则,,,
.
20.(本小题满分12分)
【解】(1)销售千部手机获得的销售额为:
当时,;
当时,
故,
(2)当时,,
当时,,
当时,,
当且仅当,即时,等号成立, 因为,
所以当 (千部)时,所获利润最大,最大利润为:3800万元.
21.(本小题满分12分)
【解】(1),,
因为函数的图象的对称轴是直线,
所以在上为减函数,,,
故,所以的取值范围为.
(2)对任意的,总存在,使得,
在区间上,,
函数图象的对称轴是直线,
又,当时,函数有最大值为,
①当时,,不符合题意,舍去;
②当时,在上的值域为,,得;
③当时,在上的值域为,,得,
综上,的取值范围为.
(3)函数为的对称轴为,
①当或时,在[0,1]上单调递增,则;
②当时,,
解不等式组得,
故当,综上,
在上单调递减,在上单调递增,
时取最小值为.
22.(本小题满分12分)
【解】(1)的最小正周期为.函数的图象关于点对称,
.,
,易得定义域为,
函数为偶函数.
(2)由(1)可知,实数满足对任意,任意,
使得成立
即成立
令,设,
那么
,
可等价转化为:在上恒成立.
令,其图象对称轴,
①当时,即,解得;
②当,即时,,解得;
③当,即时,,解得;
综上可得,存在,且的取值范围是.
数学试题
试卷满分150分 考试时间 120分钟
一、单项选择题:本题共8小题,每小题满分5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求,选对得5分,选错得0分.
1.已知集合A={x|1
2.命题:“ x∈(-1,1),都有x2<1”的否定是( )
A. x∈(-1,1),都有x2≥1
B. x (-1,1),都有x2≥1
C. x∈(-1,1),使得x2≥1
D. x (-1,1),使得x2≥1
3.函数f(x)=+的定义域为( )
A.{x|x≥-3且x≠-1} B.{x|x>-3且x≠-1}
C.{x|x≥-1} D.{x|x≥-3}
4.,,,则的大小关系为( )
A. B. C. D.
5.函数的部分图象大致为( )
A.B.C. D.
6.函数f(x)=sin 2x+cos 2x的最小正周期为( )
A. B. C.π D.2π
7.函数f(x)=log3x+x3-9的零点所在区间是( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
8.设、、依次表示函数, ,
的零点,则、、的大小关系为( ).
A. B. C. D.
多项选择题:本题共4小题,每小题满分5分,共20分. 在每小题给出的四个选项中,有多项符合题目要求。全部选对得5分,部分选对得2分,有选错的得0分.
9.下列结论正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
10.下列各式中,值为的是( )
A. B.
C. D.
11.将函数的图象向左平移个单位长度,得到函数的图象,则函数具有以下哪些性质( )
A.最大值为,图象关于直线对称 B.图象关于y轴对称
C.最小正周期为 D.图象关于点成中心对称
12.设函数,若,且,则的值可以是( )
A.4 B.5 C. D.6
填空题:本题共4小题,每小题5分,共20分。
13.log24+log42=________.
14.设x>0,y>0,x+y=4,则+的最小值为________.
15.已知,则__________.
16.设函数在区间上的最大值为M,最小值为N,则 的值为______.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分10分)
已知集合,集合.
(1)若是的必要不充分条件,求实数的取值范围;
(2)若,求实数的取值范围.
18.(本小题满分12分)
已知函数.
(1)求函数的对称中心;
(2)当时,求函数的值域.
19.(本小题满分12分)
在中,内角、、的对边分别为、、,已知.
(1)求的值;
(2)若,,求的面积.
20.(本小题满分12分)
某手机生产商计划在2023年利用新技术生产某款新手机,通过市场分析,生产此款手机全年需投入固定成本200万元,每生产(千部)手机,需另投人成本万元,且,由市场调研知,每部手机售价0.5万元,且全年内生产的手机当年能全部销售完.
(1)求出2023年的利润(万元)关于年产量(千部)的函数关系式;(利润销售额成本)
(2)2023年产量为多少千部时,该生产商所获利润最大 最大利润是多少
(本小题满分12分)
已知函数,,.
(1)若,使得方程有解,求实数的取值范围;
(2)若对任意的,总存在,使得,求实数的取值范围;
(3)设,记为函数在上的最大值,求的最小值.
22.(本小题满分12分)
已知函数的最小正周期为,其图象关于点对称.
(1)令,判断函数的奇偶性;
(2)是否存在实数满足对任意,任意,使成立.若存在,求的取值范围;若不存在,说明理由.
参考答案
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的选项中,只有一项是符合题目要求的)
题号 1 2 3 4 5 6 7 8
答案 D C A D B C C D
【解析】
1.答案 D解析 ∵A={x|1
3.答案 A解析 要使f(x)有意义,则解得x≥-3,且x≠-1,
∴f(x)的定义域为{x|x≥-3,且x≠-1}.
4.答案 D解析 ,,因为,函数在区间内单调递增,所以,所以.
5.答案 B解析 的定义域为,,所以是奇函数,由此排除CD选项.,排除A选项. 选B
6.答案 C解析 ∵f(x)=sin 2x+cos 2x=2sin,∴最小正周期T==π.
7.答案 C解析 ∵f(2)=log32-1<0,f(3)=log33+27-9=19>0,∴f(2)·f(3)<0,∴函数在区间(2,3)上存在零点.
8.答案 D解析依题意可得,的图象与的图象交点的横坐标为,
作出图象如图:
由图象可知,
二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项是符合题目要求的.全部选对的得5分,部分选对的得2分,有选错的得0分)
题号 9 10 11 12
答案 BC AD BCD AB
9.【答案】BC【解】对于A:当时,若取,则有.故A不正确;
对于B:当时,两边同乘以,有,即.故B正确;
对于C:当,两边同乘以,则.故C正确;
对于D:当时,取,有.故D不正确.
10.【答案】AD 【解】对于A:,故A正确;
对于D:,故D正确.
11.【答案】BCD 【解】由题意,,
对A:的最大值为,最小值为,因为,所以函数的图象不关于直线对称,故选项A错误;
对B:因为,所以函数为偶函数,其图象关于y轴对称,故选项B正确;
对C:由周期公式有,所以函数的最小正周期为,故选项C正确;
对D:因为,所以函数的图象关于点成中心对称,故选项D正确.故选:BCD.
12.【答案】AB【解】函数的图象如图所示,设,由图可知,
当时,直线与函数的图象有四个交点,
交点的横坐标分别为,,,,且,时,
令,解得或.由图可知,,,,
由,可得,则有,
所以.
令,易知在上为减函数,且,,
故,且,,故选AB.
三、填空题(本大题共4小题,每小题5分,共20分)
题号 13 14 15 16
答案 1
13.答案 解析 根据题干得到log24+log42=2+=2+=.
14. 答案 解析 ∵x+y=4,∴+=(x+y)=,又x>0,y>0,
则+≥2=4,则+≥×(5+4)=.
答案 解析 因为,由,解得,所以 . 故答案为:
16.答案 1 解析 由题意知,(),设,则,
因为,所以为奇函数,所以在区间上的最大值与最小值的和为0, 故,所以.
四、解答题.(本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。)
17.(本小题满分10分)
【解】(1)∵是的必要不充分条件,∴是的真子集.①当B= 时,2a-1>a+1 a>2
②B≠ 时,∴,解得.∴实数的取值范围为 (2,+∞).
由,①当B= 时,2a-1>a+1 a>2
②B≠ 时,可得或,解得或.
∴实数的取值范围为(-∞,-3]∪(1,+∞).
18.(本小题满分12分)
【解】(1)由题意,函数,
令,解得,所以函数的对称中心为.
(2))因为,可得,当时,即时,可得;
当时,即时,可得,所以函数的值域为.
19.(本小题满分12分)
【解】(1),
,
,
,,;
(2)由(1)可得,由余弦定理可得,
,解得,则,,,
.
20.(本小题满分12分)
【解】(1)销售千部手机获得的销售额为:
当时,;
当时,
故,
(2)当时,,
当时,,
当时,,
当且仅当,即时,等号成立, 因为,
所以当 (千部)时,所获利润最大,最大利润为:3800万元.
21.(本小题满分12分)
【解】(1),,
因为函数的图象的对称轴是直线,
所以在上为减函数,,,
故,所以的取值范围为.
(2)对任意的,总存在,使得,
在区间上,,
函数图象的对称轴是直线,
又,当时,函数有最大值为,
①当时,,不符合题意,舍去;
②当时,在上的值域为,,得;
③当时,在上的值域为,,得,
综上,的取值范围为.
(3)函数为的对称轴为,
①当或时,在[0,1]上单调递增,则;
②当时,,
解不等式组得,
故当,综上,
在上单调递减,在上单调递增,
时取最小值为.
22.(本小题满分12分)
【解】(1)的最小正周期为.函数的图象关于点对称,
.,
,易得定义域为,
函数为偶函数.
(2)由(1)可知,实数满足对任意,任意,
使得成立
即成立
令,设,
那么
,
可等价转化为:在上恒成立.
令,其图象对称轴,
①当时,即,解得;
②当,即时,,解得;
③当,即时,,解得;
综上可得,存在,且的取值范围是.
同课章节目录
