人教版八年级数学上册《13.3 等边三角形》同步练习
文档属性
| 名称 | 人教版八年级数学上册《13.3 等边三角形》同步练习 |
|
|
| 格式 | zip | ||
| 文件大小 | 210.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-01 16:12:39 | ||
图片预览



文档简介
等边三角形
典题探究
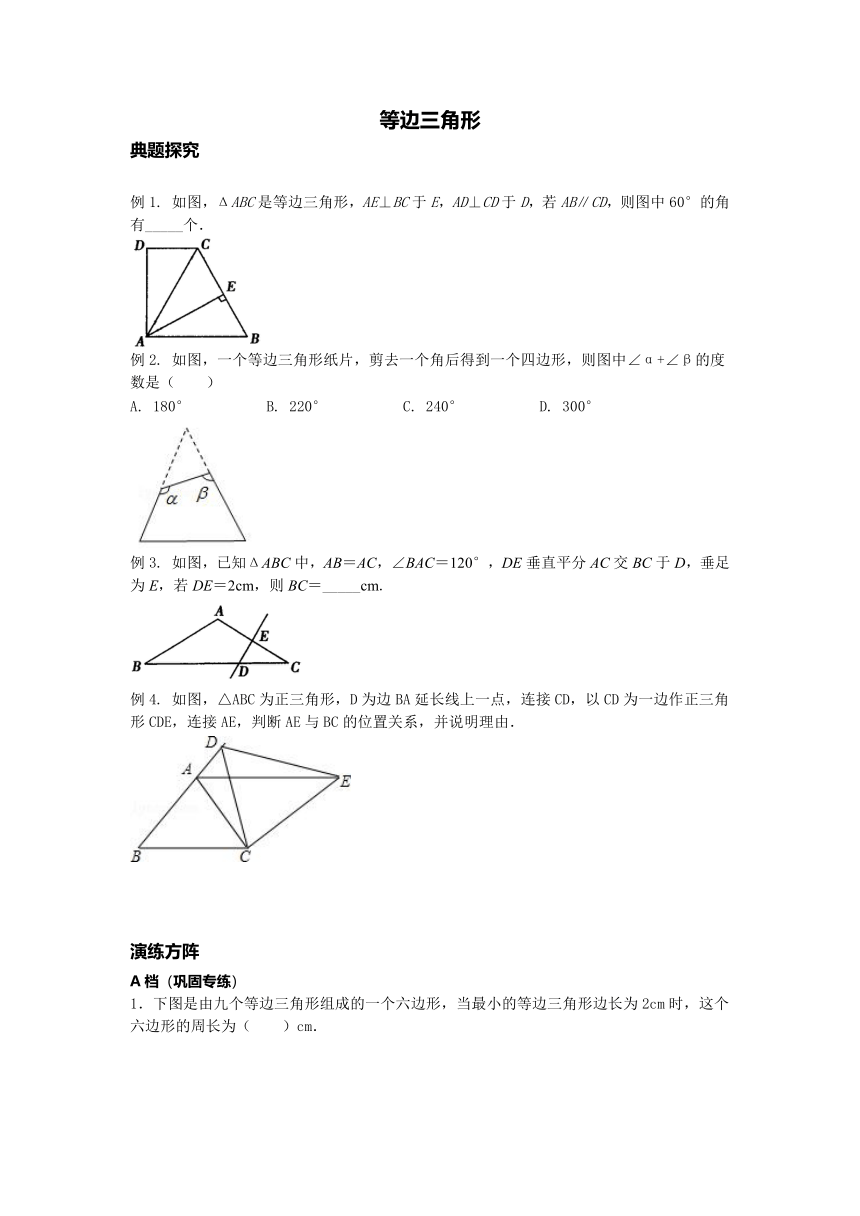
例1. 如图,ΔABC是等边三角形,AE⊥BC于E,AD⊥CD于D,若AB∥CD,则图中60°的角有_____个.
( http: / / www.21cnjy.com )
例2. 如图,一个等边三角形纸片,剪去一个角后得到一个四边形,则图中∠α+∠β的度数是( )
A. 180° B. 220° C. 240° D. 300°
( http: / / www.21cnjy.com )
例3. 如图,已知ΔABC中,AB=AC ( http: / / www.21cnjy.com ),∠BAC=120°,DE垂直平分AC交BC于D,垂足为E,若DE=2cm,则BC=_____cm.
( http: / / www.21cnjy.com )
例4. 如图,△ABC为正三角形,D为边B ( http: / / www.21cnjy.com )A延长线上一点,连接CD,以CD为一边作正三角形CDE,连接AE,判断AE与BC的位置关系,并说明理由.
( http: / / www.21cnjy.com )
演练方阵
A档(巩固专练)
1.下图是由九个等边三角形组成的一个六边形,当最小的等边三角形边长为2cm时,这个六边形的周长为( )cm.
( http: / / www.21cnjy.com )
A. 30 B. 40 C. 50 D. 60
2.如图,△ABC中,AB=AC,△DEF为等边三角形,则α、β、γ之间的关系为( )
( http: / / www.21cnjy.com )
A. B. C. D.
3.如图,等边△ABC的边长为4,AD是B ( http: / / www.21cnjy.com )C边上的中线,F是AD边上的动点,E是AC边上一点,若AE=2,当EF+CF取得最小值时,则∠ECF的度数为( )
( http: / / www.21cnjy.com )
A. 15° B. 22.5° C. 30° D. 45°
4.如图,△ABC是等边三 ( http: / / www.21cnjy.com )角形,P是BC上任意一点,PD⊥AB,PE⊥AC,连接DE.记△ADE的周长为L1,四边形BDEC的周长为L2,则L1与L2的大小关系是( )
( http: / / www.21cnjy.com )
A. Ll=L2 B. L1>L2 C. L2>L1 D. 无法确定
5.如图,△ABC为边长是5的等边三角形,点E在AC边上,点F在AB边上,ED⊥BC,且ED=AE,DF=AF,则CE的长是( )
( http: / / www.21cnjy.com )
A. B. C. 20+10 D. 20﹣10
6.如图中左边图形,连接等边三角形的各 ( http: / / www.21cnjy.com )边中点将得到一个小等边三角形,右边的图形就是这样得到的,请问右边图形中的阴影部分面积大还是空白部分面积大( )
( http: / / www.21cnjy.com )
A. 阴影部分面积大 B. 空白部分面积大 C.一样大 D. 不确定
7.如图,等边三角形ABC内有一点 ( http: / / www.21cnjy.com )P,过点P向三边作垂线,垂足分别为S、Q、R,且PQ=6,PR=8,PS=10,则△ABC的面积等于( )
( http: / / www.21cnjy.com )
A. 190 B. 192 C. 194 D. 196
8.在边长为2cm的等边三角形内,随意取一些点,如果要保证所取的点中一定存在距离小于1cm的两点,那么取的点至少应有( )
A. 4个 B. 5个 C. 6个 D. 7个
9.如图,已知等边△ABC外有一点 ( http: / / www.21cnjy.com )P,P落在∠ABC内,设点P到BC、CA、AB三边的距离分别为h1、h2、h3,且满足h2+h3﹣h1=6,那么等边△ABC的面积为( )
( http: / / www.21cnjy.com )
A. 12 B. 9 C. 8 D. 4
10.如图所示,△ABC为正三角形,P是BC上的一点,PM⊥AB,PN⊥AC,设四边形AMPN,△ABC的周长分别为m、n,则有( )
( http: / / www.21cnjy.com )
A. B. C. D.
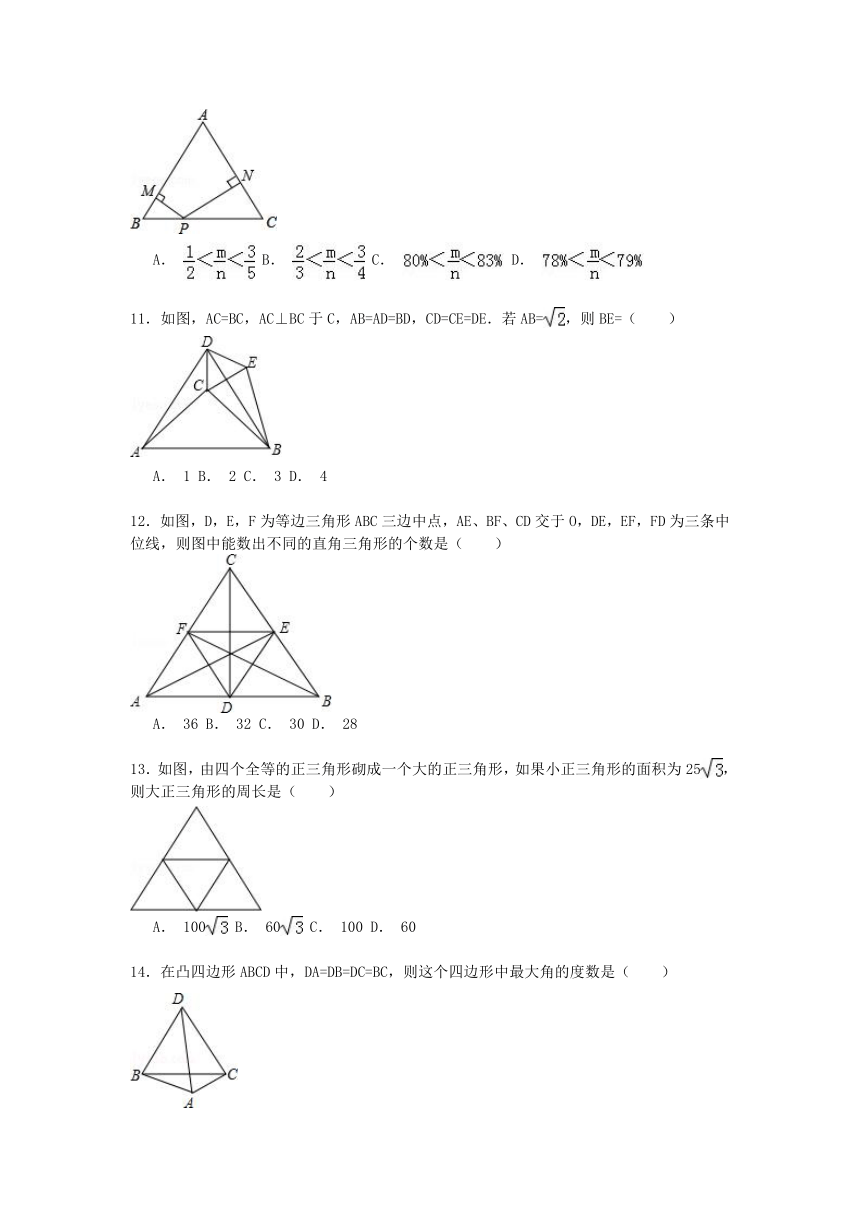
11.如图,AC=BC,AC⊥BC于C,AB=AD=BD,CD=CE=DE.若AB=,则BE=( )
( http: / / www.21cnjy.com )
A. 1 B. 2 C. 3 D. 4
12.如图,D,E,F为等边三角形ABC三边 ( http: / / www.21cnjy.com )中点,AE、BF、CD交于O,DE,EF,FD为三条中位线,则图中能数出不同的直角三角形的个数是( )
( http: / / www.21cnjy.com )
A. 36 B. 32 C. 30 D. 28
13.如图,由四个全等的正三角形砌成一个大的正三角形,如果小正三角形的面积为25,则大正三角形的周长是( )
( http: / / www.21cnjy.com )
A. 100 B. 60 C. 100 D. 60
14.在凸四边形ABCD中,DA=DB=DC=BC,则这个四边形中最大角的度数是( )
( http: / / www.21cnjy.com )
A. 120° B. 135° C. 150° D. 165°
B档(提升精练)
15.如图,△ABC是边长 ( http: / / www.21cnjy.com )为3的等边三角形,△BDC是等腰三角形,且∠BDC=120°.以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,则△AMN的周长为 _________ .
( http: / / www.21cnjy.com )
16.如图,将边长为3+的等边△ABC折叠,折痕为DE,点B与点F重合,EF和DF分别交AC于点M、N,DF⊥AB,垂足为D,AD=1,则重叠部分的面积为 _________ .
( http: / / www.21cnjy.com )
17.如右图,以等边△O ( http: / / www.21cnjy.com )AB的高OC为边向逆时针方向作等边△OCD,CD交OB于点E,再以OE为边向逆时针方向作等边△OEF,EF交OD于点G,再以OG为边向逆时针方向作等边△OGH,…,按此方法操作,最终得到△OMN,此时ON在OA上.若AB=1,则ON= _________ .
( http: / / www.21cnjy.com )
18.已知正△ABC的面积是1,P是△ ( http: / / www.21cnjy.com )ABC内一点,并且△PAB、△PBC、△PCA的面积相等,那么满足条件的点P共有 _________ 个;△PAB的面积是 _________ .
19.如图,从等边三角形内一点向三边作垂线,已知这三条垂线段的长分别为1、3、5,则这个等边三角形的边长为 _________ .
( http: / / www.21cnjy.com )
20.如图所示,直线AB、CD相交于点O.若OM=ON=MN,那么∠APQ+∠CQP= _________ .
( http: / / www.21cnjy.com )
21.在正△ABC中(如图),D为AC ( http: / / www.21cnjy.com )上一点,E为AB上一点,BD,CE相交于P,若四边形ADPE与△BPC的面积相等,那么∠BPE= _________ .
( http: / / www.21cnjy.com )
22.如图,平行于BC的线段MN把 ( http: / / www.21cnjy.com )等边△ABC分成一个三角形和一个四边形,已知△AMN和四边形MBCN的周长相等,则BC与MN的长度之比是 _________ .
( http: / / www.21cnjy.com )
23.正三角形ABC的边长BC=2,以该等边三角形的高AD为正方形的边长,则正方形的面积为 _________ .
C档(跨越导练)
24.阅读材料:
如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r1,r2,腰上的高为h,连接AP,则S△ABP+S△ACP=S△ABC,即:,∴r1+r2=h(定值).
(1)类比与推理
如果把“等腰三角形”改成“等边三角形”, ( http: / / www.21cnjy.com )那么P的位置可以由“在底边上任一点”放宽为“在三角形内任一点”,即:已知等边△ABC内任意一点P到各边的距离分别为r1,r2,r3,等边△ABC的高为h,试证明r1+r2+r3=h(定值).
(2)理解与应用
△ABC中,∠C=90°,AB=10,AC=8,BC=6,△ABC内部是否存在一点O,点O到各边的距离相等? _________ (填“存在”或“不存在”),若存在,请直接写出这个距离r的值,r= _________ .若不存在,请说明理由. ( http: / / www.21cnjy.com )
25.小明在找等边三角形ABC一边的 ( http: / / www.21cnjy.com )三等分点时,他是这样做的,先做∠ABC、∠ACB的角平分线并且相交于点O,然后做线段BO、CO的垂直平分线,分别交BC于E、F,他说:“E、F就是BC边的三等分点.”你同意他的说法吗?请说明你的理由.
( http: / / www.21cnjy.com )
26.在等边△ABC中,D是AC的中点,E是BC延长线上一点,且CE=CD,
(1)请说明DB=DE的理由.
(2)若等边△ABC的边长为4cm,求△BDE的面积.
( http: / / www.21cnjy.com )
27.如图,设O为△ABC内一点,且∠ ( http: / / www.21cnjy.com )AOB=∠BOC=∠COA=120°,P为任意一点(不是O).求证:PA+PB+PC>OA+OB+OC.
( http: / / www.21cnjy.com )
28.如图,等边△ABC,D、E分别在BC、AC上,且CD=AE,AD、BE相交于点P,试求∠BPD的度数.
( http: / / www.21cnjy.com )
29.阅读下列材料,解答相应问题:
已知△ABC是等边三角形,AD ( http: / / www.21cnjy.com )是高,设AD=h.点P(不与点A、B、C重合)到AB的距离PE=h1,到AC的距离PF=h2,到BC的距离PH=h3.
如图1,当点P与点D重合时,我们容易发现:h1=h,h2=h,因此得到:h1+h2=h.
小明同学大胆猜想提出问题:如图2,若点P在BC边上,但不与点D重合,结论h1+h2=h还成立吗?通过证明,他得到了肯定的答案.证明如下:
证明:如图3,连接AP.
∴S△ABC=S△ABP+S△APC.
设等边三角形的边长AB=BC=CA=a.
∵AD⊥BC,PE⊥AB,PF⊥AC,
∴BC AD=AB PE+AC PF
∴a h=a h1+a h2.
∴h1+h2=h.
(1)进一步猜想:当点P在BC的延长线 ( http: / / www.21cnjy.com )上,上述结论还成立吗?若成立,请你证明;若不成立,请猜想h1,h2与 h之间的数量关系,并证明.(借助答题卡上的图4)
(2)我们容易知道,当点P在CB的延长线及直线AB,AC上时,情况与前述类似,这里不再说明.
继续猜想,你会进一步提出怎样的问题呢?请在答题卡上借助图5画出示意图,写出你提出的问题,并直接写出结论,不必证明.
( http: / / www.21cnjy.com )
30.如图△ABC是边长为2的等边三角形, ( http: / / www.21cnjy.com )D是AB边的中点,P是BC边上的动点,Q是AC边上的动点,当P、Q的位置在何处时,才能使△DPQ的周长最小?并求出这个最值.
( http: / / www.21cnjy.com )
典题探究
例1. 如图,ΔABC是等边三角形,AE⊥BC于E,AD⊥CD于D,若AB∥CD,则图中60°的角有_____个.
( http: / / www.21cnjy.com )
例2. 如图,一个等边三角形纸片,剪去一个角后得到一个四边形,则图中∠α+∠β的度数是( )
A. 180° B. 220° C. 240° D. 300°
( http: / / www.21cnjy.com )
例3. 如图,已知ΔABC中,AB=AC ( http: / / www.21cnjy.com ),∠BAC=120°,DE垂直平分AC交BC于D,垂足为E,若DE=2cm,则BC=_____cm.
( http: / / www.21cnjy.com )
例4. 如图,△ABC为正三角形,D为边B ( http: / / www.21cnjy.com )A延长线上一点,连接CD,以CD为一边作正三角形CDE,连接AE,判断AE与BC的位置关系,并说明理由.
( http: / / www.21cnjy.com )
演练方阵
A档(巩固专练)
1.下图是由九个等边三角形组成的一个六边形,当最小的等边三角形边长为2cm时,这个六边形的周长为( )cm.
( http: / / www.21cnjy.com )
A. 30 B. 40 C. 50 D. 60
2.如图,△ABC中,AB=AC,△DEF为等边三角形,则α、β、γ之间的关系为( )
( http: / / www.21cnjy.com )
A. B. C. D.
3.如图,等边△ABC的边长为4,AD是B ( http: / / www.21cnjy.com )C边上的中线,F是AD边上的动点,E是AC边上一点,若AE=2,当EF+CF取得最小值时,则∠ECF的度数为( )
( http: / / www.21cnjy.com )
A. 15° B. 22.5° C. 30° D. 45°
4.如图,△ABC是等边三 ( http: / / www.21cnjy.com )角形,P是BC上任意一点,PD⊥AB,PE⊥AC,连接DE.记△ADE的周长为L1,四边形BDEC的周长为L2,则L1与L2的大小关系是( )
( http: / / www.21cnjy.com )
A. Ll=L2 B. L1>L2 C. L2>L1 D. 无法确定
5.如图,△ABC为边长是5的等边三角形,点E在AC边上,点F在AB边上,ED⊥BC,且ED=AE,DF=AF,则CE的长是( )
( http: / / www.21cnjy.com )
A. B. C. 20+10 D. 20﹣10
6.如图中左边图形,连接等边三角形的各 ( http: / / www.21cnjy.com )边中点将得到一个小等边三角形,右边的图形就是这样得到的,请问右边图形中的阴影部分面积大还是空白部分面积大( )
( http: / / www.21cnjy.com )
A. 阴影部分面积大 B. 空白部分面积大 C.一样大 D. 不确定
7.如图,等边三角形ABC内有一点 ( http: / / www.21cnjy.com )P,过点P向三边作垂线,垂足分别为S、Q、R,且PQ=6,PR=8,PS=10,则△ABC的面积等于( )
( http: / / www.21cnjy.com )
A. 190 B. 192 C. 194 D. 196
8.在边长为2cm的等边三角形内,随意取一些点,如果要保证所取的点中一定存在距离小于1cm的两点,那么取的点至少应有( )
A. 4个 B. 5个 C. 6个 D. 7个
9.如图,已知等边△ABC外有一点 ( http: / / www.21cnjy.com )P,P落在∠ABC内,设点P到BC、CA、AB三边的距离分别为h1、h2、h3,且满足h2+h3﹣h1=6,那么等边△ABC的面积为( )
( http: / / www.21cnjy.com )
A. 12 B. 9 C. 8 D. 4
10.如图所示,△ABC为正三角形,P是BC上的一点,PM⊥AB,PN⊥AC,设四边形AMPN,△ABC的周长分别为m、n,则有( )
( http: / / www.21cnjy.com )
A. B. C. D.
11.如图,AC=BC,AC⊥BC于C,AB=AD=BD,CD=CE=DE.若AB=,则BE=( )
( http: / / www.21cnjy.com )
A. 1 B. 2 C. 3 D. 4
12.如图,D,E,F为等边三角形ABC三边 ( http: / / www.21cnjy.com )中点,AE、BF、CD交于O,DE,EF,FD为三条中位线,则图中能数出不同的直角三角形的个数是( )
( http: / / www.21cnjy.com )
A. 36 B. 32 C. 30 D. 28
13.如图,由四个全等的正三角形砌成一个大的正三角形,如果小正三角形的面积为25,则大正三角形的周长是( )
( http: / / www.21cnjy.com )
A. 100 B. 60 C. 100 D. 60
14.在凸四边形ABCD中,DA=DB=DC=BC,则这个四边形中最大角的度数是( )
( http: / / www.21cnjy.com )
A. 120° B. 135° C. 150° D. 165°
B档(提升精练)
15.如图,△ABC是边长 ( http: / / www.21cnjy.com )为3的等边三角形,△BDC是等腰三角形,且∠BDC=120°.以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,则△AMN的周长为 _________ .
( http: / / www.21cnjy.com )
16.如图,将边长为3+的等边△ABC折叠,折痕为DE,点B与点F重合,EF和DF分别交AC于点M、N,DF⊥AB,垂足为D,AD=1,则重叠部分的面积为 _________ .
( http: / / www.21cnjy.com )
17.如右图,以等边△O ( http: / / www.21cnjy.com )AB的高OC为边向逆时针方向作等边△OCD,CD交OB于点E,再以OE为边向逆时针方向作等边△OEF,EF交OD于点G,再以OG为边向逆时针方向作等边△OGH,…,按此方法操作,最终得到△OMN,此时ON在OA上.若AB=1,则ON= _________ .
( http: / / www.21cnjy.com )
18.已知正△ABC的面积是1,P是△ ( http: / / www.21cnjy.com )ABC内一点,并且△PAB、△PBC、△PCA的面积相等,那么满足条件的点P共有 _________ 个;△PAB的面积是 _________ .
19.如图,从等边三角形内一点向三边作垂线,已知这三条垂线段的长分别为1、3、5,则这个等边三角形的边长为 _________ .
( http: / / www.21cnjy.com )
20.如图所示,直线AB、CD相交于点O.若OM=ON=MN,那么∠APQ+∠CQP= _________ .
( http: / / www.21cnjy.com )
21.在正△ABC中(如图),D为AC ( http: / / www.21cnjy.com )上一点,E为AB上一点,BD,CE相交于P,若四边形ADPE与△BPC的面积相等,那么∠BPE= _________ .
( http: / / www.21cnjy.com )
22.如图,平行于BC的线段MN把 ( http: / / www.21cnjy.com )等边△ABC分成一个三角形和一个四边形,已知△AMN和四边形MBCN的周长相等,则BC与MN的长度之比是 _________ .
( http: / / www.21cnjy.com )
23.正三角形ABC的边长BC=2,以该等边三角形的高AD为正方形的边长,则正方形的面积为 _________ .
C档(跨越导练)
24.阅读材料:
如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r1,r2,腰上的高为h,连接AP,则S△ABP+S△ACP=S△ABC,即:,∴r1+r2=h(定值).
(1)类比与推理
如果把“等腰三角形”改成“等边三角形”, ( http: / / www.21cnjy.com )那么P的位置可以由“在底边上任一点”放宽为“在三角形内任一点”,即:已知等边△ABC内任意一点P到各边的距离分别为r1,r2,r3,等边△ABC的高为h,试证明r1+r2+r3=h(定值).
(2)理解与应用
△ABC中,∠C=90°,AB=10,AC=8,BC=6,△ABC内部是否存在一点O,点O到各边的距离相等? _________ (填“存在”或“不存在”),若存在,请直接写出这个距离r的值,r= _________ .若不存在,请说明理由. ( http: / / www.21cnjy.com )
25.小明在找等边三角形ABC一边的 ( http: / / www.21cnjy.com )三等分点时,他是这样做的,先做∠ABC、∠ACB的角平分线并且相交于点O,然后做线段BO、CO的垂直平分线,分别交BC于E、F,他说:“E、F就是BC边的三等分点.”你同意他的说法吗?请说明你的理由.
( http: / / www.21cnjy.com )
26.在等边△ABC中,D是AC的中点,E是BC延长线上一点,且CE=CD,
(1)请说明DB=DE的理由.
(2)若等边△ABC的边长为4cm,求△BDE的面积.
( http: / / www.21cnjy.com )
27.如图,设O为△ABC内一点,且∠ ( http: / / www.21cnjy.com )AOB=∠BOC=∠COA=120°,P为任意一点(不是O).求证:PA+PB+PC>OA+OB+OC.
( http: / / www.21cnjy.com )
28.如图,等边△ABC,D、E分别在BC、AC上,且CD=AE,AD、BE相交于点P,试求∠BPD的度数.
( http: / / www.21cnjy.com )
29.阅读下列材料,解答相应问题:
已知△ABC是等边三角形,AD ( http: / / www.21cnjy.com )是高,设AD=h.点P(不与点A、B、C重合)到AB的距离PE=h1,到AC的距离PF=h2,到BC的距离PH=h3.
如图1,当点P与点D重合时,我们容易发现:h1=h,h2=h,因此得到:h1+h2=h.
小明同学大胆猜想提出问题:如图2,若点P在BC边上,但不与点D重合,结论h1+h2=h还成立吗?通过证明,他得到了肯定的答案.证明如下:
证明:如图3,连接AP.
∴S△ABC=S△ABP+S△APC.
设等边三角形的边长AB=BC=CA=a.
∵AD⊥BC,PE⊥AB,PF⊥AC,
∴BC AD=AB PE+AC PF
∴a h=a h1+a h2.
∴h1+h2=h.
(1)进一步猜想:当点P在BC的延长线 ( http: / / www.21cnjy.com )上,上述结论还成立吗?若成立,请你证明;若不成立,请猜想h1,h2与 h之间的数量关系,并证明.(借助答题卡上的图4)
(2)我们容易知道,当点P在CB的延长线及直线AB,AC上时,情况与前述类似,这里不再说明.
继续猜想,你会进一步提出怎样的问题呢?请在答题卡上借助图5画出示意图,写出你提出的问题,并直接写出结论,不必证明.
( http: / / www.21cnjy.com )
30.如图△ABC是边长为2的等边三角形, ( http: / / www.21cnjy.com )D是AB边的中点,P是BC边上的动点,Q是AC边上的动点,当P、Q的位置在何处时,才能使△DPQ的周长最小?并求出这个最值.
( http: / / www.21cnjy.com )
