山东省夏津第六中学八年级数学下册17.1折叠---勾股定理应用(共21张PPT)
文档属性
| 名称 | 山东省夏津第六中学八年级数学下册17.1折叠---勾股定理应用(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 964.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-01 00:00:00 | ||
图片预览



文档简介
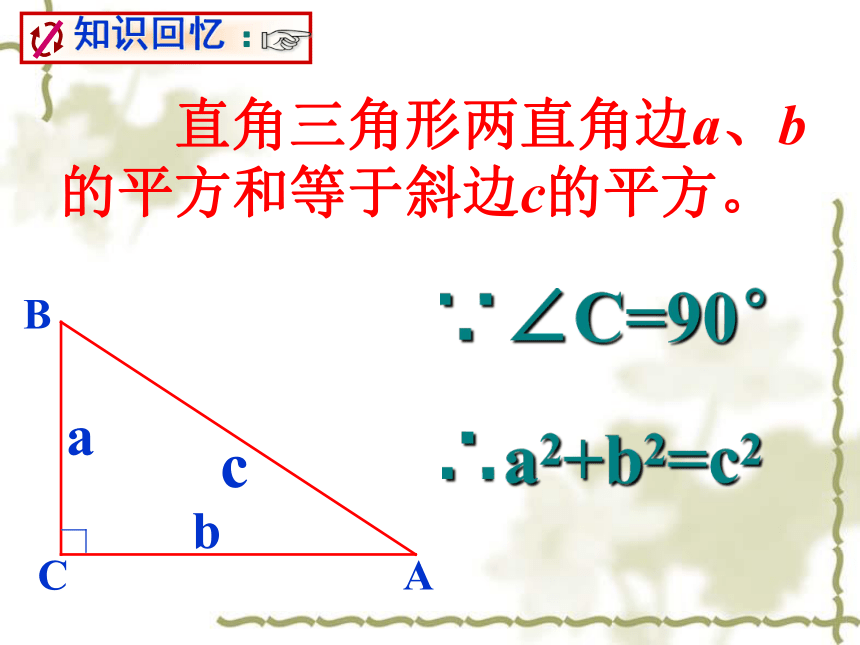
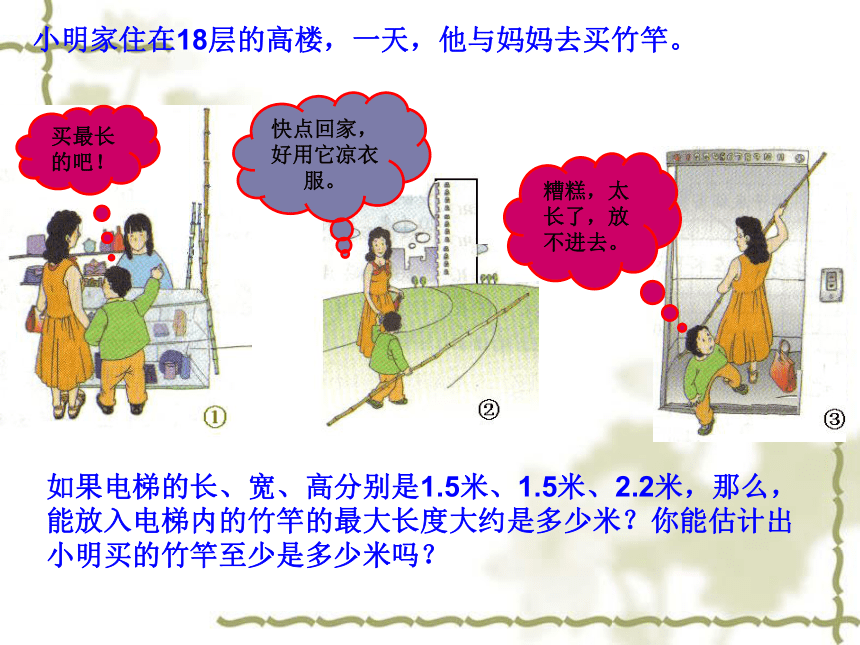
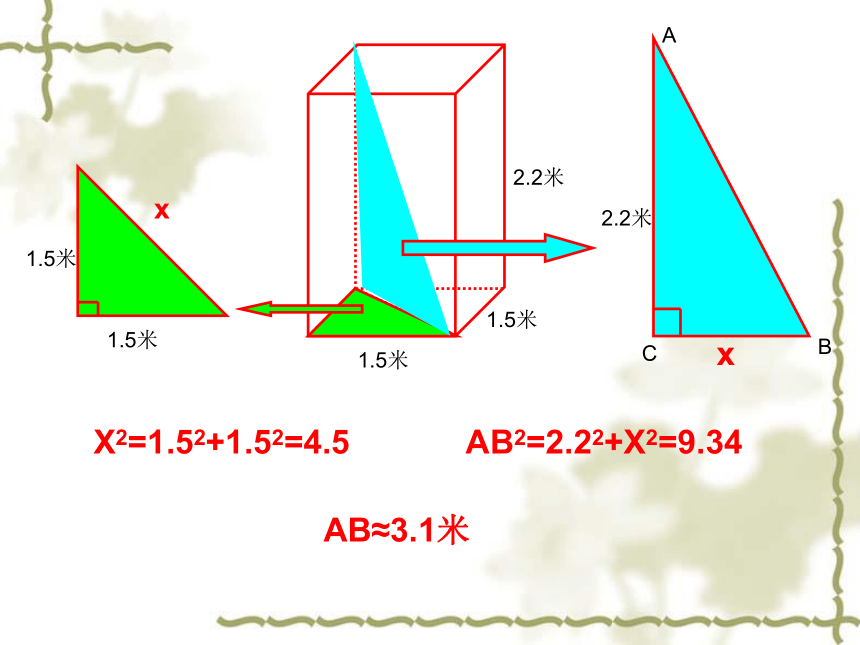
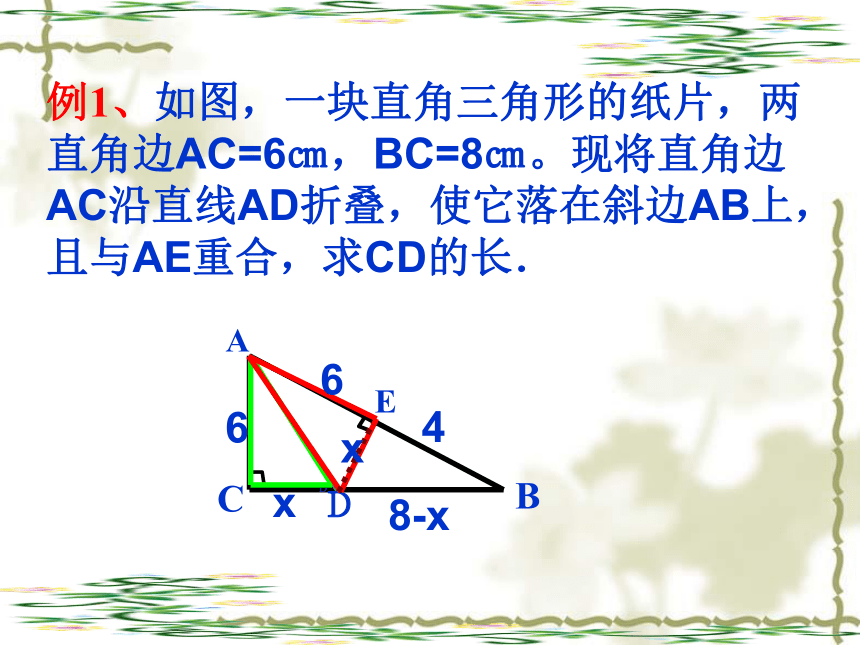
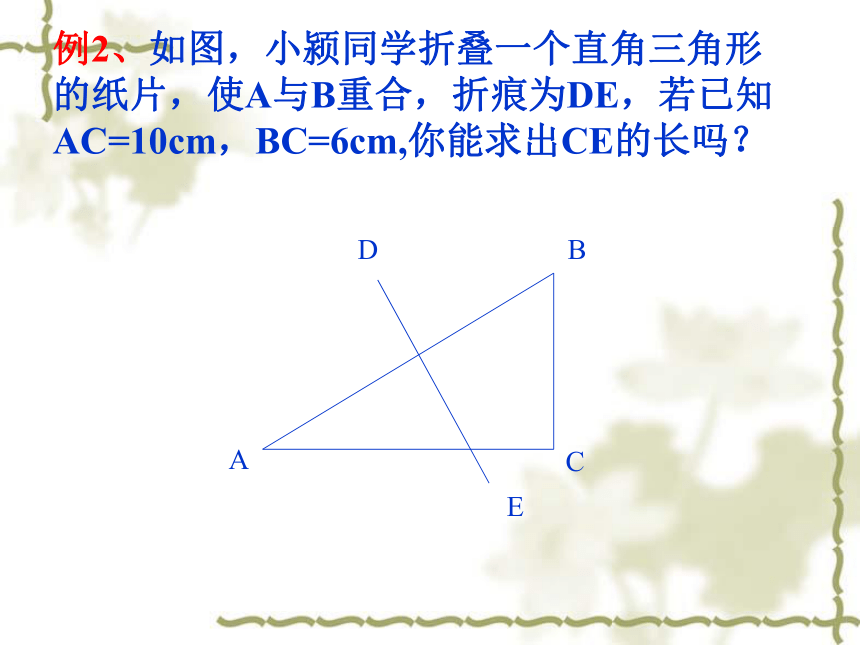
课件21张PPT。勾股定理应用 直角三角形两直角边a、b的平方和等于斜边c的平方。CAB∵∠C=90°∴a2+b2=c2生活中的勾股定理小明家住在18层的高楼,一天,他与妈妈去买竹竿。买最长的吧!快点回家,好用它凉衣服。糟糕,太长了,放不进去。如果电梯的长、宽、高分别是1.5米、1.5米、2.2米,那么,能放入电梯内的竹竿的最大长度大约是多少米?你能估计出小明买的竹竿至少是多少米吗?xX2=1.52+1.52=4.5AB2=2.22+X2=9.34AB≈3.1米折叠三角形例1、如图,一块直角三角形的纸片,两直角边AC=6㎝,BC=8㎝。现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长. ACDBE第8题图Dx6x8-x46例2、如图,小颍同学折叠一个直角三角形
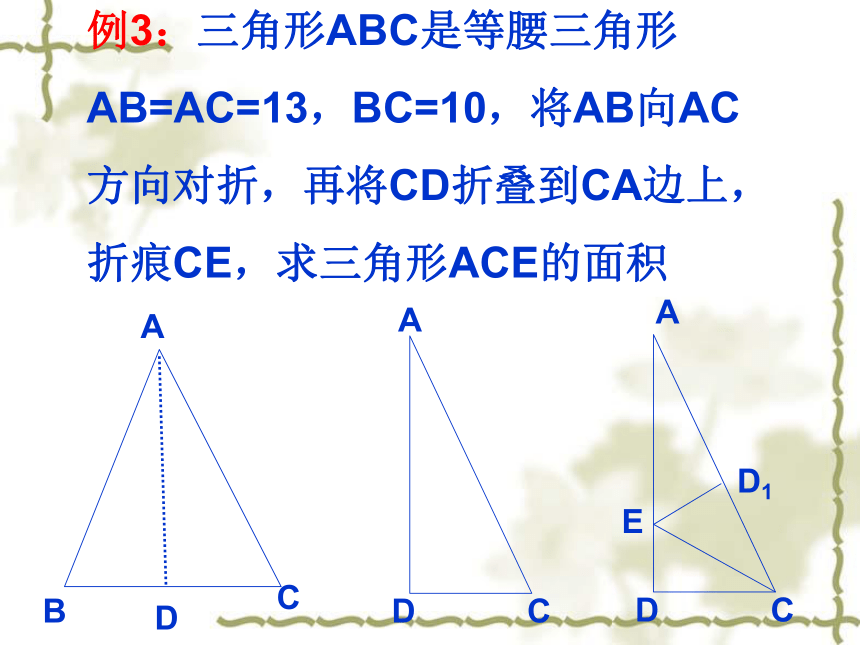
的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?C例3:三角形ABC是等腰三角形
AB=AC=13,BC=10,将AB向AC
方向对折,再将CD折叠到CA边上,
折痕CE,求三角形ACE的面积ABCDADCDAD1E折叠四边形例2:折叠矩形纸片,先折出折痕对角线BD,在绕点D折叠,使点A落在BD的E处,折痕DG,若AB=2,BC=1,求AG的长。DAGBCE例1:折叠矩形ABCD的一边AD,点D落在BC边上的点F处,已知AB=8CM,BC=10CM,求 1.CF 2.EC.ABCDEF810106X8-X48-X例3:矩形ABCD中,AB=6,BC=8,先把它对折,折痕为EF,展开后再沿BG折叠,使A落在EF上的A1,求第二次折痕BG的长。ABCDEFA1G提示:先证明正三角形AA1B例2:矩形ABCD如图折叠,使点D落在BC边上的点F处,已知AB=8,BC=10,求折痕AE的长。ABCDFE立体图形展开问题杜登尼(Dudeney,1857-1930年)是19世纪英国知名的谜题创作者.“蜘蛛和苍蝇”问题最早出现在1903年的英国报纸上,它是杜登尼最有名的谜题之一.它对全世界难题爱好者的挑战,长达四分之三个世纪.想挑战世纪谜题吗?立体图平面图化归ACB C C4m如图,有一棱长为4m的立方体房间,一只蜘蛛在A处. 最短
路程⑵若苍蝇在C处,则最短路程是多少? 4m4m⑴若一只苍蝇在B处,蜘蛛去抓苍蝇需要爬行的最短路程是多少? 变式四:如图,一圆柱体木块的底面周长为24cm,高AB为4cm ,BC是直径,一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程大约是( )
A.6cm B.12cm C.13cm D.16cm沿AB剪开策略迁移 ∵ 底面圆的周长为24cm ∴BB1=24cm
又∵点C 是BB1 的中点 ∴BC=12cm
而∵AB=4cm ∴ 在Rt△ABC中,根据勾股定理得: AC2=AB2+BC2 cm
∴选C
?
?
如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程( 取3)是( )
A.20cm B.10cm C.14cm D.无法确定 BB8OA2蛋糕ACB8周长的一半
6圆柱(锥)中的最值问题如图是一个三级台阶,它的每一级的长宽和高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,
A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿
着台阶面爬到B点最短路程是多少?
20232323ABC∵ AB2=AC2+BC2=625,
∴ AB=25.台阶中的最值问题
的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?C例3:三角形ABC是等腰三角形
AB=AC=13,BC=10,将AB向AC
方向对折,再将CD折叠到CA边上,
折痕CE,求三角形ACE的面积ABCDADCDAD1E折叠四边形例2:折叠矩形纸片,先折出折痕对角线BD,在绕点D折叠,使点A落在BD的E处,折痕DG,若AB=2,BC=1,求AG的长。DAGBCE例1:折叠矩形ABCD的一边AD,点D落在BC边上的点F处,已知AB=8CM,BC=10CM,求 1.CF 2.EC.ABCDEF810106X8-X48-X例3:矩形ABCD中,AB=6,BC=8,先把它对折,折痕为EF,展开后再沿BG折叠,使A落在EF上的A1,求第二次折痕BG的长。ABCDEFA1G提示:先证明正三角形AA1B例2:矩形ABCD如图折叠,使点D落在BC边上的点F处,已知AB=8,BC=10,求折痕AE的长。ABCDFE立体图形展开问题杜登尼(Dudeney,1857-1930年)是19世纪英国知名的谜题创作者.“蜘蛛和苍蝇”问题最早出现在1903年的英国报纸上,它是杜登尼最有名的谜题之一.它对全世界难题爱好者的挑战,长达四分之三个世纪.想挑战世纪谜题吗?立体图平面图化归ACB C C4m如图,有一棱长为4m的立方体房间,一只蜘蛛在A处. 最短
路程⑵若苍蝇在C处,则最短路程是多少? 4m4m⑴若一只苍蝇在B处,蜘蛛去抓苍蝇需要爬行的最短路程是多少? 变式四:如图,一圆柱体木块的底面周长为24cm,高AB为4cm ,BC是直径,一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程大约是( )
A.6cm B.12cm C.13cm D.16cm沿AB剪开策略迁移 ∵ 底面圆的周长为24cm ∴BB1=24cm
又∵点C 是BB1 的中点 ∴BC=12cm
而∵AB=4cm ∴ 在Rt△ABC中,根据勾股定理得: AC2=AB2+BC2 cm
∴选C
?
?
如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程( 取3)是( )
A.20cm B.10cm C.14cm D.无法确定 BB8OA2蛋糕ACB8周长的一半
6圆柱(锥)中的最值问题如图是一个三级台阶,它的每一级的长宽和高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,
A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿
着台阶面爬到B点最短路程是多少?
20232323ABC∵ AB2=AC2+BC2=625,
∴ AB=25.台阶中的最值问题
