17.2.1 勾股定理的逆定理 同步练习(含答案)
文档属性
| 名称 | 17.2.1 勾股定理的逆定理 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 112.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-10 10:30:35 | ||
图片预览

文档简介
第十七章 勾股定理
17.2 勾股定理的逆定理
第1课时 勾股定理的逆定理
一、选择题
1.命题“若a=b,则a2=b2”的逆命题是( )
A.若a2=b2,则a≠b B.若a=b,则a2≠b2
C.若a2≠b2,则a=b D.若a2=b2,则a=b
2.下列长度的四组线段中,可以构成直角三角形的是( )
A.1,2,3 B.,2, C.4,5,6 D.8,15,19
3.在△ABC中,若AC2-BC2=AB2,则( )
A.∠A=90° B.∠B=90° C.∠C=90° D.不能确定
4.如图,小正方形的边长均为1,A,B,C是小正方形的顶点,则∠ACB的度数是( )
A.30° B.45° C.60° D.75°
5.下列各组数是勾股数的一组是( )
A.2,3,4 B.5,12,13 C.1.5,2,2.5 D.
6.有五根小木棒,其长度(单位:cm)分别为8,9,12,15,17,现将它们摆成两个直角三角形,其中正确的是( )
二、填空题
7.“两直线平行,同位角相等”这个命题的逆命题是 ,其中原命题是 (填“真”或“假”)命题,逆命题是 (填“真”或“假”)命题.
8.如图,分别以△ABC的三边为边向外作正方形,它们的面积分别为2,3,5,则△ABC
直角三角形.(填“是”或“不是”)
9.有一组勾股数,已知其中的两个数分别是24和7,则第三个数是 .
10.观察下面几组勾股数,并寻找规律:
①4,3,5;②6,8,10;
③8,15,17;④10,24,26;
请你根据规律写出第⑤组勾股数是 .
11.如图,在△ABC中,AB=AC,D为AB上一点,连接CD,BD=5,CD=12,BC=12,则AB= .
12.若△ABC的三边长a,b,c满足条件(a-b)(a2+b2-c2)=0,则△ABC的形状是 .
三、解答题
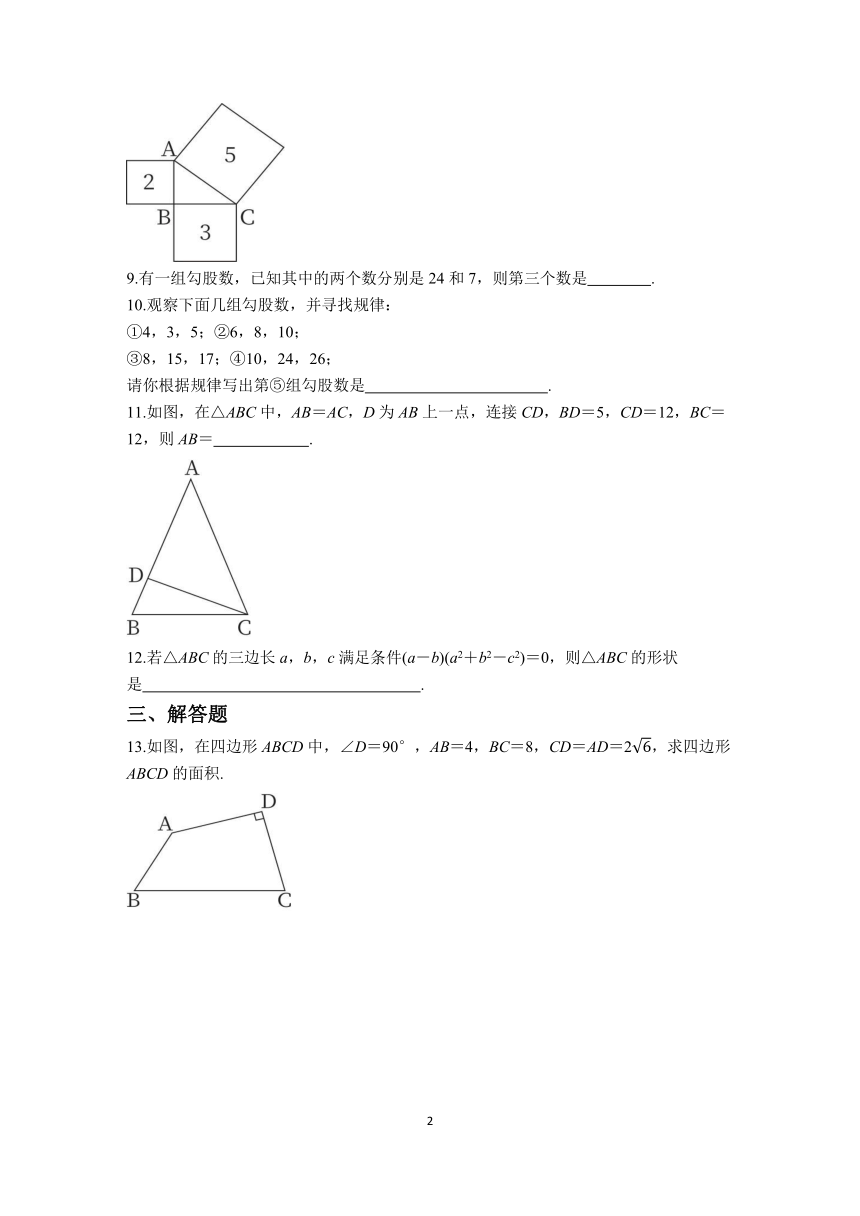
13.如图,在四边形ABCD中,∠D=90°,AB=4,BC=8,CD=AD=2,求四边形ABCD的面积.
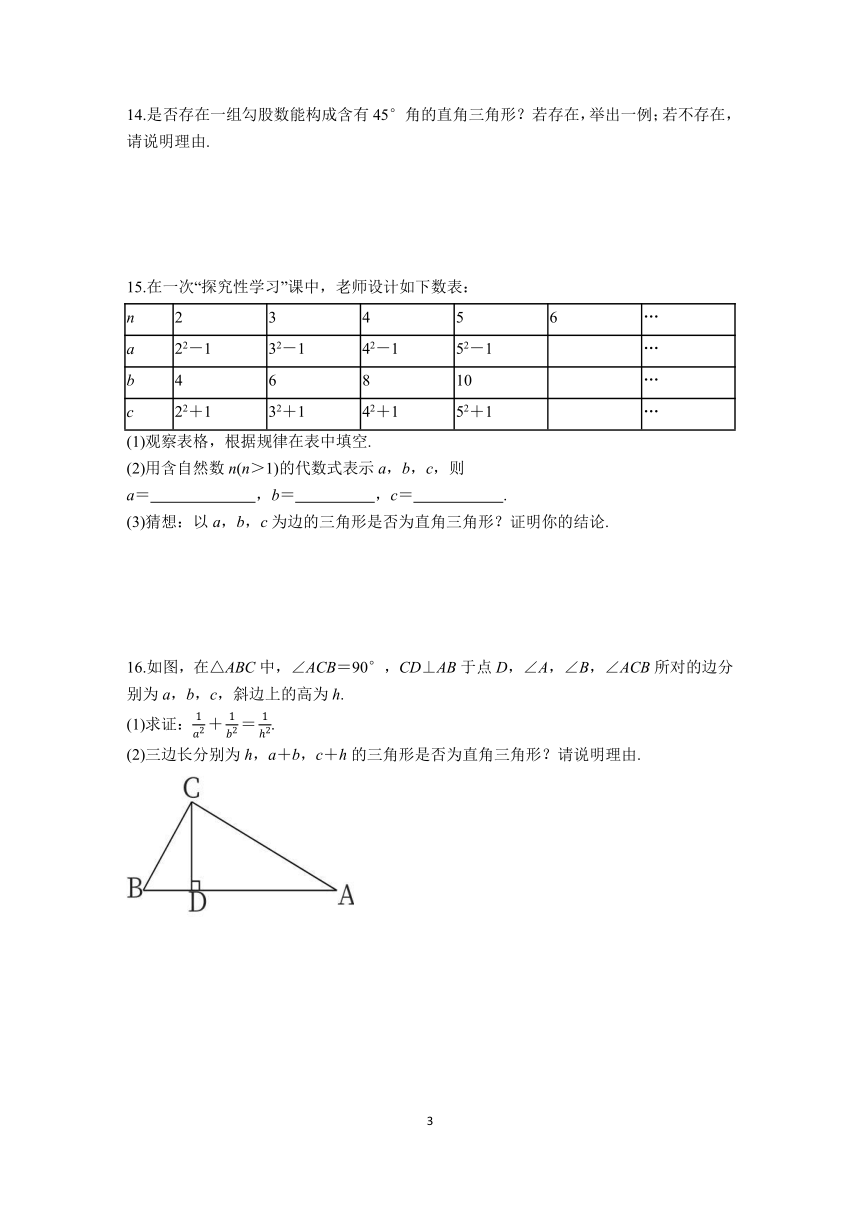
14.是否存在一组勾股数能构成含有45°角的直角三角形?若存在,举出一例;若不存在,请说明理由.
15.在一次“探究性学习”课中,老师设计如下数表:
n 2 3 4 5 6 …
a 22-1 32-1 42-1 52-1 …
b 4 6 8 10 …
c 22+1 32+1 42+1 52+1 …
(1)观察表格,根据规律在表中填空.
(2)用含自然数n(n>1)的代数式表示a,b,c,则
a= ,b= ,c= .
(3)猜想:以a,b,c为边的三角形是否为直角三角形?证明你的结论.
16.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,∠A,∠B,∠ACB所对的边分别为a,b,c,斜边上的高为h.
(1)求证:.
(2)三边长分别为h,a+b,c+h的三角形是否为直角三角形?请说明理由.
1
参考答案
一、选择题
1.命题“若a=b,则a2=b2”的逆命题是( D )
A.若a2=b2,则a≠b B.若a=b,则a2≠b2
C.若a2≠b2,则a=b D.若a2=b2,则a=b
2.下列长度的四组线段中,可以构成直角三角形的是( B )
A.1,2,3 B.,2, C.4,5,6 D.8,15,19
3.在△ABC中,若AC2-BC2=AB2,则( B )
A.∠A=90° B.∠B=90° C.∠C=90° D.不能确定
4.如图,小正方形的边长均为1,A,B,C是小正方形的顶点,则∠ACB的度数是( B )
A.30° B.45° C.60° D.75°
5.下列各组数是勾股数的一组是( B )
A.2,3,4 B.5,12,13 C.1.5,2,2.5 D.
6.有五根小木棒,其长度(单位:cm)分别为8,9,12,15,17,现将它们摆成两个直角三角形,其中正确的是( C )
二、填空题
7.“两直线平行,同位角相等”这个命题的逆命题是 ,其中原命题是 (填“真”或“假”)命题,逆命题是 (填“真”或“假”)命题.
【答案】同位角相等,两直线平行 真 真
8.如图,分别以△ABC的三边为边向外作正方形,它们的面积分别为2,3,5,则△ABC
直角三角形.(填“是”或“不是”)
【答案】是
9.有一组勾股数,已知其中的两个数分别是24和7,则第三个数是 .
【答案】25
10.观察下面几组勾股数,并寻找规律:
①4,3,5;②6,8,10;
③8,15,17;④10,24,26;
请你根据规律写出第⑤组勾股数是 .
【答案】 12,35,37
11.如图,在△ABC中,AB=AC,D为AB上一点,连接CD,BD=5,CD=12,BC=12,则AB= .
【答案】16.9
12.若△ABC的三边长a,b,c满足条件(a-b)(a2+b2-c2)=0,则△ABC的形状是 .
【答案】 等腰三角形或直角三角形
三、解答题
13.如图,在四边形ABCD中,∠D=90°,AB=4,BC=8,CD=AD=2,求四边形ABCD的面积.
解:连接AC.∵∠D=90°,CD=AD=2,
∴AC==4.
∵AB=4,BC=8,AC=4,
∴AB2=16,BC2=64,AC2=48,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,且∠BAC=90°,
∴S四边形ABCD=S△ABC+S△ADC=×4×4×2×2=8+12.
14.是否存在一组勾股数能构成含有45°角的直角三角形?若存在,举出一例;若不存在,请说明理由.
解:不存在任何一组勾股数能构成含有45°角的直角三角形.
理由:设45°角所对的直角边为a,则另外一条直角边为a,斜边为.
∵是无理数,
∴当a为正整数时,是无理数,a,a,不是勾股数,
∴不存在任何一组勾股数能构成含有45°角的直角三角形.
15.在一次“探究性学习”课中,老师设计如下数表:
n 2 3 4 5 6 …
a 22-1 32-1 42-1 52-1 …
b 4 6 8 10 …
c 22+1 32+1 42+1 52+1 …
(1)观察表格,根据规律在表中填空.
【答案】62-1 12 62+1
(2)用含自然数n(n>1)的代数式表示a,b,c,则
a= ,b= ,c= .
【答案】 n2-1 2n n2+1
(3)猜想:以a,b,c为边的三角形是否为直角三角形?证明你的结论.
解:(3)以a,b,c为边的三角形是直角三角形.
理由:
∵a2+b2=(n2-1)2+(2n)2=n4+2n2+1=(n2+1)2=c2,
∴以a,b,c为边的三角形是直角三角形.
16.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,∠A,∠B,∠ACB所对的边分别为a,b,c,斜边上的高为h.
(1)求证:.
(2)三边长分别为h,a+b,c+h的三角形是否为直角三角形?请说明理由.
解:(1)在Rt△ABC中,ab=ch,
∴(ab)2=(ch)2,即a2b2=c2h2.
∵a2+b2=c2,∴a2b2=(a2+b2)h2,
∴=h2,∴,
∴,∴.
(2)是.
理由:∵(c+h)2=c2+2ch+h2,a2+b2=c2,ab=ch,
∴c2+2ch+h2=a2+b2+2ab+h2=(a+b)2+h2,
即(c+h)2=(a+b)2+h2,
∴三边长分别为h,a+b,c+h的三角形是直角三角形.
17.2 勾股定理的逆定理
第1课时 勾股定理的逆定理
一、选择题
1.命题“若a=b,则a2=b2”的逆命题是( )
A.若a2=b2,则a≠b B.若a=b,则a2≠b2
C.若a2≠b2,则a=b D.若a2=b2,则a=b
2.下列长度的四组线段中,可以构成直角三角形的是( )
A.1,2,3 B.,2, C.4,5,6 D.8,15,19
3.在△ABC中,若AC2-BC2=AB2,则( )
A.∠A=90° B.∠B=90° C.∠C=90° D.不能确定
4.如图,小正方形的边长均为1,A,B,C是小正方形的顶点,则∠ACB的度数是( )
A.30° B.45° C.60° D.75°
5.下列各组数是勾股数的一组是( )
A.2,3,4 B.5,12,13 C.1.5,2,2.5 D.
6.有五根小木棒,其长度(单位:cm)分别为8,9,12,15,17,现将它们摆成两个直角三角形,其中正确的是( )
二、填空题
7.“两直线平行,同位角相等”这个命题的逆命题是 ,其中原命题是 (填“真”或“假”)命题,逆命题是 (填“真”或“假”)命题.
8.如图,分别以△ABC的三边为边向外作正方形,它们的面积分别为2,3,5,则△ABC
直角三角形.(填“是”或“不是”)
9.有一组勾股数,已知其中的两个数分别是24和7,则第三个数是 .
10.观察下面几组勾股数,并寻找规律:
①4,3,5;②6,8,10;
③8,15,17;④10,24,26;
请你根据规律写出第⑤组勾股数是 .
11.如图,在△ABC中,AB=AC,D为AB上一点,连接CD,BD=5,CD=12,BC=12,则AB= .
12.若△ABC的三边长a,b,c满足条件(a-b)(a2+b2-c2)=0,则△ABC的形状是 .
三、解答题
13.如图,在四边形ABCD中,∠D=90°,AB=4,BC=8,CD=AD=2,求四边形ABCD的面积.
14.是否存在一组勾股数能构成含有45°角的直角三角形?若存在,举出一例;若不存在,请说明理由.
15.在一次“探究性学习”课中,老师设计如下数表:
n 2 3 4 5 6 …
a 22-1 32-1 42-1 52-1 …
b 4 6 8 10 …
c 22+1 32+1 42+1 52+1 …
(1)观察表格,根据规律在表中填空.
(2)用含自然数n(n>1)的代数式表示a,b,c,则
a= ,b= ,c= .
(3)猜想:以a,b,c为边的三角形是否为直角三角形?证明你的结论.
16.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,∠A,∠B,∠ACB所对的边分别为a,b,c,斜边上的高为h.
(1)求证:.
(2)三边长分别为h,a+b,c+h的三角形是否为直角三角形?请说明理由.
1
参考答案
一、选择题
1.命题“若a=b,则a2=b2”的逆命题是( D )
A.若a2=b2,则a≠b B.若a=b,则a2≠b2
C.若a2≠b2,则a=b D.若a2=b2,则a=b
2.下列长度的四组线段中,可以构成直角三角形的是( B )
A.1,2,3 B.,2, C.4,5,6 D.8,15,19
3.在△ABC中,若AC2-BC2=AB2,则( B )
A.∠A=90° B.∠B=90° C.∠C=90° D.不能确定
4.如图,小正方形的边长均为1,A,B,C是小正方形的顶点,则∠ACB的度数是( B )
A.30° B.45° C.60° D.75°
5.下列各组数是勾股数的一组是( B )
A.2,3,4 B.5,12,13 C.1.5,2,2.5 D.
6.有五根小木棒,其长度(单位:cm)分别为8,9,12,15,17,现将它们摆成两个直角三角形,其中正确的是( C )
二、填空题
7.“两直线平行,同位角相等”这个命题的逆命题是 ,其中原命题是 (填“真”或“假”)命题,逆命题是 (填“真”或“假”)命题.
【答案】同位角相等,两直线平行 真 真
8.如图,分别以△ABC的三边为边向外作正方形,它们的面积分别为2,3,5,则△ABC
直角三角形.(填“是”或“不是”)
【答案】是
9.有一组勾股数,已知其中的两个数分别是24和7,则第三个数是 .
【答案】25
10.观察下面几组勾股数,并寻找规律:
①4,3,5;②6,8,10;
③8,15,17;④10,24,26;
请你根据规律写出第⑤组勾股数是 .
【答案】 12,35,37
11.如图,在△ABC中,AB=AC,D为AB上一点,连接CD,BD=5,CD=12,BC=12,则AB= .
【答案】16.9
12.若△ABC的三边长a,b,c满足条件(a-b)(a2+b2-c2)=0,则△ABC的形状是 .
【答案】 等腰三角形或直角三角形
三、解答题
13.如图,在四边形ABCD中,∠D=90°,AB=4,BC=8,CD=AD=2,求四边形ABCD的面积.
解:连接AC.∵∠D=90°,CD=AD=2,
∴AC==4.
∵AB=4,BC=8,AC=4,
∴AB2=16,BC2=64,AC2=48,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,且∠BAC=90°,
∴S四边形ABCD=S△ABC+S△ADC=×4×4×2×2=8+12.
14.是否存在一组勾股数能构成含有45°角的直角三角形?若存在,举出一例;若不存在,请说明理由.
解:不存在任何一组勾股数能构成含有45°角的直角三角形.
理由:设45°角所对的直角边为a,则另外一条直角边为a,斜边为.
∵是无理数,
∴当a为正整数时,是无理数,a,a,不是勾股数,
∴不存在任何一组勾股数能构成含有45°角的直角三角形.
15.在一次“探究性学习”课中,老师设计如下数表:
n 2 3 4 5 6 …
a 22-1 32-1 42-1 52-1 …
b 4 6 8 10 …
c 22+1 32+1 42+1 52+1 …
(1)观察表格,根据规律在表中填空.
【答案】62-1 12 62+1
(2)用含自然数n(n>1)的代数式表示a,b,c,则
a= ,b= ,c= .
【答案】 n2-1 2n n2+1
(3)猜想:以a,b,c为边的三角形是否为直角三角形?证明你的结论.
解:(3)以a,b,c为边的三角形是直角三角形.
理由:
∵a2+b2=(n2-1)2+(2n)2=n4+2n2+1=(n2+1)2=c2,
∴以a,b,c为边的三角形是直角三角形.
16.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,∠A,∠B,∠ACB所对的边分别为a,b,c,斜边上的高为h.
(1)求证:.
(2)三边长分别为h,a+b,c+h的三角形是否为直角三角形?请说明理由.
解:(1)在Rt△ABC中,ab=ch,
∴(ab)2=(ch)2,即a2b2=c2h2.
∵a2+b2=c2,∴a2b2=(a2+b2)h2,
∴=h2,∴,
∴,∴.
(2)是.
理由:∵(c+h)2=c2+2ch+h2,a2+b2=c2,ab=ch,
∴c2+2ch+h2=a2+b2+2ab+h2=(a+b)2+h2,
即(c+h)2=(a+b)2+h2,
∴三边长分别为h,a+b,c+h的三角形是直角三角形.
