17.2.2 勾股定理的逆定理的应用 同步练习(含答案解析)
文档属性
| 名称 | 17.2.2 勾股定理的逆定理的应用 同步练习(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 167.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-10 10:31:45 | ||
图片预览


文档简介
第十七章 勾股定理
17.2 勾股定理的逆定理
第2课时 勾股定理的逆定理的应用
一、选择题
1.木工师傅想利用木条制作一个直角三角形的工具,那么下列各组数据(单位:米)不符合直角三角形的三边长的是( )
A.1,2,3 B.3,4,5 C.7,24,25 D.9,12,15
2.如图,某海域有相距10海里的两个小岛A和C,甲船先由A岛沿北偏东70°方向走了8海里到达B岛,然后再从B岛走了6海里到达C岛,此时甲船位于B岛的( )
A.北偏东20°方向上B.北偏西20°方向上
C.北偏西30°方向上D.北偏西40°方向上
3.一辆汽车从点A出发沿正东方向行驶30 km到达点B,然后转向行驶40 km到达点C,最后从点C沿CA方向直接回到出发点A.如果汽车从出发到返回共行驶了120 km,那么BC的方向是( )
A.正东或正西 B.正南 C.正北 D.正南或正北
4.如图,在正方形网格内,A,B,C,D四点都在小方格的格点(网格线的交点)上,则∠BAC+∠DAC=( )
A.30° B.45°C.60° D.75°
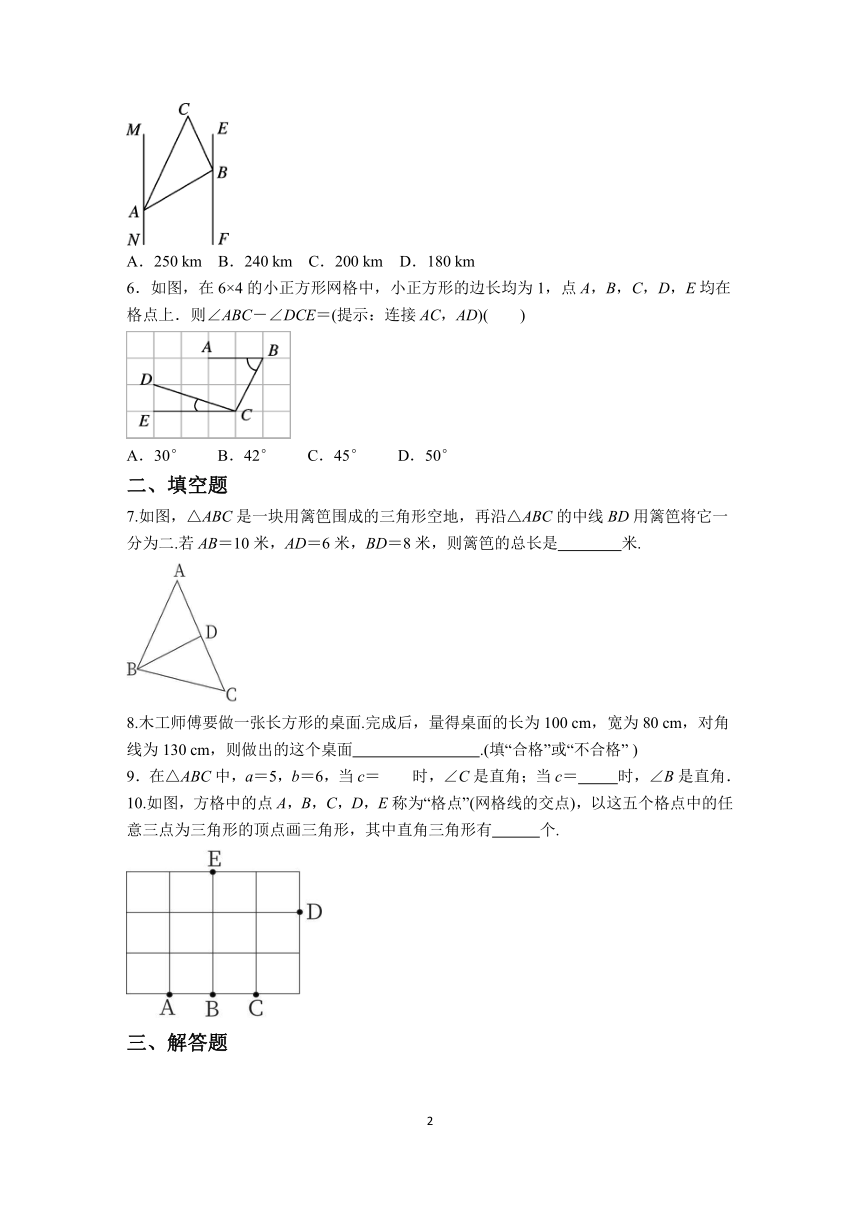
5.如图,A,B两个村庄分别在两条公路MN和EF的边上,且MN∥EF,某施工队在A,B,C三个村之间修了三条笔直的路.若∠MAB=65°,∠CBE=25°,AB=160 km,BC=120 km,则A,C两村之间的距离为( )
A.250 km B.240 km C.200 km D.180 km
6.如图,在6×4的小正方形网格中,小正方形的边长均为1,点A,B,C,D,E均在格点上.则∠ABC-∠DCE=(提示:连接AC,AD)( )
A.30° B.42° C.45° D.50°
二、填空题
7.如图,△ABC是一块用篱笆围成的三角形空地,再沿△ABC的中线BD用篱笆将它一分为二.若AB=10米,AD=6米,BD=8米,则篱笆的总长是 米.
8.木工师傅要做一张长方形的桌面.完成后,量得桌面的长为100 cm,宽为80 cm,对角线为130 cm,则做出的这个桌面 .(填“合格”或“不合格” )
9.在△ABC中,a=5,b=6,当c= 时,∠C是直角;当c= 时,∠B是直角.
10.如图,方格中的点A,B,C,D,E称为“格点”(网格线的交点),以这五个格点中的任意三点为三角形的顶点画三角形,其中直角三角形有 个.
三、解答题
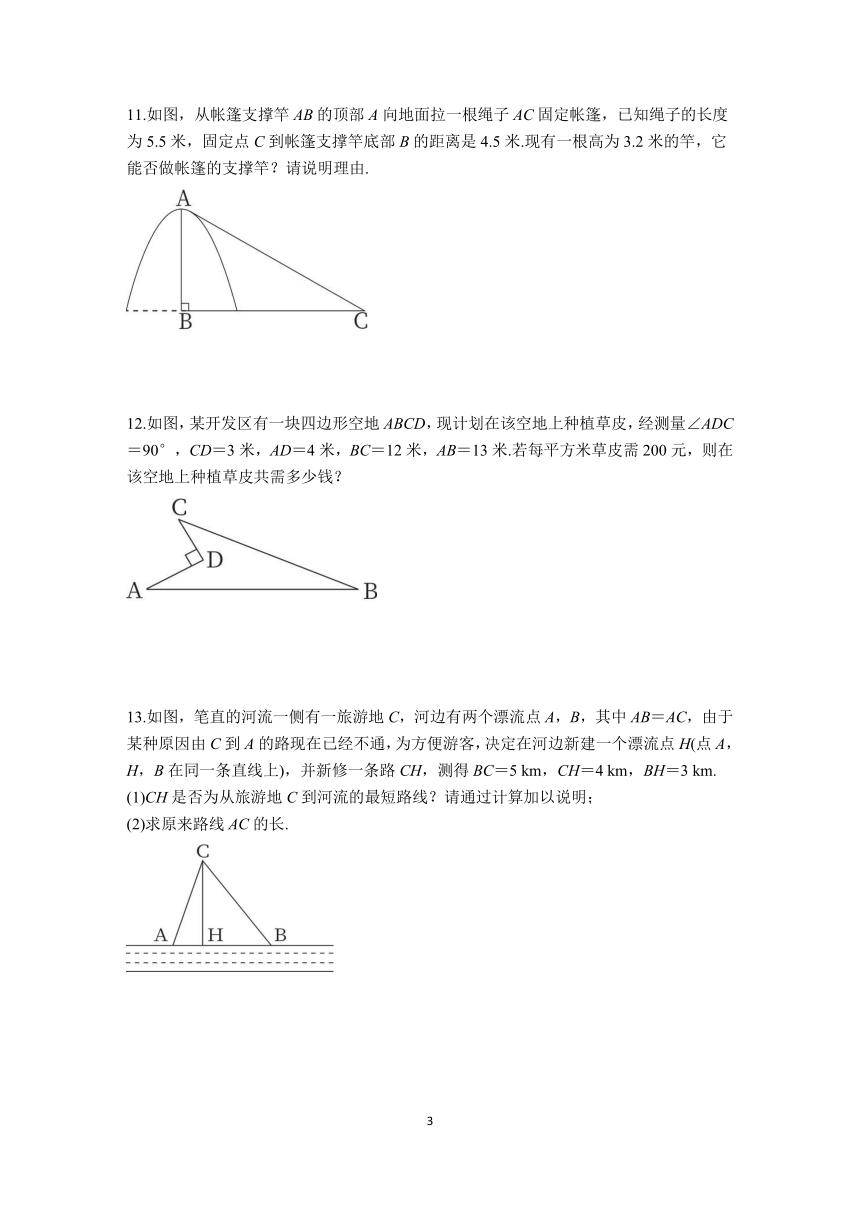
11.如图,从帐篷支撑竿AB的顶部A向地面拉一根绳子AC固定帐篷,已知绳子的长度为5.5米,固定点C到帐篷支撑竿底部B的距离是4.5米.现有一根高为3.2米的竿,它能否做帐篷的支撑竿?请说明理由.
12.如图,某开发区有一块四边形空地ABCD,现计划在该空地上种植草皮,经测量∠ADC=90°,CD=3米,AD=4米,BC=12米,AB=13米.若每平方米草皮需200元,则在该空地上种植草皮共需多少钱?
13.如图,笔直的河流一侧有一旅游地C,河边有两个漂流点A,B,其中AB=AC,由于某种原因由C到A的路现在已经不通,为方便游客,决定在河边新建一个漂流点H(点A,H,B在同一条直线上),并新修一条路CH,测得BC=5 km,CH=4 km,BH=3 km.
(1)CH是否为从旅游地C到河流的最短路线?请通过计算加以说明;
(2)求原来路线AC的长.
14.如图,台风中心沿东西方向AB由点A向点B移动,已知点C为一海港,且点C与直线AB上的两点A,B的距离分别为AC=300 km,BC=400 km,且AB=500 km,经测量,距离台风中心260 km及以内的地区会受到影响.
(1)求∠ACB的度数.
(2)海港C受台风影响吗?为什么?
(3)若台风中心的移动速度为28 km/h,则台风影响该海港持续的时间有多长?
1
参考答案
一、选择题
1.木工师傅想利用木条制作一个直角三角形的工具,那么下列各组数据(单位:米)不符合直角三角形的三边长的是( A )
A.1,2,3 B.3,4,5 C.7,24,25 D.9,12,15
2.如图,某海域有相距10海里的两个小岛A和C,甲船先由A岛沿北偏东70°方向走了8海里到达B岛,然后再从B岛走了6海里到达C岛,此时甲船位于B岛的( B )
A.北偏东20°方向上B.北偏西20°方向上
C.北偏西30°方向上D.北偏西40°方向上
3.一辆汽车从点A出发沿正东方向行驶30 km到达点B,然后转向行驶40 km到达点C,最后从点C沿CA方向直接回到出发点A.如果汽车从出发到返回共行驶了120 km,那么BC的方向是( D )
A.正东或正西 B.正南 C.正北 D.正南或正北
4.如图,在正方形网格内,A,B,C,D四点都在小方格的格点(网格线的交点)上,则∠BAC+∠DAC=( B )
A.30° B.45°C.60° D.75°
5.如图,A,B两个村庄分别在两条公路MN和EF的边上,且MN∥EF,某施工队在A,B,C三个村之间修了三条笔直的路.若∠MAB=65°,∠CBE=25°,AB=160 km,BC=120 km,则A,C两村之间的距离为( C )
A.250 km B.240 km C.200 km D.180 km
6.如图,在6×4的小正方形网格中,小正方形的边长均为1,点A,B,C,D,E均在格点上.则∠ABC-∠DCE=(提示:连接AC,AD)( C )
A.30° B.42° C.45° D.50°
【解析】连接AC,AD,如图,根据勾股定理可得AD=AC=BC=,CD=,∴∠ABC=∠BAC,在△ACD中,AD2+AC2=()2+()2=10,CD2=()2=10,∴AD2+AC2=CD2,∴△ACD是直角三角形,∠DAC=90°,∵AD=CD,∴△ACD是等腰直角三角形,∴∠ACD=45°,∵AB∥EC,∴∠BAC=∠ACE,∴∠ABC-∠DCE=∠BAC-∠DCE=∠ACE-∠DCE=∠ACD=45°.
二、填空题
7.如图,△ABC是一块用篱笆围成的三角形空地,再沿△ABC的中线BD用篱笆将它一分为二.若AB=10米,AD=6米,BD=8米,则篱笆的总长是 米.
【答案】40
8.木工师傅要做一张长方形的桌面.完成后,量得桌面的长为100 cm,宽为80 cm,对角线为130 cm,则做出的这个桌面 .(填“合格”或“不合格” )
【答案】不合格
9.在△ABC中,a=5,b=6,当c= 时,∠C是直角;当c= 时,∠B是直角.
【答案】
10.如图,方格中的点A,B,C,D,E称为“格点”(网格线的交点),以这五个格点中的任意三点为三角形的顶点画三角形,其中直角三角形有 个.
【答案】3
三、解答题
11.如图,从帐篷支撑竿AB的顶部A向地面拉一根绳子AC固定帐篷,已知绳子的长度为5.5米,固定点C到帐篷支撑竿底部B的距离是4.5米.现有一根高为3.2米的竿,它能否做帐篷的支撑竿?请说明理由.
解:因为在△ABC中,AC=5.5,BC=4.5,AB=3.2,
所以AC2=30.25,BC2=20.25,AB2=10.24.
因为30.25≠20.25+10.24,
所以它不能做帐篷的支撑竿.
12.如图,某开发区有一块四边形空地ABCD,现计划在该空地上种植草皮,经测量∠ADC=90°,CD=3米,AD=4米,BC=12米,AB=13米.若每平方米草皮需200元,则在该空地上种植草皮共需多少钱?
解:连接AC.在Rt△ACD中,AC==5.
在△ABC中,∵52+122=132,
∴AC2+BC2=AB2,∴∠ACB=90°,
∴S四边形ABCD=S△ABC-S△ACD=·BC-·CD=×5×12-×4×3=24(米2),24×200=4800(元).
答:在该空地上种植草皮共需4800元.
13.如图,笔直的河流一侧有一旅游地C,河边有两个漂流点A,B,其中AB=AC,由于某种原因由C到A的路现在已经不通,为方便游客,决定在河边新建一个漂流点H(点A,H,B在同一条直线上),并新修一条路CH,测得BC=5 km,CH=4 km,BH=3 km.
(1)CH是否为从旅游地C到河流的最短路线?请通过计算加以说明;
(2)求原来路线AC的长.
解:(1)CH是从旅游地C到河流的最短路线.
理由是:在△CHB中,
∵CH2+BH2=42+32=25,BC2=25,∴CH2+BH2=BC2,
∴△CHB是直角三角形,且∠CHB=90°,
∴CH⊥AB,
∴CH是从旅游地C到河流的最短路线.
(2)设AC=x,则AH=x-3.
在Rt△ACH中,AC2=AH2+CH2,
即x2=(x-3)2+42,解得x=.
答:原来路线AC的长为 km.
14.如图,台风中心沿东西方向AB由点A向点B移动,已知点C为一海港,且点C与直线AB上的两点A,B的距离分别为AC=300 km,BC=400 km,且AB=500 km,经测量,距离台风中心260 km及以内的地区会受到影响.
(1)求∠ACB的度数.
(2)海港C受台风影响吗?为什么?
(3)若台风中心的移动速度为28 km/h,则台风影响该海港持续的时间有多长?
解:(1)∵AC=300,BC=400,AB=500,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠ACB=90°.
(2)海港C受台风影响.
理由是:过点C作CD⊥AB于点D.
∵△ABC是直角三角形,
∴AC·BC=AB·CD,
即300×400=500CD,
∴CD=240 km,
∵距离台风中心260 km及以内为受影响区域,
∴海港C受台风影响.
(3)如图,当EC=260,FC=260时,台风正好影响C港口.
∵ED==100,
∴EF=2ED=200,
∵台风中心的移动速度为28 km/h,
∴200÷28=(h).
答:台风影响该海港持续的时间为 h.
17.2 勾股定理的逆定理
第2课时 勾股定理的逆定理的应用
一、选择题
1.木工师傅想利用木条制作一个直角三角形的工具,那么下列各组数据(单位:米)不符合直角三角形的三边长的是( )
A.1,2,3 B.3,4,5 C.7,24,25 D.9,12,15
2.如图,某海域有相距10海里的两个小岛A和C,甲船先由A岛沿北偏东70°方向走了8海里到达B岛,然后再从B岛走了6海里到达C岛,此时甲船位于B岛的( )
A.北偏东20°方向上B.北偏西20°方向上
C.北偏西30°方向上D.北偏西40°方向上
3.一辆汽车从点A出发沿正东方向行驶30 km到达点B,然后转向行驶40 km到达点C,最后从点C沿CA方向直接回到出发点A.如果汽车从出发到返回共行驶了120 km,那么BC的方向是( )
A.正东或正西 B.正南 C.正北 D.正南或正北
4.如图,在正方形网格内,A,B,C,D四点都在小方格的格点(网格线的交点)上,则∠BAC+∠DAC=( )
A.30° B.45°C.60° D.75°
5.如图,A,B两个村庄分别在两条公路MN和EF的边上,且MN∥EF,某施工队在A,B,C三个村之间修了三条笔直的路.若∠MAB=65°,∠CBE=25°,AB=160 km,BC=120 km,则A,C两村之间的距离为( )
A.250 km B.240 km C.200 km D.180 km
6.如图,在6×4的小正方形网格中,小正方形的边长均为1,点A,B,C,D,E均在格点上.则∠ABC-∠DCE=(提示:连接AC,AD)( )
A.30° B.42° C.45° D.50°
二、填空题
7.如图,△ABC是一块用篱笆围成的三角形空地,再沿△ABC的中线BD用篱笆将它一分为二.若AB=10米,AD=6米,BD=8米,则篱笆的总长是 米.
8.木工师傅要做一张长方形的桌面.完成后,量得桌面的长为100 cm,宽为80 cm,对角线为130 cm,则做出的这个桌面 .(填“合格”或“不合格” )
9.在△ABC中,a=5,b=6,当c= 时,∠C是直角;当c= 时,∠B是直角.
10.如图,方格中的点A,B,C,D,E称为“格点”(网格线的交点),以这五个格点中的任意三点为三角形的顶点画三角形,其中直角三角形有 个.
三、解答题
11.如图,从帐篷支撑竿AB的顶部A向地面拉一根绳子AC固定帐篷,已知绳子的长度为5.5米,固定点C到帐篷支撑竿底部B的距离是4.5米.现有一根高为3.2米的竿,它能否做帐篷的支撑竿?请说明理由.
12.如图,某开发区有一块四边形空地ABCD,现计划在该空地上种植草皮,经测量∠ADC=90°,CD=3米,AD=4米,BC=12米,AB=13米.若每平方米草皮需200元,则在该空地上种植草皮共需多少钱?
13.如图,笔直的河流一侧有一旅游地C,河边有两个漂流点A,B,其中AB=AC,由于某种原因由C到A的路现在已经不通,为方便游客,决定在河边新建一个漂流点H(点A,H,B在同一条直线上),并新修一条路CH,测得BC=5 km,CH=4 km,BH=3 km.
(1)CH是否为从旅游地C到河流的最短路线?请通过计算加以说明;
(2)求原来路线AC的长.
14.如图,台风中心沿东西方向AB由点A向点B移动,已知点C为一海港,且点C与直线AB上的两点A,B的距离分别为AC=300 km,BC=400 km,且AB=500 km,经测量,距离台风中心260 km及以内的地区会受到影响.
(1)求∠ACB的度数.
(2)海港C受台风影响吗?为什么?
(3)若台风中心的移动速度为28 km/h,则台风影响该海港持续的时间有多长?
1
参考答案
一、选择题
1.木工师傅想利用木条制作一个直角三角形的工具,那么下列各组数据(单位:米)不符合直角三角形的三边长的是( A )
A.1,2,3 B.3,4,5 C.7,24,25 D.9,12,15
2.如图,某海域有相距10海里的两个小岛A和C,甲船先由A岛沿北偏东70°方向走了8海里到达B岛,然后再从B岛走了6海里到达C岛,此时甲船位于B岛的( B )
A.北偏东20°方向上B.北偏西20°方向上
C.北偏西30°方向上D.北偏西40°方向上
3.一辆汽车从点A出发沿正东方向行驶30 km到达点B,然后转向行驶40 km到达点C,最后从点C沿CA方向直接回到出发点A.如果汽车从出发到返回共行驶了120 km,那么BC的方向是( D )
A.正东或正西 B.正南 C.正北 D.正南或正北
4.如图,在正方形网格内,A,B,C,D四点都在小方格的格点(网格线的交点)上,则∠BAC+∠DAC=( B )
A.30° B.45°C.60° D.75°
5.如图,A,B两个村庄分别在两条公路MN和EF的边上,且MN∥EF,某施工队在A,B,C三个村之间修了三条笔直的路.若∠MAB=65°,∠CBE=25°,AB=160 km,BC=120 km,则A,C两村之间的距离为( C )
A.250 km B.240 km C.200 km D.180 km
6.如图,在6×4的小正方形网格中,小正方形的边长均为1,点A,B,C,D,E均在格点上.则∠ABC-∠DCE=(提示:连接AC,AD)( C )
A.30° B.42° C.45° D.50°
【解析】连接AC,AD,如图,根据勾股定理可得AD=AC=BC=,CD=,∴∠ABC=∠BAC,在△ACD中,AD2+AC2=()2+()2=10,CD2=()2=10,∴AD2+AC2=CD2,∴△ACD是直角三角形,∠DAC=90°,∵AD=CD,∴△ACD是等腰直角三角形,∴∠ACD=45°,∵AB∥EC,∴∠BAC=∠ACE,∴∠ABC-∠DCE=∠BAC-∠DCE=∠ACE-∠DCE=∠ACD=45°.
二、填空题
7.如图,△ABC是一块用篱笆围成的三角形空地,再沿△ABC的中线BD用篱笆将它一分为二.若AB=10米,AD=6米,BD=8米,则篱笆的总长是 米.
【答案】40
8.木工师傅要做一张长方形的桌面.完成后,量得桌面的长为100 cm,宽为80 cm,对角线为130 cm,则做出的这个桌面 .(填“合格”或“不合格” )
【答案】不合格
9.在△ABC中,a=5,b=6,当c= 时,∠C是直角;当c= 时,∠B是直角.
【答案】
10.如图,方格中的点A,B,C,D,E称为“格点”(网格线的交点),以这五个格点中的任意三点为三角形的顶点画三角形,其中直角三角形有 个.
【答案】3
三、解答题
11.如图,从帐篷支撑竿AB的顶部A向地面拉一根绳子AC固定帐篷,已知绳子的长度为5.5米,固定点C到帐篷支撑竿底部B的距离是4.5米.现有一根高为3.2米的竿,它能否做帐篷的支撑竿?请说明理由.
解:因为在△ABC中,AC=5.5,BC=4.5,AB=3.2,
所以AC2=30.25,BC2=20.25,AB2=10.24.
因为30.25≠20.25+10.24,
所以它不能做帐篷的支撑竿.
12.如图,某开发区有一块四边形空地ABCD,现计划在该空地上种植草皮,经测量∠ADC=90°,CD=3米,AD=4米,BC=12米,AB=13米.若每平方米草皮需200元,则在该空地上种植草皮共需多少钱?
解:连接AC.在Rt△ACD中,AC==5.
在△ABC中,∵52+122=132,
∴AC2+BC2=AB2,∴∠ACB=90°,
∴S四边形ABCD=S△ABC-S△ACD=·BC-·CD=×5×12-×4×3=24(米2),24×200=4800(元).
答:在该空地上种植草皮共需4800元.
13.如图,笔直的河流一侧有一旅游地C,河边有两个漂流点A,B,其中AB=AC,由于某种原因由C到A的路现在已经不通,为方便游客,决定在河边新建一个漂流点H(点A,H,B在同一条直线上),并新修一条路CH,测得BC=5 km,CH=4 km,BH=3 km.
(1)CH是否为从旅游地C到河流的最短路线?请通过计算加以说明;
(2)求原来路线AC的长.
解:(1)CH是从旅游地C到河流的最短路线.
理由是:在△CHB中,
∵CH2+BH2=42+32=25,BC2=25,∴CH2+BH2=BC2,
∴△CHB是直角三角形,且∠CHB=90°,
∴CH⊥AB,
∴CH是从旅游地C到河流的最短路线.
(2)设AC=x,则AH=x-3.
在Rt△ACH中,AC2=AH2+CH2,
即x2=(x-3)2+42,解得x=.
答:原来路线AC的长为 km.
14.如图,台风中心沿东西方向AB由点A向点B移动,已知点C为一海港,且点C与直线AB上的两点A,B的距离分别为AC=300 km,BC=400 km,且AB=500 km,经测量,距离台风中心260 km及以内的地区会受到影响.
(1)求∠ACB的度数.
(2)海港C受台风影响吗?为什么?
(3)若台风中心的移动速度为28 km/h,则台风影响该海港持续的时间有多长?
解:(1)∵AC=300,BC=400,AB=500,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠ACB=90°.
(2)海港C受台风影响.
理由是:过点C作CD⊥AB于点D.
∵△ABC是直角三角形,
∴AC·BC=AB·CD,
即300×400=500CD,
∴CD=240 km,
∵距离台风中心260 km及以内为受影响区域,
∴海港C受台风影响.
(3)如图,当EC=260,FC=260时,台风正好影响C港口.
∵ED==100,
∴EF=2ED=200,
∵台风中心的移动速度为28 km/h,
∴200÷28=(h).
答:台风影响该海港持续的时间为 h.
