人教版 数学五年级下册 长方体和正方体的表面积同步练习 (含答案)
文档属性
| 名称 | 人教版 数学五年级下册 长方体和正方体的表面积同步练习 (含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 222.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-10 00:00:00 | ||
图片预览

文档简介
小学数学五下长方体和正方体的表面积作业
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.如图是一个正方体盒子,下面的图( )是这个正方体盒子的展开图。
A. B. C. D.
2.“仁、义、礼、智、信、孝”是我国的传统美德,小明将这六个字分别写在一个正方体的六个面上,下图是这个正方体的平面展开图,在这个正方体中,和“礼”相对的字是( )。
A.“仁” B.“智” C.“信” D.“孝”
3.把一个长6分米,宽5分米,高3分米的长方体切成两个同样的小长方体,表面积最多增加( )平方分米。
A.90 B.30 C.36 D.60
4.把4个棱长1厘米的正方体排成一排,变成一个长方体,表面积比原来减少( )平方厘米。
A.4 B.6 C.8 D.3
5.两个一样的正方体,拼成一个长方体,表面积( )。
A.增加了 B.减少了 C.不变 D.无法确定
6.如果把4个礼品盒包装在一起,下面几种方法中,最节省包装纸的是( )。
A. B.
C. D.
7.下面四个图形中,不是正方体表面展开图的是( )。
A. B.
C. D.
8.如图所示的物体是由23块棱长为1cm的正方体积木拼搭而成,如果拿走其中的一块,那么剩下物体的表面积与原来相比,不可能是( )。
A.不变的 B.减少 C.减少 D.增加
9.一个长方体水池,长20米,宽10米,深2米,占地( )平方米。
A.200 B.400 C.520
二、填空题
10.把两个长、宽、高分别是10厘米、8厘米、2厘米的相同长方体拼成一个大长方体,这个大长方体的表面积最少是( )平方厘米。
11.焊接一个正方体框架共用去铁丝60cm,这个正方体的棱长是( )cm,在这个框架的四面粘贴彩纸,至少需要彩纸是( )cm2。
12.如图:
(1)两个完全相同的正方体拼在一起,表面积减少( )个面,三个正方体拼在一起减少( )个面;每增加一个正方体减少( )面。
(2)n个小正方体拼在一起减少( )面。
(3)如果小正方体的棱长是1厘米,5个小正方体如上图一样拼在一起表面积是( )平方厘米,n个小正方体拼在一起表面积是( )平方厘米。
三、判断题
13.这个图形能围成一个正方体。( )
14.下面是一个长方体表面展开图。( )
15.正方体的表面积比长方体的表面积小。( )
16.从一个长方体的顶点处切下一个小正方体后,剩下的物体的表面积不变。( )
17.把两个棱长都是a分米的正方体拼成一个长方体,拼成的这个长方体的表面积是12a2平方分米。( )
四、计算题
18.求下面图形的表面积。
(1)上面的面积:
(2)前面的面积:
(3)右面的面积:
(4)长方体的表面积:
19.求出下面正方体的表面积。
20.计算下面立体图形的表面积和体积。(单位:dm)
五、解答题
21.某古建筑景点定做了25个宫灯(如图,单位:厘米)。宫灯外侧有一层外饰面(上、下面除外)。如果外饰面每平方米18元,这些宫灯的外饰面一共要花多少钱?
22.把一个棱长46厘米的正方体纸箱各面都贴上红纸,作为捐款箱。
(1)至少需要多少平方厘米的红纸?(开口处忽略不计。)
(2)如果只在棱上粘贴一圈胶带纸,一卷4.5米长的胶带纸够用吗?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
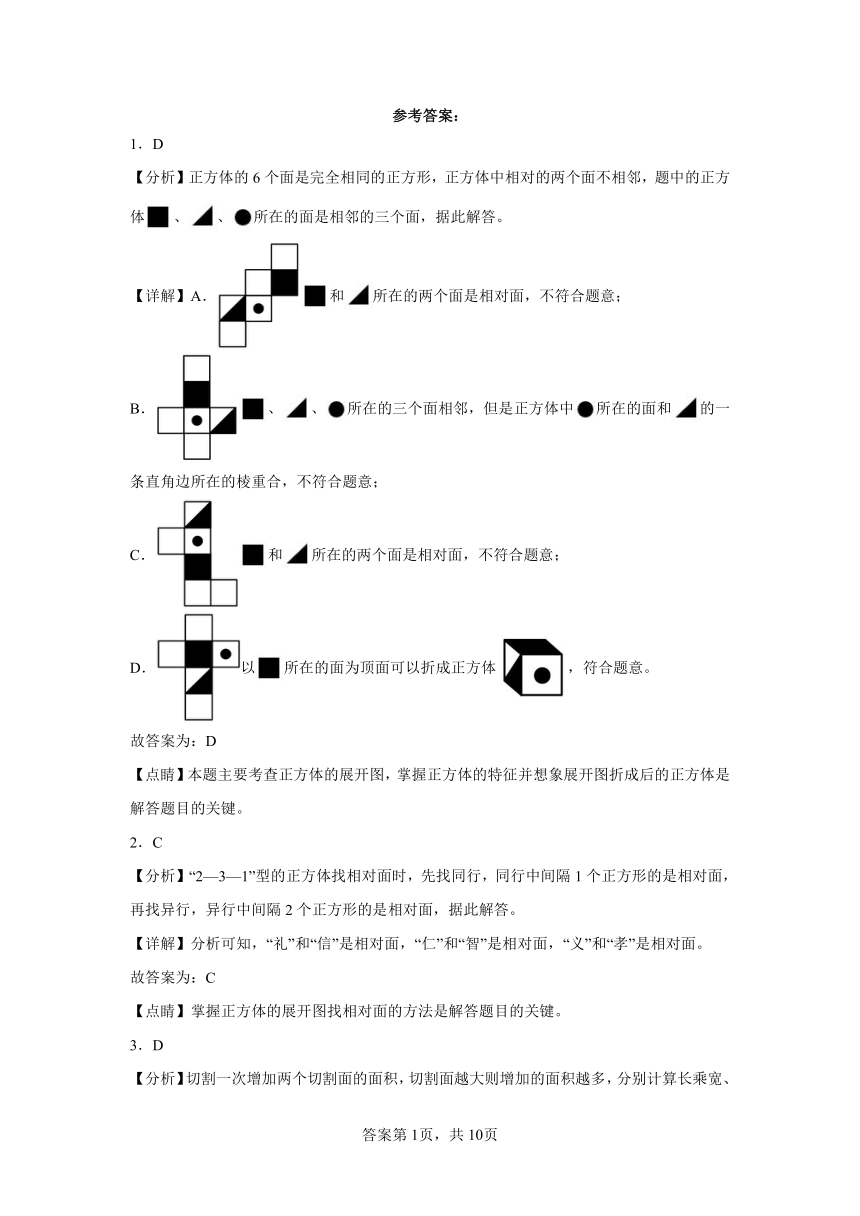
1.D
【分析】正方体的6个面是完全相同的正方形,正方体中相对的两个面不相邻,题中的正方体、、所在的面是相邻的三个面,据此解答。
【详解】A.和所在的两个面是相对面,不符合题意;
B.、、所在的三个面相邻,但是正方体中所在的面和的一条直角边所在的棱重合,不符合题意;
C.和所在的两个面是相对面,不符合题意;
D.以所在的面为顶面可以折成正方体,符合题意。
故答案为:D
【点睛】本题主要考查正方体的展开图,掌握正方体的特征并想象展开图折成后的正方体是解答题目的关键。
2.C
【分析】“2—3—1”型的正方体找相对面时,先找同行,同行中间隔1个正方形的是相对面,再找异行,异行中间隔2个正方形的是相对面,据此解答。
【详解】分析可知,“礼”和“信”是相对面,“仁”和“智”是相对面,“义”和“孝”是相对面。
故答案为:C
【点睛】掌握正方体的展开图找相对面的方法是解答题目的关键。
3.D
【分析】切割一次增加两个切割面的面积,切割面越大则增加的面积越多,分别计算长乘宽、长乘高以及宽乘高的面分别是多大,选最大的面作为切割面,据此分析求解。
【详解】5×6=30(平方分米)
3×6=18(平方分米)
3×5=15(平方分米)
30>18>15
30×2=60(平方分米)
表面积最多增加60平方分米。
故答案为:D
【点睛】明确切割一次增加两个面是解题的关键。
4.B
【分析】如下图:把4个棱长1厘米的正方体排成一排,变成一个长方体,表面积减少了6个正方形的面。先求出正方体1个面的面积,再乘6即可。
【详解】1×1×6=6(平方厘米)
所以表面积比原来减少6平方厘米。
故答案为:B
【点睛】解决此题也可用4个正方体表面积的和减去长方体的表面积。
5.B
【分析】如图,两个完全一样的正方体拼成一个长方体后,表面积减少了两个正方形的面,据此分析。
【详解】两个完全一样的正方体拼成一个长方体后,表面积减少了。
故答案为:B
【点睛】两个立体图形(比如正方体之间)拼起来,因为面数目减少,所以表面积减少,但是体积没变。
6.A
【分析】要想最节省包装纸,4个礼品盒组成的长方体表面积最小,把4个礼品盒最大的面重叠在一起,这样最节省包装纸,重叠一次减少2个重叠面的面积,宽和高所在的面面积最小,减少的表面积越多需要的包装纸越少,据此解答。
【详解】A.减少了4个长和宽所在面的面积和4个长和高所在面的面积;
B.减少了4个长和宽所在面的面积和4个宽和高所在面的面积;
C.减少了6个宽和高所在面的面积;
D.减少了4个长和高所在面的面积和4个宽和高所在面的面积。
综上所述,尽可能把礼品盒最大的面重叠在一起,减少的表面积最多,最节省包装纸。
故答案为:A
【点睛】本题主要考查立体图形的切拼,明确减少的面积最多时最节省包装纸是解答题目的关键。
7.A
【分析】正方体的展开图类型:(1)“1—4—1”型:中间4个一连串,两边各一随便放;
(2)“2—3—1”型:二三紧连错一个,三一相连一随便;
(3)“2—2—2”型:两两相连各错一;
(4)“3—3”型:三个两排一对齐;
不能围成正方体的展开图类型:(1)一条线上超过四;(2)“田字形”“七字型”“凹字型”,据此解答。
【详解】A.属于“凹字型”不是正方体的表面展开图;
B.属于“1—4—1”型是正方体的表面展开图;
C.属于“1—4—1”型是正方体的表面展开图;
D.属于“2—2—2”型是正方体的表面展开图。
故答案为:A
【点睛】本题主要考查正方体的展开图,掌握正方体展开图的常见类型是解答题目的关键。
8.B
【分析】由题意可知,如图:若拿走的那块正方体是1号,则表面积比原来减少两个正方形的面积,即1×1×2=2cm2;若拿走的那块正方体是2号,减少了3个正方形的面积,又增加了3个正方形的面积,则表面积不变;若拿走的那块正方体是3号,则表面积比原来增加了2个正方形的面积,即1×1×2=2cm2;若拿走的那块正方体位于后面的中间部分,则表面积比原来增加四个正方形的面积,即1×1×4=4cm2,据此选择即可。
【详解】由分析可知:
所示的物体是由23块棱长为1cm的正方体积木拼搭而成,如果拿走其中的一块,那么剩下物体的表面积与原来相比,不可能减少1cm2。
故答案为:B
【点睛】本题考查表面积,明确表面积的定义是解题的关键。
9.A
【分析】要求长方体水池的占地面积就是求长方体的下底面积,用长方形的面积=长×宽,即可解答。
【详解】由分析可知,长方体水池的占地面积:20×10=200(平方米)
故答案为:A
【点睛】本题考查的目的是理解水池的占地面积,实际求长方体的下底面积。
10.304
【分析】根据长方体表面积的意义,把两个完全一样的小长方体拼成一个大长方体,要使表面积最小也就是把两个小长方体的最大面重合在一起,拼成一个长10厘米,宽8厘米,高(2×2)厘米的长方体,根据长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式解答。
【详解】2×2=4(厘米)
(10×8+10×4+8×4)×2
=(80+40+32)×2
=152×2
=304(平方厘米)
则这个大长方体的表面积最少是304平方厘米。
11. 5 100
【分析】根据正方体棱长总和公式:棱长总和=棱长×12,棱长=棱长总和÷12,代入数据,求出这个正方体的棱长;求四面粘贴彩纸的面积,根据正方形面积公式:面积=棱长×棱长,代入数据,求出一个面的面积,再乘4即可解答。
【详解】60÷12=5(cm)
5×5×4
=25×4
=100(cm2)
焊接一个正方体框架共用去铁丝60cm,这个正方体的棱长是5cm,在这个框架的四面粘贴彩纸,至少需要彩纸是100cm2。
12.(1) 2 4 2
(2)2(n-1)
(3) 22 4n+2
【分析】本题考查的是归纳和总结的能力。
2个相同正方体如图拼在一起,表面积减少2×(2-1)=2个面;
3个相同正方体如图拼在一起,表面积减少2×(3-1)=4个面;
4个相同正方体如图拼在一起,表面积减少2×(4-1)=6个面;
……
由此可归纳出,n个相同正方体如图拼在一起,表面积减少2(n-1)个面。据此解答。
【详解】(1)由图可知,两个正方体拼在一起,有1个“接缝”,2个正方形表面重叠后成为长方体的“内部”,所以表面积减少2个面。三个正方体拼在一起,有2个“接缝”,4个正方形表面重叠后成为长方体的“内部”,所以表面积减少4个面。每增加一个正方体就增加一个接缝,一个接缝就减少2个面。
(2)根据归纳总结可知,n个正方体如图拼在一起,会有(n-1)个接缝,每个接缝处会减少2个面,因此会减少2(n-1)个面。
(3)5个相同正方体如图拼在一起,表面积减少2×(5-1)=8个面。棱长为1厘米,一个面的面积为1平方厘米。由此表面积可列式为:
6×1×5-8×1
=30-8
=22(平方厘米)
n个相同正方体如图拼在一起,表面积减少2(n-1)个面,一个面的面积为1平方厘米。表面积为:
6n×1-2(n-1)×1
=6n-2n+2
=(4n+2)平方厘米
13.×
【分析】正方体展开图有11种特征,分四种类型,即:
第一种:“1﹣4﹣1”结构,即第一行放1个,第二行放4个,第三行放1个;
第二种:“2﹣2﹣2”结构,即每一行放2个正方形,此种结构只有一种展开图;
第三种:“3﹣3”结构,即每一行放3个正方形,只有一种展开图;
第四种:“1﹣3﹣2”结构,即第一行放1个正方形,第二行放3个正方形,第三行放2个正方形。
其中,“田”字型、“L”型和“凹”型不是展开图。据此解答。
【详解】因为这个图形出现了“凹”型,所以不是正方体展开图,不能围成一个正方体。原题说法错误。
故答案为:×
【点睛】充分理解记忆正方体展开图的特征,熟记哪几种情况围不成正方体。
14.√
【分析】根据长方体展开图的类型,主要分为“1-4-l”型,“2-3-1”型, “2-2-2”型,“3-3”型,据此判断解答即可。
【详解】由分析可知:
,属于“1-4-l”型是一个长方体表面展开图。原题说法正确。
故答案为:√
【点睛】本题考查长方体的展开图,明确长方体的展开图的特征是解题的关键。
15.×
【分析】根据长方体、正方体的表面积的意义,长方体的表面积是指长方体的6个面总面积,正方体的表面积是指正方体的6个面的总面积,因此它们表面积的大小跟各自的棱长及长宽高有关,大小并不一定,可举例说明。
【详解】比如长方体的长是3,宽为2,高是1,
长方体的表面积为:
3×2×2+3×1×2+2×1×2
=12+6+4
=22
正方体的棱长是3,则正方体的表面积是3×3×6=54
22<54
可见正方体的表面积并不一定比长方体的表面积小。
故答案为:×
【点睛】此题主要考查正方体、长方体的表面积的意义及计算方法。
16.√
【分析】根据题意可知,长方体一个顶点处切去一个小正方体,表面积减少了3个小正方形的面积,同时又增加了3个小正方形的面积,所以表面积没有变化,据此解答。
【详解】根据分析可知,从一个长方体的顶点处切去一个小正方体后,剩下的物体的表面积不变。原题干说法正确。
故答案为:√
【点睛】本题考查长方体的表面积,明确表面积的意义是解答本题的关键。
17.×
【分析】两个正方体拼成一个长方体后,减少了2个面,据此解答即可。
【详解】两个棱长都是a分米的正方体拼成一个长方体后,减少了2个面,则拼成的这个长方体的表面积是:
6×a2×2-2×a2
=12a2-2a2
=10a2(平方分米)
原题说法错误。
故答案为:×
【点睛】明确两个正方体拼成长方体后减少2个面是解题关键。
18.(1)12平方厘米;(2)8平方厘米;(3)6平方厘米;(4)52平方厘米
【分析】(1)根据上面的面积=长×宽,用4×3即可求出上面的面积;
(2)根据前面的面积=长×高,用4×2即可求出前面的面积;
(3)根据右面的面积=宽×高,用3×2即可求出右面的面积;
(4)根据长方体的特征,可知相对的面积相等,所以用(上面的面积+前面的面积+右面的面积)×2即可求出表面积。
【详解】(1)上面的面积:4×3=12(平方厘米)
(2)前面的面积:4×2=8(平方厘米)
(3)右面的面积:3×2=6(平方厘米)
(4)(12+8+6)×2
=26×2
=52(平方厘米)
这个表面积是52平方厘米。
19.150平方厘米
【分析】正方体的六个面是形状完全相同的正方形,正方体六个面的总面积叫做它的表面积,正方体的表面积=一个面的面积×6,据此解答。
【详解】25×6=150(平方厘米)
所以,图形的表面积是150平方厘米。
20.150;109
【分析】由图可知:在正方体的顶点处去掉一个小长方体,虽然体积减少了,但是表面积不变。根据正方体的表面积公式:S=6a2,体积公式:V=a3,长方体的体积公式:V=abh,把数据分别代入公式解答即可。
【详解】
=25×6
=150()
=25×5
=125()
=8×2
=16()
V:125-16=109()
故立体图形的表面积是150,体积是109。
【点睛】此题主要考查正方体的表面积公式、体积公式、长方体的体积公式的灵活运用,关键是熟记公式。
21.900元
【分析】宫灯分成两部分,上下两个长方体,外饰面的面积等于这两个长方体的侧面积之和,根据长方体的侧面积=底面周长×高,据此求出一个宫灯外饰面的面积,再乘25求出25故宫灯外饰面的面积,最后用外饰面的面积乘每平方米的价格即可解答。
【详解】(66×4×20+46×4×80)×25
=(5280+14720)×25
=20000×25
=500000(平方厘米)
500000平方厘米=50平方米
50×18=900(元)
答:这些宫灯的外饰面一共要花900元。
22.(1)12696平方厘米;(2)不够
【分析】(1)根据正方体表面积=棱长×棱长×6,代入数据解答即可;
(2)正方体棱长和=棱长×12,根据公式计算出需要胶带纸的长度,换算单位后与4.5米比较后判断够不够用即可。
【详解】(1)46×46×6
=2116×6
=12696(平方厘米)
答:至少需要12696平方厘米的红纸。
(2)46×12=552(厘米)
552厘米=5.52米
5.52>4.5
答:一卷4.5米长的胶带纸不够用。
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.如图是一个正方体盒子,下面的图( )是这个正方体盒子的展开图。
A. B. C. D.
2.“仁、义、礼、智、信、孝”是我国的传统美德,小明将这六个字分别写在一个正方体的六个面上,下图是这个正方体的平面展开图,在这个正方体中,和“礼”相对的字是( )。
A.“仁” B.“智” C.“信” D.“孝”
3.把一个长6分米,宽5分米,高3分米的长方体切成两个同样的小长方体,表面积最多增加( )平方分米。
A.90 B.30 C.36 D.60
4.把4个棱长1厘米的正方体排成一排,变成一个长方体,表面积比原来减少( )平方厘米。
A.4 B.6 C.8 D.3
5.两个一样的正方体,拼成一个长方体,表面积( )。
A.增加了 B.减少了 C.不变 D.无法确定
6.如果把4个礼品盒包装在一起,下面几种方法中,最节省包装纸的是( )。
A. B.
C. D.
7.下面四个图形中,不是正方体表面展开图的是( )。
A. B.
C. D.
8.如图所示的物体是由23块棱长为1cm的正方体积木拼搭而成,如果拿走其中的一块,那么剩下物体的表面积与原来相比,不可能是( )。
A.不变的 B.减少 C.减少 D.增加
9.一个长方体水池,长20米,宽10米,深2米,占地( )平方米。
A.200 B.400 C.520
二、填空题
10.把两个长、宽、高分别是10厘米、8厘米、2厘米的相同长方体拼成一个大长方体,这个大长方体的表面积最少是( )平方厘米。
11.焊接一个正方体框架共用去铁丝60cm,这个正方体的棱长是( )cm,在这个框架的四面粘贴彩纸,至少需要彩纸是( )cm2。
12.如图:
(1)两个完全相同的正方体拼在一起,表面积减少( )个面,三个正方体拼在一起减少( )个面;每增加一个正方体减少( )面。
(2)n个小正方体拼在一起减少( )面。
(3)如果小正方体的棱长是1厘米,5个小正方体如上图一样拼在一起表面积是( )平方厘米,n个小正方体拼在一起表面积是( )平方厘米。
三、判断题
13.这个图形能围成一个正方体。( )
14.下面是一个长方体表面展开图。( )
15.正方体的表面积比长方体的表面积小。( )
16.从一个长方体的顶点处切下一个小正方体后,剩下的物体的表面积不变。( )
17.把两个棱长都是a分米的正方体拼成一个长方体,拼成的这个长方体的表面积是12a2平方分米。( )
四、计算题
18.求下面图形的表面积。
(1)上面的面积:
(2)前面的面积:
(3)右面的面积:
(4)长方体的表面积:
19.求出下面正方体的表面积。
20.计算下面立体图形的表面积和体积。(单位:dm)
五、解答题
21.某古建筑景点定做了25个宫灯(如图,单位:厘米)。宫灯外侧有一层外饰面(上、下面除外)。如果外饰面每平方米18元,这些宫灯的外饰面一共要花多少钱?
22.把一个棱长46厘米的正方体纸箱各面都贴上红纸,作为捐款箱。
(1)至少需要多少平方厘米的红纸?(开口处忽略不计。)
(2)如果只在棱上粘贴一圈胶带纸,一卷4.5米长的胶带纸够用吗?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】正方体的6个面是完全相同的正方形,正方体中相对的两个面不相邻,题中的正方体、、所在的面是相邻的三个面,据此解答。
【详解】A.和所在的两个面是相对面,不符合题意;
B.、、所在的三个面相邻,但是正方体中所在的面和的一条直角边所在的棱重合,不符合题意;
C.和所在的两个面是相对面,不符合题意;
D.以所在的面为顶面可以折成正方体,符合题意。
故答案为:D
【点睛】本题主要考查正方体的展开图,掌握正方体的特征并想象展开图折成后的正方体是解答题目的关键。
2.C
【分析】“2—3—1”型的正方体找相对面时,先找同行,同行中间隔1个正方形的是相对面,再找异行,异行中间隔2个正方形的是相对面,据此解答。
【详解】分析可知,“礼”和“信”是相对面,“仁”和“智”是相对面,“义”和“孝”是相对面。
故答案为:C
【点睛】掌握正方体的展开图找相对面的方法是解答题目的关键。
3.D
【分析】切割一次增加两个切割面的面积,切割面越大则增加的面积越多,分别计算长乘宽、长乘高以及宽乘高的面分别是多大,选最大的面作为切割面,据此分析求解。
【详解】5×6=30(平方分米)
3×6=18(平方分米)
3×5=15(平方分米)
30>18>15
30×2=60(平方分米)
表面积最多增加60平方分米。
故答案为:D
【点睛】明确切割一次增加两个面是解题的关键。
4.B
【分析】如下图:把4个棱长1厘米的正方体排成一排,变成一个长方体,表面积减少了6个正方形的面。先求出正方体1个面的面积,再乘6即可。
【详解】1×1×6=6(平方厘米)
所以表面积比原来减少6平方厘米。
故答案为:B
【点睛】解决此题也可用4个正方体表面积的和减去长方体的表面积。
5.B
【分析】如图,两个完全一样的正方体拼成一个长方体后,表面积减少了两个正方形的面,据此分析。
【详解】两个完全一样的正方体拼成一个长方体后,表面积减少了。
故答案为:B
【点睛】两个立体图形(比如正方体之间)拼起来,因为面数目减少,所以表面积减少,但是体积没变。
6.A
【分析】要想最节省包装纸,4个礼品盒组成的长方体表面积最小,把4个礼品盒最大的面重叠在一起,这样最节省包装纸,重叠一次减少2个重叠面的面积,宽和高所在的面面积最小,减少的表面积越多需要的包装纸越少,据此解答。
【详解】A.减少了4个长和宽所在面的面积和4个长和高所在面的面积;
B.减少了4个长和宽所在面的面积和4个宽和高所在面的面积;
C.减少了6个宽和高所在面的面积;
D.减少了4个长和高所在面的面积和4个宽和高所在面的面积。
综上所述,尽可能把礼品盒最大的面重叠在一起,减少的表面积最多,最节省包装纸。
故答案为:A
【点睛】本题主要考查立体图形的切拼,明确减少的面积最多时最节省包装纸是解答题目的关键。
7.A
【分析】正方体的展开图类型:(1)“1—4—1”型:中间4个一连串,两边各一随便放;
(2)“2—3—1”型:二三紧连错一个,三一相连一随便;
(3)“2—2—2”型:两两相连各错一;
(4)“3—3”型:三个两排一对齐;
不能围成正方体的展开图类型:(1)一条线上超过四;(2)“田字形”“七字型”“凹字型”,据此解答。
【详解】A.属于“凹字型”不是正方体的表面展开图;
B.属于“1—4—1”型是正方体的表面展开图;
C.属于“1—4—1”型是正方体的表面展开图;
D.属于“2—2—2”型是正方体的表面展开图。
故答案为:A
【点睛】本题主要考查正方体的展开图,掌握正方体展开图的常见类型是解答题目的关键。
8.B
【分析】由题意可知,如图:若拿走的那块正方体是1号,则表面积比原来减少两个正方形的面积,即1×1×2=2cm2;若拿走的那块正方体是2号,减少了3个正方形的面积,又增加了3个正方形的面积,则表面积不变;若拿走的那块正方体是3号,则表面积比原来增加了2个正方形的面积,即1×1×2=2cm2;若拿走的那块正方体位于后面的中间部分,则表面积比原来增加四个正方形的面积,即1×1×4=4cm2,据此选择即可。
【详解】由分析可知:
所示的物体是由23块棱长为1cm的正方体积木拼搭而成,如果拿走其中的一块,那么剩下物体的表面积与原来相比,不可能减少1cm2。
故答案为:B
【点睛】本题考查表面积,明确表面积的定义是解题的关键。
9.A
【分析】要求长方体水池的占地面积就是求长方体的下底面积,用长方形的面积=长×宽,即可解答。
【详解】由分析可知,长方体水池的占地面积:20×10=200(平方米)
故答案为:A
【点睛】本题考查的目的是理解水池的占地面积,实际求长方体的下底面积。
10.304
【分析】根据长方体表面积的意义,把两个完全一样的小长方体拼成一个大长方体,要使表面积最小也就是把两个小长方体的最大面重合在一起,拼成一个长10厘米,宽8厘米,高(2×2)厘米的长方体,根据长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式解答。
【详解】2×2=4(厘米)
(10×8+10×4+8×4)×2
=(80+40+32)×2
=152×2
=304(平方厘米)
则这个大长方体的表面积最少是304平方厘米。
11. 5 100
【分析】根据正方体棱长总和公式:棱长总和=棱长×12,棱长=棱长总和÷12,代入数据,求出这个正方体的棱长;求四面粘贴彩纸的面积,根据正方形面积公式:面积=棱长×棱长,代入数据,求出一个面的面积,再乘4即可解答。
【详解】60÷12=5(cm)
5×5×4
=25×4
=100(cm2)
焊接一个正方体框架共用去铁丝60cm,这个正方体的棱长是5cm,在这个框架的四面粘贴彩纸,至少需要彩纸是100cm2。
12.(1) 2 4 2
(2)2(n-1)
(3) 22 4n+2
【分析】本题考查的是归纳和总结的能力。
2个相同正方体如图拼在一起,表面积减少2×(2-1)=2个面;
3个相同正方体如图拼在一起,表面积减少2×(3-1)=4个面;
4个相同正方体如图拼在一起,表面积减少2×(4-1)=6个面;
……
由此可归纳出,n个相同正方体如图拼在一起,表面积减少2(n-1)个面。据此解答。
【详解】(1)由图可知,两个正方体拼在一起,有1个“接缝”,2个正方形表面重叠后成为长方体的“内部”,所以表面积减少2个面。三个正方体拼在一起,有2个“接缝”,4个正方形表面重叠后成为长方体的“内部”,所以表面积减少4个面。每增加一个正方体就增加一个接缝,一个接缝就减少2个面。
(2)根据归纳总结可知,n个正方体如图拼在一起,会有(n-1)个接缝,每个接缝处会减少2个面,因此会减少2(n-1)个面。
(3)5个相同正方体如图拼在一起,表面积减少2×(5-1)=8个面。棱长为1厘米,一个面的面积为1平方厘米。由此表面积可列式为:
6×1×5-8×1
=30-8
=22(平方厘米)
n个相同正方体如图拼在一起,表面积减少2(n-1)个面,一个面的面积为1平方厘米。表面积为:
6n×1-2(n-1)×1
=6n-2n+2
=(4n+2)平方厘米
13.×
【分析】正方体展开图有11种特征,分四种类型,即:
第一种:“1﹣4﹣1”结构,即第一行放1个,第二行放4个,第三行放1个;
第二种:“2﹣2﹣2”结构,即每一行放2个正方形,此种结构只有一种展开图;
第三种:“3﹣3”结构,即每一行放3个正方形,只有一种展开图;
第四种:“1﹣3﹣2”结构,即第一行放1个正方形,第二行放3个正方形,第三行放2个正方形。
其中,“田”字型、“L”型和“凹”型不是展开图。据此解答。
【详解】因为这个图形出现了“凹”型,所以不是正方体展开图,不能围成一个正方体。原题说法错误。
故答案为:×
【点睛】充分理解记忆正方体展开图的特征,熟记哪几种情况围不成正方体。
14.√
【分析】根据长方体展开图的类型,主要分为“1-4-l”型,“2-3-1”型, “2-2-2”型,“3-3”型,据此判断解答即可。
【详解】由分析可知:
,属于“1-4-l”型是一个长方体表面展开图。原题说法正确。
故答案为:√
【点睛】本题考查长方体的展开图,明确长方体的展开图的特征是解题的关键。
15.×
【分析】根据长方体、正方体的表面积的意义,长方体的表面积是指长方体的6个面总面积,正方体的表面积是指正方体的6个面的总面积,因此它们表面积的大小跟各自的棱长及长宽高有关,大小并不一定,可举例说明。
【详解】比如长方体的长是3,宽为2,高是1,
长方体的表面积为:
3×2×2+3×1×2+2×1×2
=12+6+4
=22
正方体的棱长是3,则正方体的表面积是3×3×6=54
22<54
可见正方体的表面积并不一定比长方体的表面积小。
故答案为:×
【点睛】此题主要考查正方体、长方体的表面积的意义及计算方法。
16.√
【分析】根据题意可知,长方体一个顶点处切去一个小正方体,表面积减少了3个小正方形的面积,同时又增加了3个小正方形的面积,所以表面积没有变化,据此解答。
【详解】根据分析可知,从一个长方体的顶点处切去一个小正方体后,剩下的物体的表面积不变。原题干说法正确。
故答案为:√
【点睛】本题考查长方体的表面积,明确表面积的意义是解答本题的关键。
17.×
【分析】两个正方体拼成一个长方体后,减少了2个面,据此解答即可。
【详解】两个棱长都是a分米的正方体拼成一个长方体后,减少了2个面,则拼成的这个长方体的表面积是:
6×a2×2-2×a2
=12a2-2a2
=10a2(平方分米)
原题说法错误。
故答案为:×
【点睛】明确两个正方体拼成长方体后减少2个面是解题关键。
18.(1)12平方厘米;(2)8平方厘米;(3)6平方厘米;(4)52平方厘米
【分析】(1)根据上面的面积=长×宽,用4×3即可求出上面的面积;
(2)根据前面的面积=长×高,用4×2即可求出前面的面积;
(3)根据右面的面积=宽×高,用3×2即可求出右面的面积;
(4)根据长方体的特征,可知相对的面积相等,所以用(上面的面积+前面的面积+右面的面积)×2即可求出表面积。
【详解】(1)上面的面积:4×3=12(平方厘米)
(2)前面的面积:4×2=8(平方厘米)
(3)右面的面积:3×2=6(平方厘米)
(4)(12+8+6)×2
=26×2
=52(平方厘米)
这个表面积是52平方厘米。
19.150平方厘米
【分析】正方体的六个面是形状完全相同的正方形,正方体六个面的总面积叫做它的表面积,正方体的表面积=一个面的面积×6,据此解答。
【详解】25×6=150(平方厘米)
所以,图形的表面积是150平方厘米。
20.150;109
【分析】由图可知:在正方体的顶点处去掉一个小长方体,虽然体积减少了,但是表面积不变。根据正方体的表面积公式:S=6a2,体积公式:V=a3,长方体的体积公式:V=abh,把数据分别代入公式解答即可。
【详解】
=25×6
=150()
=25×5
=125()
=8×2
=16()
V:125-16=109()
故立体图形的表面积是150,体积是109。
【点睛】此题主要考查正方体的表面积公式、体积公式、长方体的体积公式的灵活运用,关键是熟记公式。
21.900元
【分析】宫灯分成两部分,上下两个长方体,外饰面的面积等于这两个长方体的侧面积之和,根据长方体的侧面积=底面周长×高,据此求出一个宫灯外饰面的面积,再乘25求出25故宫灯外饰面的面积,最后用外饰面的面积乘每平方米的价格即可解答。
【详解】(66×4×20+46×4×80)×25
=(5280+14720)×25
=20000×25
=500000(平方厘米)
500000平方厘米=50平方米
50×18=900(元)
答:这些宫灯的外饰面一共要花900元。
22.(1)12696平方厘米;(2)不够
【分析】(1)根据正方体表面积=棱长×棱长×6,代入数据解答即可;
(2)正方体棱长和=棱长×12,根据公式计算出需要胶带纸的长度,换算单位后与4.5米比较后判断够不够用即可。
【详解】(1)46×46×6
=2116×6
=12696(平方厘米)
答:至少需要12696平方厘米的红纸。
(2)46×12=552(厘米)
552厘米=5.52米
5.52>4.5
答:一卷4.5米长的胶带纸不够用。
答案第1页,共2页
答案第1页,共2页
