数学人教A版(2019)必修第二册6.4.3正弦定理 课件(共26张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第二册6.4.3正弦定理 课件(共26张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-10 14:10:38 | ||
图片预览


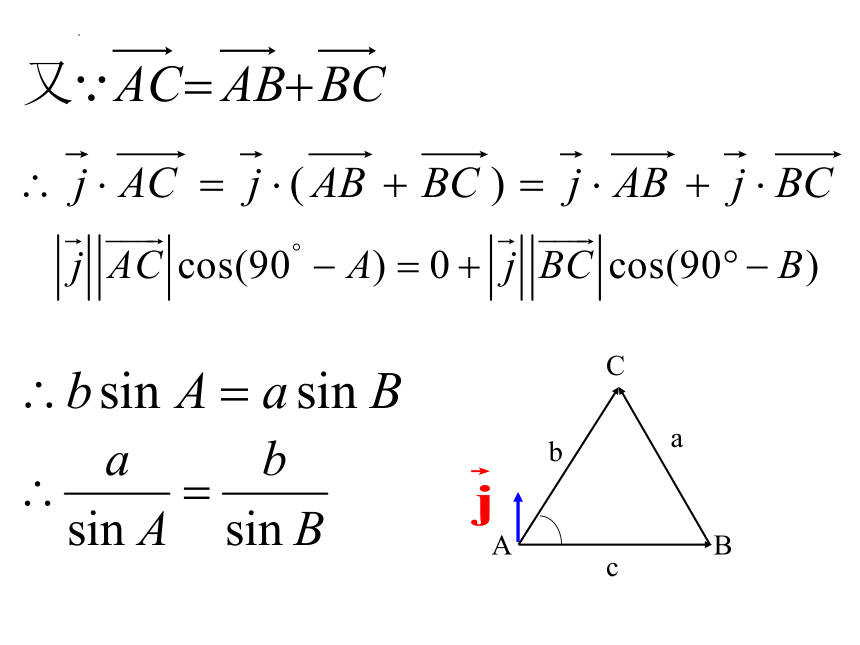
文档简介
(共26张PPT)
6.4.3正弦定理
学习目标
1、通过对任意三角形边长和角度关系的探索,掌握正弦定理,并能解决一些简单的问题;
2、通过对特殊三角形边角间数量关系的研究,发现正弦定理,初步学会运用由特殊到一般的思想方法发现数学规律;
3、通过参与、思考、交流,体验正弦定理的发现过程,逐步培养探索精神和创新意识;通过对正弦函数的学习体会数学的对称美,和谐美.
复习三角形中的边角关系
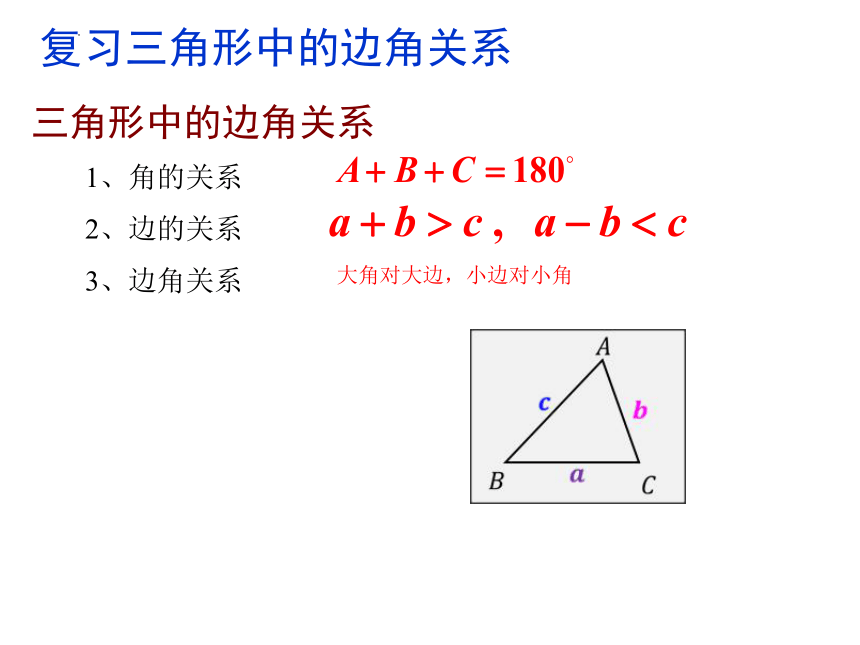
1、角的关系
2、边的关系
3、边角关系
大角对大边,小边对小角
三角形中的边角关系
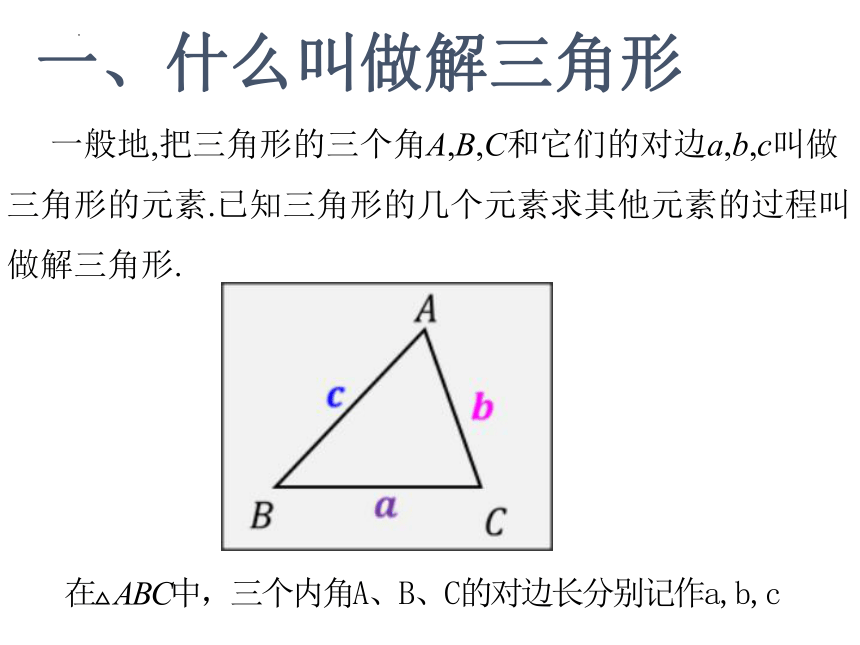
一般地,把三角形的三个角A,B,C和它们的对边a,b,c叫做三角形的元素.已知三角形的几个元素求其他元素的过程叫做解三角形.
一、什么叫做解三角形
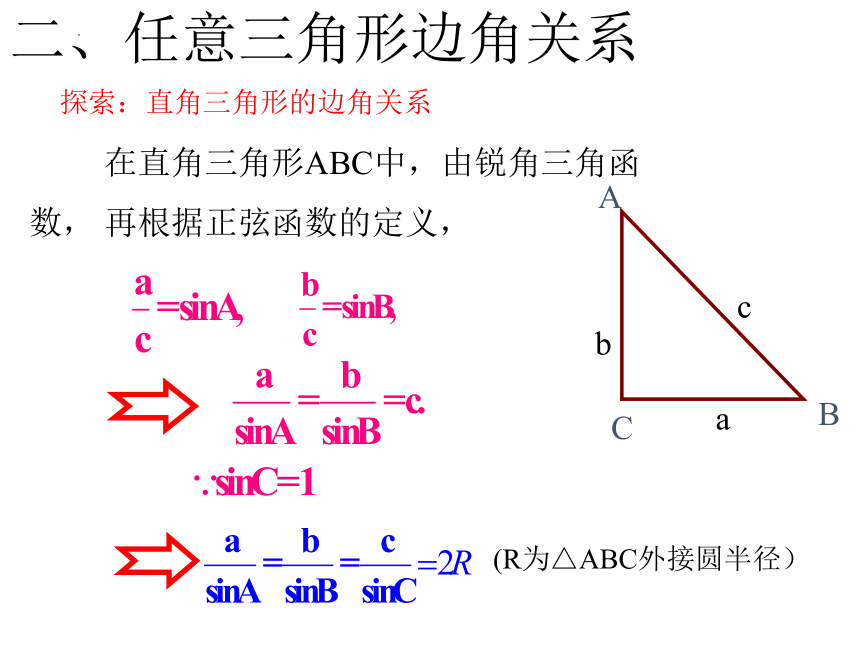
探索:直角三角形的边角关系
二、任意三角形边角关系
在直角三角形ABC中,由锐角三角函数, 再根据正弦函数的定义,
A
B
C
a
b
c
(R为△ABC外接圆半径)
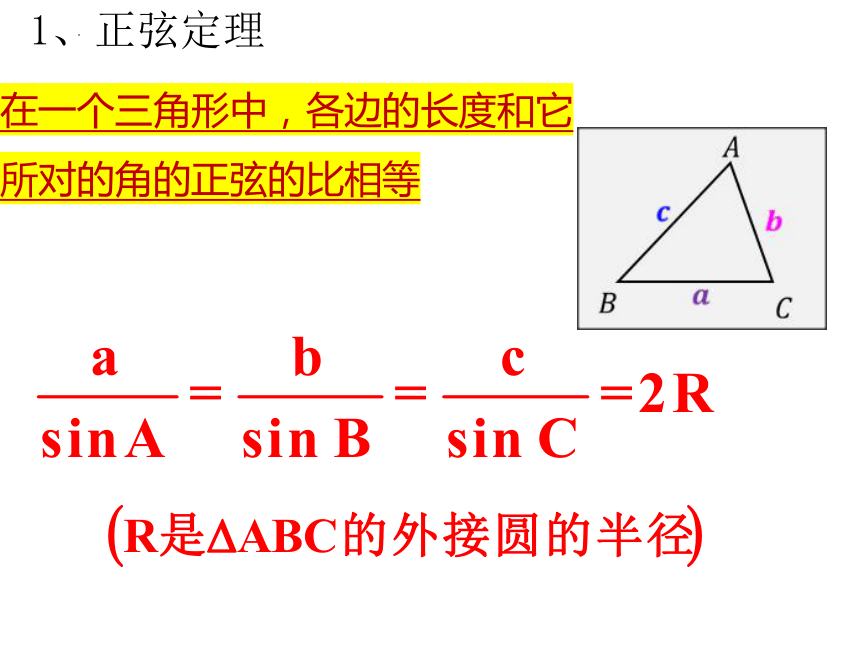
1、正弦定理
在一个三角形中,各边的长度和它所对的角的正弦的比相等
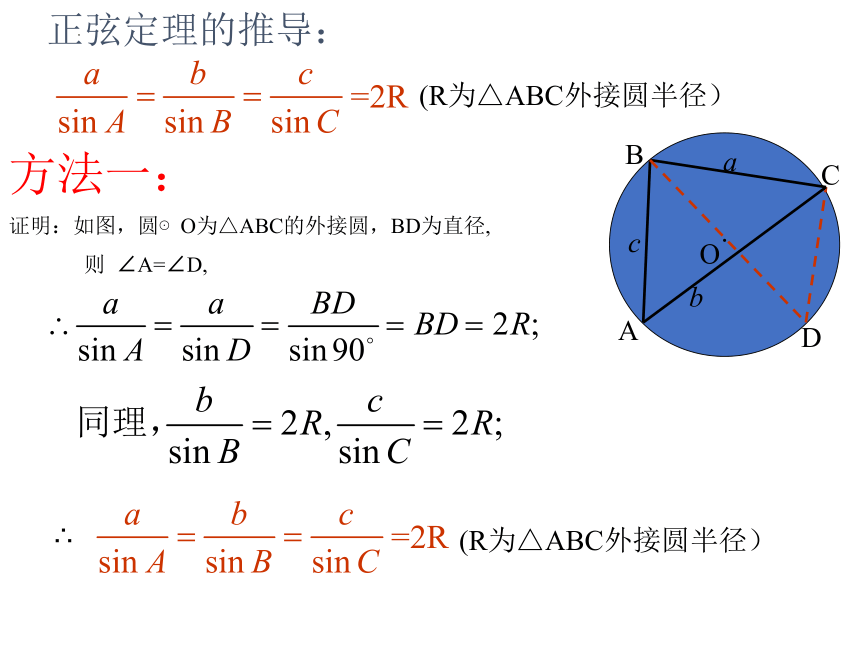
正弦定理的推导:
A
B
D
C
.
O
b
a
c
=2R
(R为△ABC外接圆半径)
证明:如图,圆⊙O为△ABC的外接圆,BD为直径,
则 ∠A=∠D,
∴
=2R
(R为△ABC外接圆半径)
方法一:
证明:
B
A
C
a
c
b
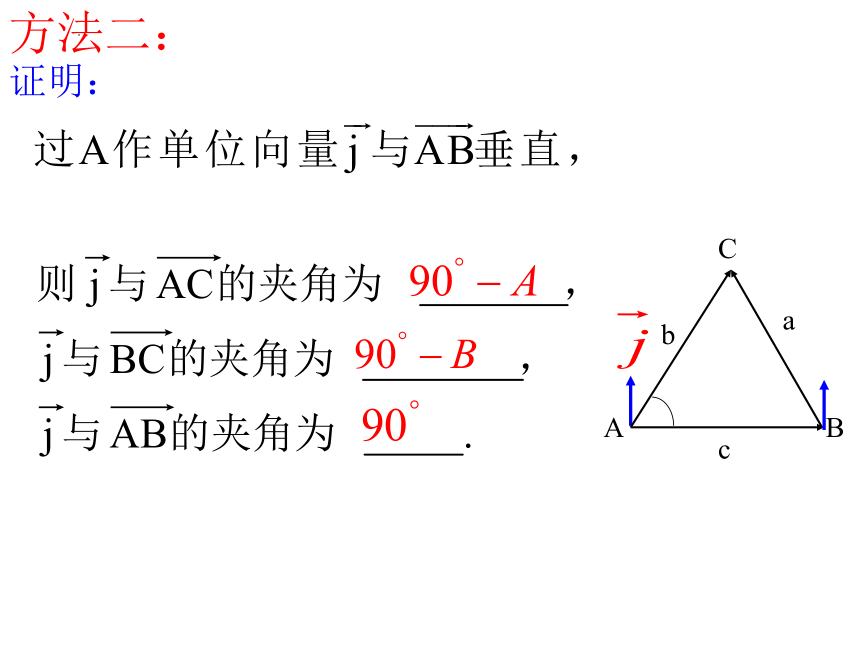
方法二:
B
A
C
a
c
b
A
B
C
类似可推出,三角形为钝角三角形时,以上关系式仍然成立.
方法三:
1.公式变形式:
(1)a=2RsinA,b=2RsinB,c=2RsinC(边化角公式)
(3)a:b:c=sinA:sinB:sinC
利用正弦定理可以实现边角互化,可以解决以下
三、正弦定理解决两类问题:
1、已知两角和任一边,求其它两边和一角。AAS
2、已知两边和其中一边的对角,求另一边的对角。 SSA
(从而进一步求出其他的边和角,包括解的个数的讨论问题)
题型一已知两角一边,求其它元素.
例1、在△ABC中,已知
A=45
C=30 ,求b
0
0
0
0
0
105
)
30
45
(
180
)
(
180
=
+
-
=
+
-
=
C
A
B
解:
由正弦定理 得:
例2、在△ABC中,已知a=16, b= ,
A=30°,求角B,C和边c.
解:由正弦定理
得
所以
B=60°,
或B=120°
当 时
B=60°
C=90°
C=30°
当B=120°时
题型二已知两边及其中一边的对角,求其它元素.
∵b>a,∴B>A=45o,∴有两解B=60o或120o
1)当B=60o时,C=75o,
2)当B=120o时,C=15o,
作业
在△ABC中,已知a,b和A,以点C为圆心,边长a为半径画弧,此弧与除去顶点A的射线AB的公共点的个数即为三角形的个数.
三角形解的个数的确定
1.判断正误,正确的画“√”,错误的画“ ”.
1.正弦定理适用于任意三角形. ( √ )
2.在△ABC中,必有asin C=csin A. ( √ )
提示:由 = ,得asin C=csin A.
3.在△ABC 中,一定有 a∶b∶c = sin A∶sin B∶sin C. ( √ )
4.在△ABC中,a>b A>B sin A>sin B. ( √ )
5.在△ABC中,若sin 2A=sin 2B,则必有A=B. ( )
基础练习
2.判断题:根据已知条件判断△ABC解的情况.
(1) b=1 ,a=2,A=30o 有一解; .
(2)b=1, a=3,B=30o 无解; .
(3)b=1,a= ,A=30o 有一解; .
(4)b=1,a= ,B=150o 有一解; .
(5)b= ,a=1,B=120o有两解. .
3
3
3
练习
C
2.在△ABC中,若a=18,b=24,A=45°,则此三角形有( )
A.无解 B.两解 C.一解 D.解的个数不确定
B
B
C
3或6
形状。
所以三角形ABC是等腰三角形或直角三角形。
为锐角,试判断此三角形的形状。
10、在△ABC中,如果lga-lgc=lgsinB=-lg ,且B
所以此三角形为等腰直角三角形
2.正弦定理的外在形式是公式,它由三个等式组成即
, ,
每个等式都表示三角形的两个角和它们的对边的关系.
1.三角形的三个内角及其对边叫做三角形的元素,已知三角形的几个元素求其他元素的过程叫做解三角形.
课堂小结
3.利用正弦定理可以解决两类解三角形的问题:一类是已知两角和一边解三角形;另一类是已知两边和其中一边的对角解三角形.对于第二类问题,要注意确定解的个数.
课堂小结
6.4.3正弦定理
学习目标
1、通过对任意三角形边长和角度关系的探索,掌握正弦定理,并能解决一些简单的问题;
2、通过对特殊三角形边角间数量关系的研究,发现正弦定理,初步学会运用由特殊到一般的思想方法发现数学规律;
3、通过参与、思考、交流,体验正弦定理的发现过程,逐步培养探索精神和创新意识;通过对正弦函数的学习体会数学的对称美,和谐美.
复习三角形中的边角关系
1、角的关系
2、边的关系
3、边角关系
大角对大边,小边对小角
三角形中的边角关系
一般地,把三角形的三个角A,B,C和它们的对边a,b,c叫做三角形的元素.已知三角形的几个元素求其他元素的过程叫做解三角形.
一、什么叫做解三角形
探索:直角三角形的边角关系
二、任意三角形边角关系
在直角三角形ABC中,由锐角三角函数, 再根据正弦函数的定义,
A
B
C
a
b
c
(R为△ABC外接圆半径)
1、正弦定理
在一个三角形中,各边的长度和它所对的角的正弦的比相等
正弦定理的推导:
A
B
D
C
.
O
b
a
c
=2R
(R为△ABC外接圆半径)
证明:如图,圆⊙O为△ABC的外接圆,BD为直径,
则 ∠A=∠D,
∴
=2R
(R为△ABC外接圆半径)
方法一:
证明:
B
A
C
a
c
b
方法二:
B
A
C
a
c
b
A
B
C
类似可推出,三角形为钝角三角形时,以上关系式仍然成立.
方法三:
1.公式变形式:
(1)a=2RsinA,b=2RsinB,c=2RsinC(边化角公式)
(3)a:b:c=sinA:sinB:sinC
利用正弦定理可以实现边角互化,可以解决以下
三、正弦定理解决两类问题:
1、已知两角和任一边,求其它两边和一角。AAS
2、已知两边和其中一边的对角,求另一边的对角。 SSA
(从而进一步求出其他的边和角,包括解的个数的讨论问题)
题型一已知两角一边,求其它元素.
例1、在△ABC中,已知
A=45
C=30 ,求b
0
0
0
0
0
105
)
30
45
(
180
)
(
180
=
+
-
=
+
-
=
C
A
B
解:
由正弦定理 得:
例2、在△ABC中,已知a=16, b= ,
A=30°,求角B,C和边c.
解:由正弦定理
得
所以
B=60°,
或B=120°
当 时
B=60°
C=90°
C=30°
当B=120°时
题型二已知两边及其中一边的对角,求其它元素.
∵b>a,∴B>A=45o,∴有两解B=60o或120o
1)当B=60o时,C=75o,
2)当B=120o时,C=15o,
作业
在△ABC中,已知a,b和A,以点C为圆心,边长a为半径画弧,此弧与除去顶点A的射线AB的公共点的个数即为三角形的个数.
三角形解的个数的确定
1.判断正误,正确的画“√”,错误的画“ ”.
1.正弦定理适用于任意三角形. ( √ )
2.在△ABC中,必有asin C=csin A. ( √ )
提示:由 = ,得asin C=csin A.
3.在△ABC 中,一定有 a∶b∶c = sin A∶sin B∶sin C. ( √ )
4.在△ABC中,a>b A>B sin A>sin B. ( √ )
5.在△ABC中,若sin 2A=sin 2B,则必有A=B. ( )
基础练习
2.判断题:根据已知条件判断△ABC解的情况.
(1) b=1 ,a=2,A=30o 有一解; .
(2)b=1, a=3,B=30o 无解; .
(3)b=1,a= ,A=30o 有一解; .
(4)b=1,a= ,B=150o 有一解; .
(5)b= ,a=1,B=120o有两解. .
3
3
3
练习
C
2.在△ABC中,若a=18,b=24,A=45°,则此三角形有( )
A.无解 B.两解 C.一解 D.解的个数不确定
B
B
C
3或6
形状。
所以三角形ABC是等腰三角形或直角三角形。
为锐角,试判断此三角形的形状。
10、在△ABC中,如果lga-lgc=lgsinB=-lg ,且B
所以此三角形为等腰直角三角形
2.正弦定理的外在形式是公式,它由三个等式组成即
, ,
每个等式都表示三角形的两个角和它们的对边的关系.
1.三角形的三个内角及其对边叫做三角形的元素,已知三角形的几个元素求其他元素的过程叫做解三角形.
课堂小结
3.利用正弦定理可以解决两类解三角形的问题:一类是已知两角和一边解三角形;另一类是已知两边和其中一边的对角解三角形.对于第二类问题,要注意确定解的个数.
课堂小结
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
