5.1相交线 练习(含答案)2023-2024学年人教版七年级数学下册
文档属性
| 名称 | 5.1相交线 练习(含答案)2023-2024学年人教版七年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 166.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-10 12:53:07 | ||
图片预览


文档简介
5.1相交线 练习2023-2024学年人教版七年级数学下册
一.选择题(共12小题)
1.下列各图中,∠1与∠2互为对顶角的是( )
A. B. C. D.
2.如图,三条直线a、b、c相交于一点,则∠1+∠2+∠3等于( )
A.180° B.120° C.90° D.不能确定
3.已知图①~④,
在上述四个图中,∠1与∠2是同位角的有( )
A.①②③④ B.①②③ C.①③ D.①
4.如图所示,已知直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COB,∠BOE=36°,则∠AOF的度数为( )
A.54° B.126° C.36° D.90°
5.如图,属于同位角的是( )
A.∠1和∠2 B.∠1和∠3 C.∠1和∠4 D.∠2和∠3
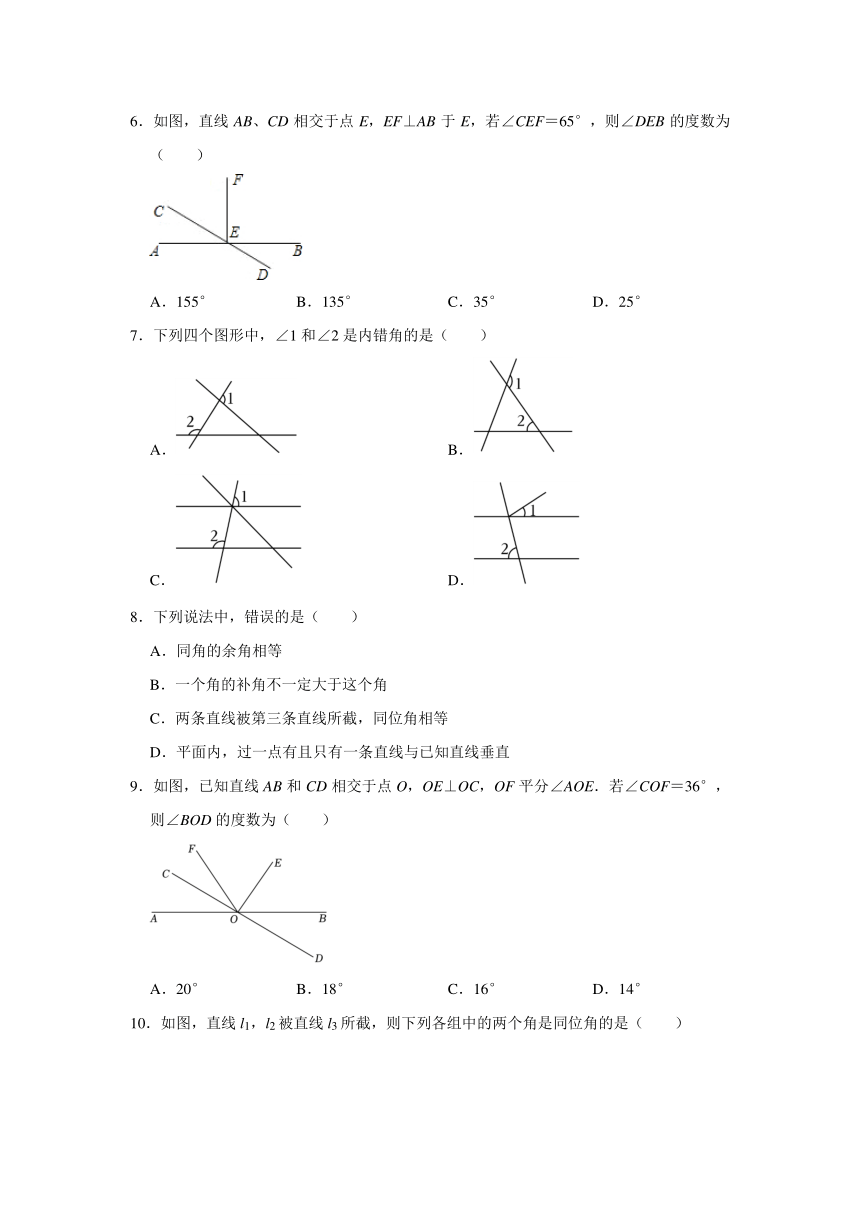
6.如图,直线AB、CD相交于点E,EF⊥AB于E,若∠CEF=65°,则∠DEB的度数为( )
A.155° B.135° C.35° D.25°
7.下列四个图形中,∠1和∠2是内错角的是( )
A. B.
C. D.
8.下列说法中,错误的是( )
A.同角的余角相等
B.一个角的补角不一定大于这个角
C.两条直线被第三条直线所截,同位角相等
D.平面内,过一点有且只有一条直线与已知直线垂直
9.如图,已知直线AB和CD相交于点O,OE⊥OC,OF平分∠AOE.若∠COF=36°,则∠BOD的度数为( )
A.20° B.18° C.16° D.14°
10.如图,直线l1,l2被直线l3所截,则下列各组中的两个角是同位角的是( )
A.∠3与∠4 B.∠2与∠4 C.∠1与∠3 D.∠1与∠2
11.如图,点O在直线AB上,OC⊥OD,若∠AOC=150°,则∠BOD的大小为( )
A.30° B.40° C.50° D.60°
12.若点A到直线l的距离为7cm,点B到直线l的距离为3cm,则线段AB的长度为( )
A.10cm B.4cm C.10cm或4cm D.至少4cm
二.填空题(共5小题)
13.如图,在灌溉时,要把河中的水引到农田P处,农民李伯伯的做法是:过点P作PM垂直于河岸l,垂足为M,沿PM开挖水渠距离最短,其中的数学道理是 .
14.在直角三角形ABC中,∠ACB=90°,AC=6,BC=8,AB=10,则点C到AB的距离为 .
15.如图,直线AB、CD相交于点O,OE平分∠BOD,若∠AOD=100°,则∠BOE= .
16.如图,直线AB,CD相交于点O,EO⊥CD.若∠AOE=2∠AOC,则∠BOD的度数为 °.
17.已知∠1和∠2互为邻补角,若∠1=80°,则∠2=
三.解答题(共5小题)
18.如图,直线AB、CD交于点O,OP⊥CD于点O,如果OA平分∠POD,求∠BOC的度数.
19.如图,直线AB,CD相交于点O.已知,∠EOC:∠EOD=4:5,OA平分∠EOC,求∠AOC的度数.
20.平面内两条直线EF、CD相交于点O,OA⊥OB,OC恰好平分∠AOF.
(1)如图1,若∠AOE=40°,求∠BOD的度数;
(2)在图1中,若∠AOE=x°,请求出∠BOD的度数(用含有x的式子表示),并写出∠AOE和∠BOD的数量关系;
(3)如图2,当OA,OB在直线EF的同侧时,∠AOE和∠BOD的数量关系是否会发生改变?若不变,请直接写出它们之间的数量关系;若发生变化,请说明理由.
21.如图,直线AB、CD相交于点O,OM⊥AB.
(1)若∠1=∠2,证明:ON⊥CD;
(2)若∠1=∠BOC,求∠BOD的度数.
22.如图,直线AB,CD相交于点O,OE⊥AB,垂足为O.
(1)直接写出图中∠AOC的对顶角为 ,∠BOD的邻补角为 ;
(2)若∠BOD:∠COE=1:2,求∠AOD的度数.
参考答案
一.选择题(共12小题)
1--10BACBC DBCBB 11--12DD
二.填空题(共5小题)
13.垂线段最短.
14.4.8.
15.40°.
16.30.
17.100°.
三.解答题(共5小题)
18.解:∵OP⊥CD,
∴∠DOP=90°,
又∵OA平分∠POD,
∴∠AOD=∠POD=45°,
∴∠BOC=∠AOD=45°.
19.解:∵∠EOC:∠EOD=4:5,∠EOC+∠EOD=180°,
∴∠EOC=×180°=80°,
∵OA平分∠EOC,
∴∠AOC=∠AOE=∠EOC=40°.
20.解:(1)∵∠AOE=40°,
∴∠AOF=180°﹣∠AOE=140°,
∵OC平分∠AOF,
∴,
∵OA⊥OB,
∴∠AOB=90°,
∴∠BOD=180°﹣∠AOB﹣∠AOC=20°;
(2)∵∠AOE=x°,
∴∠AOF=180°﹣∠AOE=(180﹣x)°,
∵OC平分∠AOF,
∴,
∵OA⊥OB,
∴∠AOB=90°,
∴;
∴∠AOE=2∠BOD;
(3)不变,∠AOE=2∠BOD.
21.证明:(1)∵OM⊥AB,
∴∠AOM=∠BOM=90°,
∴∠1+∠AOC=90°,
∵∠1=∠2,
∴∠2+∠AOC=90°,
即∠CON=90°,
∴ON⊥CD;
(2)∵∠1=∠BOC,
∴∠BOM=2∠1=90°,
解得:∠1=45°,
∴∠BOD=90°﹣45°=45°
22.解:(1)∠AOC的对顶角为∠BOD,∠BOD的邻补角为∠AOD,∠BOC,
(2)∵OE⊥AB,
∴∠AOE=90°,
∴∠AOC+∠COE=90°,
∵∠BOD=∠AOC,
∵∠BOD:∠COE=1:2,
∴∠BOD=30°,
∴∠AOD=150°,
故答案为:∠BOD;∠AOD,∠BOC
一.选择题(共12小题)
1.下列各图中,∠1与∠2互为对顶角的是( )
A. B. C. D.
2.如图,三条直线a、b、c相交于一点,则∠1+∠2+∠3等于( )
A.180° B.120° C.90° D.不能确定
3.已知图①~④,
在上述四个图中,∠1与∠2是同位角的有( )
A.①②③④ B.①②③ C.①③ D.①
4.如图所示,已知直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COB,∠BOE=36°,则∠AOF的度数为( )
A.54° B.126° C.36° D.90°
5.如图,属于同位角的是( )
A.∠1和∠2 B.∠1和∠3 C.∠1和∠4 D.∠2和∠3
6.如图,直线AB、CD相交于点E,EF⊥AB于E,若∠CEF=65°,则∠DEB的度数为( )
A.155° B.135° C.35° D.25°
7.下列四个图形中,∠1和∠2是内错角的是( )
A. B.
C. D.
8.下列说法中,错误的是( )
A.同角的余角相等
B.一个角的补角不一定大于这个角
C.两条直线被第三条直线所截,同位角相等
D.平面内,过一点有且只有一条直线与已知直线垂直
9.如图,已知直线AB和CD相交于点O,OE⊥OC,OF平分∠AOE.若∠COF=36°,则∠BOD的度数为( )
A.20° B.18° C.16° D.14°
10.如图,直线l1,l2被直线l3所截,则下列各组中的两个角是同位角的是( )
A.∠3与∠4 B.∠2与∠4 C.∠1与∠3 D.∠1与∠2
11.如图,点O在直线AB上,OC⊥OD,若∠AOC=150°,则∠BOD的大小为( )
A.30° B.40° C.50° D.60°
12.若点A到直线l的距离为7cm,点B到直线l的距离为3cm,则线段AB的长度为( )
A.10cm B.4cm C.10cm或4cm D.至少4cm
二.填空题(共5小题)
13.如图,在灌溉时,要把河中的水引到农田P处,农民李伯伯的做法是:过点P作PM垂直于河岸l,垂足为M,沿PM开挖水渠距离最短,其中的数学道理是 .
14.在直角三角形ABC中,∠ACB=90°,AC=6,BC=8,AB=10,则点C到AB的距离为 .
15.如图,直线AB、CD相交于点O,OE平分∠BOD,若∠AOD=100°,则∠BOE= .
16.如图,直线AB,CD相交于点O,EO⊥CD.若∠AOE=2∠AOC,则∠BOD的度数为 °.
17.已知∠1和∠2互为邻补角,若∠1=80°,则∠2=
三.解答题(共5小题)
18.如图,直线AB、CD交于点O,OP⊥CD于点O,如果OA平分∠POD,求∠BOC的度数.
19.如图,直线AB,CD相交于点O.已知,∠EOC:∠EOD=4:5,OA平分∠EOC,求∠AOC的度数.
20.平面内两条直线EF、CD相交于点O,OA⊥OB,OC恰好平分∠AOF.
(1)如图1,若∠AOE=40°,求∠BOD的度数;
(2)在图1中,若∠AOE=x°,请求出∠BOD的度数(用含有x的式子表示),并写出∠AOE和∠BOD的数量关系;
(3)如图2,当OA,OB在直线EF的同侧时,∠AOE和∠BOD的数量关系是否会发生改变?若不变,请直接写出它们之间的数量关系;若发生变化,请说明理由.
21.如图,直线AB、CD相交于点O,OM⊥AB.
(1)若∠1=∠2,证明:ON⊥CD;
(2)若∠1=∠BOC,求∠BOD的度数.
22.如图,直线AB,CD相交于点O,OE⊥AB,垂足为O.
(1)直接写出图中∠AOC的对顶角为 ,∠BOD的邻补角为 ;
(2)若∠BOD:∠COE=1:2,求∠AOD的度数.
参考答案
一.选择题(共12小题)
1--10BACBC DBCBB 11--12DD
二.填空题(共5小题)
13.垂线段最短.
14.4.8.
15.40°.
16.30.
17.100°.
三.解答题(共5小题)
18.解:∵OP⊥CD,
∴∠DOP=90°,
又∵OA平分∠POD,
∴∠AOD=∠POD=45°,
∴∠BOC=∠AOD=45°.
19.解:∵∠EOC:∠EOD=4:5,∠EOC+∠EOD=180°,
∴∠EOC=×180°=80°,
∵OA平分∠EOC,
∴∠AOC=∠AOE=∠EOC=40°.
20.解:(1)∵∠AOE=40°,
∴∠AOF=180°﹣∠AOE=140°,
∵OC平分∠AOF,
∴,
∵OA⊥OB,
∴∠AOB=90°,
∴∠BOD=180°﹣∠AOB﹣∠AOC=20°;
(2)∵∠AOE=x°,
∴∠AOF=180°﹣∠AOE=(180﹣x)°,
∵OC平分∠AOF,
∴,
∵OA⊥OB,
∴∠AOB=90°,
∴;
∴∠AOE=2∠BOD;
(3)不变,∠AOE=2∠BOD.
21.证明:(1)∵OM⊥AB,
∴∠AOM=∠BOM=90°,
∴∠1+∠AOC=90°,
∵∠1=∠2,
∴∠2+∠AOC=90°,
即∠CON=90°,
∴ON⊥CD;
(2)∵∠1=∠BOC,
∴∠BOM=2∠1=90°,
解得:∠1=45°,
∴∠BOD=90°﹣45°=45°
22.解:(1)∠AOC的对顶角为∠BOD,∠BOD的邻补角为∠AOD,∠BOC,
(2)∵OE⊥AB,
∴∠AOE=90°,
∴∠AOC+∠COE=90°,
∵∠BOD=∠AOC,
∵∠BOD:∠COE=1:2,
∴∠BOD=30°,
∴∠AOD=150°,
故答案为:∠BOD;∠AOD,∠BOC
