17.1.2 勾股定理的实际应用 同步训练(含答案)数学人教版八年级下册
文档属性
| 名称 | 17.1.2 勾股定理的实际应用 同步训练(含答案)数学人教版八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 218.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-10 13:45:18 | ||
图片预览



文档简介
第十七章 勾股定理
17.1 勾股定理
第2课时 勾股定理的实际应用
一、选择题
1.长方形花园长80m,宽比长短20m,把对角线修成一条小路,这条小路的长为( )
A.60m B.100m
C.130m D.150m
2.一架5m长的梯子斜靠在建筑物上,如果梯子的底端离建筑物3m远,那么该梯子可以达到建筑物的高度是( )
A.2m B.3m C.4m D.5m
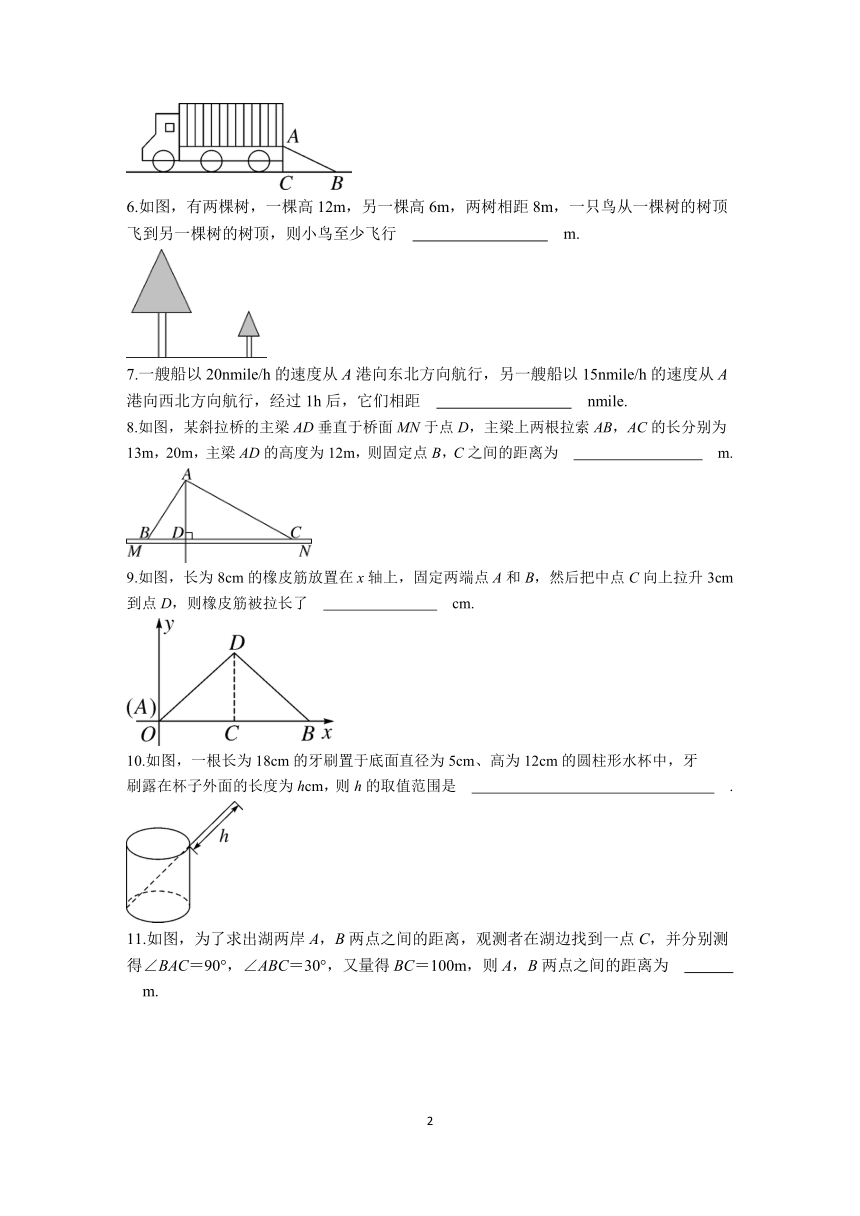
3.如图,将一张长为20cm,宽为15cm的长方形纸(AE>DE)剪去了一角,量得AB=3cm,CD=4cm,则剪去的直角三角形的斜边长为( )
A.5cm B.12cm
C.16cm D.20cm
4.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7m,顶端距离地面2.4m.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2m,那么小巷的宽度为( )
A.0.7m B.1.5m
C.2.2m D.2.4m
二、填空题
5.如图,货车卸货时支架侧面是Rt△ABC,其中∠ACB=90°.已知AB=2.5m,BC=2m,则AC的长为 m.
6.如图,有两棵树,一棵高12m,另一棵高6m,两树相距8m,一只鸟从一棵树的树顶飞到另一棵树的树顶,则小鸟至少飞行 m.
7.一艘船以20nmile/h的速度从A港向东北方向航行,另一艘船以15nmile/h的速度从A港向西北方向航行,经过1h后,它们相距 nmile.
8.如图,某斜拉桥的主梁AD垂直于桥面MN于点D,主梁上两根拉索AB,AC的长分别为13m,20m,主梁AD的高度为12m,则固定点B,C之间的距离为 m.
9.如图,长为8cm的橡皮筋放置在x轴上,固定两端点A和B,然后把中点C向上拉升3cm到点D,则橡皮筋被拉长了 cm.
10.如图,一根长为18cm的牙刷置于底面直径为5cm、高为12cm的圆柱形水杯中,牙
刷露在杯子外面的长度为hcm,则h的取值范围是 .
11.如图,为了求出湖两岸A,B两点之间的距离,观测者在湖边找到一点C,并分别测得∠BAC=90°,∠ABC=30°,又量得BC=100m,则A,B两点之间的距离为 m.
三、解答题
12.某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离了欲到达点B240m.已知他在水中游了510m,求该河的宽度(两岸可近似看作平行).
13.如图,小颖和她的同学荡秋千,秋千AB在静止位置时,下端B'离地面0.6m,荡秋千到AB的位置时,下端B距静止位置的水平距离EB等于2.4m,距地面1.4m,求秋千AB的长.
14.由于大风,山坡上的一棵树甲在点A处被拦腰折断,如图所示,其树顶端恰好落在另一棵树乙的根部点C处.已知AB=4m,BC=13m,两棵树的水平距离为12m,求甲树原来的高度.
15.吴老师在与同学们进行“蚂蚁怎样爬最近”的课题研究时设计了以下问题,请你根据下列所给的条件分别求出蚂蚁需要爬行的最短路程.
(1)如图①,圆柱的高为8cm,底面周长为12cm,一只蚂蚁欲沿圆柱侧面从点A爬到相对的点B处,需要爬行的最短路程是 cm;
(2)如图②,正方体的棱长为5cm,一只蚂蚁欲从顶点A处沿表面爬到顶点C1处;
(3)如图③,长方体底面是边长为5cm的正方形,高为6cm,一只蚂蚁欲从顶点A处沿表面爬到顶点C1处.
9
参考答案
一、选择题
1.长方形花园长80m,宽比长短20m,把对角线修成一条小路,这条小路的长为( B )
A.60m B.100m
C.130m D.150m
2.一架5m长的梯子斜靠在建筑物上,如果梯子的底端离建筑物3m远,那么该梯子可以达到建筑物的高度是( C )
A.2m B.3m C.4m D.5m
3.如图,将一张长为20cm,宽为15cm的长方形纸(AE>DE)剪去了一角,量得AB=3cm,CD=4cm,则剪去的直角三角形的斜边长为( D )
A.5cm B.12cm
C.16cm D.20cm
4.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7m,顶端距离地面2.4m.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2m,那么小巷的宽度为( C )
A.0.7m B.1.5m
C.2.2m D.2.4m
二、填空题
5.如图,货车卸货时支架侧面是Rt△ABC,其中∠ACB=90°.已知AB=2.5m,BC=2m,则AC的长为 m.
【答案】1.5
6.如图,有两棵树,一棵高12m,另一棵高6m,两树相距8m,一只鸟从一棵树的树顶飞到另一棵树的树顶,则小鸟至少飞行 m.
【答案】10
7.一艘船以20nmile/h的速度从A港向东北方向航行,另一艘船以15nmile/h的速度从A港向西北方向航行,经过1h后,它们相距 nmile.
【答案】25
8.如图,某斜拉桥的主梁AD垂直于桥面MN于点D,主梁上两根拉索AB,AC的长分别为13m,20m,主梁AD的高度为12m,则固定点B,C之间的距离为 m.
【答案】21
9.如图,长为8cm的橡皮筋放置在x轴上,固定两端点A和B,然后把中点C向上拉升3cm到点D,则橡皮筋被拉长了 cm.
【答案】2
10.如图,一根长为18cm的牙刷置于底面直径为5cm、高为12cm的圆柱形水杯中,牙
刷露在杯子外面的长度为hcm,则h的取值范围是 .
【答案】5≤h≤6
11.如图,为了求出湖两岸A,B两点之间的距离,观测者在湖边找到一点C,并分别测得∠BAC=90°,∠ABC=30°,又量得BC=100m,则A,B两点之间的距离为 m.
【答案】5
三、解答题
12.某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离了欲到达点B240m.已知他在水中游了510m,求该河的宽度(两岸可近似看作平行).
解:根据题意得∠ABC=90°,
则AB===450(m),
即该河的宽度为450m.
13.如图,小颖和她的同学荡秋千,秋千AB在静止位置时,下端B'离地面0.6m,荡秋千到AB的位置时,下端B距静止位置的水平距离EB等于2.4m,距地面1.4m,求秋千AB的长.
解:设AB=AB'=xm,
由题意得B'E=1.4-0.6=0.8(m),
则AE=(x-0.8)m.
在Rt△AEB中,∵AE2+BE2=AB2,
∴(x-0.8)2+2.42=x2.
解得x=4.
答:秋千AB的长为4m.
14.由于大风,山坡上的一棵树甲在点A处被拦腰折断,如图所示,其树顶端恰好落在另一棵树乙的根部点C处.已知AB=4m,BC=13m,两棵树的水平距离为12m,求甲树原来的高度.
解:如图,过点C作CD⊥AB交AB的延长线于点D.
由题意可得BC=13m,DC=12m,
故BD==5(m).即AD=9m,
则AC===15(m).
故AC+AB=15+4=19(m).
答:甲树原来的高度是19m.
15.吴老师在与同学们进行“蚂蚁怎样爬最近”的课题研究时设计了以下问题,请你根据下列所给的条件分别求出蚂蚁需要爬行的最短路程.
(1)如图①,圆柱的高为8cm,底面周长为12cm,一只蚂蚁欲沿圆柱侧面从点A爬到相对的点B处,需要爬行的最短路程是 cm;
【答案】10
(2)如图②,正方体的棱长为5cm,一只蚂蚁欲从顶点A处沿表面爬到顶点C1处;
(3)如图③,长方体底面是边长为5cm的正方形,高为6cm,一只蚂蚁欲从顶点A处沿表面爬到顶点C1处.
解:(2)如图a,将正方体沿A1B1展开,AC1===5(cm).
易知将正方体分别沿BB1,A1D1展开后,
均有AC1=5cm.
∴蚂蚁需要爬行的最短路程为5cm.
(3)如图b,将长方体沿BB1展开,AC1==2(cm);
如图c,将长方体沿A1B1展开,AC1==(cm).
易知将长方体沿A1D1展开,有AC1=cm.
∵>2,
∴蚂蚁需要爬行的最短路程为2cm.
17.1 勾股定理
第2课时 勾股定理的实际应用
一、选择题
1.长方形花园长80m,宽比长短20m,把对角线修成一条小路,这条小路的长为( )
A.60m B.100m
C.130m D.150m
2.一架5m长的梯子斜靠在建筑物上,如果梯子的底端离建筑物3m远,那么该梯子可以达到建筑物的高度是( )
A.2m B.3m C.4m D.5m
3.如图,将一张长为20cm,宽为15cm的长方形纸(AE>DE)剪去了一角,量得AB=3cm,CD=4cm,则剪去的直角三角形的斜边长为( )
A.5cm B.12cm
C.16cm D.20cm
4.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7m,顶端距离地面2.4m.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2m,那么小巷的宽度为( )
A.0.7m B.1.5m
C.2.2m D.2.4m
二、填空题
5.如图,货车卸货时支架侧面是Rt△ABC,其中∠ACB=90°.已知AB=2.5m,BC=2m,则AC的长为 m.
6.如图,有两棵树,一棵高12m,另一棵高6m,两树相距8m,一只鸟从一棵树的树顶飞到另一棵树的树顶,则小鸟至少飞行 m.
7.一艘船以20nmile/h的速度从A港向东北方向航行,另一艘船以15nmile/h的速度从A港向西北方向航行,经过1h后,它们相距 nmile.
8.如图,某斜拉桥的主梁AD垂直于桥面MN于点D,主梁上两根拉索AB,AC的长分别为13m,20m,主梁AD的高度为12m,则固定点B,C之间的距离为 m.
9.如图,长为8cm的橡皮筋放置在x轴上,固定两端点A和B,然后把中点C向上拉升3cm到点D,则橡皮筋被拉长了 cm.
10.如图,一根长为18cm的牙刷置于底面直径为5cm、高为12cm的圆柱形水杯中,牙
刷露在杯子外面的长度为hcm,则h的取值范围是 .
11.如图,为了求出湖两岸A,B两点之间的距离,观测者在湖边找到一点C,并分别测得∠BAC=90°,∠ABC=30°,又量得BC=100m,则A,B两点之间的距离为 m.
三、解答题
12.某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离了欲到达点B240m.已知他在水中游了510m,求该河的宽度(两岸可近似看作平行).
13.如图,小颖和她的同学荡秋千,秋千AB在静止位置时,下端B'离地面0.6m,荡秋千到AB的位置时,下端B距静止位置的水平距离EB等于2.4m,距地面1.4m,求秋千AB的长.
14.由于大风,山坡上的一棵树甲在点A处被拦腰折断,如图所示,其树顶端恰好落在另一棵树乙的根部点C处.已知AB=4m,BC=13m,两棵树的水平距离为12m,求甲树原来的高度.
15.吴老师在与同学们进行“蚂蚁怎样爬最近”的课题研究时设计了以下问题,请你根据下列所给的条件分别求出蚂蚁需要爬行的最短路程.
(1)如图①,圆柱的高为8cm,底面周长为12cm,一只蚂蚁欲沿圆柱侧面从点A爬到相对的点B处,需要爬行的最短路程是 cm;
(2)如图②,正方体的棱长为5cm,一只蚂蚁欲从顶点A处沿表面爬到顶点C1处;
(3)如图③,长方体底面是边长为5cm的正方形,高为6cm,一只蚂蚁欲从顶点A处沿表面爬到顶点C1处.
9
参考答案
一、选择题
1.长方形花园长80m,宽比长短20m,把对角线修成一条小路,这条小路的长为( B )
A.60m B.100m
C.130m D.150m
2.一架5m长的梯子斜靠在建筑物上,如果梯子的底端离建筑物3m远,那么该梯子可以达到建筑物的高度是( C )
A.2m B.3m C.4m D.5m
3.如图,将一张长为20cm,宽为15cm的长方形纸(AE>DE)剪去了一角,量得AB=3cm,CD=4cm,则剪去的直角三角形的斜边长为( D )
A.5cm B.12cm
C.16cm D.20cm
4.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7m,顶端距离地面2.4m.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2m,那么小巷的宽度为( C )
A.0.7m B.1.5m
C.2.2m D.2.4m
二、填空题
5.如图,货车卸货时支架侧面是Rt△ABC,其中∠ACB=90°.已知AB=2.5m,BC=2m,则AC的长为 m.
【答案】1.5
6.如图,有两棵树,一棵高12m,另一棵高6m,两树相距8m,一只鸟从一棵树的树顶飞到另一棵树的树顶,则小鸟至少飞行 m.
【答案】10
7.一艘船以20nmile/h的速度从A港向东北方向航行,另一艘船以15nmile/h的速度从A港向西北方向航行,经过1h后,它们相距 nmile.
【答案】25
8.如图,某斜拉桥的主梁AD垂直于桥面MN于点D,主梁上两根拉索AB,AC的长分别为13m,20m,主梁AD的高度为12m,则固定点B,C之间的距离为 m.
【答案】21
9.如图,长为8cm的橡皮筋放置在x轴上,固定两端点A和B,然后把中点C向上拉升3cm到点D,则橡皮筋被拉长了 cm.
【答案】2
10.如图,一根长为18cm的牙刷置于底面直径为5cm、高为12cm的圆柱形水杯中,牙
刷露在杯子外面的长度为hcm,则h的取值范围是 .
【答案】5≤h≤6
11.如图,为了求出湖两岸A,B两点之间的距离,观测者在湖边找到一点C,并分别测得∠BAC=90°,∠ABC=30°,又量得BC=100m,则A,B两点之间的距离为 m.
【答案】5
三、解答题
12.某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离了欲到达点B240m.已知他在水中游了510m,求该河的宽度(两岸可近似看作平行).
解:根据题意得∠ABC=90°,
则AB===450(m),
即该河的宽度为450m.
13.如图,小颖和她的同学荡秋千,秋千AB在静止位置时,下端B'离地面0.6m,荡秋千到AB的位置时,下端B距静止位置的水平距离EB等于2.4m,距地面1.4m,求秋千AB的长.
解:设AB=AB'=xm,
由题意得B'E=1.4-0.6=0.8(m),
则AE=(x-0.8)m.
在Rt△AEB中,∵AE2+BE2=AB2,
∴(x-0.8)2+2.42=x2.
解得x=4.
答:秋千AB的长为4m.
14.由于大风,山坡上的一棵树甲在点A处被拦腰折断,如图所示,其树顶端恰好落在另一棵树乙的根部点C处.已知AB=4m,BC=13m,两棵树的水平距离为12m,求甲树原来的高度.
解:如图,过点C作CD⊥AB交AB的延长线于点D.
由题意可得BC=13m,DC=12m,
故BD==5(m).即AD=9m,
则AC===15(m).
故AC+AB=15+4=19(m).
答:甲树原来的高度是19m.
15.吴老师在与同学们进行“蚂蚁怎样爬最近”的课题研究时设计了以下问题,请你根据下列所给的条件分别求出蚂蚁需要爬行的最短路程.
(1)如图①,圆柱的高为8cm,底面周长为12cm,一只蚂蚁欲沿圆柱侧面从点A爬到相对的点B处,需要爬行的最短路程是 cm;
【答案】10
(2)如图②,正方体的棱长为5cm,一只蚂蚁欲从顶点A处沿表面爬到顶点C1处;
(3)如图③,长方体底面是边长为5cm的正方形,高为6cm,一只蚂蚁欲从顶点A处沿表面爬到顶点C1处.
解:(2)如图a,将正方体沿A1B1展开,AC1===5(cm).
易知将正方体分别沿BB1,A1D1展开后,
均有AC1=5cm.
∴蚂蚁需要爬行的最短路程为5cm.
(3)如图b,将长方体沿BB1展开,AC1==2(cm);
如图c,将长方体沿A1B1展开,AC1==(cm).
易知将长方体沿A1D1展开,有AC1=cm.
∵>2,
∴蚂蚁需要爬行的最短路程为2cm.
