人教版数学八年级下册17.1.3 利用勾股定理作图或计算 同步训练(含答案)
文档属性
| 名称 | 人教版数学八年级下册17.1.3 利用勾股定理作图或计算 同步训练(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 199.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-10 15:52:40 | ||
图片预览


文档简介
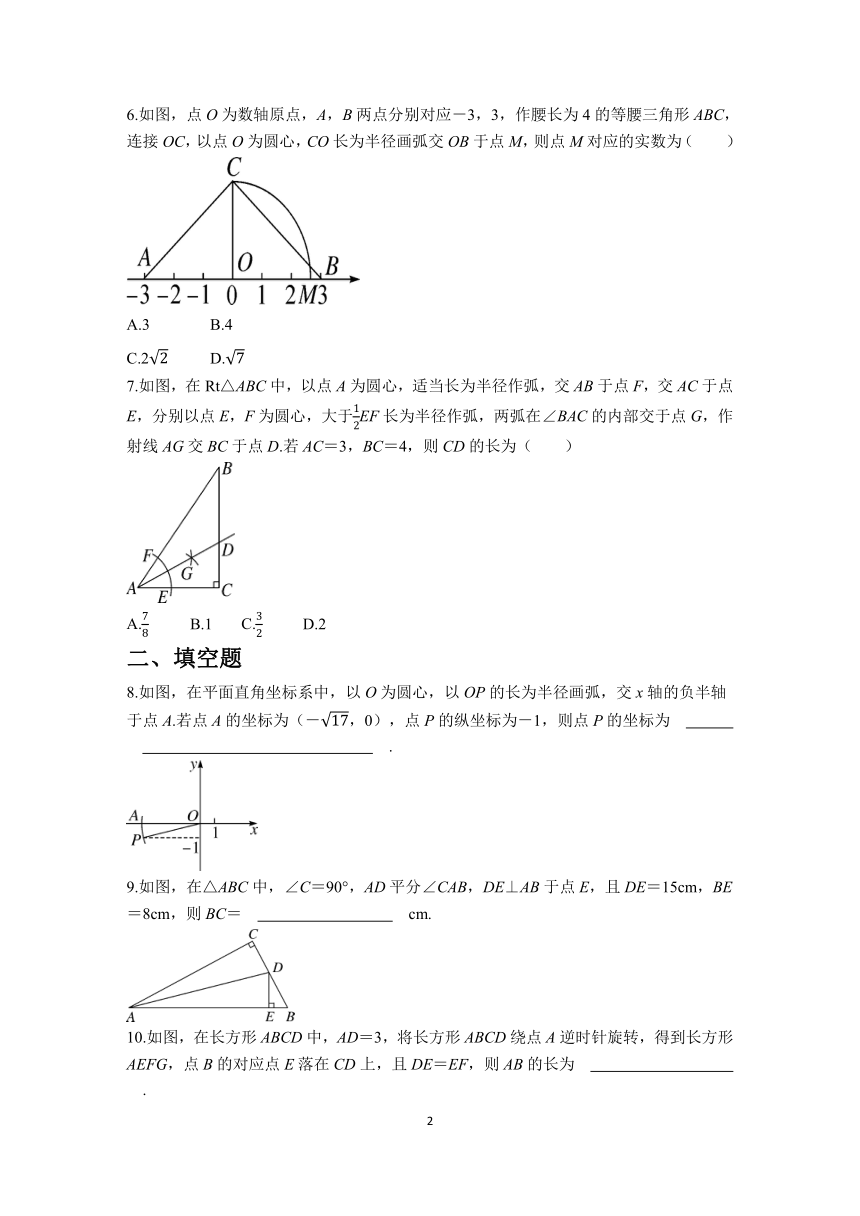
第十七章 勾股定理
17.1 勾股定理
第3课时 利用勾股定理作图或计算
一、选择题
1.在平面直角坐标系中,点P(4,3)到原点的距离是( )
A.3 B.4
C.5 D.7
2.如图,数轴上的点A所表示的数为x,则x的值为( )
A. B.- C.2 D.-2
3.在Rt△ABC中,∠C=90°,c为斜边,a,b为直角边,a+b=14,c=10,则Rt△ABC的面积为( )
A.24 B.36
C.48 D.60
4.如图,网格中每个小正方形的边长均为1,点A,B为网格线的交点,则线段AB的长为( )
A.3 B.5 C.7 D.12
5.如图,a,b,c是3×3的正方形网格中的3条线段,它们的端点都在格点上,则关于a,b,c大小关系的正确判断是( )
A.b<a<c B.a<b<c
C.a<c<b D.b<c<a
6.如图,点O为数轴原点,A,B两点分别对应-3,3,作腰长为4的等腰三角形ABC,连接OC,以点O为圆心,CO长为半径画弧交OB于点M,则点M对应的实数为( )
A.3 B.4
C.2 D.
7.如图,在Rt△ABC中,以点A为圆心,适当长为半径作弧,交AB于点F,交AC于点E,分别以点E,F为圆心,大于EF长为半径作弧,两弧在∠BAC的内部交于点G,作射线AG交BC于点D.若AC=3,BC=4,则CD的长为( )
A. B.1 C. D.2
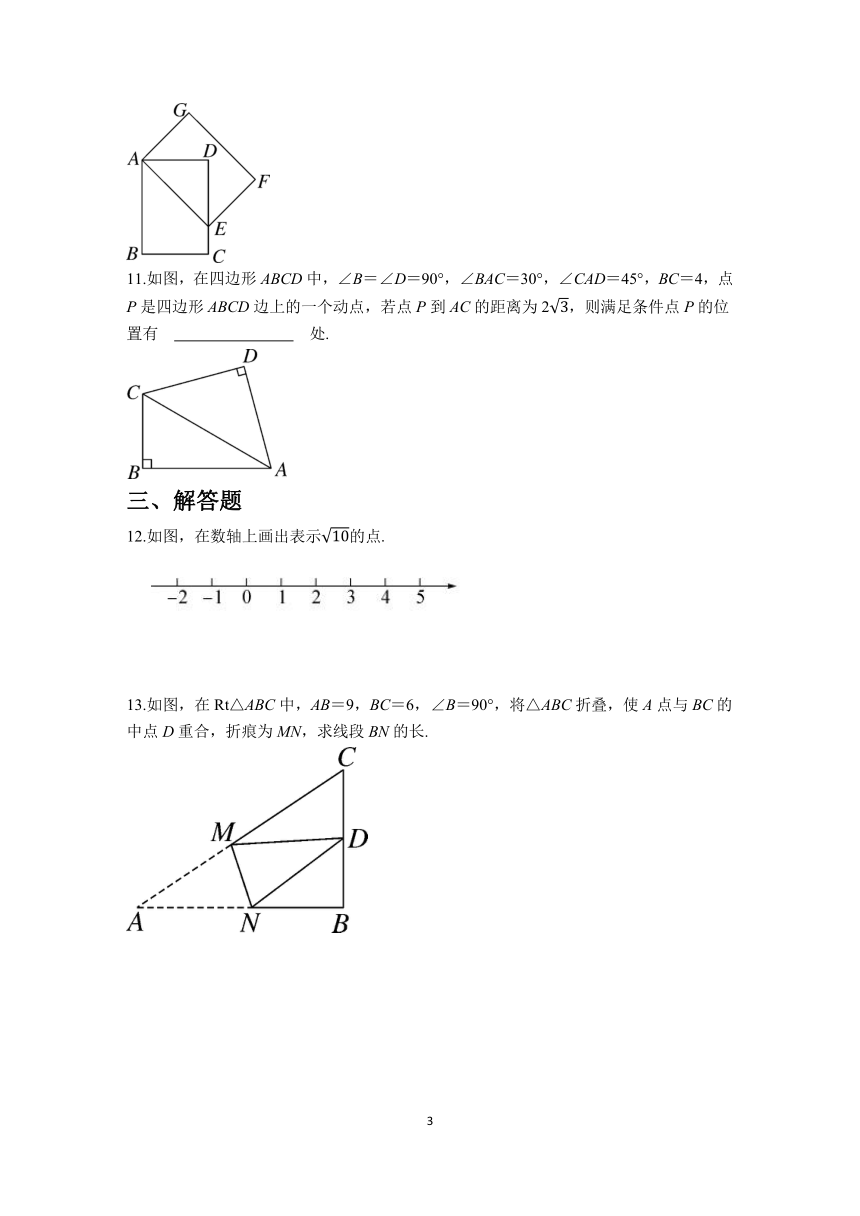
二、填空题
8.如图,在平面直角坐标系中,以O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A.若点A的坐标为(-,0),点P的纵坐标为-1,则点P的坐标为 .
9.如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,且DE=15cm,BE=8cm,则BC= cm.
10.如图,在长方形ABCD中,AD=3,将长方形ABCD绕点A逆时针旋转,得到长方形AEFG,点B的对应点E落在CD上,且DE=EF,则AB的长为 .
11.如图,在四边形ABCD中,∠B=∠D=90°,∠BAC=30°,∠CAD=45°,BC=4,点P是四边形ABCD边上的一个动点,若点P到AC的距离为2,则满足条件点P的位置有 处.
三、解答题
12.如图,在数轴上画出表示的点.
13.如图,在Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,求线段BN的长.
14.如图,在△ABC中,∠C=90°,BC=6cm,AC=8cm,D为AC上一点,将△BCD沿BD折叠,点C刚好落在AB边上的点E处,求△AED的面积.
15.图甲是第七届国际数学教育大会的会徽,会徽的主体图案是由图乙中的一连串直角三角形演化而成的,其中OA1=A1A2=A2A3=…=A7A8=1.细心观察图形,认真分析下列各式,然后解答问题:
()2+1=2,S1=;
()2+1=3,S2=;()2+1=4,S3=;
……
(1)请用含有n(n是正整数)的等式表示上述变化规律,并计算出OA10的长;
(2)求出+++…+的值.
4
参考答案
一、选择题
1.在平面直角坐标系中,点P(4,3)到原点的距离是( C )
A.3 B.4
C.5 D.7
2.如图,数轴上的点A所表示的数为x,则x的值为( B )
A. B.- C.2 D.-2
3.在Rt△ABC中,∠C=90°,c为斜边,a,b为直角边,a+b=14,c=10,则Rt△ABC的面积为( A )
A.24 B.36
C.48 D.60
4.如图,网格中每个小正方形的边长均为1,点A,B为网格线的交点,则线段AB的长为( B )
A.3 B.5 C.7 D.12
5.如图,a,b,c是3×3的正方形网格中的3条线段,它们的端点都在格点上,则关于a,b,c大小关系的正确判断是( B )
A.b<a<c B.a<b<c
C.a<c<b D.b<c<a
6.如图,点O为数轴原点,A,B两点分别对应-3,3,作腰长为4的等腰三角形ABC,连接OC,以点O为圆心,CO长为半径画弧交OB于点M,则点M对应的实数为( D )
A.3 B.4
C.2 D.
7.如图,在Rt△ABC中,以点A为圆心,适当长为半径作弧,交AB于点F,交AC于点E,分别以点E,F为圆心,大于EF长为半径作弧,两弧在∠BAC的内部交于点G,作射线AG交BC于点D.若AC=3,BC=4,则CD的长为( C )
A. B.1 C. D.2
二、填空题
8.如图,在平面直角坐标系中,以O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A.若点A的坐标为(-,0),点P的纵坐标为-1,则点P的坐标为 .
【答案】(-4,-1)
9.如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,且DE=15cm,BE=8cm,则BC= cm.
【答案】32
10.如图,在长方形ABCD中,AD=3,将长方形ABCD绕点A逆时针旋转,得到长方形AEFG,点B的对应点E落在CD上,且DE=EF,则AB的长为 .
【答案】3
11.如图,在四边形ABCD中,∠B=∠D=90°,∠BAC=30°,∠CAD=45°,BC=4,点P是四边形ABCD边上的一个动点,若点P到AC的距离为2,则满足条件点P的位置有 处.
【答案】3
三、解答题
12.如图,在数轴上画出表示的点.
解:如图,在数轴上找出表示3的点A,
则OA=3,过点A作直线l垂直于OA,
在l上取点B,使AB=1.
以点O为圆心,OB的长为半径画弧,交数轴正半轴于点
C则点C为表示的点.
13.如图,在Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,求线段BN的长.
解:已知AB=9,BC=6,
设BN=x,由折叠的性质可得DN=AN=AB-BN=9-x.
∵点D是BC的中点,
∴BD=BC=3.
在Rt△BND中,
由勾股定理得BN2+BD2=DN2,
即x2+32=(9-x)2,解得x=4.
即线段BN的长为4.
14.如图,在△ABC中,∠C=90°,BC=6cm,AC=8cm,D为AC上一点,将△BCD沿BD折叠,点C刚好落在AB边上的点E处,求△AED的面积.
解:在△ABC中,
∵∠C=90°,BC=6cm,AC=8cm,
∴AB===10(cm).
由题意得BE=BC=6cm,DE=CD,∠BED=∠C=90°
∴∠AED=90°,AE=AB-BE=4cm.
设CD=xcm,则DE=xcm,AD=(8-x)cm.
在Rt△AED中,
∵AD2=AE2+DE2,
∴(8-x)2=42+x2.
解得x=3.
∴DE=3cm.
则S△AED=AE·DE=×4×3=6(cm2).
15.图甲是第七届国际数学教育大会的会徽,会徽的主体图案是由图乙中的一连串直角三角形演化而成的,其中OA1=A1A2=A2A3=…=A7A8=1.细心观察图形,认真分析下列各式,然后解答问题:
()2+1=2,S1=;
()2+1=3,S2=;()2+1=4,S3=;
……
(1)请用含有n(n是正整数)的等式表示上述变化规律,并计算出OA10的长;
解:(1)()2+1=n+1,Sn=.OA10=.
(2)求出+++…+的值.
(2)+++…+=()2+()2+()2+…+()2==.
17.1 勾股定理
第3课时 利用勾股定理作图或计算
一、选择题
1.在平面直角坐标系中,点P(4,3)到原点的距离是( )
A.3 B.4
C.5 D.7
2.如图,数轴上的点A所表示的数为x,则x的值为( )
A. B.- C.2 D.-2
3.在Rt△ABC中,∠C=90°,c为斜边,a,b为直角边,a+b=14,c=10,则Rt△ABC的面积为( )
A.24 B.36
C.48 D.60
4.如图,网格中每个小正方形的边长均为1,点A,B为网格线的交点,则线段AB的长为( )
A.3 B.5 C.7 D.12
5.如图,a,b,c是3×3的正方形网格中的3条线段,它们的端点都在格点上,则关于a,b,c大小关系的正确判断是( )
A.b<a<c B.a<b<c
C.a<c<b D.b<c<a
6.如图,点O为数轴原点,A,B两点分别对应-3,3,作腰长为4的等腰三角形ABC,连接OC,以点O为圆心,CO长为半径画弧交OB于点M,则点M对应的实数为( )
A.3 B.4
C.2 D.
7.如图,在Rt△ABC中,以点A为圆心,适当长为半径作弧,交AB于点F,交AC于点E,分别以点E,F为圆心,大于EF长为半径作弧,两弧在∠BAC的内部交于点G,作射线AG交BC于点D.若AC=3,BC=4,则CD的长为( )
A. B.1 C. D.2
二、填空题
8.如图,在平面直角坐标系中,以O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A.若点A的坐标为(-,0),点P的纵坐标为-1,则点P的坐标为 .
9.如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,且DE=15cm,BE=8cm,则BC= cm.
10.如图,在长方形ABCD中,AD=3,将长方形ABCD绕点A逆时针旋转,得到长方形AEFG,点B的对应点E落在CD上,且DE=EF,则AB的长为 .
11.如图,在四边形ABCD中,∠B=∠D=90°,∠BAC=30°,∠CAD=45°,BC=4,点P是四边形ABCD边上的一个动点,若点P到AC的距离为2,则满足条件点P的位置有 处.
三、解答题
12.如图,在数轴上画出表示的点.
13.如图,在Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,求线段BN的长.
14.如图,在△ABC中,∠C=90°,BC=6cm,AC=8cm,D为AC上一点,将△BCD沿BD折叠,点C刚好落在AB边上的点E处,求△AED的面积.
15.图甲是第七届国际数学教育大会的会徽,会徽的主体图案是由图乙中的一连串直角三角形演化而成的,其中OA1=A1A2=A2A3=…=A7A8=1.细心观察图形,认真分析下列各式,然后解答问题:
()2+1=2,S1=;
()2+1=3,S2=;()2+1=4,S3=;
……
(1)请用含有n(n是正整数)的等式表示上述变化规律,并计算出OA10的长;
(2)求出+++…+的值.
4
参考答案
一、选择题
1.在平面直角坐标系中,点P(4,3)到原点的距离是( C )
A.3 B.4
C.5 D.7
2.如图,数轴上的点A所表示的数为x,则x的值为( B )
A. B.- C.2 D.-2
3.在Rt△ABC中,∠C=90°,c为斜边,a,b为直角边,a+b=14,c=10,则Rt△ABC的面积为( A )
A.24 B.36
C.48 D.60
4.如图,网格中每个小正方形的边长均为1,点A,B为网格线的交点,则线段AB的长为( B )
A.3 B.5 C.7 D.12
5.如图,a,b,c是3×3的正方形网格中的3条线段,它们的端点都在格点上,则关于a,b,c大小关系的正确判断是( B )
A.b<a<c B.a<b<c
C.a<c<b D.b<c<a
6.如图,点O为数轴原点,A,B两点分别对应-3,3,作腰长为4的等腰三角形ABC,连接OC,以点O为圆心,CO长为半径画弧交OB于点M,则点M对应的实数为( D )
A.3 B.4
C.2 D.
7.如图,在Rt△ABC中,以点A为圆心,适当长为半径作弧,交AB于点F,交AC于点E,分别以点E,F为圆心,大于EF长为半径作弧,两弧在∠BAC的内部交于点G,作射线AG交BC于点D.若AC=3,BC=4,则CD的长为( C )
A. B.1 C. D.2
二、填空题
8.如图,在平面直角坐标系中,以O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A.若点A的坐标为(-,0),点P的纵坐标为-1,则点P的坐标为 .
【答案】(-4,-1)
9.如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,且DE=15cm,BE=8cm,则BC= cm.
【答案】32
10.如图,在长方形ABCD中,AD=3,将长方形ABCD绕点A逆时针旋转,得到长方形AEFG,点B的对应点E落在CD上,且DE=EF,则AB的长为 .
【答案】3
11.如图,在四边形ABCD中,∠B=∠D=90°,∠BAC=30°,∠CAD=45°,BC=4,点P是四边形ABCD边上的一个动点,若点P到AC的距离为2,则满足条件点P的位置有 处.
【答案】3
三、解答题
12.如图,在数轴上画出表示的点.
解:如图,在数轴上找出表示3的点A,
则OA=3,过点A作直线l垂直于OA,
在l上取点B,使AB=1.
以点O为圆心,OB的长为半径画弧,交数轴正半轴于点
C则点C为表示的点.
13.如图,在Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,求线段BN的长.
解:已知AB=9,BC=6,
设BN=x,由折叠的性质可得DN=AN=AB-BN=9-x.
∵点D是BC的中点,
∴BD=BC=3.
在Rt△BND中,
由勾股定理得BN2+BD2=DN2,
即x2+32=(9-x)2,解得x=4.
即线段BN的长为4.
14.如图,在△ABC中,∠C=90°,BC=6cm,AC=8cm,D为AC上一点,将△BCD沿BD折叠,点C刚好落在AB边上的点E处,求△AED的面积.
解:在△ABC中,
∵∠C=90°,BC=6cm,AC=8cm,
∴AB===10(cm).
由题意得BE=BC=6cm,DE=CD,∠BED=∠C=90°
∴∠AED=90°,AE=AB-BE=4cm.
设CD=xcm,则DE=xcm,AD=(8-x)cm.
在Rt△AED中,
∵AD2=AE2+DE2,
∴(8-x)2=42+x2.
解得x=3.
∴DE=3cm.
则S△AED=AE·DE=×4×3=6(cm2).
15.图甲是第七届国际数学教育大会的会徽,会徽的主体图案是由图乙中的一连串直角三角形演化而成的,其中OA1=A1A2=A2A3=…=A7A8=1.细心观察图形,认真分析下列各式,然后解答问题:
()2+1=2,S1=;
()2+1=3,S2=;()2+1=4,S3=;
……
(1)请用含有n(n是正整数)的等式表示上述变化规律,并计算出OA10的长;
解:(1)()2+1=n+1,Sn=.OA10=.
(2)求出+++…+的值.
(2)+++…+=()2+()2+()2+…+()2==.
