17.2.1 勾股定理的逆定理 同步训练(原卷 +答案)人教版数学八年级下册
文档属性
| 名称 | 17.2.1 勾股定理的逆定理 同步训练(原卷 +答案)人教版数学八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 129.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-10 16:29:10 | ||
图片预览


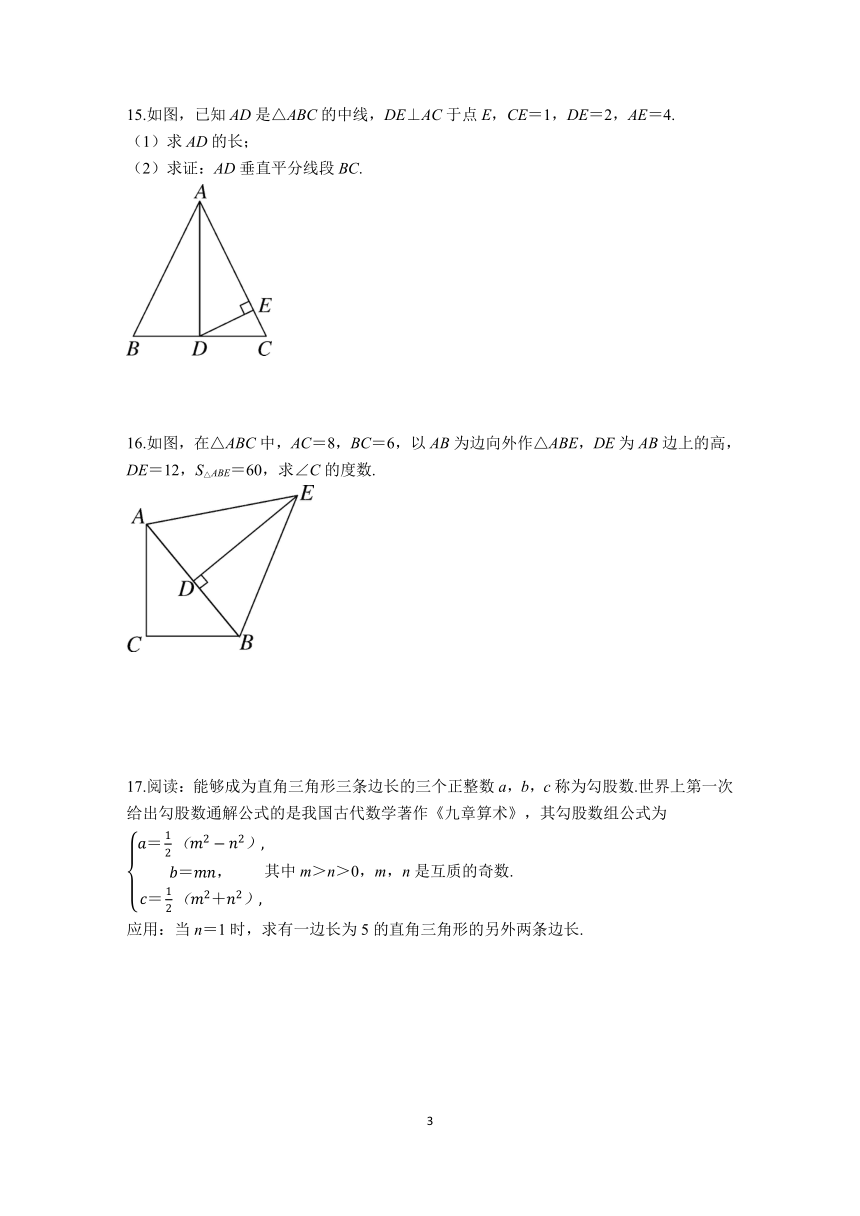
文档简介
第十七章 勾股定理
17.2 勾股定理的逆定理
第1课时 勾股定理的逆定理
一、选择题
1.下列各组数中,不能作为直角三角形三边长的是( )
A.3,4,5 B.4,5,6
C.6,8,10 D.5,12,13
2.如果三角形的三边长分别为,,2,那么这个三角形的最大内角的度数为( )
A.30° B.45° C.60° D.90°
3.下列各组数中,是勾股数的是( )
A.,, B.,,
C.0.3,0.4,0.5 D.25,60,65
4.已知下列命题:①若a>b,则a2>b2;②若a>1,则(a-1)0=1;③两个全等三角形的面积相等.其中原命题与逆命题均为真命题的个数是( )
A.0 B.3 C.2 D.1
5.△ABC的三边长分别为a,b,c.下列条件:①∠A=∠B-∠C;②a∶b∶c=5∶12∶13;③∠A∶∠B∶∠C=3∶4∶5;④a=32,b=42,c=52.其中能判断△ABC是直角三角形的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
6.在△ABC中,a,b,c分别是∠A,∠B,∠C的对边.若(a-1)2+|b-|+=0,则这个三角形一定是 .
7.如图,分别以△ABC的三边为直径向外作3个半圆,它们的面积分别为4π,5π,9π,则△ABC 直角三角形(填“是”或“不是”).
8.观察以下几组勾股数,并寻找规律:①3,4,5;②5,12,13;③7,24,25;④9,40,41;…请你写出具有以上规律的第⑥组勾股数: .
9.命题“如果a+b=0,那么a,b互为相反数”的逆命题为 .
10.如图,在四边形ABCD中,AB=AD=4,∠A=60°,BC=4,CD=8,则∠ADC= °.
11.如图,网格中的每个小正方形的边长都是1,A,B,C三点是小正方形的顶点,则∠ABC的度数为 .
12.如图所示的网格是正方形网格,则∠PAB+∠PBA= °(点A,B,P是网格线交点).
三、解答题
13.在△ABC中,已知a=2n,b=n2-1,c=n2+1(n>1),试判断△ABC的形状,并说明理由.
14.写出下列各命题的逆命题,
并判断逆命题的真假性.
(1)两直线平行,同位角相等;
(2)全等三角形的对应角相等;
(3)线段垂直平分线上的点到线段的两个端点的距
离相等;
(4)如果a是偶数,那么2a是偶数.
15.如图,已知AD是△ABC的中线,DE⊥AC于点E,CE=1,DE=2,AE=4.
(1)求AD的长;
(2)求证:AD垂直平分线段BC.
16.如图,在△ABC中,AC=8,BC=6,以AB为边向外作△ABE,DE为AB边上的高,DE=12,S△ABE=60,求∠C的度数.
17.阅读:能够成为直角三角形三条边长的三个正整数a,b,c称为勾股数.世界上第一次给出勾股数通解公式的是我国古代数学著作《九章算术》,其勾股数组公式为其中m>n>0,m,n是互质的奇数.
应用:当n=1时,求有一边长为5的直角三角形的另外两条边长.
7
参考答案
一、选择题
1.下列各组数中,不能作为直角三角形三边长的是( B )
A.3,4,5 B.4,5,6
C.6,8,10 D.5,12,13
2.如果三角形的三边长分别为,,2,那么这个三角形的最大内角的度数为( D )
A.30° B.45° C.60° D.90°
3.下列各组数中,是勾股数的是( D )
A.,, B.,,
C.0.3,0.4,0.5 D.25,60,65
4.已知下列命题:①若a>b,则a2>b2;②若a>1,则(a-1)0=1;③两个全等三角形的面积相等.其中原命题与逆命题均为真命题的个数是( A )
A.0 B.3 C.2 D.1
5.△ABC的三边长分别为a,b,c.下列条件:①∠A=∠B-∠C;②a∶b∶c=5∶12∶13;③∠A∶∠B∶∠C=3∶4∶5;④a=32,b=42,c=52.其中能判断△ABC是直角三角形的有( B )
A.1个 B.2个 C.3个 D.4个
二、填空题
6.在△ABC中,a,b,c分别是∠A,∠B,∠C的对边.若(a-1)2+|b-|+=0,则这个三角形一定是 .
【答案】直角三角形
7.如图,分别以△ABC的三边为直径向外作3个半圆,它们的面积分别为4π,5π,9π,则△ABC 直角三角形(填“是”或“不是”).
【答案】是
8.观察以下几组勾股数,并寻找规律:①3,4,5;②5,12,13;③7,24,25;④9,40,41;…请你写出具有以上规律的第⑥组勾股数: .
【答案】13,84,85
9.命题“如果a+b=0,那么a,b互为相反数”的逆命题为 .
【答案】如果a,b互为相反数,那么a+b=0
10.如图,在四边形ABCD中,AB=AD=4,∠A=60°,BC=4,CD=8,则∠ADC= °.
【答案】150
11.如图,网格中的每个小正方形的边长都是1,A,B,C三点是小正方形的顶点,则∠ABC的度数为 .
【答案】45°
12.如图所示的网格是正方形网格,则∠PAB+∠PBA= °(点A,B,P是网格线交点).
【解析】如图,延长AP交格点于D,连接BD,则PD2=BD2=12+22=5,PB2=12+32=10,
∴PD2+DB2=PB2.
∴∠PDB=90°.
∴∠DPB=∠PAB+∠PBA=45°.故答案为45.
三、解答题
13.在△ABC中,已知a=2n,b=n2-1,c=n2+1(n>1),试判断△ABC的形状,并说明理由.
解:△ABC是直角三角形.理由如下:
∵a=2n,b=n2-1,c=n2+1(n>1),
∴a2+b2=(2n)2+(n2-1)2=n4+2n2+1,c2=(n2+1)2=n4+2n2+1.
∴a2+b2=c2.
∴△ABC是直角三角形.
14.写出下列各命题的逆命题,
并判断逆命题的真假性.
(1)两直线平行,同位角相等;
(2)全等三角形的对应角相等;
(3)线段垂直平分线上的点到线段的两个端点的距
离相等;
(4)如果a是偶数,那么2a是偶数.
解:(1)同位角相等,两直线平行.真命题.
(2)对应角相等的三角形全等.假命题.
(3)到线段的两个端点的距离相等的点在线段的垂直平分线上.真命题.
(4)如果2a是偶数,那么a是偶数.假命题.
15.如图,已知AD是△ABC的中线,DE⊥AC于点E,CE=1,DE=2,AE=4.
(1)求AD的长;
(1)解:∵DE⊥AC于点E,
∴∠AED=90°.
在Rt△ADE中,AD2=AE2+DE2=42+22=20,
∴AD=2.
(2)求证:AD垂直平分线段BC.
(2)证明:在Rt△ADE中,∠AED=90°,
∴AD2=AE2+DE2=42+22=20.
同理CD2=5,∴AD2+CD2=25.
∵AC=AE+CE=4+1=5,∴AC2=25.
∴AD2+CD2=AC2.∴△ADC是直角三角形.
∴∠ADC=90°.
∵AD是△ABC的中线,∴AD垂直平分线段BC.
16.如图,在△ABC中,AC=8,BC=6,以AB为边向外作△ABE,DE为AB边上的高,DE=12,S△ABE=60,求∠C的度数.
解:∵DE=12,S△ABE=DE·AB=60,∴AB=10.
∵AC=8,BC=6,82+62=102,
∴AC2+BC2=AB2.
由勾股定理的逆定理得∠C=90°.
17.阅读:能够成为直角三角形三条边长的三个正整数a,b,c称为勾股数.世界上第一次给出勾股数通解公式的是我国古代数学著作《九章算术》,其勾股数组公式为其中m>n>0,m,n是互质的奇数.
应用:当n=1时,求有一边长为5的直角三角形的另外两条边长.
解:当n=1时,a=(m2-1)①,b=m②,c=(m2+1)③.
∵直角三角形有一边长为5,
当a=5时,(m2-1)=5,
解得m=±(舍去);
当b=5时,即m=5,代入①③得a=12,c=13;
当c=5时,(m2+1)=5,解得m=±3.
∵m>0,∴m=3.
代入①②得a=4,b=3.
综上所述,直角三角形的另外两条边长分别为12,13或3,4.
17.2 勾股定理的逆定理
第1课时 勾股定理的逆定理
一、选择题
1.下列各组数中,不能作为直角三角形三边长的是( )
A.3,4,5 B.4,5,6
C.6,8,10 D.5,12,13
2.如果三角形的三边长分别为,,2,那么这个三角形的最大内角的度数为( )
A.30° B.45° C.60° D.90°
3.下列各组数中,是勾股数的是( )
A.,, B.,,
C.0.3,0.4,0.5 D.25,60,65
4.已知下列命题:①若a>b,则a2>b2;②若a>1,则(a-1)0=1;③两个全等三角形的面积相等.其中原命题与逆命题均为真命题的个数是( )
A.0 B.3 C.2 D.1
5.△ABC的三边长分别为a,b,c.下列条件:①∠A=∠B-∠C;②a∶b∶c=5∶12∶13;③∠A∶∠B∶∠C=3∶4∶5;④a=32,b=42,c=52.其中能判断△ABC是直角三角形的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
6.在△ABC中,a,b,c分别是∠A,∠B,∠C的对边.若(a-1)2+|b-|+=0,则这个三角形一定是 .
7.如图,分别以△ABC的三边为直径向外作3个半圆,它们的面积分别为4π,5π,9π,则△ABC 直角三角形(填“是”或“不是”).
8.观察以下几组勾股数,并寻找规律:①3,4,5;②5,12,13;③7,24,25;④9,40,41;…请你写出具有以上规律的第⑥组勾股数: .
9.命题“如果a+b=0,那么a,b互为相反数”的逆命题为 .
10.如图,在四边形ABCD中,AB=AD=4,∠A=60°,BC=4,CD=8,则∠ADC= °.
11.如图,网格中的每个小正方形的边长都是1,A,B,C三点是小正方形的顶点,则∠ABC的度数为 .
12.如图所示的网格是正方形网格,则∠PAB+∠PBA= °(点A,B,P是网格线交点).
三、解答题
13.在△ABC中,已知a=2n,b=n2-1,c=n2+1(n>1),试判断△ABC的形状,并说明理由.
14.写出下列各命题的逆命题,
并判断逆命题的真假性.
(1)两直线平行,同位角相等;
(2)全等三角形的对应角相等;
(3)线段垂直平分线上的点到线段的两个端点的距
离相等;
(4)如果a是偶数,那么2a是偶数.
15.如图,已知AD是△ABC的中线,DE⊥AC于点E,CE=1,DE=2,AE=4.
(1)求AD的长;
(2)求证:AD垂直平分线段BC.
16.如图,在△ABC中,AC=8,BC=6,以AB为边向外作△ABE,DE为AB边上的高,DE=12,S△ABE=60,求∠C的度数.
17.阅读:能够成为直角三角形三条边长的三个正整数a,b,c称为勾股数.世界上第一次给出勾股数通解公式的是我国古代数学著作《九章算术》,其勾股数组公式为其中m>n>0,m,n是互质的奇数.
应用:当n=1时,求有一边长为5的直角三角形的另外两条边长.
7
参考答案
一、选择题
1.下列各组数中,不能作为直角三角形三边长的是( B )
A.3,4,5 B.4,5,6
C.6,8,10 D.5,12,13
2.如果三角形的三边长分别为,,2,那么这个三角形的最大内角的度数为( D )
A.30° B.45° C.60° D.90°
3.下列各组数中,是勾股数的是( D )
A.,, B.,,
C.0.3,0.4,0.5 D.25,60,65
4.已知下列命题:①若a>b,则a2>b2;②若a>1,则(a-1)0=1;③两个全等三角形的面积相等.其中原命题与逆命题均为真命题的个数是( A )
A.0 B.3 C.2 D.1
5.△ABC的三边长分别为a,b,c.下列条件:①∠A=∠B-∠C;②a∶b∶c=5∶12∶13;③∠A∶∠B∶∠C=3∶4∶5;④a=32,b=42,c=52.其中能判断△ABC是直角三角形的有( B )
A.1个 B.2个 C.3个 D.4个
二、填空题
6.在△ABC中,a,b,c分别是∠A,∠B,∠C的对边.若(a-1)2+|b-|+=0,则这个三角形一定是 .
【答案】直角三角形
7.如图,分别以△ABC的三边为直径向外作3个半圆,它们的面积分别为4π,5π,9π,则△ABC 直角三角形(填“是”或“不是”).
【答案】是
8.观察以下几组勾股数,并寻找规律:①3,4,5;②5,12,13;③7,24,25;④9,40,41;…请你写出具有以上规律的第⑥组勾股数: .
【答案】13,84,85
9.命题“如果a+b=0,那么a,b互为相反数”的逆命题为 .
【答案】如果a,b互为相反数,那么a+b=0
10.如图,在四边形ABCD中,AB=AD=4,∠A=60°,BC=4,CD=8,则∠ADC= °.
【答案】150
11.如图,网格中的每个小正方形的边长都是1,A,B,C三点是小正方形的顶点,则∠ABC的度数为 .
【答案】45°
12.如图所示的网格是正方形网格,则∠PAB+∠PBA= °(点A,B,P是网格线交点).
【解析】如图,延长AP交格点于D,连接BD,则PD2=BD2=12+22=5,PB2=12+32=10,
∴PD2+DB2=PB2.
∴∠PDB=90°.
∴∠DPB=∠PAB+∠PBA=45°.故答案为45.
三、解答题
13.在△ABC中,已知a=2n,b=n2-1,c=n2+1(n>1),试判断△ABC的形状,并说明理由.
解:△ABC是直角三角形.理由如下:
∵a=2n,b=n2-1,c=n2+1(n>1),
∴a2+b2=(2n)2+(n2-1)2=n4+2n2+1,c2=(n2+1)2=n4+2n2+1.
∴a2+b2=c2.
∴△ABC是直角三角形.
14.写出下列各命题的逆命题,
并判断逆命题的真假性.
(1)两直线平行,同位角相等;
(2)全等三角形的对应角相等;
(3)线段垂直平分线上的点到线段的两个端点的距
离相等;
(4)如果a是偶数,那么2a是偶数.
解:(1)同位角相等,两直线平行.真命题.
(2)对应角相等的三角形全等.假命题.
(3)到线段的两个端点的距离相等的点在线段的垂直平分线上.真命题.
(4)如果2a是偶数,那么a是偶数.假命题.
15.如图,已知AD是△ABC的中线,DE⊥AC于点E,CE=1,DE=2,AE=4.
(1)求AD的长;
(1)解:∵DE⊥AC于点E,
∴∠AED=90°.
在Rt△ADE中,AD2=AE2+DE2=42+22=20,
∴AD=2.
(2)求证:AD垂直平分线段BC.
(2)证明:在Rt△ADE中,∠AED=90°,
∴AD2=AE2+DE2=42+22=20.
同理CD2=5,∴AD2+CD2=25.
∵AC=AE+CE=4+1=5,∴AC2=25.
∴AD2+CD2=AC2.∴△ADC是直角三角形.
∴∠ADC=90°.
∵AD是△ABC的中线,∴AD垂直平分线段BC.
16.如图,在△ABC中,AC=8,BC=6,以AB为边向外作△ABE,DE为AB边上的高,DE=12,S△ABE=60,求∠C的度数.
解:∵DE=12,S△ABE=DE·AB=60,∴AB=10.
∵AC=8,BC=6,82+62=102,
∴AC2+BC2=AB2.
由勾股定理的逆定理得∠C=90°.
17.阅读:能够成为直角三角形三条边长的三个正整数a,b,c称为勾股数.世界上第一次给出勾股数通解公式的是我国古代数学著作《九章算术》,其勾股数组公式为其中m>n>0,m,n是互质的奇数.
应用:当n=1时,求有一边长为5的直角三角形的另外两条边长.
解:当n=1时,a=(m2-1)①,b=m②,c=(m2+1)③.
∵直角三角形有一边长为5,
当a=5时,(m2-1)=5,
解得m=±(舍去);
当b=5时,即m=5,代入①③得a=12,c=13;
当c=5时,(m2+1)=5,解得m=±3.
∵m>0,∴m=3.
代入①②得a=4,b=3.
综上所述,直角三角形的另外两条边长分别为12,13或3,4.
