19[1].2.1矩形的性质
文档属性
| 名称 | 19[1].2.1矩形的性质 |

|
|
| 格式 | rar | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-04-28 00:00:00 | ||
图片预览



文档简介
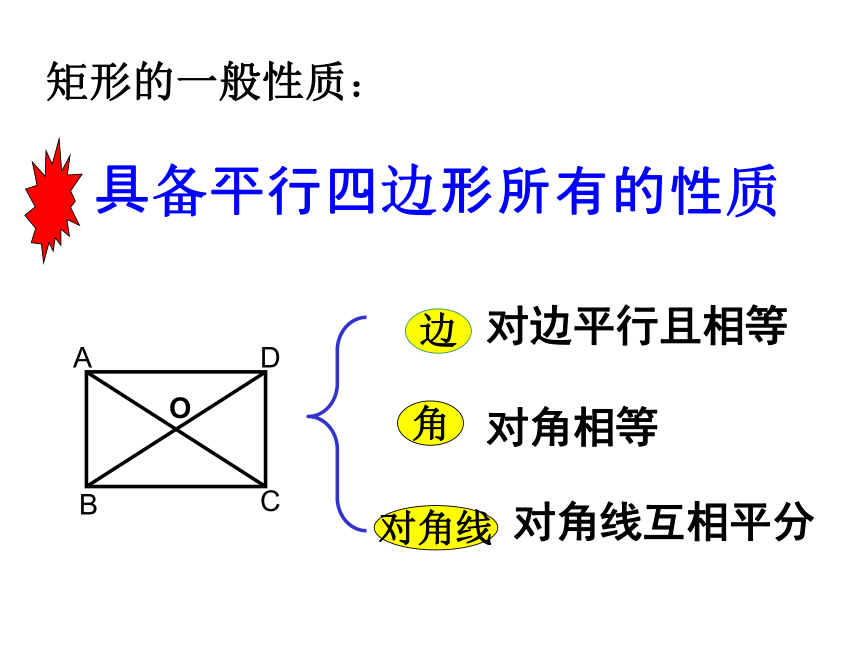
课件41张PPT。19.2 特殊的平行四边形19.2.1 矩形有一个角是直角的平行四边形是矩形矩形的定义:对边平行且相等对角相等对角线互相平分矩形的一般性质:探索新知:
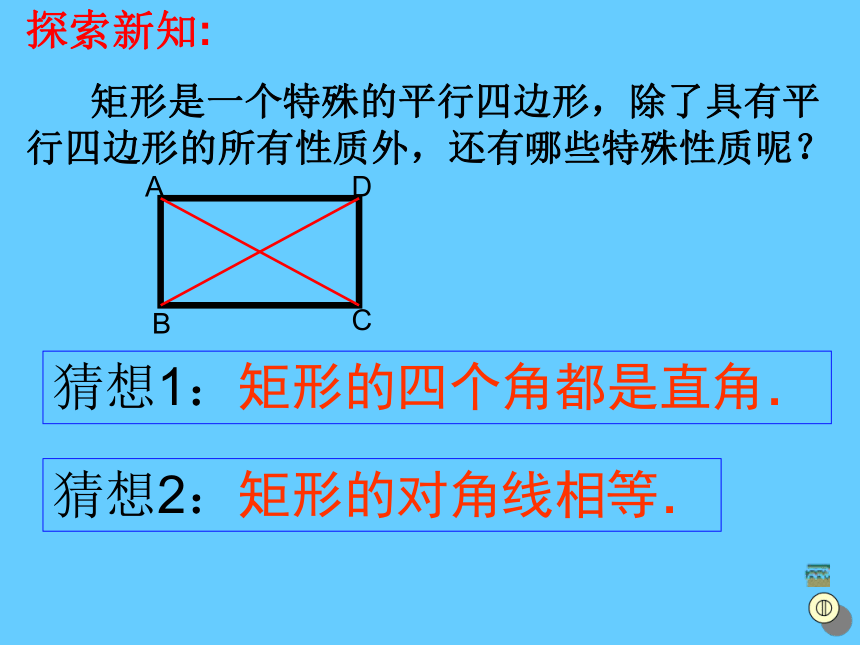
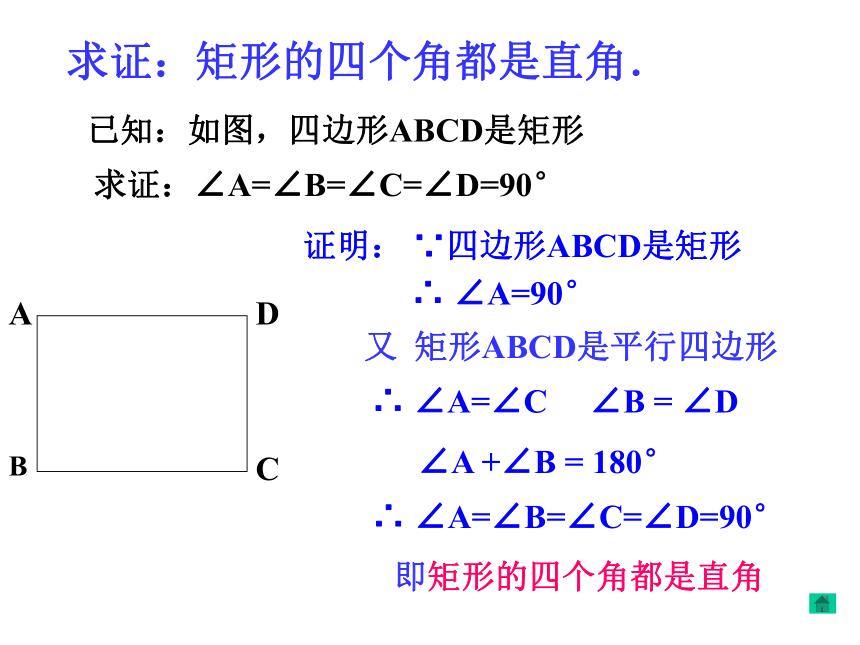
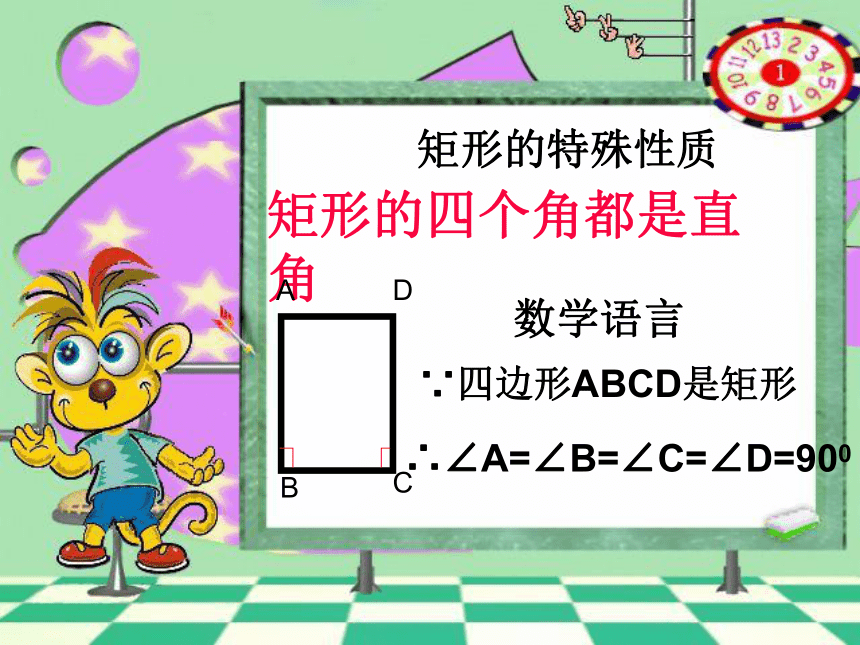
矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?猜想1:矩形的四个角都是直角.猜想2:矩形的对角线相等.ABCD矩形特殊的性质矩形的四个角都是直角.矩形的两条对角线相等.从角上看:从对角线上看:求证:矩形的四个角都是直角.已知:如图,四边形ABCD是矩形求证:∠A=∠B=∠C=∠D=90°证明: ∵四边形ABCD是矩形∴ ∠A=90°又 矩形ABCD是平行四边形∴ ∠A=∠C ∠B = ∠D
∠A +∠B = 180°∴ ∠A=∠B=∠C=∠D=90°
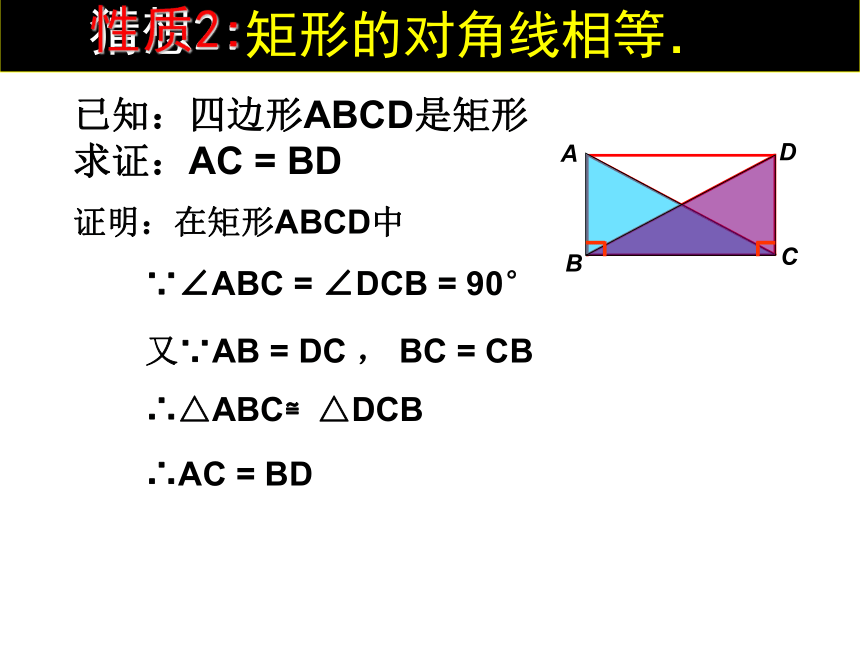
即矩形的四个角都是直角已知:四边形ABCD是矩形
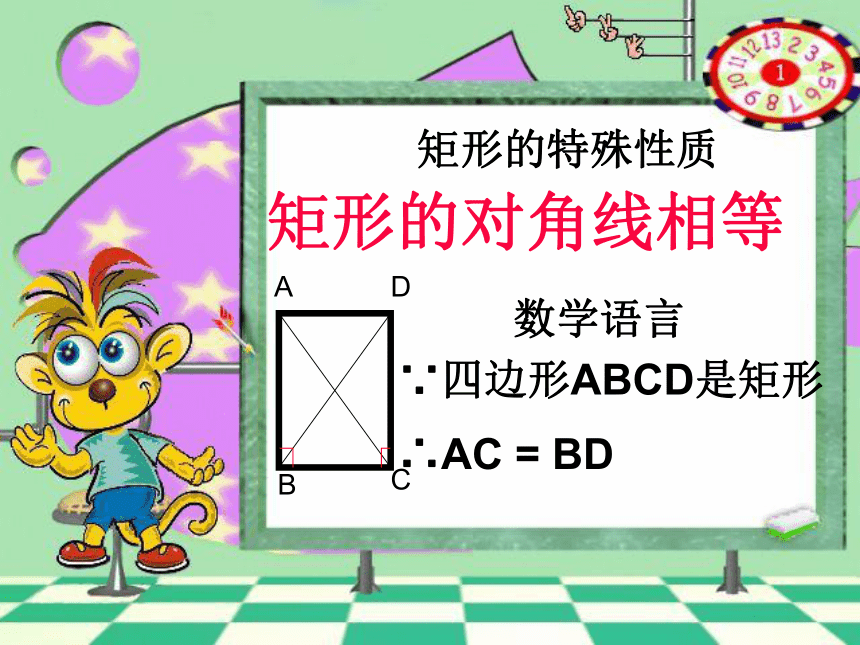
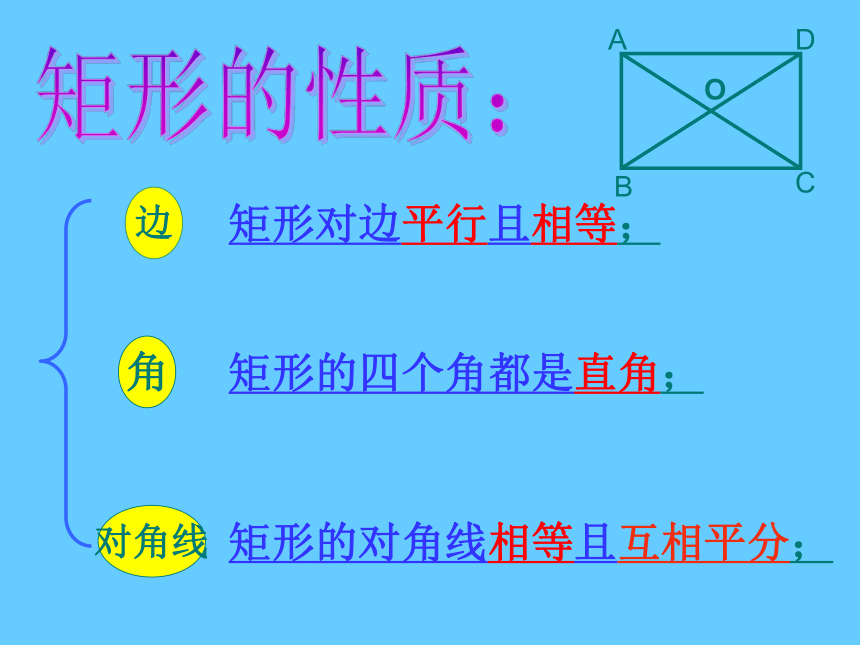
求证:AC = BD证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°又∵AB = DC , BC = CB∴△ABC≌△DCB∴AC = BD 矩形的对角线相等.猜想2:性质2:矩形的特殊性质矩形的四个角都是直角数学语言∵四边形ABCD是矩形 ∴∠A=∠B=∠C=∠D=900矩形的特殊性质矩形的对角线相等数学语言∵四边形ABCD是矩形 ∴AC = BD边对角线角矩形的性质:矩形对边平行且相等;矩形的四个角都是直角;矩形的对角线相等且互相平分;思维提升既是中心对称图形又是轴对称图形对边平行且
相等四个角都等于
90°对角线互相
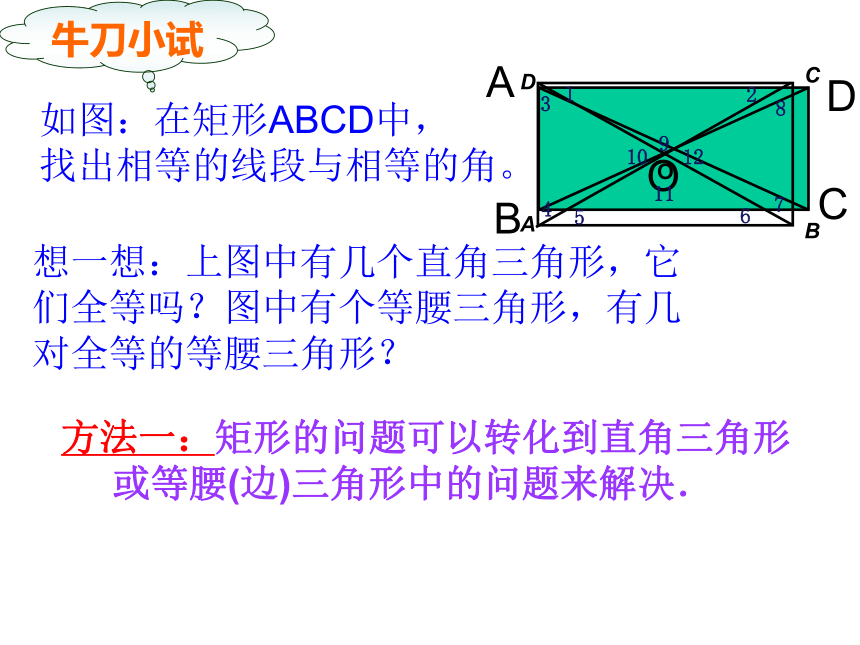
平分且相等如图:在矩形ABCD中, 找出相等的线段与相等的角。想一想:上图中有几个直角三角形,它们全等吗?图中有个等腰三角形,有几对全等的等腰三角形?牛刀小试方法一:矩形的问题可以转化到直角三角形或等腰(边)三角形中的问题来解决. 例题:解:∵四边形ABCD是矩形,
∴AC=BD(矩形的对角线相等).又∵OA=OC= AC, OB=OD= BD,∴OA=OD∵∠AOD=120 ° ,∴ ∠ ODA= ∠OAD= =30°,又 ∵∠DAB=90°(矩形的四个角都是直角).
∴BD=2AB=2×4=8 ( cm ) .如图:四边形ABCD是矩形
若已知AB=8㎝,AD=6㎝,
则AC= ㎝ , OB= ㎝.
2 若OA=3㎝,则AC= ㎝.
若已知AC=10㎝,BC=6㎝,则矩形的周长= ㎝,
矩形的面积= ㎝2.
4 若已知 ∠DOC=120°,AD=6㎝,则AC= ㎝.51012482861.矩形具有而平行四边形不具有的性
质( )
(A)内角和是360度
(B)对角相等
(C)对边平行且相等
(D)对角线相等 2.下面性质中,矩形不一定具有的是( )
(A)对角线相等
(B)四个角相等
(C)是轴对称图形
(D)对角线垂直3.矩形ABCD中,∠ABD:∠DBC=2:1,
则∠ADB=?????????? 度。若AB=4,则AC=???? 。 ?????????????????????????????????????答案
恭喜!可直接获得一颗星!!!5.如图,矩形ABCD,AE⊥BD,垂足为E,∠DAE=2 ∠BAE。求∠BAE和∠DAE的度数。6.矩形的边长为10cm和15cm,其中一个
内角的平分线分长边为两部分,这两部
分分别为???? cm,????? cm. ?????????????????????????????????E7.如果矩形的一边与对角线的夹角为50o,
则两对角线相交所成的锐角的度数为?? ??????????。??????????? ???????????????????????????????????????????????????????????????????? ? 答案5008.已知:在矩形ABCD中,E为BC上一点,∠EAD=∠EDA
求证:E为BC中点.
OABCD公平,因为OA=OC=OB=OD生活链接---投圈游戏ABCO得到:直角三角形的一个性质
直角三角形斜边上的中线等于斜边的一半.数学语言: ∵在Rt△ABC中, BO是斜边AC上的中线
∴ BO= AC在Rt△ABC中, BO= AC探索新知已知:在△ABC中∠ACB=90°,AD = BD证明:延长CD到E使DE=CD,连 结AE、BE.∵AD = BD ,CD = EDE∴ACBE是平行四边形又∵∠ACB = 90∴CE = AB由于CD= CE
∴ CD = AB求证:CD = AB 某学校因地制宜:先向北量6m,再向东量8m,接着向南量6m,最后向西量8m,在圈出的这块空地上建一个草坪.(1)圈出的空地是什么形状? (2)考虑到护理草坪,学校购置了一台自动喷水器, 这台机器的最大喷水距离为5m,问这台机器能对整个草坪进行护理吗?若能,则喷水器应安放在何处;若不能,请说明理由.O6868例1:如图,已知在Rt△ABC中,∠ACB=90°,D、E、F分别是AB、AC、BC的中点,求证CD=EF1、如图,已知在△ABC中,D、E、F分别是BC 、 AC、 AB的中点,AH⊥BC于H,DF=8,则EH=_____BCAHDFE2、如图,已知在△ABC中,CE、BD分别是AB、AC上的高线,F、G分别是DE、 AC的中点,求证FG⊥DE
ABCDEFG例2: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长?方法小结: 如果矩形两对角 线的夹角是60°
或120°, 则其中必有等边三角形. ∴AC与BD相等且互相平分∴ OA=OB∵ ∠AOB=60°∴ △AOB是等边三角形∴ OA=AB=4(㎝)∴ 矩形的对角线长 AC=BD=2OA=8(㎝)解:∵ 四边形ABCD是矩形练习 已知:矩形ABCD的两条对角线相交与O,∠AOD=120°,AD = 4 cm.
求矩形对角线的长∴BD = 2AB解:∵四边形ABCD是矩形∴OA = OD( )∵ ∠AOD=120°∴ ∠1=30°又∵ ∠ABC=90°( )矩形的对角线相等且平分矩形的每个内角都是直角成长快乐训练营点击进入 矩形具有而一般平行四边形不
具有的性质是 ( ) B.对边相等C营中热身已知:四边形ABCD是矩形
1.若已知AB=8㎝,AD=6㎝,
则AC=_______ ㎝ OB=_______ ㎝
2.若已知 ∠DOC=120°,AC=8㎝,则AD= _____cm
AB= _____cm5104营中寻宝3.已知△ABC是Rt△,∠ABC=900,
BD是斜边AC上的中线(1)若BD=3㎝ 则AC= ㎝
(2) 若∠C=30°,AB=5㎝,则AC=
BD= ㎝.6510营中寻宝例3:如图,把矩形ABCD沿直线BD折叠,使点C落在C’处,BC’交AD于点E,求点E到BD的距离ABCDEC’例4:如图,在矩形ABCD中,E为BC上的一点,且DE=BC,AF⊥DE于点F,求证EF=BEABCDEF本课小结矩形的四个角都是直角.※ 矩形的性质定理1矩形的对角线相等.※ 矩形的性质定理2※ 直角三角形的一个性质 直角三角形斜边上的中线等于斜边的一半.反思拓展:1、工人师傅做铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料(如图1),使
AB=CD, EF=GH;
(2)摆放成如图(2)的四边形,则这时窗框的形状是
_____,根据的数学道理是__________;
(3)将直角尺靠紧窗框的一个角(如图3)调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图4),说明窗框合格,这时窗框是____,根据的数学道理是________________。平行四边形两组对边分别相等的四边形是平行四边形矩形有一个角是直角的平行四边形是矩形再见脸蛋方方是矩形,例如黑板和窗门。对角线段皆相等,相互交叉且平分。内有直角三角形,斜边中线半斜边。若要牢记其定义,直角平行四边形。矩形之歌
矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?猜想1:矩形的四个角都是直角.猜想2:矩形的对角线相等.ABCD矩形特殊的性质矩形的四个角都是直角.矩形的两条对角线相等.从角上看:从对角线上看:求证:矩形的四个角都是直角.已知:如图,四边形ABCD是矩形求证:∠A=∠B=∠C=∠D=90°证明: ∵四边形ABCD是矩形∴ ∠A=90°又 矩形ABCD是平行四边形∴ ∠A=∠C ∠B = ∠D
∠A +∠B = 180°∴ ∠A=∠B=∠C=∠D=90°
即矩形的四个角都是直角已知:四边形ABCD是矩形
求证:AC = BD证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°又∵AB = DC , BC = CB∴△ABC≌△DCB∴AC = BD 矩形的对角线相等.猜想2:性质2:矩形的特殊性质矩形的四个角都是直角数学语言∵四边形ABCD是矩形 ∴∠A=∠B=∠C=∠D=900矩形的特殊性质矩形的对角线相等数学语言∵四边形ABCD是矩形 ∴AC = BD边对角线角矩形的性质:矩形对边平行且相等;矩形的四个角都是直角;矩形的对角线相等且互相平分;思维提升既是中心对称图形又是轴对称图形对边平行且
相等四个角都等于
90°对角线互相
平分且相等如图:在矩形ABCD中, 找出相等的线段与相等的角。想一想:上图中有几个直角三角形,它们全等吗?图中有个等腰三角形,有几对全等的等腰三角形?牛刀小试方法一:矩形的问题可以转化到直角三角形或等腰(边)三角形中的问题来解决. 例题:解:∵四边形ABCD是矩形,
∴AC=BD(矩形的对角线相等).又∵OA=OC= AC, OB=OD= BD,∴OA=OD∵∠AOD=120 ° ,∴ ∠ ODA= ∠OAD= =30°,又 ∵∠DAB=90°(矩形的四个角都是直角).
∴BD=2AB=2×4=8 ( cm ) .如图:四边形ABCD是矩形
若已知AB=8㎝,AD=6㎝,
则AC= ㎝ , OB= ㎝.
2 若OA=3㎝,则AC= ㎝.
若已知AC=10㎝,BC=6㎝,则矩形的周长= ㎝,
矩形的面积= ㎝2.
4 若已知 ∠DOC=120°,AD=6㎝,则AC= ㎝.51012482861.矩形具有而平行四边形不具有的性
质( )
(A)内角和是360度
(B)对角相等
(C)对边平行且相等
(D)对角线相等 2.下面性质中,矩形不一定具有的是( )
(A)对角线相等
(B)四个角相等
(C)是轴对称图形
(D)对角线垂直3.矩形ABCD中,∠ABD:∠DBC=2:1,
则∠ADB=?????????? 度。若AB=4,则AC=???? 。 ?????????????????????????????????????答案
恭喜!可直接获得一颗星!!!5.如图,矩形ABCD,AE⊥BD,垂足为E,∠DAE=2 ∠BAE。求∠BAE和∠DAE的度数。6.矩形的边长为10cm和15cm,其中一个
内角的平分线分长边为两部分,这两部
分分别为???? cm,????? cm. ?????????????????????????????????E7.如果矩形的一边与对角线的夹角为50o,
则两对角线相交所成的锐角的度数为?? ??????????。??????????? ???????????????????????????????????????????????????????????????????? ? 答案5008.已知:在矩形ABCD中,E为BC上一点,∠EAD=∠EDA
求证:E为BC中点.
OABCD公平,因为OA=OC=OB=OD生活链接---投圈游戏ABCO得到:直角三角形的一个性质
直角三角形斜边上的中线等于斜边的一半.数学语言: ∵在Rt△ABC中, BO是斜边AC上的中线
∴ BO= AC在Rt△ABC中, BO= AC探索新知已知:在△ABC中∠ACB=90°,AD = BD证明:延长CD到E使DE=CD,连 结AE、BE.∵AD = BD ,CD = EDE∴ACBE是平行四边形又∵∠ACB = 90∴CE = AB由于CD= CE
∴ CD = AB求证:CD = AB 某学校因地制宜:先向北量6m,再向东量8m,接着向南量6m,最后向西量8m,在圈出的这块空地上建一个草坪.(1)圈出的空地是什么形状? (2)考虑到护理草坪,学校购置了一台自动喷水器, 这台机器的最大喷水距离为5m,问这台机器能对整个草坪进行护理吗?若能,则喷水器应安放在何处;若不能,请说明理由.O6868例1:如图,已知在Rt△ABC中,∠ACB=90°,D、E、F分别是AB、AC、BC的中点,求证CD=EF1、如图,已知在△ABC中,D、E、F分别是BC 、 AC、 AB的中点,AH⊥BC于H,DF=8,则EH=_____BCAHDFE2、如图,已知在△ABC中,CE、BD分别是AB、AC上的高线,F、G分别是DE、 AC的中点,求证FG⊥DE
ABCDEFG例2: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长?方法小结: 如果矩形两对角 线的夹角是60°
或120°, 则其中必有等边三角形. ∴AC与BD相等且互相平分∴ OA=OB∵ ∠AOB=60°∴ △AOB是等边三角形∴ OA=AB=4(㎝)∴ 矩形的对角线长 AC=BD=2OA=8(㎝)解:∵ 四边形ABCD是矩形练习 已知:矩形ABCD的两条对角线相交与O,∠AOD=120°,AD = 4 cm.
求矩形对角线的长∴BD = 2AB解:∵四边形ABCD是矩形∴OA = OD( )∵ ∠AOD=120°∴ ∠1=30°又∵ ∠ABC=90°( )矩形的对角线相等且平分矩形的每个内角都是直角成长快乐训练营点击进入 矩形具有而一般平行四边形不
具有的性质是 ( ) B.对边相等C营中热身已知:四边形ABCD是矩形
1.若已知AB=8㎝,AD=6㎝,
则AC=_______ ㎝ OB=_______ ㎝
2.若已知 ∠DOC=120°,AC=8㎝,则AD= _____cm
AB= _____cm5104营中寻宝3.已知△ABC是Rt△,∠ABC=900,
BD是斜边AC上的中线(1)若BD=3㎝ 则AC= ㎝
(2) 若∠C=30°,AB=5㎝,则AC=
BD= ㎝.6510营中寻宝例3:如图,把矩形ABCD沿直线BD折叠,使点C落在C’处,BC’交AD于点E,求点E到BD的距离ABCDEC’例4:如图,在矩形ABCD中,E为BC上的一点,且DE=BC,AF⊥DE于点F,求证EF=BEABCDEF本课小结矩形的四个角都是直角.※ 矩形的性质定理1矩形的对角线相等.※ 矩形的性质定理2※ 直角三角形的一个性质 直角三角形斜边上的中线等于斜边的一半.反思拓展:1、工人师傅做铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料(如图1),使
AB=CD, EF=GH;
(2)摆放成如图(2)的四边形,则这时窗框的形状是
_____,根据的数学道理是__________;
(3)将直角尺靠紧窗框的一个角(如图3)调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图4),说明窗框合格,这时窗框是____,根据的数学道理是________________。平行四边形两组对边分别相等的四边形是平行四边形矩形有一个角是直角的平行四边形是矩形再见脸蛋方方是矩形,例如黑板和窗门。对角线段皆相等,相互交叉且平分。内有直角三角形,斜边中线半斜边。若要牢记其定义,直角平行四边形。矩形之歌
