内蒙古包头市2024年九年级中考预测卷数学试题(含解析)
文档属性
| 名称 | 内蒙古包头市2024年九年级中考预测卷数学试题(含解析) | 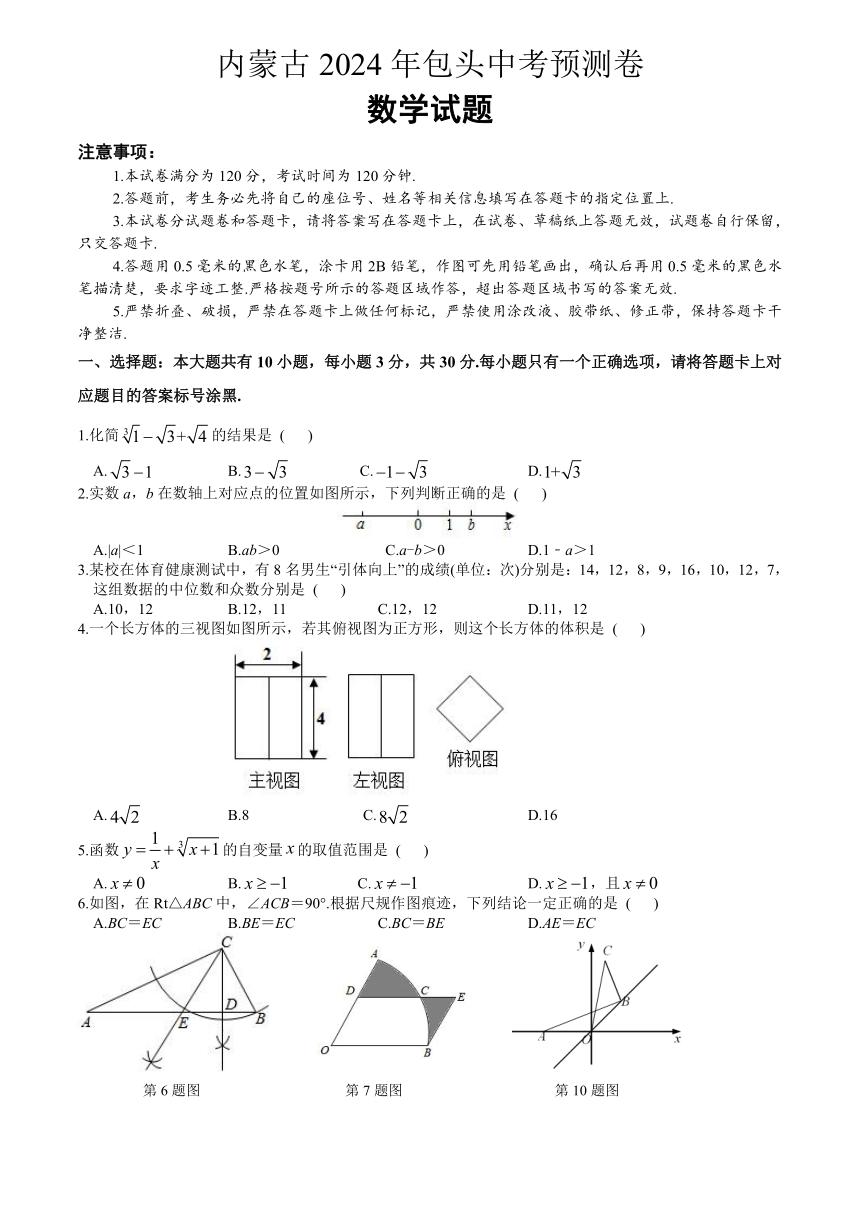 | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-10 17:18:54 | ||
图片预览




文档简介
内蒙古2024年包头中考预测卷
数学试题
注意事项:
1.本试卷满分为120分,考试时间为120分钟.
2.答题前,考生务必先将自己的座位号、姓名等相关信息填写在答题卡的指定位置上.
3.本试卷分试题卷和答题卡,请将答案写在答题卡上,在试卷、草稿纸上答题无效,试题卷自行保留,只交答题卡.
4.答题用0.5毫米的黑色水笔,涂卡用2B铅笔,作图可先用铅笔画出,确认后再用0.5毫米的黑色水笔描清楚,要求字迹工整.严格按题号所示的答题区域作答,超出答题区域书写的答案无效.
5.严禁折叠、破损,严禁在答题卡上做任何标记,严禁使用涂改液、胶带纸、修正带,保持答题卡干净整洁.
一、选择题:本大题共有10小题,每小题3分,共30分.每小题只有一个正确选项,请将答题卡上对应题目的答案标号涂黑.
1.化简的结果是 ( )
A. B. C. D.
2.实数a,b在数轴上对应点的位置如图所示,下列判断正确的是 ( )
A.|a|<1 B.ab>0 C.a-b>0 D.1﹣a>1
3.某校在体育健康测试中,有8名男生“引体向上”的成绩(单位:次)分别是:14,12,8,9,16,10,12,7,这组数据的中位数和众数分别是 ( )
A.10,12 B.12,11 C.12,12 D.11,12
4.一个长方体的三视图如图所示,若其俯视图为正方形,则这个长方体的体积是 ( )
A. B.8 C. D.16
5.函数的自变量的取值范围是 ( )
A. B. C. D.,且
6.如图,在Rt△ABC中,∠ACB=90°.根据尺规作图痕迹,下列结论一定正确的是 ( )
A.BC=EC B.BE=EC C.BC=BE D.AE=EC
第6题图 第7题图 第10题图
7.如图,扇形AOB的圆心角是,半径是,点C为弧AB的中点,过点C作交OA于点D,过点B作交DC延长线于点E,则图中阴影部分面积为 ( )
A. B. C. D.
8.下列命题中:
方程有两个不相等的实数根;
不等式的最大整数解是2;
顺次连接对角线相等的四边形各边中点得到的四边形是矩形;
直角三角形的两条直角边长分别为6和8,则它的外接圆的半径为.
其中是真命题的个数有 ( )
A.1个 B.2个 C.3个 D.4个
9.关于的一元二次方程的两个实数根分别是,,且以,,6为三边的三角形恰好是等腰三角形,则的值为 ( )
A.24 B.25 C.24或25 D.无法确定
10.如图,在平面直角坐标系中,动点A、B分别在x轴上和函数y=x的图像上,AB=4,CB⊥AB,BC=2,则OC的最大值为 ( )
A.2+2 B.2+4 C.2 D.2+2
二、填空题(共6小题,每小题3分,共18分)
11.将59800000用科学记数法表示为__________.
12.若关于的一元一次不等式组的解集是,则的取值范围是______.
13.化简:_________.
14.甲、乙两班举行电脑汉字输入速度比赛,参赛学生每分钟输入汉字的个数经统计计算后结果如下表:
班级 参加人数 中位数 方差 平均数
甲 55 149 191 135
乙 55 151 110 135
某同学根据上表分析得出如下结论:(l)甲、乙两班学生成绩的平均水平相同;(2)乙班优秀(每分钟输入汉字超过150个为优秀)的人数多于甲班优秀的人数;(3)甲班的成绩波动比乙班的成绩波动小、上述结论中正确的是______.(填序号)
15.如图,已知AD是∠BAC的平分线,以线段AB为直径作圆,交∠BAC和角平分线于C,D两点过D向AC作垂线DE垂足为点E,若,则直径________.
第15题图 第16题图
16.如图,双曲线(为常数,)与矩形的边相交于点,与边相交于点,将沿翻折,点恰好落在轴上的点处.则点的坐标为________.
三、解答题:本大题共有7小题,共72分.请将必要的文字说明、计算过程或推理过程写在答题卡的对应位置.
17.(本小题满分6分)计算:.
18.(本小题满分10分)A,B两家酒店规模相当,去年下半年的月盈利折线统计图如图所示.
(1)要评价这两家酒店7~12月的月盈利的平均水平,你选择什么统计量?求出这个统计量;
(2)已知A,B两家酒店7~12月的月盈利的方差分别为1.073(平方万元),0.54(平方万元).根据所给的方差和你在(1)中所求的统计量,结合折线统计图,你认为去年下半年哪家酒店经营状况较好?请简述理由.
(本小题满分10分)如图,我国某海域有,两个港口,相距80海里,港口在港口的东北方向,
点处有一艘货船,该货船在港口的北偏西30°方向,在港口的北偏西75°方向,求货船与港口之间的距离.(结果保留根号)
20.(本小题满分12分)某经销商3月份用18000元购进一批T恤衫售完后,4月份用39000元购进单批相同的T恤衫,数量是3月份的2倍,但每件进价涨了10元.
(1)4月份进了这批T恤衫多少件?
(2)4月份,经销商将这批T恤衫平均分给甲、乙两家分店销售,每件标价180元.甲店按标价卖出a件以后,剩余的按标价八折全部售出;乙店同样按标价卖出a件,然后将b件按标价九折售出,再将剩余的按标价七折全部售出,结果利润与甲店相同.
①用含a的代数式表示b;
②已知乙店按标价售出的数量不超过九折售出的数量,请你求出乙店利润的最大值.
(本小题满分10分)如图,C,D为⊙O上两点,且在直径AB两侧,连结CD交AB于点E,G是上
一点,∠ADC=∠G. (1)求证:∠1=∠2;(2)点C关于DG的对称点为F,连结CF,当点F落在直径AB上时,CF=10,tan∠1=,求⊙O的半径.
22(本小题满分12分)
问题探究:小红遇到这样一个问题:如图1,中,,,AD是中线,求AD的取值范围.她的做法是:延长AD到E,使,连接BE,证明,经过推理和计算使问题得到解决.请回答:
(1)小红证明的判定定理是:________________________;
(2)AD的取值范围是________________________;
方法运用:
(3)如图2,AD是的中线,在AD上取一点F,连结BF并延长交AC于点E,使,求证:.
(4)如图3,在矩形ABCD中,,在BD上取一点F,以BF为斜边作,且,点G是DF的中点,连接EG,CG,求证:.
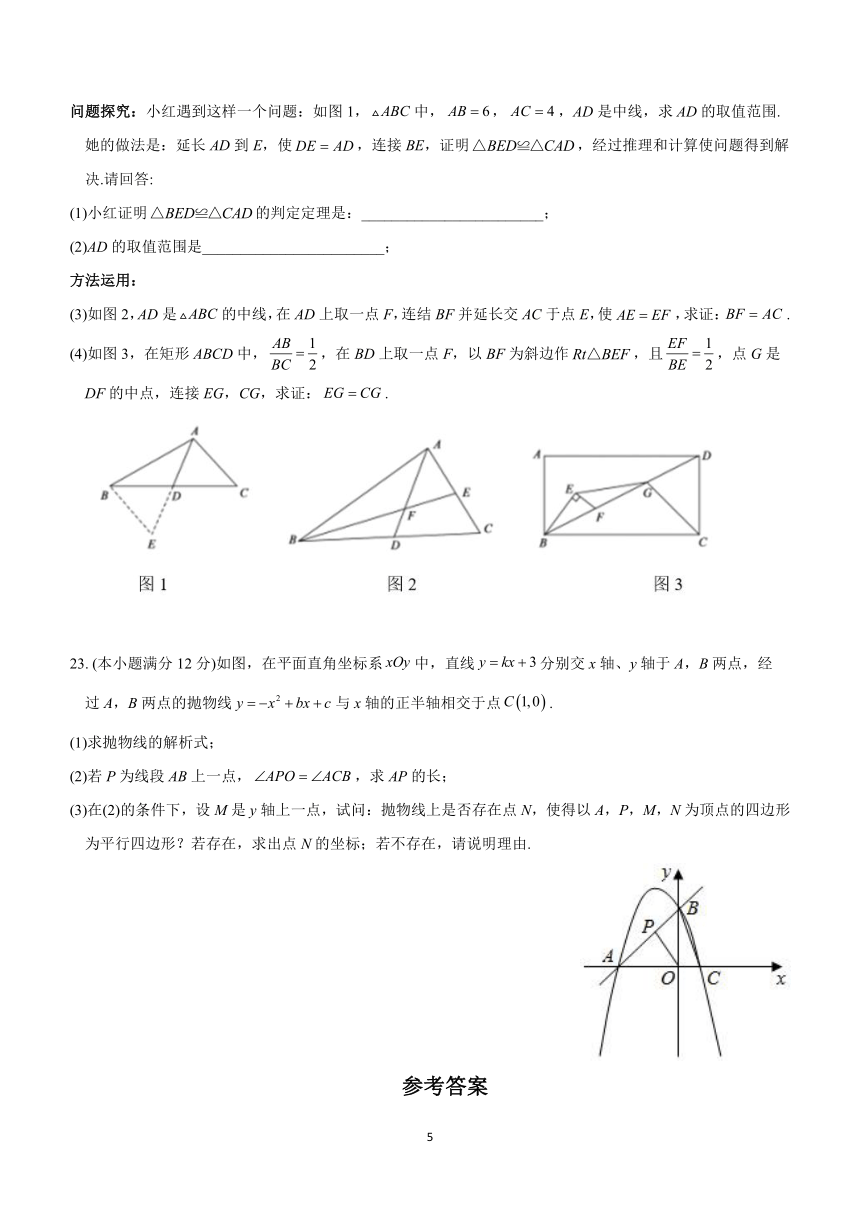
(本小题满分12分)如图,在平面直角坐标系中,直线分别交x轴、y轴于A,B两点,经
过A,B两点的抛物线与x轴的正半轴相交于点.
(1)求抛物线的解析式;
(2)若P为线段AB上一点,,求AP的长;
(3)在(2)的条件下,设M是y轴上一点,试问:抛物线上是否存在点N,使得以A,P,M,N为顶点的四边形为平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.
参考答案
1.B 【解析】原式.故选:B.
2.D 【解析】由数轴上a与1的位置可知:|a|>1,故选项A错误,不符合题意;
因为a<0,b>0,所以ab<0,故选项B错误,不符合题意;
因为a<0,b>0,所以a-b<0,故选项C错误,不符合题意;
因为a<0,所以1 a>1,故选项D正确,符合题意.
故选:D.
3.D 【解析】将这组数据按从小到大的顺序排列如下:7,8,9,10,12,12,14,16.共8个数据,所以第4个和第5个数的平均数是这组数据的中位数,所以中位数为.
∵12出现了2次是出现次数最多的数,
∴众数是12.
故选D.
4.B 【解析】如图,连接AC,BD,交于点O,
由图可知,,
∵四边形ABCD是正方形,
,
,
,
∴长方体的长和宽都是,高为4,
∴长方体的体积为,
故选:B.
5.A 【解析】函数的自变量的取值范围是:,故选A.
6.C 【解析】由作图可知,CD⊥AB,CE平分∠ACD,
∴∠ACE=∠DCE,
∵∠ACB=∠CDB=90°,
∴∠A+∠B=90°,∠B+∠DCB=90°,
∴∠A=∠DCB,
∵∠BEC=∠A+∠ACE,∠BCE=∠ECD+∠DCB,
∴∠BEC=∠BCE,
∴BC=BE,
故选:C.
7.B 【解析】连接,过作交于,作与,
点为弧的中点,
,
,
,
,
,
,
,
,
,
,
,,
四边形是菱形,
,
,
,
,
.
故选:B.
8.A 【解析】方程,,无实数根,错误;
不等式的解集为,最大整数解是1,错误;
顺次连接对角线相等的四边形各边中点得到的四边形是矩形,说法错误,应为菱形;
直角三角形的两条直角边长分别为6和8,则它的外接圆的半径为,正确;
故选:A.
9.C 【解析】①当6为底边时,则,
∴,
∴,
∴方程为,
解得:,
∵,
∴5,5,6能构成等腰三角形;
②当6为腰时,则设,
∴,
∴,
∴方程为,
∴,,
∵,
∴4,6,6能构成等腰三角形;
综上所述:或25.
故选:C.
10.A 【解析】作以B为圆心,以2为半径的圆,
当OC∥AB时最大,此时OC与圆B相切,
过B作BE⊥x轴于E,过A作AD⊥OC于D,
∵BC⊥AB,OC⊥BC,
∴四边形ABCD为矩形,
∴AD=BC=2,CD=AB=4,
点B在y=x上,点A在x轴上,
设A(n,0),B(m,m),
∵∠OAD+∠BAE=90°,∠BAE+∠ABE=90°,
∴∠OAD=∠ABE,
又∠ODA=∠AEB=90°,
∴△AOD∽△BAE,
∴即,
∴
在RtABE中,
AE=m-n,
由勾股定理得:,
,
,
,
,
,
,
,
,
∵2m4,
∴4m216,
,
在Rt△OAD中,
OD=,
,
,
,
,
,
,
∴OD,
OC=OD+DC=,
故选择:A.
11. 【解析】 .
故答案为:.
12. 【解析】解不等式3x-1>x+3,得:x>2,
∵不等式组的解集为,
∴a>2,
故答案为:a>2.
13. 【解析】
.
故答案为:.
14.(1),(2) 【解析】从表中可知,平均字数都是135,(1)正确;
甲班的中位数是149,乙班的中位数是151,比甲的多,而平均数都要为135,说明乙的优秀人数多于甲班的,(2)正确;
甲班的方差大于乙班的,则说明乙班的波动小,所以(3)错误.
(1)(2)正确.
故答案为(1)(2).
15.10 【解析】连接,,,过点作于点,
,,
,
,
是的平分线,,,
,,
,
,
在中,设,则,
,解得:,
.
故答案为:10.
16., 【解析】作轴于,
设,则,
,,
,
,
,,
,
,
,
,
,
,
,.
故答案为,.
17.
【分析】本题主要考查了整式的混合运算、积的乘方、单项式乘单项式等知识点,灵活运用相关运算法则成为解题的关键.根据整式的混合运算法则计算即可.
【解析】
解:
.(6分)
18.【解析】(1)选择两家酒店月营业额的平均数:
,.(5分)
(2)A酒店营业额的平均数比B酒店的营业额的平均数大,且B酒店的营业额的方差小于A酒店,说明B酒店的营业额比较稳定,而从图像上看A酒店的营业额持续稳定增长,潜力大,说明A酒店经营状况好.(10分)
19.22.【解析】过点作于点
根据题意,得,
∵,
∴,
∴,(3分)
在中,
∵,,
∴,
∵,
∴,(6分)
在中
∵,
∴
答:货船与港口之间的距离是海里.(10分)
20.【解析】(1)设3月份购进T恤x件,
由题意得:,解得x=150,
经检验x=150是分式方程的解,符合题意,
∵4月份是3月份数量的2倍,∴4月份购进T恤300件;(4分)
(2)①由题意得,甲店总收入为,
乙店总收入为,
∵甲乙两店利润相等,成本相等,∴总收入也相等,
∴=,
化简可得,∴用含a的代数式表示b为:;(7分)
②乙店利润函数式为,
结合①可得,
∵,,∴,∴=3900,即最大利润为3900元. (10分)
21.【解析】(1)∵∠ADC=∠G,∴,
∵AB为⊙O的直径,∴,
∴,∴,∴∠1=∠2;(3分)
(2)如图,连接OD、FD,
∵,,∴点C、D关于直径AB对称,
∴AB垂直平分CD,∴FC=FD,CE=DE=CD,∠DEB=90°,(6分)
∵点C关于DG的对称点为F,∴DG垂直平分FC,∴FD=CD,
又∵CF=10,∴FC=FD=CD=10,∴DE=CD=5,
∵在Rt△DEB中,tan∠1=,∴,∴,∴BE=2,(8分)
设OB=OD=x,则OE=x–2,
∵在Rt△DOE中,,
∴,解得:,
∴⊙O的半径为.(10分)
22.【解析】(1)如图,AD是中线,
在与中,,
故答案为:.(2分)
(2)
故答案为:.(4分)
(3)证明:延长至点,使,
∵是的中线,∴,
在和中,,
∴,∴,(6分)
又∵,∴,∴,
又∵,∴,∴,
又∵,∴.(8分)
(4)证明:延长至点使,连接、、,
∵G为的中点,∴,
在和中,,
∴,∴,(9分)
在中,∵,∴,
又矩形中,,
∴,∴,∴,(10分)
又,∴,∴,
又为的外角,∴,
即,
∵,
∴,
∴,即,(11分)
在和中,,∴,
又,∴,∴,
∵,
∴,∴是直角三角形,
∵G为的中点,∴,即.(12分)
23.【解析】(1)令,则,∴点B的坐标为(0,3),
抛物线经过点B (0,3),C (1,0),
∴,解得,
∴抛物线的解析式为:;(4分)
(2)令,则,
解得:,
∴点A的坐标为(,0),
∴OA=3,OB=3,OC=1,
,
∵,且,∴△PAO△CAB,
∴,即,∴;(8分)
(3)存在,(9分)
①当AP为平行四边形的边时.
过点P作PD⊥x轴于点D,
∵OA=3,OB=3,∠AOB=,∴∠BAO=∠ABO=,∴△PAD为等腰直角三角形,
∵,∴PD=AD=2,∴点P的坐标为(,2),
当N在AB的上方时,过点N作NE⊥y轴于点E,如图,
∵四边形APMN为平行四边形,∴NM∥AP,NM=AP=,
∴∠NME=∠ABO=,∴△NME为等腰直角三角形,
∴Rt△NMERt△APD,∴NE=AD=2,
当时,,∴点N的坐标为(,3). (10分)
当N在AB的下方时,过点N作NF⊥y轴于点F,如图,
同理可得:Rt△NMFRt△APD,∴NF=AD=2,
当时,,∴点N的坐标为(,).(11分)
②当AP为平行四边形的对角线时,点N的坐标为(–4,).
综上,点N的坐标为(,3) 或(,) 或(–4,).(12分)
数学试题
注意事项:
1.本试卷满分为120分,考试时间为120分钟.
2.答题前,考生务必先将自己的座位号、姓名等相关信息填写在答题卡的指定位置上.
3.本试卷分试题卷和答题卡,请将答案写在答题卡上,在试卷、草稿纸上答题无效,试题卷自行保留,只交答题卡.
4.答题用0.5毫米的黑色水笔,涂卡用2B铅笔,作图可先用铅笔画出,确认后再用0.5毫米的黑色水笔描清楚,要求字迹工整.严格按题号所示的答题区域作答,超出答题区域书写的答案无效.
5.严禁折叠、破损,严禁在答题卡上做任何标记,严禁使用涂改液、胶带纸、修正带,保持答题卡干净整洁.
一、选择题:本大题共有10小题,每小题3分,共30分.每小题只有一个正确选项,请将答题卡上对应题目的答案标号涂黑.
1.化简的结果是 ( )
A. B. C. D.
2.实数a,b在数轴上对应点的位置如图所示,下列判断正确的是 ( )
A.|a|<1 B.ab>0 C.a-b>0 D.1﹣a>1
3.某校在体育健康测试中,有8名男生“引体向上”的成绩(单位:次)分别是:14,12,8,9,16,10,12,7,这组数据的中位数和众数分别是 ( )
A.10,12 B.12,11 C.12,12 D.11,12
4.一个长方体的三视图如图所示,若其俯视图为正方形,则这个长方体的体积是 ( )
A. B.8 C. D.16
5.函数的自变量的取值范围是 ( )
A. B. C. D.,且
6.如图,在Rt△ABC中,∠ACB=90°.根据尺规作图痕迹,下列结论一定正确的是 ( )
A.BC=EC B.BE=EC C.BC=BE D.AE=EC
第6题图 第7题图 第10题图
7.如图,扇形AOB的圆心角是,半径是,点C为弧AB的中点,过点C作交OA于点D,过点B作交DC延长线于点E,则图中阴影部分面积为 ( )
A. B. C. D.
8.下列命题中:
方程有两个不相等的实数根;
不等式的最大整数解是2;
顺次连接对角线相等的四边形各边中点得到的四边形是矩形;
直角三角形的两条直角边长分别为6和8,则它的外接圆的半径为.
其中是真命题的个数有 ( )
A.1个 B.2个 C.3个 D.4个
9.关于的一元二次方程的两个实数根分别是,,且以,,6为三边的三角形恰好是等腰三角形,则的值为 ( )
A.24 B.25 C.24或25 D.无法确定
10.如图,在平面直角坐标系中,动点A、B分别在x轴上和函数y=x的图像上,AB=4,CB⊥AB,BC=2,则OC的最大值为 ( )
A.2+2 B.2+4 C.2 D.2+2
二、填空题(共6小题,每小题3分,共18分)
11.将59800000用科学记数法表示为__________.
12.若关于的一元一次不等式组的解集是,则的取值范围是______.
13.化简:_________.
14.甲、乙两班举行电脑汉字输入速度比赛,参赛学生每分钟输入汉字的个数经统计计算后结果如下表:
班级 参加人数 中位数 方差 平均数
甲 55 149 191 135
乙 55 151 110 135
某同学根据上表分析得出如下结论:(l)甲、乙两班学生成绩的平均水平相同;(2)乙班优秀(每分钟输入汉字超过150个为优秀)的人数多于甲班优秀的人数;(3)甲班的成绩波动比乙班的成绩波动小、上述结论中正确的是______.(填序号)
15.如图,已知AD是∠BAC的平分线,以线段AB为直径作圆,交∠BAC和角平分线于C,D两点过D向AC作垂线DE垂足为点E,若,则直径________.
第15题图 第16题图
16.如图,双曲线(为常数,)与矩形的边相交于点,与边相交于点,将沿翻折,点恰好落在轴上的点处.则点的坐标为________.
三、解答题:本大题共有7小题,共72分.请将必要的文字说明、计算过程或推理过程写在答题卡的对应位置.
17.(本小题满分6分)计算:.
18.(本小题满分10分)A,B两家酒店规模相当,去年下半年的月盈利折线统计图如图所示.
(1)要评价这两家酒店7~12月的月盈利的平均水平,你选择什么统计量?求出这个统计量;
(2)已知A,B两家酒店7~12月的月盈利的方差分别为1.073(平方万元),0.54(平方万元).根据所给的方差和你在(1)中所求的统计量,结合折线统计图,你认为去年下半年哪家酒店经营状况较好?请简述理由.
(本小题满分10分)如图,我国某海域有,两个港口,相距80海里,港口在港口的东北方向,
点处有一艘货船,该货船在港口的北偏西30°方向,在港口的北偏西75°方向,求货船与港口之间的距离.(结果保留根号)
20.(本小题满分12分)某经销商3月份用18000元购进一批T恤衫售完后,4月份用39000元购进单批相同的T恤衫,数量是3月份的2倍,但每件进价涨了10元.
(1)4月份进了这批T恤衫多少件?
(2)4月份,经销商将这批T恤衫平均分给甲、乙两家分店销售,每件标价180元.甲店按标价卖出a件以后,剩余的按标价八折全部售出;乙店同样按标价卖出a件,然后将b件按标价九折售出,再将剩余的按标价七折全部售出,结果利润与甲店相同.
①用含a的代数式表示b;
②已知乙店按标价售出的数量不超过九折售出的数量,请你求出乙店利润的最大值.
(本小题满分10分)如图,C,D为⊙O上两点,且在直径AB两侧,连结CD交AB于点E,G是上
一点,∠ADC=∠G. (1)求证:∠1=∠2;(2)点C关于DG的对称点为F,连结CF,当点F落在直径AB上时,CF=10,tan∠1=,求⊙O的半径.
22(本小题满分12分)
问题探究:小红遇到这样一个问题:如图1,中,,,AD是中线,求AD的取值范围.她的做法是:延长AD到E,使,连接BE,证明,经过推理和计算使问题得到解决.请回答:
(1)小红证明的判定定理是:________________________;
(2)AD的取值范围是________________________;
方法运用:
(3)如图2,AD是的中线,在AD上取一点F,连结BF并延长交AC于点E,使,求证:.
(4)如图3,在矩形ABCD中,,在BD上取一点F,以BF为斜边作,且,点G是DF的中点,连接EG,CG,求证:.
(本小题满分12分)如图,在平面直角坐标系中,直线分别交x轴、y轴于A,B两点,经
过A,B两点的抛物线与x轴的正半轴相交于点.
(1)求抛物线的解析式;
(2)若P为线段AB上一点,,求AP的长;
(3)在(2)的条件下,设M是y轴上一点,试问:抛物线上是否存在点N,使得以A,P,M,N为顶点的四边形为平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.
参考答案
1.B 【解析】原式.故选:B.
2.D 【解析】由数轴上a与1的位置可知:|a|>1,故选项A错误,不符合题意;
因为a<0,b>0,所以ab<0,故选项B错误,不符合题意;
因为a<0,b>0,所以a-b<0,故选项C错误,不符合题意;
因为a<0,所以1 a>1,故选项D正确,符合题意.
故选:D.
3.D 【解析】将这组数据按从小到大的顺序排列如下:7,8,9,10,12,12,14,16.共8个数据,所以第4个和第5个数的平均数是这组数据的中位数,所以中位数为.
∵12出现了2次是出现次数最多的数,
∴众数是12.
故选D.
4.B 【解析】如图,连接AC,BD,交于点O,
由图可知,,
∵四边形ABCD是正方形,
,
,
,
∴长方体的长和宽都是,高为4,
∴长方体的体积为,
故选:B.
5.A 【解析】函数的自变量的取值范围是:,故选A.
6.C 【解析】由作图可知,CD⊥AB,CE平分∠ACD,
∴∠ACE=∠DCE,
∵∠ACB=∠CDB=90°,
∴∠A+∠B=90°,∠B+∠DCB=90°,
∴∠A=∠DCB,
∵∠BEC=∠A+∠ACE,∠BCE=∠ECD+∠DCB,
∴∠BEC=∠BCE,
∴BC=BE,
故选:C.
7.B 【解析】连接,过作交于,作与,
点为弧的中点,
,
,
,
,
,
,
,
,
,
,
,,
四边形是菱形,
,
,
,
,
.
故选:B.
8.A 【解析】方程,,无实数根,错误;
不等式的解集为,最大整数解是1,错误;
顺次连接对角线相等的四边形各边中点得到的四边形是矩形,说法错误,应为菱形;
直角三角形的两条直角边长分别为6和8,则它的外接圆的半径为,正确;
故选:A.
9.C 【解析】①当6为底边时,则,
∴,
∴,
∴方程为,
解得:,
∵,
∴5,5,6能构成等腰三角形;
②当6为腰时,则设,
∴,
∴,
∴方程为,
∴,,
∵,
∴4,6,6能构成等腰三角形;
综上所述:或25.
故选:C.
10.A 【解析】作以B为圆心,以2为半径的圆,
当OC∥AB时最大,此时OC与圆B相切,
过B作BE⊥x轴于E,过A作AD⊥OC于D,
∵BC⊥AB,OC⊥BC,
∴四边形ABCD为矩形,
∴AD=BC=2,CD=AB=4,
点B在y=x上,点A在x轴上,
设A(n,0),B(m,m),
∵∠OAD+∠BAE=90°,∠BAE+∠ABE=90°,
∴∠OAD=∠ABE,
又∠ODA=∠AEB=90°,
∴△AOD∽△BAE,
∴即,
∴
在RtABE中,
AE=m-n,
由勾股定理得:,
,
,
,
,
,
,
,
,
∵2m4,
∴4m216,
,
在Rt△OAD中,
OD=,
,
,
,
,
,
,
∴OD,
OC=OD+DC=,
故选择:A.
11. 【解析】 .
故答案为:.
12. 【解析】解不等式3x-1>x+3,得:x>2,
∵不等式组的解集为,
∴a>2,
故答案为:a>2.
13. 【解析】
.
故答案为:.
14.(1),(2) 【解析】从表中可知,平均字数都是135,(1)正确;
甲班的中位数是149,乙班的中位数是151,比甲的多,而平均数都要为135,说明乙的优秀人数多于甲班的,(2)正确;
甲班的方差大于乙班的,则说明乙班的波动小,所以(3)错误.
(1)(2)正确.
故答案为(1)(2).
15.10 【解析】连接,,,过点作于点,
,,
,
,
是的平分线,,,
,,
,
,
在中,设,则,
,解得:,
.
故答案为:10.
16., 【解析】作轴于,
设,则,
,,
,
,
,,
,
,
,
,
,
,
,.
故答案为,.
17.
【分析】本题主要考查了整式的混合运算、积的乘方、单项式乘单项式等知识点,灵活运用相关运算法则成为解题的关键.根据整式的混合运算法则计算即可.
【解析】
解:
.(6分)
18.【解析】(1)选择两家酒店月营业额的平均数:
,.(5分)
(2)A酒店营业额的平均数比B酒店的营业额的平均数大,且B酒店的营业额的方差小于A酒店,说明B酒店的营业额比较稳定,而从图像上看A酒店的营业额持续稳定增长,潜力大,说明A酒店经营状况好.(10分)
19.22.【解析】过点作于点
根据题意,得,
∵,
∴,
∴,(3分)
在中,
∵,,
∴,
∵,
∴,(6分)
在中
∵,
∴
答:货船与港口之间的距离是海里.(10分)
20.【解析】(1)设3月份购进T恤x件,
由题意得:,解得x=150,
经检验x=150是分式方程的解,符合题意,
∵4月份是3月份数量的2倍,∴4月份购进T恤300件;(4分)
(2)①由题意得,甲店总收入为,
乙店总收入为,
∵甲乙两店利润相等,成本相等,∴总收入也相等,
∴=,
化简可得,∴用含a的代数式表示b为:;(7分)
②乙店利润函数式为,
结合①可得,
∵,,∴,∴=3900,即最大利润为3900元. (10分)
21.【解析】(1)∵∠ADC=∠G,∴,
∵AB为⊙O的直径,∴,
∴,∴,∴∠1=∠2;(3分)
(2)如图,连接OD、FD,
∵,,∴点C、D关于直径AB对称,
∴AB垂直平分CD,∴FC=FD,CE=DE=CD,∠DEB=90°,(6分)
∵点C关于DG的对称点为F,∴DG垂直平分FC,∴FD=CD,
又∵CF=10,∴FC=FD=CD=10,∴DE=CD=5,
∵在Rt△DEB中,tan∠1=,∴,∴,∴BE=2,(8分)
设OB=OD=x,则OE=x–2,
∵在Rt△DOE中,,
∴,解得:,
∴⊙O的半径为.(10分)
22.【解析】(1)如图,AD是中线,
在与中,,
故答案为:.(2分)
(2)
故答案为:.(4分)
(3)证明:延长至点,使,
∵是的中线,∴,
在和中,,
∴,∴,(6分)
又∵,∴,∴,
又∵,∴,∴,
又∵,∴.(8分)
(4)证明:延长至点使,连接、、,
∵G为的中点,∴,
在和中,,
∴,∴,(9分)
在中,∵,∴,
又矩形中,,
∴,∴,∴,(10分)
又,∴,∴,
又为的外角,∴,
即,
∵,
∴,
∴,即,(11分)
在和中,,∴,
又,∴,∴,
∵,
∴,∴是直角三角形,
∵G为的中点,∴,即.(12分)
23.【解析】(1)令,则,∴点B的坐标为(0,3),
抛物线经过点B (0,3),C (1,0),
∴,解得,
∴抛物线的解析式为:;(4分)
(2)令,则,
解得:,
∴点A的坐标为(,0),
∴OA=3,OB=3,OC=1,
,
∵,且,∴△PAO△CAB,
∴,即,∴;(8分)
(3)存在,(9分)
①当AP为平行四边形的边时.
过点P作PD⊥x轴于点D,
∵OA=3,OB=3,∠AOB=,∴∠BAO=∠ABO=,∴△PAD为等腰直角三角形,
∵,∴PD=AD=2,∴点P的坐标为(,2),
当N在AB的上方时,过点N作NE⊥y轴于点E,如图,
∵四边形APMN为平行四边形,∴NM∥AP,NM=AP=,
∴∠NME=∠ABO=,∴△NME为等腰直角三角形,
∴Rt△NMERt△APD,∴NE=AD=2,
当时,,∴点N的坐标为(,3). (10分)
当N在AB的下方时,过点N作NF⊥y轴于点F,如图,
同理可得:Rt△NMFRt△APD,∴NF=AD=2,
当时,,∴点N的坐标为(,).(11分)
②当AP为平行四边形的对角线时,点N的坐标为(–4,).
综上,点N的坐标为(,3) 或(,) 或(–4,).(12分)
同课章节目录
