人教版八年级下册17.1 勾股定理 同步练习(含答案)
文档属性
| 名称 | 人教版八年级下册17.1 勾股定理 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-10 18:26:27 | ||
图片预览


文档简介
17.1 勾股定理 同步练习
一、单选题(共12小题)
1. 在 中,若 ,则 是
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 形状不确定
2. 三角形的三边长 ,, 满足 ,则此三角形是
A. 直角三角形 B. 锐角三角形 C. 钝角三角形 D. 等腰三角形
3. 如图,在 中,, 于点 ,则图中直角三角形有 .
A. 个 B. 个 C. 个 D. 个
4. 若直角三角形的三边长分别为 ,,,则 的可能值有
A. 个 B. 个 C. 个 D. 个
5. 如图,数轴上,下列各数是无理数且表示的点在线段 上的是
A. B. C. D.
6. 如图是一个台阶示意图,每一层台阶的高都是 ,长都是 ,宽都是 ,一只蚂蚁沿台阶从 点出发到点 ,其爬行的最短路线的长度是
A. B. C. D.
7. 如图所示,正方体的棱长为 ,一只蜘蛛从正方体的一个顶点 爬行到另一个顶点 ,则蜘蛛爬行的最短距离的平方是
A. B. C. D.
8. 如图,圆柱形容器的高为 ,底面周长为 ,在杯内壁离杯底 的点 处有几滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿 与蜂蜜相对的点 处,则蚂蚁从外壁 处到达内壁 处的最短距离为
A. B. C. D.
9. 在 中,若 ,则此三角形是
A. 钝角三角形 B. 直角三角形 C. 锐角三角形 D. 无法确定
10. 如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆 处,发现此时绳子末端距离地面 ,则旗杆的高度(滑轮上方的部分忽略不计)为
A. B. C. D.
11. 如图,在正方形 中,, 是 边上的一点,.将 沿 对折至 ,连接 ,则 的长是
A. B. C. D.
12. 如图,在 中,,,, 为线段 上两动点,且 ,过点 , 分别作 , 的垂线相交于点 ,垂足分别为 ,.现有以下结论:① ;② 当点 与点 重合时,;③ ;④ ,其中正确结论为
A. ① ② ③ B. ① ③ ④ C. ① ② ④ D. ① ② ③ ④
二、填空题(共6小题)
13. 在 中,锐角 ,则另一个锐角
14. 在直角三角形 中,,则它的三条边 ,, 中,最长的边是 .
15. 已知甲、乙两人在同一地点出发,甲往东走了 ,乙往南走了 ,这时甲、乙两人相距 .
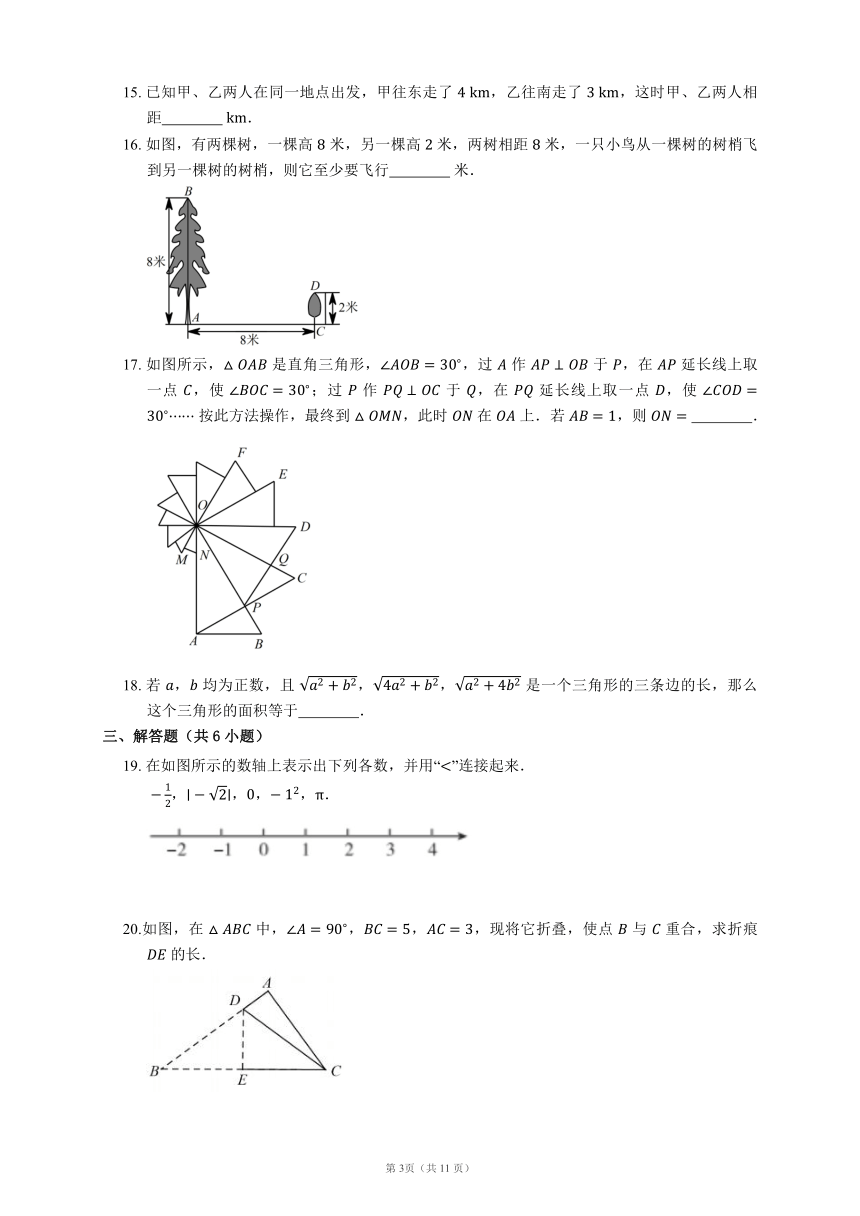
16. 如图,有两棵树,一棵高 米,另一棵高 米,两树相距 米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,则它至少要飞行 米.
17. 如图所示, 是直角三角形,,过 作 于 ,在 延长线上取一点 ,使 ;过 作 于 ,在 延长线上取一点 ,使 按此方法操作,最终到 ,此时 在 上.若 ,则 .
18. 若 , 均为正数,且 ,, 是一个三角形的三条边的长,那么这个三角形的面积等于 .
三、解答题(共6小题)
19. 在如图所示的数轴上表示出下列各数,并用“”连接起来.
,,,,.
20.如图,在 中,,,,现将它折叠,使点 与 重合,求折痕 的长.
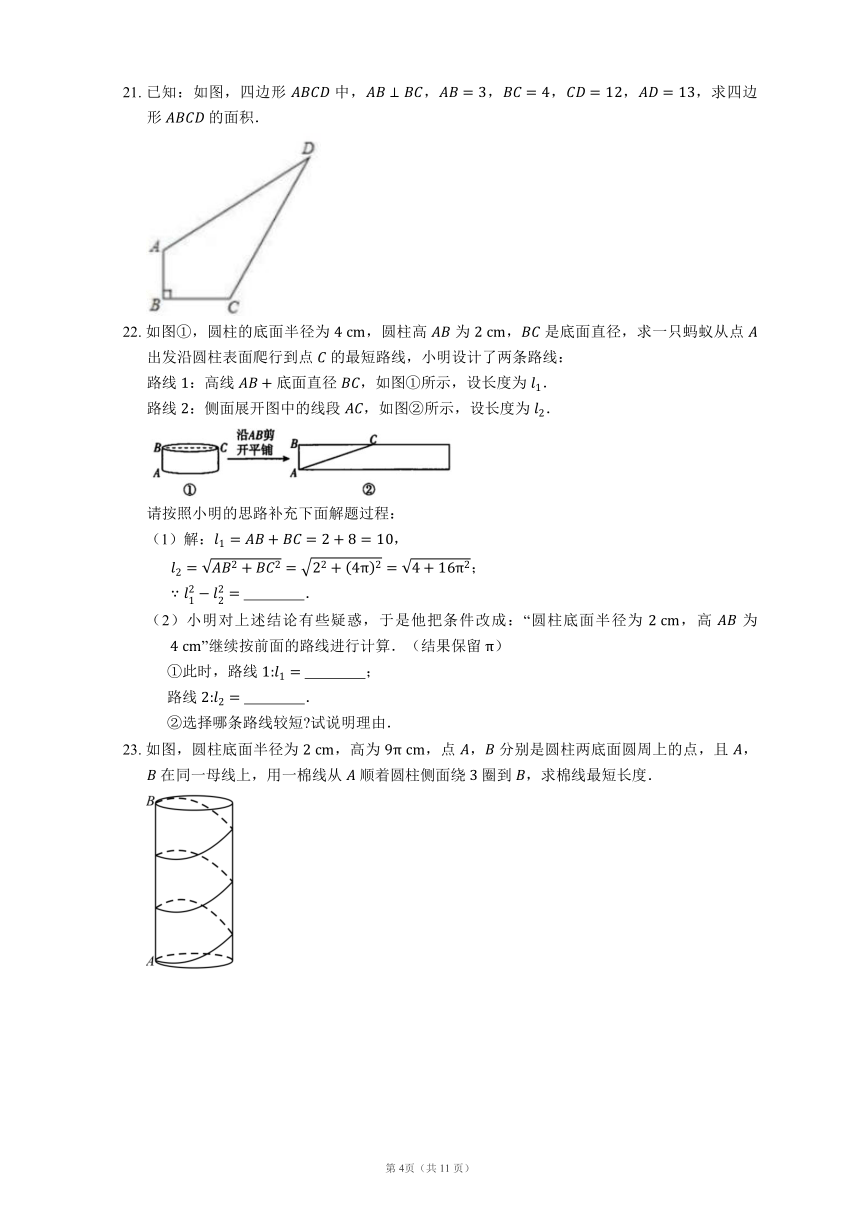
21. 已知:如图,四边形 中,,,,,,求四边形 的面积.
22. 如图①,圆柱的底面半径为 ,圆柱高 为 , 是底面直径,求一只蚂蚁从点 出发沿圆柱表面爬行到点 的最短路线,小明设计了两条路线:
路线 :高线 底面直径 ,如图①所示,设长度为 .
路线 :侧面展开图中的线段 ,如图②所示,设长度为 .
请按照小明的思路补充下面解题过程:
(1)解:,
;
.
(2)小明对上述结论有些疑惑,于是他把条件改成:“圆柱底面半径为 ,高 为 ”继续按前面的路线进行计算.(结果保留 )
①此时,路线 ;
路线 .
②选择哪条路线较短 试说明理由.
23. 如图,圆柱底面半径为 ,高为 ,点 , 分别是圆柱两底面圆周上的点,且 , 在同一母线上,用一棉线从 顺着圆柱侧面绕 圈到 ,求棉线最短长度.
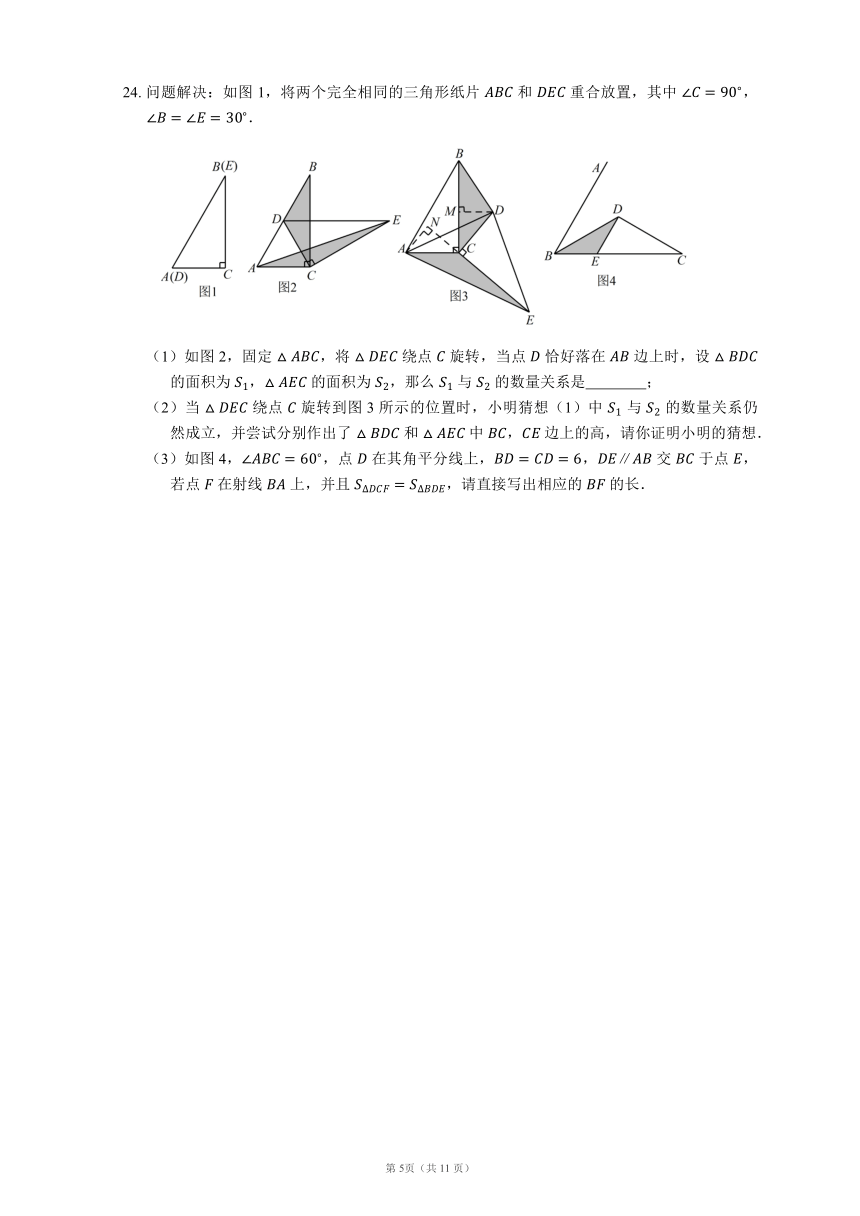
24. 问题解决:如图 1,将两个完全相同的三角形纸片 和 重合放置,其中 ,.
(1)如图 2,固定 ,将 绕点 旋转,当点 恰好落在 边上时,设 的面积为 , 的面积为 ,那么 与 的数量关系是 ;
(2)当 绕点 旋转到图 3 所示的位置时,小明猜想(1)中 与 的数量关系仍然成立,并尝试分别作出了 和 中 , 边上的高,请你证明小明的猜想.
(3)如图 4,,点 在其角平分线上,, 交 于点 ,若点 在射线 上,并且 ,请直接写出相应的 的长.
答案
一 单选题
1. B
2. A
【解析】 ,
,
.
3. D
4. B
5. B
6. C
【解析】把图形展直,根据勾股定理,可得蚂蚁爬行的最短路线的长度是 .
7. D
【解析】将正方体的前面、上面展开放在同一平面上,连接 ,如图所示,
爬行的最短路径为线段 .
由勾股定理得,,
故选D.
8. D
9. B
10. D
【解析】由题意得 ,, .
由勾股定理,得 即 .
解得 .
11. D
【解析】连接 交 于点 ,作 于点 .如图:
,,
,.
四边形 是正方形,
.
根据折叠性质,,,.
,
.
.
,
.
.
.
.
.
.
12. C
【解析】根据勾股定理,.
当点 与点 重合时,点 与点 重合, 为 中点.
此时 .
如图,
,,
.
将 顺时针旋转 至 ,则 ,,,.
,
,
.
().
.
,
,
,即 .故③错;
,,
,
,
.
根据四边形 是矩形,
所以 ,,
即 ,,
,,
.
二 填空题
13. 度
14.
15.
16.
【解析】过点 作 于 ,连接 .
在 中, 米, 米.
根据勾股定理得 米.
17.
【解析】,,,
,.
为等边三角形的高,且等边三角形的边长为 ,
,
以此类推,当 与 重合时,一共旋转了 次,
的长为 .
18.
【解析】如图所示,连接 .
矩形 中, 、 分别是边 、 的中点,且 ,,
则 ,,.
故 .
三 解答题
19. 如图所示.
.
20. 由折叠的性质可得:,,,
,
,,,
,
;
在 中,由勾股定理得:,
解得:,
在 中,由勾股定理得:.
答:折痕 的长为 .
21. 连接 ,
在 中,
,,
,
,
在 中,
,,,
,
是直角三角形,
.
四边形 的面积 .
22. (1)
【解析】,
,
,
,即 ,所以选择路线 较短.
(2) ① ;
② .
,即 .
所以选择路线 较短.
23. 圆柱体的展开图如图所示,
用一棉线从 顺着圆柱侧面绕 圈到 的运动最短路线是:,即在圆柱体的展开图长方形中,将长方形平均分成 个小长方形, 沿着 个小长方形的对角线运动到 的路线最短.
圆柱底面半径为 ,
长方形的宽即是圆柱体的底面圆的周长为 .
又圆柱高为 ,
小长方体的一条边长是 .
根据勾股定理求得 .
.
故棉线的最短长度为 .
24. (1) 相等
【解析】由 ,,
可得 ,
根据旋转的性质可知 .
由 ,可得 为等边三角形,,
在等边三角形 中, 、 边上的高相等,
所以 .
(2) , 分别是 和 中 , 边上的高,
.
,
,
,
,
,
.
,
().
.
,,且 ,
.
(3) 或 .
【解析】
如图,易得 ,.
第1页(共11 页)
一、单选题(共12小题)
1. 在 中,若 ,则 是
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 形状不确定
2. 三角形的三边长 ,, 满足 ,则此三角形是
A. 直角三角形 B. 锐角三角形 C. 钝角三角形 D. 等腰三角形
3. 如图,在 中,, 于点 ,则图中直角三角形有 .
A. 个 B. 个 C. 个 D. 个
4. 若直角三角形的三边长分别为 ,,,则 的可能值有
A. 个 B. 个 C. 个 D. 个
5. 如图,数轴上,下列各数是无理数且表示的点在线段 上的是
A. B. C. D.
6. 如图是一个台阶示意图,每一层台阶的高都是 ,长都是 ,宽都是 ,一只蚂蚁沿台阶从 点出发到点 ,其爬行的最短路线的长度是
A. B. C. D.
7. 如图所示,正方体的棱长为 ,一只蜘蛛从正方体的一个顶点 爬行到另一个顶点 ,则蜘蛛爬行的最短距离的平方是
A. B. C. D.
8. 如图,圆柱形容器的高为 ,底面周长为 ,在杯内壁离杯底 的点 处有几滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿 与蜂蜜相对的点 处,则蚂蚁从外壁 处到达内壁 处的最短距离为
A. B. C. D.
9. 在 中,若 ,则此三角形是
A. 钝角三角形 B. 直角三角形 C. 锐角三角形 D. 无法确定
10. 如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆 处,发现此时绳子末端距离地面 ,则旗杆的高度(滑轮上方的部分忽略不计)为
A. B. C. D.
11. 如图,在正方形 中,, 是 边上的一点,.将 沿 对折至 ,连接 ,则 的长是
A. B. C. D.
12. 如图,在 中,,,, 为线段 上两动点,且 ,过点 , 分别作 , 的垂线相交于点 ,垂足分别为 ,.现有以下结论:① ;② 当点 与点 重合时,;③ ;④ ,其中正确结论为
A. ① ② ③ B. ① ③ ④ C. ① ② ④ D. ① ② ③ ④
二、填空题(共6小题)
13. 在 中,锐角 ,则另一个锐角
14. 在直角三角形 中,,则它的三条边 ,, 中,最长的边是 .
15. 已知甲、乙两人在同一地点出发,甲往东走了 ,乙往南走了 ,这时甲、乙两人相距 .
16. 如图,有两棵树,一棵高 米,另一棵高 米,两树相距 米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,则它至少要飞行 米.
17. 如图所示, 是直角三角形,,过 作 于 ,在 延长线上取一点 ,使 ;过 作 于 ,在 延长线上取一点 ,使 按此方法操作,最终到 ,此时 在 上.若 ,则 .
18. 若 , 均为正数,且 ,, 是一个三角形的三条边的长,那么这个三角形的面积等于 .
三、解答题(共6小题)
19. 在如图所示的数轴上表示出下列各数,并用“”连接起来.
,,,,.
20.如图,在 中,,,,现将它折叠,使点 与 重合,求折痕 的长.
21. 已知:如图,四边形 中,,,,,,求四边形 的面积.
22. 如图①,圆柱的底面半径为 ,圆柱高 为 , 是底面直径,求一只蚂蚁从点 出发沿圆柱表面爬行到点 的最短路线,小明设计了两条路线:
路线 :高线 底面直径 ,如图①所示,设长度为 .
路线 :侧面展开图中的线段 ,如图②所示,设长度为 .
请按照小明的思路补充下面解题过程:
(1)解:,
;
.
(2)小明对上述结论有些疑惑,于是他把条件改成:“圆柱底面半径为 ,高 为 ”继续按前面的路线进行计算.(结果保留 )
①此时,路线 ;
路线 .
②选择哪条路线较短 试说明理由.
23. 如图,圆柱底面半径为 ,高为 ,点 , 分别是圆柱两底面圆周上的点,且 , 在同一母线上,用一棉线从 顺着圆柱侧面绕 圈到 ,求棉线最短长度.
24. 问题解决:如图 1,将两个完全相同的三角形纸片 和 重合放置,其中 ,.
(1)如图 2,固定 ,将 绕点 旋转,当点 恰好落在 边上时,设 的面积为 , 的面积为 ,那么 与 的数量关系是 ;
(2)当 绕点 旋转到图 3 所示的位置时,小明猜想(1)中 与 的数量关系仍然成立,并尝试分别作出了 和 中 , 边上的高,请你证明小明的猜想.
(3)如图 4,,点 在其角平分线上,, 交 于点 ,若点 在射线 上,并且 ,请直接写出相应的 的长.
答案
一 单选题
1. B
2. A
【解析】 ,
,
.
3. D
4. B
5. B
6. C
【解析】把图形展直,根据勾股定理,可得蚂蚁爬行的最短路线的长度是 .
7. D
【解析】将正方体的前面、上面展开放在同一平面上,连接 ,如图所示,
爬行的最短路径为线段 .
由勾股定理得,,
故选D.
8. D
9. B
10. D
【解析】由题意得 ,, .
由勾股定理,得 即 .
解得 .
11. D
【解析】连接 交 于点 ,作 于点 .如图:
,,
,.
四边形 是正方形,
.
根据折叠性质,,,.
,
.
.
,
.
.
.
.
.
.
12. C
【解析】根据勾股定理,.
当点 与点 重合时,点 与点 重合, 为 中点.
此时 .
如图,
,,
.
将 顺时针旋转 至 ,则 ,,,.
,
,
.
().
.
,
,
,即 .故③错;
,,
,
,
.
根据四边形 是矩形,
所以 ,,
即 ,,
,,
.
二 填空题
13. 度
14.
15.
16.
【解析】过点 作 于 ,连接 .
在 中, 米, 米.
根据勾股定理得 米.
17.
【解析】,,,
,.
为等边三角形的高,且等边三角形的边长为 ,
,
以此类推,当 与 重合时,一共旋转了 次,
的长为 .
18.
【解析】如图所示,连接 .
矩形 中, 、 分别是边 、 的中点,且 ,,
则 ,,.
故 .
三 解答题
19. 如图所示.
.
20. 由折叠的性质可得:,,,
,
,,,
,
;
在 中,由勾股定理得:,
解得:,
在 中,由勾股定理得:.
答:折痕 的长为 .
21. 连接 ,
在 中,
,,
,
,
在 中,
,,,
,
是直角三角形,
.
四边形 的面积 .
22. (1)
【解析】,
,
,
,即 ,所以选择路线 较短.
(2) ① ;
② .
,即 .
所以选择路线 较短.
23. 圆柱体的展开图如图所示,
用一棉线从 顺着圆柱侧面绕 圈到 的运动最短路线是:,即在圆柱体的展开图长方形中,将长方形平均分成 个小长方形, 沿着 个小长方形的对角线运动到 的路线最短.
圆柱底面半径为 ,
长方形的宽即是圆柱体的底面圆的周长为 .
又圆柱高为 ,
小长方体的一条边长是 .
根据勾股定理求得 .
.
故棉线的最短长度为 .
24. (1) 相等
【解析】由 ,,
可得 ,
根据旋转的性质可知 .
由 ,可得 为等边三角形,,
在等边三角形 中, 、 边上的高相等,
所以 .
(2) , 分别是 和 中 , 边上的高,
.
,
,
,
,
,
.
,
().
.
,,且 ,
.
(3) 或 .
【解析】
如图,易得 ,.
第1页(共11 页)
