浙江省慈溪市三山高级中学华师大版八年级数学上册课件:14.2勾股定理的应用(共11张PPT)
文档属性
| 名称 | 浙江省慈溪市三山高级中学华师大版八年级数学上册课件:14.2勾股定理的应用(共11张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 376.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-04 08:38:36 | ||
图片预览


文档简介
课件11张PPT。 华东版八年级(上)第十四章
勾股定理的应用
荷花问题
平平湖水清可鉴,
面上半尺生红莲;
出泥不染亭亭立,
忽被强风吹一边;
渔人观看忙向前,
花离原位二尺远;
能算诸君请解题,
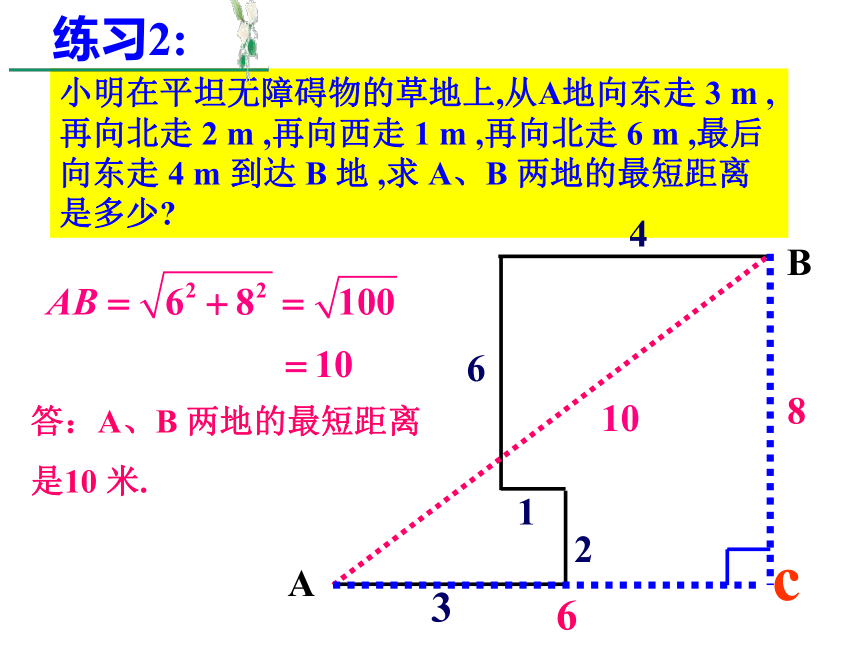
湖水如何知深浅. 0.5xx+0.52答:湖水深3.75尺.练习1:可用勾股定理建立方程.小明在平坦无障碍物的草地上,从A地向东走 3 m ,再向北走 2 m ,再向西走 1 m ,再向北走 6 m ,最后向东走 4 m 到达 B 地 ,求 A、B 两地的最短距离是多少?c68答:A、B 两地的最短距离
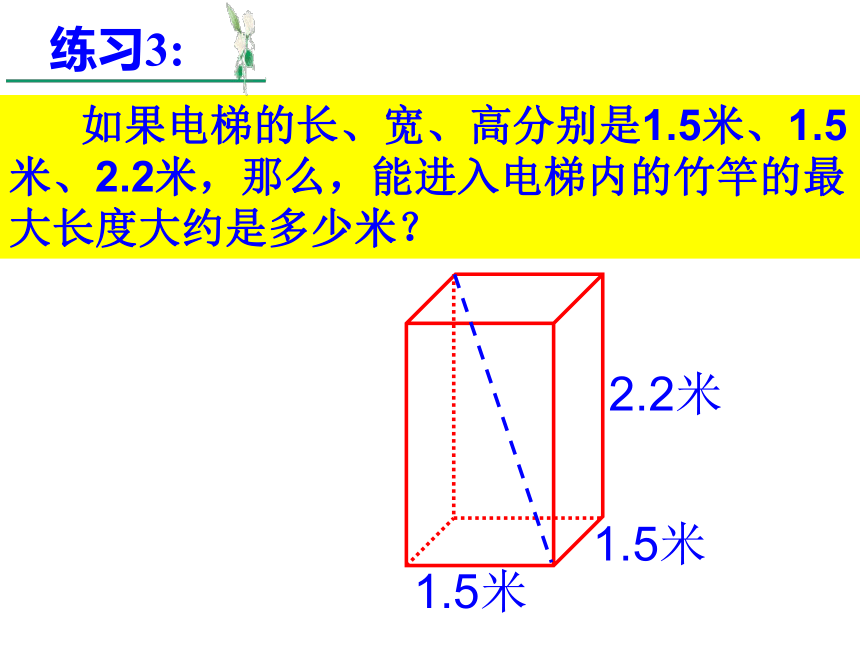
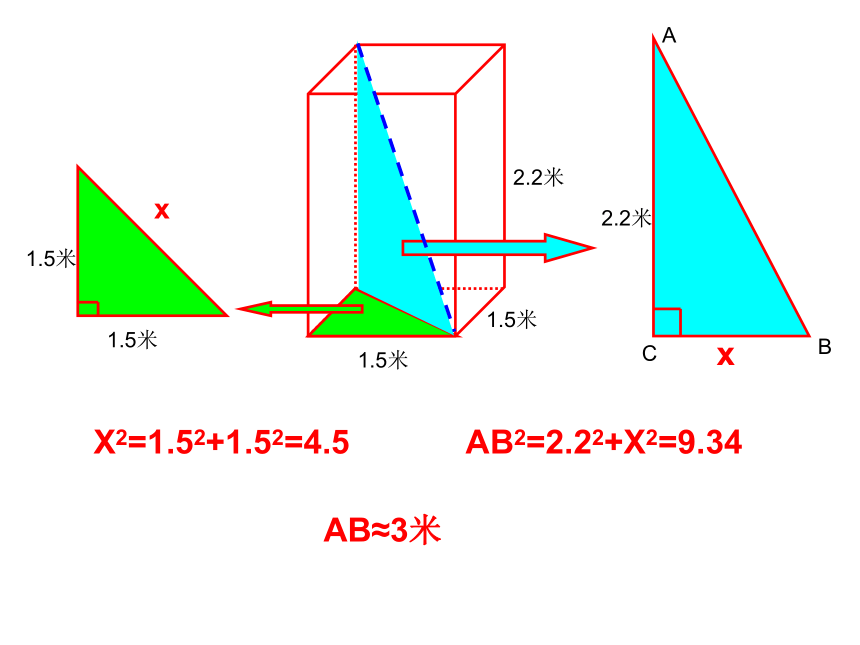
是10 米.练习2: 如果电梯的长、宽、高分别是1.5米、1.5米、2.2米,那么,能进入电梯内的竹竿的最大长度大约是多少米?练习3:1.5米1.5米2.2米xX2=1.52+1.52=4.5AB2=2.22+X2=9.34AB≈3米有一圆柱,底面圆的周长为24cm,高为6cm,一只蚂蚁从底面的A处爬行到对角B处吃食物,它爬行的最短路线长为多少?AB蚂蚁从距底面1cm的A处爬行到对角B处吃食物,它爬行的最短路线长为多少?AB探究1:分析:由于蚂蚁是沿着圆柱的表面爬行的,故需把圆柱展开成平面图形.根据两点之间线段最短,可以发现A、B分别在圆柱侧面展开图的宽6cm处和长24cm中点处,即AB长为最短路线.(如图)12612513展开问题变式1:
有一木质圆柱形笔筒的高为h,底面半径为r,现要围绕笔筒的表面由A至C,(A,C在圆柱的同一轴截面上)镶入一条银色金属线作为装饰,这条金属线的最短长度是多少?CBADC101010BCAC 变式2:如果圆柱换成如图的棱长为10cm的正方体盒子,蚂蚁沿着表面由A至B需要爬行的最短路程又是多少呢? 变式3:如果盒子换成如图长为3cm,宽为2cm,高为1cm的长方体,蚂蚁沿着表面需要爬行的最短路程又是多少呢?321小结
①本节课学到了什么数学知识?
②你了解勾股定理的发现方法了吗?
③你还有什么困惑?谢谢!再见!
勾股定理的应用
荷花问题
平平湖水清可鉴,
面上半尺生红莲;
出泥不染亭亭立,
忽被强风吹一边;
渔人观看忙向前,
花离原位二尺远;
能算诸君请解题,
湖水如何知深浅. 0.5xx+0.52答:湖水深3.75尺.练习1:可用勾股定理建立方程.小明在平坦无障碍物的草地上,从A地向东走 3 m ,再向北走 2 m ,再向西走 1 m ,再向北走 6 m ,最后向东走 4 m 到达 B 地 ,求 A、B 两地的最短距离是多少?c68答:A、B 两地的最短距离
是10 米.练习2: 如果电梯的长、宽、高分别是1.5米、1.5米、2.2米,那么,能进入电梯内的竹竿的最大长度大约是多少米?练习3:1.5米1.5米2.2米xX2=1.52+1.52=4.5AB2=2.22+X2=9.34AB≈3米有一圆柱,底面圆的周长为24cm,高为6cm,一只蚂蚁从底面的A处爬行到对角B处吃食物,它爬行的最短路线长为多少?AB蚂蚁从距底面1cm的A处爬行到对角B处吃食物,它爬行的最短路线长为多少?AB探究1:分析:由于蚂蚁是沿着圆柱的表面爬行的,故需把圆柱展开成平面图形.根据两点之间线段最短,可以发现A、B分别在圆柱侧面展开图的宽6cm处和长24cm中点处,即AB长为最短路线.(如图)12612513展开问题变式1:
有一木质圆柱形笔筒的高为h,底面半径为r,现要围绕笔筒的表面由A至C,(A,C在圆柱的同一轴截面上)镶入一条银色金属线作为装饰,这条金属线的最短长度是多少?CBADC101010BCAC 变式2:如果圆柱换成如图的棱长为10cm的正方体盒子,蚂蚁沿着表面由A至B需要爬行的最短路程又是多少呢? 变式3:如果盒子换成如图长为3cm,宽为2cm,高为1cm的长方体,蚂蚁沿着表面需要爬行的最短路程又是多少呢?321小结
①本节课学到了什么数学知识?
②你了解勾股定理的发现方法了吗?
③你还有什么困惑?谢谢!再见!
