初中数学人教版八年级下册 17.2 勾股定理的逆定理 同步练习(含答案)
文档属性
| 名称 | 初中数学人教版八年级下册 17.2 勾股定理的逆定理 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 381.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-10 00:00:00 | ||
图片预览



文档简介
17.2 勾股定理的逆定理 同步练习
一、单选题(共12小题)
1. 下列四组数,是勾股数的是
A. ,, B. ,, C. ,, D. ,,
2. 由线段 ,, 组成的三角形中,不能组成直角三角形的是
A. ,, B. ,,
C. ,, D. ,,
3. 在下列命题中,逆命题是假命题的是
A. 两直线平行,同旁内角互补
B. 如果两个三角形全等,那么这两个三角形的对应边相等
C. 如果两个三角形全等,那么这两个三角形的对应角相等
D. 线段垂直平分线上的任意一点到这条线段两个端点的距离相等
4. 下列说法正确的是
A. 一个三角形的三边长分别为 ,,,且 ,则这个三角形是直角三角形
B. 三边长度分别为 ,, 的三角形是直角三角形,且 ,, 是一组勾股数
C. 三边长度分别是 ,, 的三角形是直角三角形
D. 在一个直角三角形中,有两边的长度分别是 和 ,则第三边的长度一定是
5. 一个三角形的三边的比为 ,则这个三角形的形状
A. 直角三角形 B. 锐角三角形 C. 钝角三角性 D. 不确定
6. 三角形的三边 ,, 满足 ,则此三角形是
A. 等腰三角形B. 等腰直角三角形C. 直角三角形D. 无法判断
7. 某住宅小区有一块草坪,如图所示,已知 ,,, ,且 ,则这块草坪的面积是
A. B. C. D.
8. 如图是一个 的正方形网格,每个小正方形的顶点都是格点, 的顶点都是图中的格点,其中点 、点 的位置如图所示,则点 可能的位置共有
A. 个 B. 个 C. 个 D. 个
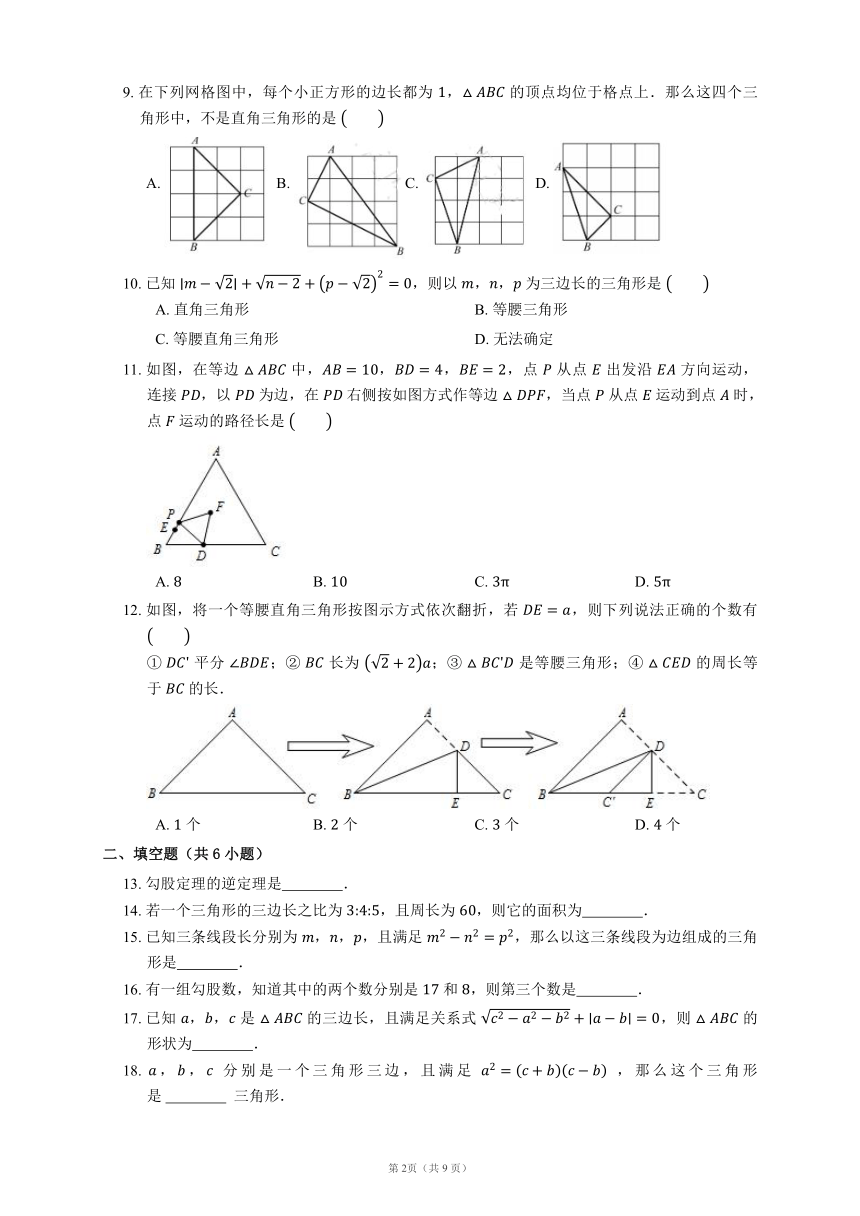
9. 在下列网格图中,每个小正方形的边长都为 , 的顶点均位于格点上.那么这四个三角形中,不是直角三角形的是
A. B. C. D.
10. 已知 ,则以 ,, 为三边长的三角形是
A. 直角三角形 B. 等腰三角形
C. 等腰直角三角形 D. 无法确定
11. 如图,在等边 中,,,,点 从点 出发沿 方向运动,连接 ,以 为边,在 右侧按如图方式作等边 ,当点 从点 运动到点 时,点 运动的路径长是
A. B. C. D.
12. 如图,将一个等腰直角三角形按图示方式依次翻折,若 ,则下列说法正确的个数有
① 平分 ;② 长为 ;③ 是等腰三角形;④ 的周长等于 的长.
A. 个 B. 个 C. 个 D. 个
二、填空题(共6小题)
13. 勾股定理的逆定理是 .
14. 若一个三角形的三边长之比为 ,且周长为 ,则它的面积为 .
15. 已知三条线段长分别为 ,,,且满足 ,那么以这三条线段为边组成的三角形是 .
16. 有一组勾股数,知道其中的两个数分别是 和 ,则第三个数是 .
17. 已知 ,, 是 的三边长,且满足关系式 ,则 的形状为 .
18. ,, 分别是一个三角形三边,且满足 ,那么这个三角形是 三角形.
三、解答题(共6小题)
19.写出下列命题的逆命题:
(1)等腰三角形的底角相等;
(2)等边三角形是轴对称图形;
(3)正方形的四条边相等;
(4)如果两个角不相等,那么这两个角不是对顶角;
(5)全等三角形的面积相等.
20. 若 ,, 是 的三条边,且 ,判断 的形状.
21. 一个零件的形状如图所示,工人师傅按规定做得 ,,,,,假如这是一块钢板,请你帮工人师傅计算一下这块钢板的面积.
22. 王老师在一次“探究性学习”课中,设计了如下数表:
(1)请你分别观察 ,, 与 之间的关系,并用含自然数 的代数式表示:
, , .
(2)猜想:以 ,, 为边的三角形是否为直角三角形 并证明你的猜想
(3)请你观察下列四组勾股数:;;;,分析其中的规律,直接写出第五组勾股数 .
23. 如图, 为 的 边上的一点,,,,.
(1)求 的长;
(2)求 的面积.
24. 请回答:
(1)【问题解决】
一节数学课上,老师提出了这样一个问题:如图①,点 是正方形 内一点,,,.你能求出 的度数吗
小明通过观察、分析、思考,形成了如下思路:
思路一:将 绕点 逆时针旋转 ,得到 ,连接 ,求出 的度数;
思路二:将 绕点 顺时针旋转 ,得到 .连接 ,求出 的度数.
请参考小明的思路,任选一种写出完整的解答过程.
(2)【类比探究】
如图②,若点 是正方形 外一点,,,,求 的度数.
答案
一 单选题
1. B
2. D
3. C
4. A
【解析】A项说法正确,符合题意;
B.勾股数必须都是正整数,故B项说法错误,不符合题意;
C.,
三边长度分别是 ,, 的三角形是直角三角形的说法错误,不符合题意;
D.在一个直角三角形中,有两边的长度分别是 和 ,则第三边的长度是 或 ,故说法错误,不符合题意.
故选A.
5. A
6. C
7. B
8. A
【解析】
9. C
【解析】
10. C
11. A
【解析】
如图,连接 ,作 于 ,
为等边三角形,
.
作 于 ,
易得 ,,,,
,
.
可证 ,
,
点 从点 运动到点 时,点 的运动路径为一条线段,此线段到 的距离为 .
当点 在点 和 时,分别作等边三角形,如图所示,
可证 ,
.
12. C
【解析】 是等腰直角三角形,
,.
第一次翻折时,可知 平分 ,, 是等腰三角形.
第二次翻折时,可知 ,,.
,.
则①是错误的.
,
,.
.
则②是正确的.
,
是等腰三角形.
则③是正确的.
的周长 .
则④是正确的.
二 填空题
13. 如果三角形的三边长 ,,,满足 ,那么这个三角形是直角三角形
14.
15. 直角三角形
16.
17. 等腰直角三角形.
【解析】由题意,得 ,,
,.
是等腰直角三角形.
18. 直角
【解析】提示: .
三 解答题
19. (1) 有两个内角相等的三角形是等腰三角形.
(2) 轴对称图形都是等边三角形.
(3) 四条边相等的图形是正方形.
(4) 如果两个角不是对顶角,那么这两个角不想等.
(5) 面积相等的两个三角形是全等三角形.
20. 原式可变形为 ,
即 ,
,,,
,
为直角三角形.
21. 在 中,,
,
在 中,,
,
22. (1) ;;
【解析】由题意:,,.
故答案为:,,.
(2) 猜想:以 ,, 为边的三角形是直角三角形.
理由:
,,,
,
以 ,, 为边的三角形是直角三角形.
(3)
【解析】观察可知:第五组勾股数为:.
故答案为:.
23. (1) ,,
.
,
.
(2) 在 中,,,,
,
为直角三角形,即 .
,,
.
24. (1) 选思路一:如图①,将 绕点 逆时针旋转 ,得到 ,连接 ,
,
,,,
在 中,,
,
根据勾股定理得,,
,
,
,
,
是直角三角形,且 ,
.
(2) 如图②,将 绕点 逆时针旋转 ,得到 ,连接 ,
,
,,,
在 中,,
,
根据勾股定理得,,
,
,
,
,
是直角三角形,且 ,
.
第1页(共9 页)
一、单选题(共12小题)
1. 下列四组数,是勾股数的是
A. ,, B. ,, C. ,, D. ,,
2. 由线段 ,, 组成的三角形中,不能组成直角三角形的是
A. ,, B. ,,
C. ,, D. ,,
3. 在下列命题中,逆命题是假命题的是
A. 两直线平行,同旁内角互补
B. 如果两个三角形全等,那么这两个三角形的对应边相等
C. 如果两个三角形全等,那么这两个三角形的对应角相等
D. 线段垂直平分线上的任意一点到这条线段两个端点的距离相等
4. 下列说法正确的是
A. 一个三角形的三边长分别为 ,,,且 ,则这个三角形是直角三角形
B. 三边长度分别为 ,, 的三角形是直角三角形,且 ,, 是一组勾股数
C. 三边长度分别是 ,, 的三角形是直角三角形
D. 在一个直角三角形中,有两边的长度分别是 和 ,则第三边的长度一定是
5. 一个三角形的三边的比为 ,则这个三角形的形状
A. 直角三角形 B. 锐角三角形 C. 钝角三角性 D. 不确定
6. 三角形的三边 ,, 满足 ,则此三角形是
A. 等腰三角形B. 等腰直角三角形C. 直角三角形D. 无法判断
7. 某住宅小区有一块草坪,如图所示,已知 ,,, ,且 ,则这块草坪的面积是
A. B. C. D.
8. 如图是一个 的正方形网格,每个小正方形的顶点都是格点, 的顶点都是图中的格点,其中点 、点 的位置如图所示,则点 可能的位置共有
A. 个 B. 个 C. 个 D. 个
9. 在下列网格图中,每个小正方形的边长都为 , 的顶点均位于格点上.那么这四个三角形中,不是直角三角形的是
A. B. C. D.
10. 已知 ,则以 ,, 为三边长的三角形是
A. 直角三角形 B. 等腰三角形
C. 等腰直角三角形 D. 无法确定
11. 如图,在等边 中,,,,点 从点 出发沿 方向运动,连接 ,以 为边,在 右侧按如图方式作等边 ,当点 从点 运动到点 时,点 运动的路径长是
A. B. C. D.
12. 如图,将一个等腰直角三角形按图示方式依次翻折,若 ,则下列说法正确的个数有
① 平分 ;② 长为 ;③ 是等腰三角形;④ 的周长等于 的长.
A. 个 B. 个 C. 个 D. 个
二、填空题(共6小题)
13. 勾股定理的逆定理是 .
14. 若一个三角形的三边长之比为 ,且周长为 ,则它的面积为 .
15. 已知三条线段长分别为 ,,,且满足 ,那么以这三条线段为边组成的三角形是 .
16. 有一组勾股数,知道其中的两个数分别是 和 ,则第三个数是 .
17. 已知 ,, 是 的三边长,且满足关系式 ,则 的形状为 .
18. ,, 分别是一个三角形三边,且满足 ,那么这个三角形是 三角形.
三、解答题(共6小题)
19.写出下列命题的逆命题:
(1)等腰三角形的底角相等;
(2)等边三角形是轴对称图形;
(3)正方形的四条边相等;
(4)如果两个角不相等,那么这两个角不是对顶角;
(5)全等三角形的面积相等.
20. 若 ,, 是 的三条边,且 ,判断 的形状.
21. 一个零件的形状如图所示,工人师傅按规定做得 ,,,,,假如这是一块钢板,请你帮工人师傅计算一下这块钢板的面积.
22. 王老师在一次“探究性学习”课中,设计了如下数表:
(1)请你分别观察 ,, 与 之间的关系,并用含自然数 的代数式表示:
, , .
(2)猜想:以 ,, 为边的三角形是否为直角三角形 并证明你的猜想
(3)请你观察下列四组勾股数:;;;,分析其中的规律,直接写出第五组勾股数 .
23. 如图, 为 的 边上的一点,,,,.
(1)求 的长;
(2)求 的面积.
24. 请回答:
(1)【问题解决】
一节数学课上,老师提出了这样一个问题:如图①,点 是正方形 内一点,,,.你能求出 的度数吗
小明通过观察、分析、思考,形成了如下思路:
思路一:将 绕点 逆时针旋转 ,得到 ,连接 ,求出 的度数;
思路二:将 绕点 顺时针旋转 ,得到 .连接 ,求出 的度数.
请参考小明的思路,任选一种写出完整的解答过程.
(2)【类比探究】
如图②,若点 是正方形 外一点,,,,求 的度数.
答案
一 单选题
1. B
2. D
3. C
4. A
【解析】A项说法正确,符合题意;
B.勾股数必须都是正整数,故B项说法错误,不符合题意;
C.,
三边长度分别是 ,, 的三角形是直角三角形的说法错误,不符合题意;
D.在一个直角三角形中,有两边的长度分别是 和 ,则第三边的长度是 或 ,故说法错误,不符合题意.
故选A.
5. A
6. C
7. B
8. A
【解析】
9. C
【解析】
10. C
11. A
【解析】
如图,连接 ,作 于 ,
为等边三角形,
.
作 于 ,
易得 ,,,,
,
.
可证 ,
,
点 从点 运动到点 时,点 的运动路径为一条线段,此线段到 的距离为 .
当点 在点 和 时,分别作等边三角形,如图所示,
可证 ,
.
12. C
【解析】 是等腰直角三角形,
,.
第一次翻折时,可知 平分 ,, 是等腰三角形.
第二次翻折时,可知 ,,.
,.
则①是错误的.
,
,.
.
则②是正确的.
,
是等腰三角形.
则③是正确的.
的周长 .
则④是正确的.
二 填空题
13. 如果三角形的三边长 ,,,满足 ,那么这个三角形是直角三角形
14.
15. 直角三角形
16.
17. 等腰直角三角形.
【解析】由题意,得 ,,
,.
是等腰直角三角形.
18. 直角
【解析】提示: .
三 解答题
19. (1) 有两个内角相等的三角形是等腰三角形.
(2) 轴对称图形都是等边三角形.
(3) 四条边相等的图形是正方形.
(4) 如果两个角不是对顶角,那么这两个角不想等.
(5) 面积相等的两个三角形是全等三角形.
20. 原式可变形为 ,
即 ,
,,,
,
为直角三角形.
21. 在 中,,
,
在 中,,
,
22. (1) ;;
【解析】由题意:,,.
故答案为:,,.
(2) 猜想:以 ,, 为边的三角形是直角三角形.
理由:
,,,
,
以 ,, 为边的三角形是直角三角形.
(3)
【解析】观察可知:第五组勾股数为:.
故答案为:.
23. (1) ,,
.
,
.
(2) 在 中,,,,
,
为直角三角形,即 .
,,
.
24. (1) 选思路一:如图①,将 绕点 逆时针旋转 ,得到 ,连接 ,
,
,,,
在 中,,
,
根据勾股定理得,,
,
,
,
,
是直角三角形,且 ,
.
(2) 如图②,将 绕点 逆时针旋转 ,得到 ,连接 ,
,
,,,
在 中,,
,
根据勾股定理得,,
,
,
,
,
是直角三角形,且 ,
.
第1页(共9 页)
