2015年沪科版数学九年级上册单元梯度检测精品卷:(五)第22章相似形单元梯度检测B卷
文档属性
| 名称 | 2015年沪科版数学九年级上册单元梯度检测精品卷:(五)第22章相似形单元梯度检测B卷 |

|
|
| 格式 | zip | ||
| 文件大小 | 426.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-02 00:00:00 | ||
图片预览



文档简介
(五)第22章相似形单元梯度检测B卷
(满分:150分 时间:120分钟)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.若=,则下列比例式:①=;②=;③=;④=.其中正确的有…………………………………………………………【 】
A.1个 B.2个 C.3个 D.4个
2.如图,在△ABC中,DE∥BC,DF∥AC,下列各式中不正确的是…………………【 】
A.== B.==
C.== D.==
3.如图,在△ABC中,DF∥EG∥BC,且AD=DE=EB,记△ADF的面积为S1,梯形DEGF的面积为S2,梯形EBCG的面积为S3,则S1︰S2︰S3的值为………………………【 】
A.1︰2︰3 B. 1︰3︰5 C. 1︰4︰7 D. 2︰5︰8
4.如图,点A、B、C、D、E、甲、乙、丙、丁都是4×4的方格网中的格点,要使以点D、E、F为顶点的三角形与△ABC相似,则点F应是甲、乙、丙、丁四点中的……【 】
A.丙 B.丁 C. 甲或乙 D. 甲或丙
5.如图,△ABC为等边三角形,D、E分别为边BC、CA上一点,BD=5,CE=4,∠ADE=60°,则△ABC的边长为……………………………………………………………【 】
A.25 B.20 C.26 D.15
6.如图,在△ABC中,点D、E分别在边AC、BC上,DE∥AB,AE、BD交于点O,若S△ODE︰S△OBA=4︰25,则的值为………………………………………………【 】
A. B. C. D.
7.如图,线段AB、CD交于点E,F为线段AC上一点,且∠DFB=∠A=∠C ,AB与DF交于点H,CD与BF交于点G,则图中相似三角形有……………………………【 】
A.1对 B.2对 C.3对 D.4对
8.如图,在正方形ABCD中,E为AB边上一点,AE︰EB=2︰1,AF⊥DE于点G,交BC于点F,则△AEG的面积与四边形FCDG的面积之比为………………………【 】
A.1︰9 B. 4︰9 C. 4︰17 D. 5︰17
9.如图,△ABC是一块三角形的铁皮材料,边AB=10cm,BC=6cm,AC=8cm,现要把它加工成正方形铁皮,使正方形的四个顶点均在△ABC的边上,则这个正方形铁皮的边长是………………………………………………………………………………【 】
A.2.4cm B. 2.4cm或
C.cm或cm D. cm或cm
10.如图,在平面直角坐标系中,有正方形ABCD和正方形OEFG,其中A点坐标为(3,2),F点坐标为(﹣1,﹣1),则这两个正方形的位似中心的坐标为………………【 】
A.(1,0) B.(1,0)或(﹣5,﹣2)
C. (2,0) D.(2,0)或(﹣5,﹣2)
二、填空题(本大题共4小题,每小题5分,满分20分)
11.将一个矩形以它的宽为边长截去一个正方形后,剩下的矩形与原矩形相似,则原矩形的长与宽的比为___________.www.21-cn-jy.com
12.在□ABCD中,CD=10,F是AB边上的一点,DF交AC于点E,且AE︰EC=2︰5,连接FC,则=______________. 21*cnjy*com
13.已知菱形ABCD的周长为8,点E在直线AD上,DE=3,直线BE与直线AC交于点F,则=_______________.
14.如图,已知△ABC是的面积为的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE交于点F,则△AEF的面积为____________(结果保留根号).
三、(本大题共两小题,每小题8分,满分16分)
15.已知在四边形ABCD和四边形A′B′C′D′中,====,且四边形ABCD的周长为51cm,求四边形A′B′C′D′的周长.
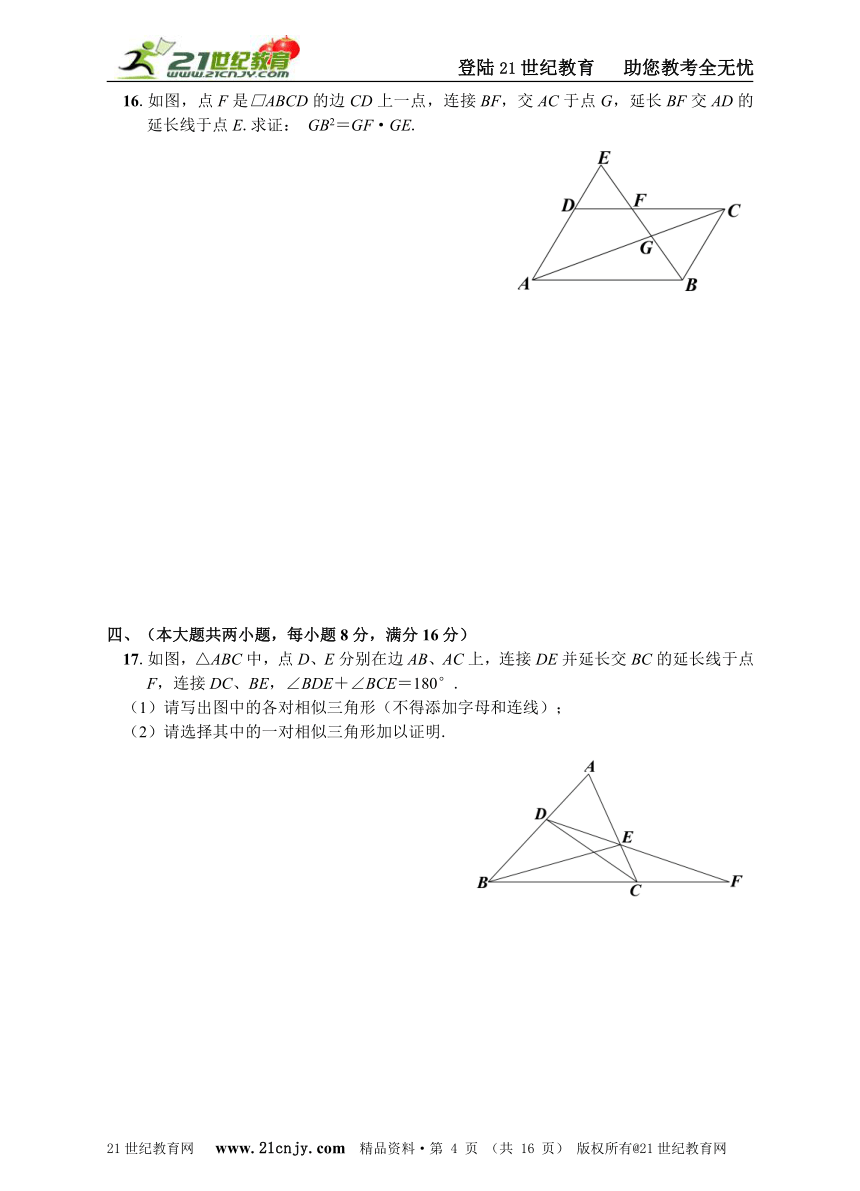
16.如图,点F是□ABCD的边CD上一点,连接BF,交AC于点G,延长BF交AD的延长线于点E.求证: GB2=GF·GE.21·世纪*教育网
四、(本大题共两小题,每小题8分,满分16分)
17.如图,△ABC中,点D、E分别在边AB、AC上,连接DE并延长交BC的延长线于点F,连接DC、BE,∠BDE+∠BCE=180°.【版权所有:21教育】
(1)请写出图中的各对相似三角形(不得添加字母和连线);
(2)请选择其中的一对相似三角形加以证明.
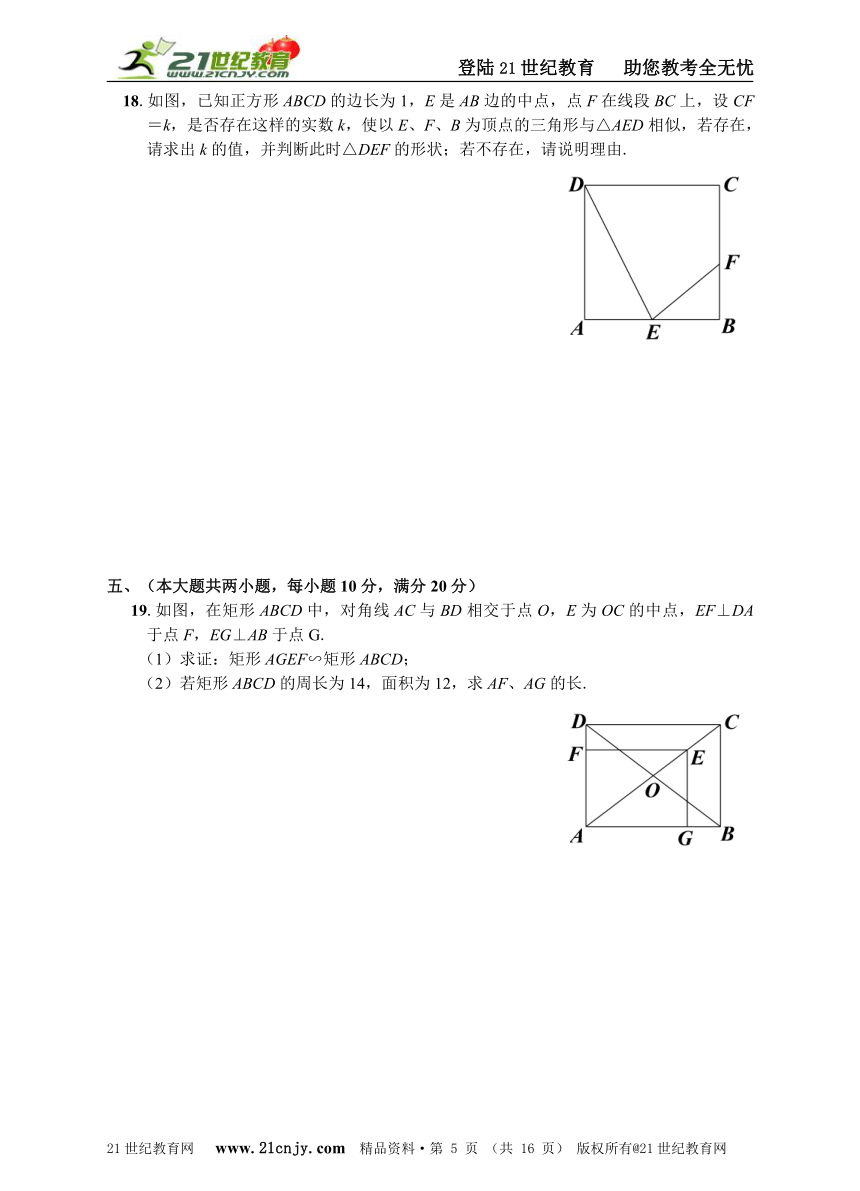
18.如图,已知正方形ABCD的边长为1,E是AB边的中点,点F在线段BC上,设CF=k,是否存在这样的实数k,使以E、F、B为顶点的三角形与△AED相似,若存在,请求出k的值,并判断此时△DEF的形状;若不存在,请说明理由.
五、(本大题共两小题,每小题10分,满分20分)
19.如图,在矩形ABCD中,对角线AC与BD相交于点O,E为OC的中点,EF⊥DA于点F,EG⊥AB于点G.【来源:21cnj*y.co*m】
(1)求证:矩形AGEF∽矩形ABCD;
(2)若矩形ABCD的周长为14,面积为12,求AF、AG的长.
20.如图,△ABC是方格网(每个小正方形的边长均为1)中的格点三角形,已知B(﹣1,3),C(﹣4,2).21教育网
(1)请画出平面直角坐标系,并写出A点坐标;
(2)以原点O为位似中心,位似比为2,在第二象限内将△ABC放大,画出放大后的图形△A′B′C′;
(3)求△A′B′C的面积.
六、(本题满分12分)
21.如图,在△ABC中,D为AB的中点,E为BC上任意一点,AE与CD交于点F,我班毛可同学在探究这一问题时,发现有如下事实:21cnjy.com
当==时,有=,如图1;
当==时,有=,如图2;
当==时,有=,如图3.
在图4中,当=时,参照上述探究结论,请你猜想用n表示的一般结论,并加以证明(n为正整数).
七、(本题满分12分)
22.如图,矩形ABCD中,直线l垂直平分线段BD,垂足为O,直线l分别与线段DC、BA的延长线交于点E、F.2·1·c·n·j·y
(1)求证:=.
(2)试判断四边形DFBE的形状,并说明理由.
八、(本题满分14分)
23.如图,正方形ABCD的边长为4,E、F分别是AB、BC上的两个动点,当E点在AB上运动时,保持DE和EF垂直.2-1-c-n-j-y
(1)证明:Rt△DAE∽Rt△EBF;
(2)设AE=x,梯形DABF的面积为y,求y与x之间的函数关系式;当E点运动到什么位置时,梯形DABF的面积最大,并求出最大面积;21·cn·jy·com
(3)当E点运动到什么位置时,Rt△DAE∽Rt△DEF?请说明理由.
参考答案
1.D 解析:∵=,∴由合比性质可得=,∴①正确;由合比性质得=,∴交换内项得=,∴②正确;由=交换内外项得=,由合比性质得=,又交换内外项得=,∴③正确;由等比性质得=,再由等比性质得=,∴④正确.∴D对.
2.D 解析:∵DE∥BC,DF∥AC,∴四边形ECFD是平行四边形,∴ED=CF,CE=DF,由DE∥BC得=,由DF∥AC得==,∴==,∴①正确;由DE∥BC得=,由DF∥AC得=,∴==,∴②正确;由DF∥AC得=,由DE∥BC得=,∴==,∴③正确;由DF∥AC得=,由DE∥BC得=,∴==,但CE≠DE,∴④错误;∴D对.
∴S△AEG=4 S△ADE=4S1,∵S1+S2=S△AEG,∴S2=3S1,∵AD=DE=EB,∴=,∵DF∥BC,∴△ADF∽△ABC,∴=()2=()2=,∴S△ABC=9S△ADE=9S1,∵S1+S2+S3=S△ABC,S2=3S1,∴S3=5S1,∴S1︰S2︰S3=S1︰3S1︰5S1=1︰3︰5,∴B对. 21世纪教育网版权所有
4.C 解析:若F是丙,则△DEF为等腰直角三角形,而△ABC为钝角三角形,它们不可能相似,∴A错误,D错误;若F是丁,则△DEF为锐角三角形,而△ABC为钝角三角形,它们不可能相似,∴B错误;若F是甲,则DF==,DE==,EF=4,而AB=1,AC==,BC==,∴===,∴△DEF∽△BCA;由整个图形的轴对称性可得,F也可是乙.∴C对. www-2-1-cnjy-com
5.A 解析:∵△ABC为等边三角形,∴AB=BC,∠B=∠C=60°,设△ABC的边长为x,则AB=BC=x,DC=x-5,∵∠ADE=60°,∴∠ADB+∠CDE=120°,又∠ADB+∠BAD=120°,∴∠CDE=∠BAD,∴△CDE∽△BAD,∴=,∴=,解得x=25,∴A对.【出处:21教育名师】
又=,()2=,∴=,又∵DE∥AB,∴△CDE∽△CBA,∴==,∴=,∴B对. 21教育名师原创作品
7.C 解析:∵∠DFB=∠A,∠FBH=∠ABF,∴△FBH∽△ABF;∵∠DFB=∠C,∠FDG=∠CDF,∴△FDG∽△CDF;∵△FDG∽△CDF,∴∠FGD=∠CFD,又∵∠FGD+∠CGF=180°,∠CFD+∠AFH=180°,∴∠CGF=∠AFH,又∠A=∠C,∴△CGF∽△AFH.∴C对.
8.C 解析:∵∠DAB=90°,AF⊥DE,∴∠EAG+∠GAD=∠GAD+∠ADG=90°,∴∠EAG=∠ADG,又∠DAE=∠ABF=90°,DA=AB,∴△DAE∽≌△ABF,∴AE=BF,设EB=x,∵AE︰EB=2︰1,∴AE=BF=2x,AB=3x,在Rt△ABF中,由勾股定理得AF===,∵∠EAG=∠FAB,∠AGE=∠ABF=90°,∴△AGE∽△ABF,∴=()2=()2=,设S△AGE=4a,则S四边形EBFG=9a,∵△DAE∽≌△ABF,∴S四边形EBFG=S△AGD=9a,又S△ABF=×AB×BF,∴×3x×2x=13a,解得x2= a,∴S正方形ABCD=AB2=(3x)2=9 x2=39a,∴S四边形ACDGF=S正方形ABCD―S△AGE―S四边形EBFG―S△AGD=39a―4a―9a―9a=17a,∴==,∴C对.
9.C 解析:∵AB=10,BC=6,AC=8,而62+82=102,∴△ABC为直角三角形,且∠C=90°,分两种情况:当正方形的边落在△ABC的直角边上时,如下图①,设正方形的边长为xcm,由△ADE∽△EFB得=,∴=,解得x=;当正方形的边落在△ABC的斜边上时,如下图②,设正方形的边长为xcm,过点C作CH⊥AB于点H,交DG于点P,由S△ABC=×AB×CH=×AC×CB,∴CH===4.8,∵DG∥AB,则CP⊥DG,由DG∥AB得△CDG∽△CAB,∴=,∴=,解得x=.∴C对.
10.B 解析:当两个正方形反向位似时,如下图①,∵点O与点B对应,∴位似中心M在OB上,由OG∥AB得△OMG∽△BMA,∴=,又=,∴=,又OB=3,∴OM=1,∴M点坐标为(1,0);当两个正方形同向位似时,如下图②,过位似中心M作MN⊥x轴于点N,由EF∥AB得△OEF∽△OAB,∴=,又=,∴=,由EF∥MN 得=,∴=,∴E为NB的中点,又NB=1+3=4,∴NE=4,∴NO=5,由E为NB的中点,EF∥MN 得F为MB的中点,∴MN=2EF=2,又M在第三象限,∴M点坐标为(﹣5,﹣2). ∴B对.
11. 解析:如下图,在矩形ABCD中,四边形BCFE为正方形,设AB=x,AD=y,则EF=y,AE=x-y,由矩形AEFD∽矩形DABC得=,∴=,化简得-1=,设=a,则原方程化为a2-a-1=0,解得a1=,a2=(负值不合题意,舍去),∴=.
12. 解析:∵四边形ABCD是平行四边形,∴AF∥DC,DC=AB,∴△AEF∽△CED,∴=,∵=,CD=10,∴=,∴AF=4,∴FB=AB-AF=10-4=6,∴===.
13.或 解析:分两种情况:当点E在AD的延长线上时,如下图①,∵四边形ABCD是菱形且周长为8,∴AD=BC=2,AE∥BC,∴△AFE∽△CFB,∴=,∵DE=3,∴AE=AD+DE=2+3=5,∴=;当点E在DA的延长线上时,如下图②,∵四边形ABCD是菱形且周长为8,∴AD=BC=2,AE∥BC,∴△AFE∽△CFB,∴=,∵DE=3,∴AE=DE-AD=3-2=1,∴=.∴=或.
14. 解析:如下图,过点C作CG⊥AB于点G,过点F作FH⊥AE于点H,∵△ABC是等边三角形,∴AB=AC,AG=BG,∠CAG=60°,∴由勾股定理得CG==AG=AB,∴S△ABC=×AB×CG==,∴AB=2,∵AB=2AD,∴AD=1,∵△ABC∽△ADE,∴△ADE也为等边三角形,∴AE=1,∠E=∠EAD=60°,∵∠BAD=45°,∴∠EAF=45°,设EH=x,则EF=2x,HF=x=HA,由EH+HA=EA得x+x=1,解得x=,∴HF=x=,∴S△AEF=×AE×FH=×1×=.
15.解:∵====,∴由等比性质得=,∵AB+BC+CD+DA=51,∴=,∴A′B′+B′C′+C′D′+D′A′==85(cm),∴四边形A′B′C′D′的周长为85cm.
16.证明:∵四边形ABCD是平行四边形,∴FC∥AB,∴△FCG∽△BAG,∴=,又BC∥AE,∴△CBG∽△AEG,∴ =,∴=,∴GB2=GF·GE.
17.解:(1)△ADE∽△ACB,△ACD∽△ABE,△FEC∽△FBD,△FCD∽△FEB;
(2)选△ACD∽△ABE,证明:∵∠BDE+∠BCE=180° ,∠BDE+∠ADE=180° ,∴∠ACB(∠BCE)=∠ADE,又∠BAC=∠EAD,∴△ACB∽△ADE,∴=,∴=,又∠CAD=∠BAE,∴△ACD∽△ABE.
18.解:存在;∵四边形ABCD是正方形,∴DA=AB=BC=1,∠A=∠B=90° ,∵E为AB的中点,∴AE=EB=,当△DAE∽△EBF时,则=,∴=,解得BF=,∴CF=BC-BF=1-=,此时△DEF为直角三角形;当△DAE∽△FBE时,则=,∴=,解得BF=1,∴CF=BC-BF=1-1=0,此时点F与点C重合,△DEF为等腰三角形.∴k=0或,当k=0时,△DEF为等腰三角形;当k=时,△DEF为直角三角形.21*cnjy*com
19. 解:(1)∵∠EFA=∠CDA=90°,∴EF∥CD,∴△EFA∽△CDA,∴==,又∵∠EGA=∠CBA=90°,∴EG∥CB,∴△EGA∽△CBA,∴==,∴===,又两个矩形的内角都是直角均相等,∴∠EFA=∠CDA,∠FAG=∠DAB,∠EGA=∠CBA,∠FEG=∠DCB,∴矩形AGEF∽矩形ABCD;
(2)设矩形ABCD的长AB=x,宽AD=y,∵矩形ABCD的周长为14,面积为12,∴可得,解得,∴AB=4,AD=3,由(1)得==,又E为OC中点,AO=CO,∴=,∴==,∴==,解得AF=,AG=3.
20.解:(1)建立平面直角坐标系如下图,A点坐标为(﹣1,1);
(2)放大后的△A′B′C′如下图;
∴=3×4=12.
21.解:猜想:当=时,有=成立;
证明:如下图4,过点D作DG∥AE,交BC于点G,∵AD=BD,∴EG=BG,∴EG=BE,∴==,又=,∴=,∴=,∴=,又∵FE∥DG,∴=,∴=.
22.解:(1)证明:∵DE∥FB,∴∠DEO=∠BFO,∠EDO=∠FBO,又DO=BO,∴△DEO≌△BFO(AAS),∴FO=EO,∵四边形ABCD为矩形,EF⊥DB,∠FOD=∠DAB=90°,∵EF垂直平分BD,∴FD=FB,∴∠FDO=∠DBA,∴△FDO∽△DBA,∴=,∵FO=FE,DO=DB,∴=,∴=;
(2)四边形DFBE为菱形,理由如下:由(1)得△DEO≌△BFO,∴FB=ED,∵EF垂直平分BD,∴FD=FB,ED=EB,∴FD=FB=ED=EB,∴四边形DFBE为菱形.
23.解:(1)∵四边形ABCD是正方形,∴∠A=∠B=90°,∴∠ADE+∠AED=90°,又DE⊥FE,∴∠BEF+∠AED=90°,∴∠ADE=∠BEF,∴Rt△DAE∽Rt△EBF;
(2)由Rt△DAE∽Rt△EBF得=,∴=,解得BF=,∴y=×(BF+DA)×AB=× [(+4)]×4=﹣x2-2x+8=﹣(x-2)2+10,当x=2即E为AB中点时,y最大=10,∴y与x之间的函数关系式为y=﹣x2-2x+8;当E点运动到AB中点时,梯形DABF的面积最大,最大面积为10;【来源:21·世纪·教育·网】
由勾股定理得DE2=AD2+AE2,EF2=BE2+BF2,
∴=,
∴x2(42+x2)=42(4-x) 2+x2(4-x) 2,解得x=2,
当E点运动到AB中点时,Rt△DAE∽Rt△DEF,理由如上.
(满分:150分 时间:120分钟)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.若=,则下列比例式:①=;②=;③=;④=.其中正确的有…………………………………………………………【 】
A.1个 B.2个 C.3个 D.4个
2.如图,在△ABC中,DE∥BC,DF∥AC,下列各式中不正确的是…………………【 】
A.== B.==
C.== D.==
3.如图,在△ABC中,DF∥EG∥BC,且AD=DE=EB,记△ADF的面积为S1,梯形DEGF的面积为S2,梯形EBCG的面积为S3,则S1︰S2︰S3的值为………………………【 】
A.1︰2︰3 B. 1︰3︰5 C. 1︰4︰7 D. 2︰5︰8
4.如图,点A、B、C、D、E、甲、乙、丙、丁都是4×4的方格网中的格点,要使以点D、E、F为顶点的三角形与△ABC相似,则点F应是甲、乙、丙、丁四点中的……【 】
A.丙 B.丁 C. 甲或乙 D. 甲或丙
5.如图,△ABC为等边三角形,D、E分别为边BC、CA上一点,BD=5,CE=4,∠ADE=60°,则△ABC的边长为……………………………………………………………【 】
A.25 B.20 C.26 D.15
6.如图,在△ABC中,点D、E分别在边AC、BC上,DE∥AB,AE、BD交于点O,若S△ODE︰S△OBA=4︰25,则的值为………………………………………………【 】
A. B. C. D.
7.如图,线段AB、CD交于点E,F为线段AC上一点,且∠DFB=∠A=∠C ,AB与DF交于点H,CD与BF交于点G,则图中相似三角形有……………………………【 】
A.1对 B.2对 C.3对 D.4对
8.如图,在正方形ABCD中,E为AB边上一点,AE︰EB=2︰1,AF⊥DE于点G,交BC于点F,则△AEG的面积与四边形FCDG的面积之比为………………………【 】
A.1︰9 B. 4︰9 C. 4︰17 D. 5︰17
9.如图,△ABC是一块三角形的铁皮材料,边AB=10cm,BC=6cm,AC=8cm,现要把它加工成正方形铁皮,使正方形的四个顶点均在△ABC的边上,则这个正方形铁皮的边长是………………………………………………………………………………【 】
A.2.4cm B. 2.4cm或
C.cm或cm D. cm或cm
10.如图,在平面直角坐标系中,有正方形ABCD和正方形OEFG,其中A点坐标为(3,2),F点坐标为(﹣1,﹣1),则这两个正方形的位似中心的坐标为………………【 】
A.(1,0) B.(1,0)或(﹣5,﹣2)
C. (2,0) D.(2,0)或(﹣5,﹣2)
二、填空题(本大题共4小题,每小题5分,满分20分)
11.将一个矩形以它的宽为边长截去一个正方形后,剩下的矩形与原矩形相似,则原矩形的长与宽的比为___________.www.21-cn-jy.com
12.在□ABCD中,CD=10,F是AB边上的一点,DF交AC于点E,且AE︰EC=2︰5,连接FC,则=______________. 21*cnjy*com
13.已知菱形ABCD的周长为8,点E在直线AD上,DE=3,直线BE与直线AC交于点F,则=_______________.
14.如图,已知△ABC是的面积为的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE交于点F,则△AEF的面积为____________(结果保留根号).
三、(本大题共两小题,每小题8分,满分16分)
15.已知在四边形ABCD和四边形A′B′C′D′中,====,且四边形ABCD的周长为51cm,求四边形A′B′C′D′的周长.
16.如图,点F是□ABCD的边CD上一点,连接BF,交AC于点G,延长BF交AD的延长线于点E.求证: GB2=GF·GE.21·世纪*教育网
四、(本大题共两小题,每小题8分,满分16分)
17.如图,△ABC中,点D、E分别在边AB、AC上,连接DE并延长交BC的延长线于点F,连接DC、BE,∠BDE+∠BCE=180°.【版权所有:21教育】
(1)请写出图中的各对相似三角形(不得添加字母和连线);
(2)请选择其中的一对相似三角形加以证明.
18.如图,已知正方形ABCD的边长为1,E是AB边的中点,点F在线段BC上,设CF=k,是否存在这样的实数k,使以E、F、B为顶点的三角形与△AED相似,若存在,请求出k的值,并判断此时△DEF的形状;若不存在,请说明理由.
五、(本大题共两小题,每小题10分,满分20分)
19.如图,在矩形ABCD中,对角线AC与BD相交于点O,E为OC的中点,EF⊥DA于点F,EG⊥AB于点G.【来源:21cnj*y.co*m】
(1)求证:矩形AGEF∽矩形ABCD;
(2)若矩形ABCD的周长为14,面积为12,求AF、AG的长.
20.如图,△ABC是方格网(每个小正方形的边长均为1)中的格点三角形,已知B(﹣1,3),C(﹣4,2).21教育网
(1)请画出平面直角坐标系,并写出A点坐标;
(2)以原点O为位似中心,位似比为2,在第二象限内将△ABC放大,画出放大后的图形△A′B′C′;
(3)求△A′B′C的面积.
六、(本题满分12分)
21.如图,在△ABC中,D为AB的中点,E为BC上任意一点,AE与CD交于点F,我班毛可同学在探究这一问题时,发现有如下事实:21cnjy.com
当==时,有=,如图1;
当==时,有=,如图2;
当==时,有=,如图3.
在图4中,当=时,参照上述探究结论,请你猜想用n表示的一般结论,并加以证明(n为正整数).
七、(本题满分12分)
22.如图,矩形ABCD中,直线l垂直平分线段BD,垂足为O,直线l分别与线段DC、BA的延长线交于点E、F.2·1·c·n·j·y
(1)求证:=.
(2)试判断四边形DFBE的形状,并说明理由.
八、(本题满分14分)
23.如图,正方形ABCD的边长为4,E、F分别是AB、BC上的两个动点,当E点在AB上运动时,保持DE和EF垂直.2-1-c-n-j-y
(1)证明:Rt△DAE∽Rt△EBF;
(2)设AE=x,梯形DABF的面积为y,求y与x之间的函数关系式;当E点运动到什么位置时,梯形DABF的面积最大,并求出最大面积;21·cn·jy·com
(3)当E点运动到什么位置时,Rt△DAE∽Rt△DEF?请说明理由.
参考答案
1.D 解析:∵=,∴由合比性质可得=,∴①正确;由合比性质得=,∴交换内项得=,∴②正确;由=交换内外项得=,由合比性质得=,又交换内外项得=,∴③正确;由等比性质得=,再由等比性质得=,∴④正确.∴D对.
2.D 解析:∵DE∥BC,DF∥AC,∴四边形ECFD是平行四边形,∴ED=CF,CE=DF,由DE∥BC得=,由DF∥AC得==,∴==,∴①正确;由DE∥BC得=,由DF∥AC得=,∴==,∴②正确;由DF∥AC得=,由DE∥BC得=,∴==,∴③正确;由DF∥AC得=,由DE∥BC得=,∴==,但CE≠DE,∴④错误;∴D对.
∴S△AEG=4 S△ADE=4S1,∵S1+S2=S△AEG,∴S2=3S1,∵AD=DE=EB,∴=,∵DF∥BC,∴△ADF∽△ABC,∴=()2=()2=,∴S△ABC=9S△ADE=9S1,∵S1+S2+S3=S△ABC,S2=3S1,∴S3=5S1,∴S1︰S2︰S3=S1︰3S1︰5S1=1︰3︰5,∴B对. 21世纪教育网版权所有
4.C 解析:若F是丙,则△DEF为等腰直角三角形,而△ABC为钝角三角形,它们不可能相似,∴A错误,D错误;若F是丁,则△DEF为锐角三角形,而△ABC为钝角三角形,它们不可能相似,∴B错误;若F是甲,则DF==,DE==,EF=4,而AB=1,AC==,BC==,∴===,∴△DEF∽△BCA;由整个图形的轴对称性可得,F也可是乙.∴C对. www-2-1-cnjy-com
5.A 解析:∵△ABC为等边三角形,∴AB=BC,∠B=∠C=60°,设△ABC的边长为x,则AB=BC=x,DC=x-5,∵∠ADE=60°,∴∠ADB+∠CDE=120°,又∠ADB+∠BAD=120°,∴∠CDE=∠BAD,∴△CDE∽△BAD,∴=,∴=,解得x=25,∴A对.【出处:21教育名师】
又=,()2=,∴=,又∵DE∥AB,∴△CDE∽△CBA,∴==,∴=,∴B对. 21教育名师原创作品
7.C 解析:∵∠DFB=∠A,∠FBH=∠ABF,∴△FBH∽△ABF;∵∠DFB=∠C,∠FDG=∠CDF,∴△FDG∽△CDF;∵△FDG∽△CDF,∴∠FGD=∠CFD,又∵∠FGD+∠CGF=180°,∠CFD+∠AFH=180°,∴∠CGF=∠AFH,又∠A=∠C,∴△CGF∽△AFH.∴C对.
8.C 解析:∵∠DAB=90°,AF⊥DE,∴∠EAG+∠GAD=∠GAD+∠ADG=90°,∴∠EAG=∠ADG,又∠DAE=∠ABF=90°,DA=AB,∴△DAE∽≌△ABF,∴AE=BF,设EB=x,∵AE︰EB=2︰1,∴AE=BF=2x,AB=3x,在Rt△ABF中,由勾股定理得AF===,∵∠EAG=∠FAB,∠AGE=∠ABF=90°,∴△AGE∽△ABF,∴=()2=()2=,设S△AGE=4a,则S四边形EBFG=9a,∵△DAE∽≌△ABF,∴S四边形EBFG=S△AGD=9a,又S△ABF=×AB×BF,∴×3x×2x=13a,解得x2= a,∴S正方形ABCD=AB2=(3x)2=9 x2=39a,∴S四边形ACDGF=S正方形ABCD―S△AGE―S四边形EBFG―S△AGD=39a―4a―9a―9a=17a,∴==,∴C对.
9.C 解析:∵AB=10,BC=6,AC=8,而62+82=102,∴△ABC为直角三角形,且∠C=90°,分两种情况:当正方形的边落在△ABC的直角边上时,如下图①,设正方形的边长为xcm,由△ADE∽△EFB得=,∴=,解得x=;当正方形的边落在△ABC的斜边上时,如下图②,设正方形的边长为xcm,过点C作CH⊥AB于点H,交DG于点P,由S△ABC=×AB×CH=×AC×CB,∴CH===4.8,∵DG∥AB,则CP⊥DG,由DG∥AB得△CDG∽△CAB,∴=,∴=,解得x=.∴C对.
10.B 解析:当两个正方形反向位似时,如下图①,∵点O与点B对应,∴位似中心M在OB上,由OG∥AB得△OMG∽△BMA,∴=,又=,∴=,又OB=3,∴OM=1,∴M点坐标为(1,0);当两个正方形同向位似时,如下图②,过位似中心M作MN⊥x轴于点N,由EF∥AB得△OEF∽△OAB,∴=,又=,∴=,由EF∥MN 得=,∴=,∴E为NB的中点,又NB=1+3=4,∴NE=4,∴NO=5,由E为NB的中点,EF∥MN 得F为MB的中点,∴MN=2EF=2,又M在第三象限,∴M点坐标为(﹣5,﹣2). ∴B对.
11. 解析:如下图,在矩形ABCD中,四边形BCFE为正方形,设AB=x,AD=y,则EF=y,AE=x-y,由矩形AEFD∽矩形DABC得=,∴=,化简得-1=,设=a,则原方程化为a2-a-1=0,解得a1=,a2=(负值不合题意,舍去),∴=.
12. 解析:∵四边形ABCD是平行四边形,∴AF∥DC,DC=AB,∴△AEF∽△CED,∴=,∵=,CD=10,∴=,∴AF=4,∴FB=AB-AF=10-4=6,∴===.
13.或 解析:分两种情况:当点E在AD的延长线上时,如下图①,∵四边形ABCD是菱形且周长为8,∴AD=BC=2,AE∥BC,∴△AFE∽△CFB,∴=,∵DE=3,∴AE=AD+DE=2+3=5,∴=;当点E在DA的延长线上时,如下图②,∵四边形ABCD是菱形且周长为8,∴AD=BC=2,AE∥BC,∴△AFE∽△CFB,∴=,∵DE=3,∴AE=DE-AD=3-2=1,∴=.∴=或.
14. 解析:如下图,过点C作CG⊥AB于点G,过点F作FH⊥AE于点H,∵△ABC是等边三角形,∴AB=AC,AG=BG,∠CAG=60°,∴由勾股定理得CG==AG=AB,∴S△ABC=×AB×CG==,∴AB=2,∵AB=2AD,∴AD=1,∵△ABC∽△ADE,∴△ADE也为等边三角形,∴AE=1,∠E=∠EAD=60°,∵∠BAD=45°,∴∠EAF=45°,设EH=x,则EF=2x,HF=x=HA,由EH+HA=EA得x+x=1,解得x=,∴HF=x=,∴S△AEF=×AE×FH=×1×=.
15.解:∵====,∴由等比性质得=,∵AB+BC+CD+DA=51,∴=,∴A′B′+B′C′+C′D′+D′A′==85(cm),∴四边形A′B′C′D′的周长为85cm.
16.证明:∵四边形ABCD是平行四边形,∴FC∥AB,∴△FCG∽△BAG,∴=,又BC∥AE,∴△CBG∽△AEG,∴ =,∴=,∴GB2=GF·GE.
17.解:(1)△ADE∽△ACB,△ACD∽△ABE,△FEC∽△FBD,△FCD∽△FEB;
(2)选△ACD∽△ABE,证明:∵∠BDE+∠BCE=180° ,∠BDE+∠ADE=180° ,∴∠ACB(∠BCE)=∠ADE,又∠BAC=∠EAD,∴△ACB∽△ADE,∴=,∴=,又∠CAD=∠BAE,∴△ACD∽△ABE.
18.解:存在;∵四边形ABCD是正方形,∴DA=AB=BC=1,∠A=∠B=90° ,∵E为AB的中点,∴AE=EB=,当△DAE∽△EBF时,则=,∴=,解得BF=,∴CF=BC-BF=1-=,此时△DEF为直角三角形;当△DAE∽△FBE时,则=,∴=,解得BF=1,∴CF=BC-BF=1-1=0,此时点F与点C重合,△DEF为等腰三角形.∴k=0或,当k=0时,△DEF为等腰三角形;当k=时,△DEF为直角三角形.21*cnjy*com
19. 解:(1)∵∠EFA=∠CDA=90°,∴EF∥CD,∴△EFA∽△CDA,∴==,又∵∠EGA=∠CBA=90°,∴EG∥CB,∴△EGA∽△CBA,∴==,∴===,又两个矩形的内角都是直角均相等,∴∠EFA=∠CDA,∠FAG=∠DAB,∠EGA=∠CBA,∠FEG=∠DCB,∴矩形AGEF∽矩形ABCD;
(2)设矩形ABCD的长AB=x,宽AD=y,∵矩形ABCD的周长为14,面积为12,∴可得,解得,∴AB=4,AD=3,由(1)得==,又E为OC中点,AO=CO,∴=,∴==,∴==,解得AF=,AG=3.
20.解:(1)建立平面直角坐标系如下图,A点坐标为(﹣1,1);
(2)放大后的△A′B′C′如下图;
∴=3×4=12.
21.解:猜想:当=时,有=成立;
证明:如下图4,过点D作DG∥AE,交BC于点G,∵AD=BD,∴EG=BG,∴EG=BE,∴==,又=,∴=,∴=,∴=,又∵FE∥DG,∴=,∴=.
22.解:(1)证明:∵DE∥FB,∴∠DEO=∠BFO,∠EDO=∠FBO,又DO=BO,∴△DEO≌△BFO(AAS),∴FO=EO,∵四边形ABCD为矩形,EF⊥DB,∠FOD=∠DAB=90°,∵EF垂直平分BD,∴FD=FB,∴∠FDO=∠DBA,∴△FDO∽△DBA,∴=,∵FO=FE,DO=DB,∴=,∴=;
(2)四边形DFBE为菱形,理由如下:由(1)得△DEO≌△BFO,∴FB=ED,∵EF垂直平分BD,∴FD=FB,ED=EB,∴FD=FB=ED=EB,∴四边形DFBE为菱形.
23.解:(1)∵四边形ABCD是正方形,∴∠A=∠B=90°,∴∠ADE+∠AED=90°,又DE⊥FE,∴∠BEF+∠AED=90°,∴∠ADE=∠BEF,∴Rt△DAE∽Rt△EBF;
(2)由Rt△DAE∽Rt△EBF得=,∴=,解得BF=,∴y=×(BF+DA)×AB=× [(+4)]×4=﹣x2-2x+8=﹣(x-2)2+10,当x=2即E为AB中点时,y最大=10,∴y与x之间的函数关系式为y=﹣x2-2x+8;当E点运动到AB中点时,梯形DABF的面积最大,最大面积为10;【来源:21·世纪·教育·网】
由勾股定理得DE2=AD2+AE2,EF2=BE2+BF2,
∴=,
∴x2(42+x2)=42(4-x) 2+x2(4-x) 2,解得x=2,
当E点运动到AB中点时,Rt△DAE∽Rt△DEF,理由如上.
