北师大版七下第二章《相交线与平行线》单元测试卷(含解析)
文档属性
| 名称 | 北师大版七下第二章《相交线与平行线》单元测试卷(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-10 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第一章整式的乘除单元测试卷
时间100分钟 满分120分
姓名 班级 编号
一、选择题(每小题3分,共36分)
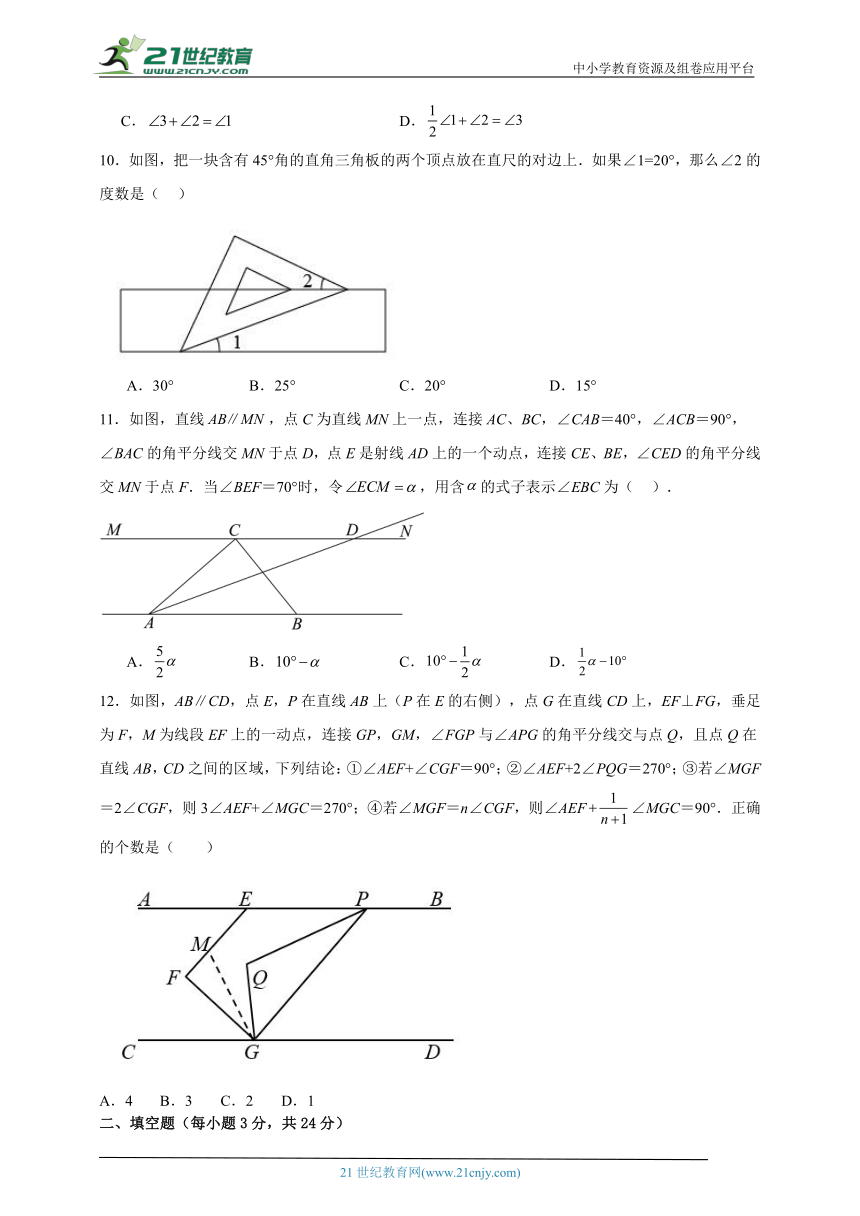
1.如图,在测量跳远成绩的示意图中,直线l是起跳线,则需要测量的线段是( )
A. B. C. D.
2.如图,能与构成同位角的有( )
A.4个 B.3个 C.2个 D.1个
3.如图,把一块含直角三角板的直角面点放在直尺的一边上,如果,那么的度数是( )
A. B. C. D.
4.下列说法中,不正确的是( )
A.经过一点能画一条直线和已知线段垂直
B.一条直线可以有无数条垂线
C.过射线的端点与该射线垂直的直线有且只有一条
D.过直线外一点并过直线上一点可画一条直线与该直线垂直
5.如图分别平分则图中与相等的角(不含它本身)的个数是( )
A. B. C. D.
6.如图所示,,,,,则等于( )
A. B. C. D.不能确定
7.如图△ABC中,∠A=60°,点D、E、F分别是BC、AB、AC上的点,且DE∥AC,DF∥AB,则∠EDF的大小为 ( )
A.150° B.120° C.60° D.30°
8.下列说法不正确的是( )
A.一个时钟在它显示8:30时,时针与分针所成的角度是75°
B.如果两个角是对顶角,那么这两个角相等
C.用放大镜看一个角,角的度数变大了
D.若,,,则有
9.如图,若直线那么与之间的数量关系是( )
A. B.
C. D.
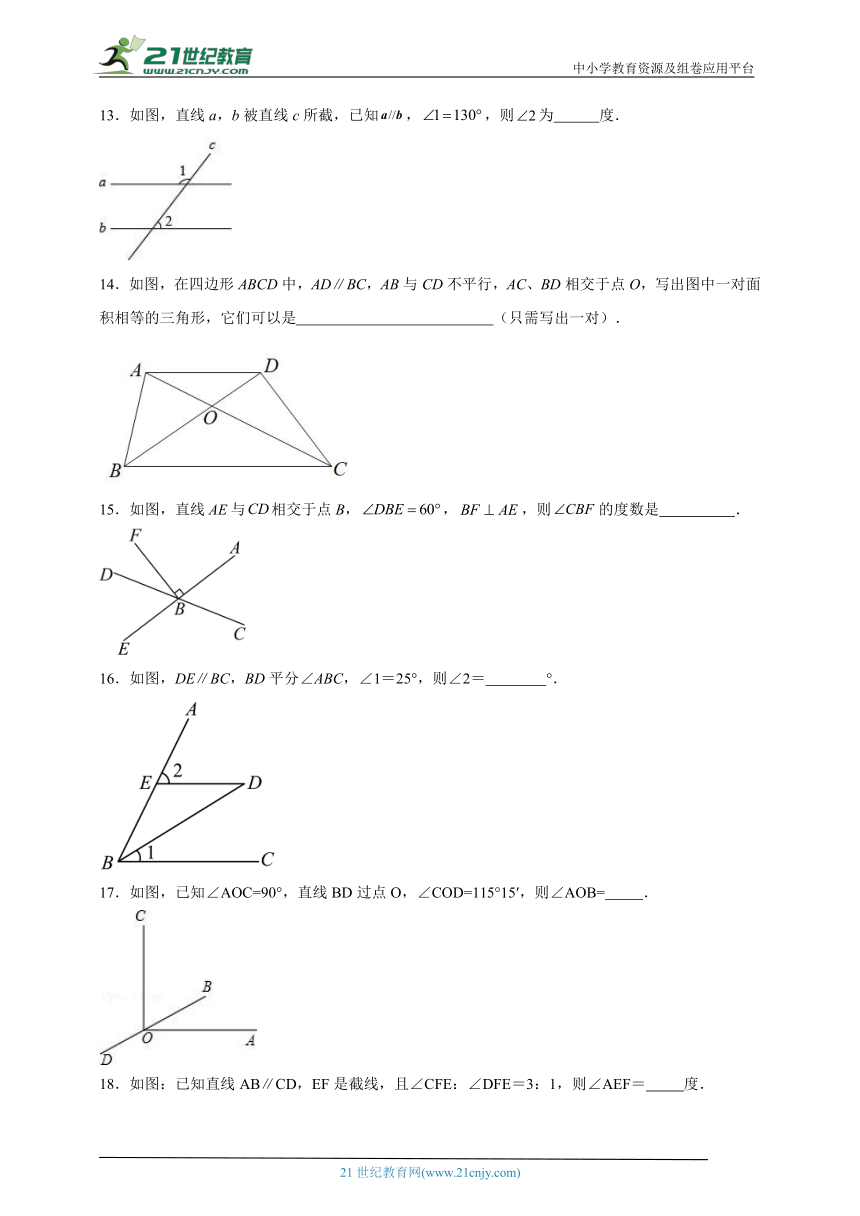
10.如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
A.30° B.25° C.20° D.15°
11.如图,直线,点C为直线MN上一点,连接AC、BC,∠CAB=40°,∠ACB=90°,∠BAC的角平分线交MN于点D,点E是射线AD上的一个动点,连接CE、BE,∠CED的角平分线交MN于点F.当∠BEF=70°时,令,用含的式子表示∠EBC为( ).
A. B. C. D.
12.如图,AB∥CD,点E,P在直线AB上(P在E的右侧),点G在直线CD上,EF⊥FG,垂足为F,M为线段EF上的一动点,连接GP,GM,∠FGP与∠APG的角平分线交与点Q,且点Q在直线AB,CD之间的区域,下列结论:①∠AEF+∠CGF=90°;②∠AEF+2∠PQG=270°;③若∠MGF=2∠CGF,则3∠AEF+∠MGC=270°;④若∠MGF=n∠CGF,则∠AEF∠MGC=90°.正确的个数是( )
A.4 B.3 C.2 D.1
二、填空题(每小题3分,共24分)
13.如图,直线a,b被直线c所截,已知,,则为 度.
14.如图,在四边形ABCD中,AD∥BC,AB与CD不平行,AC、BD相交于点O,写出图中一对面积相等的三角形,它们可以是 (只需写出一对).
15.如图,直线与相交于点B,,,则的度数是 .
16.如图,DE∥BC,BD平分∠ABC,∠1=25°,则∠2= °.
17.如图,已知∠AOC=90°,直线BD过点O,∠COD=115°15′,则∠AOB= .
18.如图:已知直线AB∥CD,EF是截线,且∠CFE:∠DFE=3:1,则∠AEF= 度.
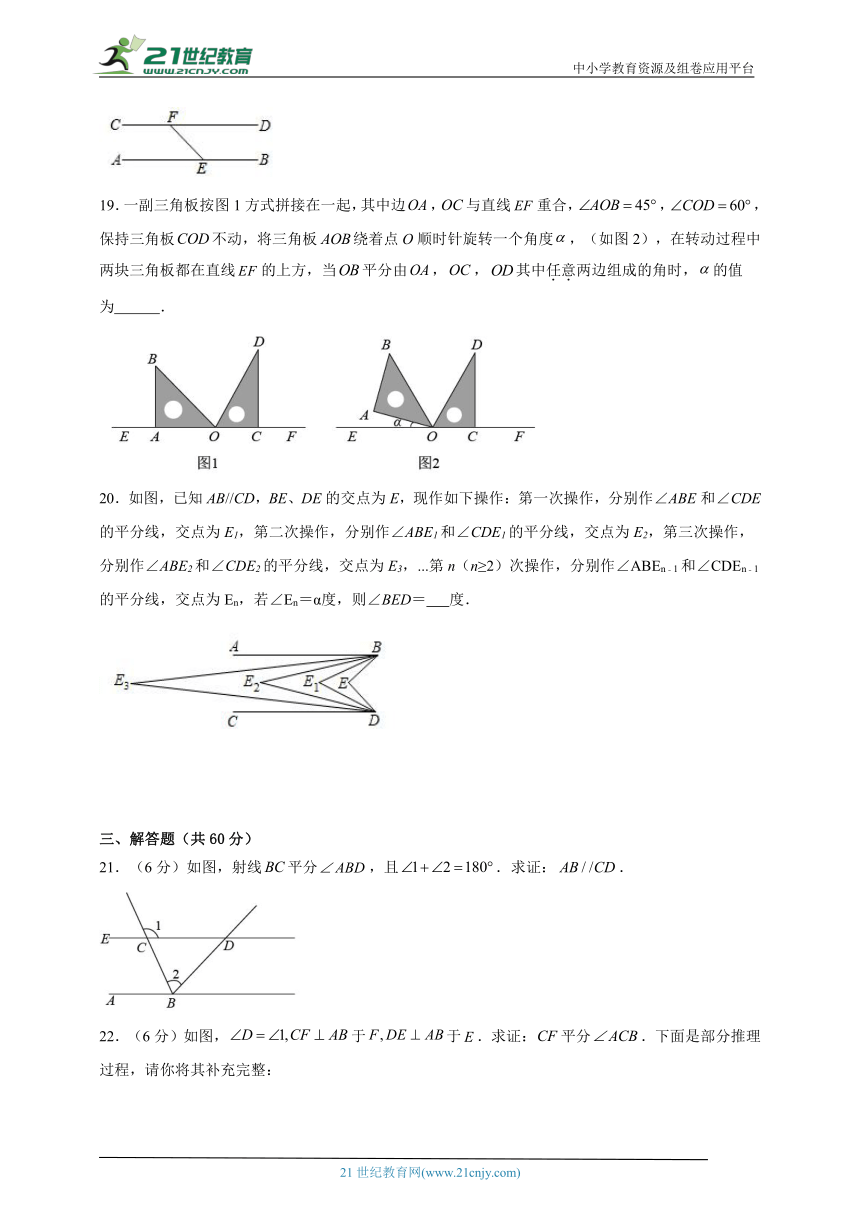
19.一副三角板按图1方式拼接在一起,其中边,与直线重合,,,保持三角板不动,将三角板绕着点O顺时针旋转一个角度,(如图2),在转动过程中两块三角板都在直线的上方,当平分由,,其中任意两边组成的角时,的值为 .
20.如图,已知AB//CD,BE、DE的交点为E,现作如下操作:第一次操作,分别作∠ABE和∠CDE的平分线,交点为E1,第二次操作,分别作∠ABE1和∠CDE1的平分线,交点为E2,第三次操作,分别作∠ABE2和∠CDE2的平分线,交点为E3,...第n(n≥2)次操作,分别作∠ABEn﹣1和∠CDEn﹣1的平分线,交点为En,若∠En=α度,则∠BED= 度.
三、解答题(共60分)
21.(6分)如图,射线平分,且.求证:.
22.(6分)如图,于于.求证:平分.下面是部分推理过程,请你将其补充完整:
于于(已知)
( )
( )
且( )( )
又(已知)
( )
平分( )
23.(12分)如图,,CE平分∠BCF,,,.
(1)求证:∥;
(2)求,的度数.
24.(8分)已知:如图,AB∥CD,∠1=∠2,求证:∠B=∠D.
证明:∵∠1=∠2(已知)
∴ ( )
∴∠BAD+∠B=180°( )
又∵AB∥CD(已知)
∴ + =180°( )
∴∠B=∠D( )
25.(10分)(1)问题发现:如图①,直线,连结,可以发现
请把下面的证明过程补充完整:
证明:过点作,
∴(______).
∵(已知),.
∴(______).
∴.
∵(______).
∴.(等量代换).
(2)拓展探究:如果点运动到图②所示的位置,其他条件不变,说明:.
(3)解决问题:如图③,,是与之间的点,直接写出,,之间的数量关系.
26.(8分)已知:平分,求证:平分.
27.(10分)(1)将直角三角形ABC(∠C为直角)按如图1放置,使得坐标原点与点C重合,已知A(a,3),B(b,-3),且a+b=8,求三角形ACB的面积:
(2)将直角三角形ACB(∠C为直角)按如图2方式放置,使得点O在边AC上,D是y轴上一点,过D作DF//x轴,交AB于F点,AB交x轴于点G, BC交DF于点E, 若∠AOG=50°,求∠BEF的度数.
将直角三角形ACB(∠C为直角)按照如图3方式放置,使得∠C在x轴于DF之间,N为AC边上一点,且∠NEC+∠CEF=180°,写出∠NEF与∠AOG之间的数量关系,并证明你的结论.
第二章单元测试卷参考答案
1.B[提示:根据垂线段最短可得,需要测量的线段是,
故选:B.]
2.B[提示:如图,与能构成同位角的有:∠1,∠2,∠3.
故选B.]
3.B[提示:
∵ab,
∴∠2=∠3,
∵∠1=38°,∠3+∠1=90°,
∵∠3=52°,
∴∠2=∠3=52°,
故选B.]
4.D[提示A. 经过一点能画一条直线和已知线段垂直,正确;
B. 一条直线可以有无数条垂线,正确;
C. 过射线的端点与该射线垂直的直线有且只有一条,正确;
D. 过直线外一点并过直线上一点不一定能画一条直线与该直线垂直,故错误.
故选D.]
5.C[提示:如图,做如下标记,
∵,
∴(两直线平行,内错角相等),
又∵分别平分
∴,
又∵,,(对顶角相等),
∴=(等量替换)
故与相等的角有7个,
故C为答案.]
6.B[提示:,,
,
又,
,
故选:.]
7.C[提示:因为DE∥AC,DF∥AB,所以四边形AEDF是平行四边形,则∠EDF=∠A=60°.
故选C.]
8.C[提示:A、8:30,分针对准的是数字6,分针从数字8又转动30分,也就是30×0.5°=15°,所以夹角是60°+15°=75°,故选项A正确,不符合题意;
B、对顶角相等,故选项B正确,不符合题意;
C、放大镜看一个角,角的度数不会变.故选项C错误,符合题意;
D、∵∠C=20.15°=20°9′,∴∠A>∠C>∠B,故选项D正确,不符合题意.
故选:C.]
9.A[提示:如图过点G做FE∥
∵FE∥
∴∠1=∠BGE,∠2=∠DGE,
∵∠BGE+∠DGE=∠3,
∴,
故选A.]
10.B[提示:∵直尺的对边互相平行,
∴∠1=∠3,
∵∠3+∠2=45°,
∴∠1+∠2=45°,
∵∠1=20°,
∴∠2=45°﹣∠1=25°,
故选:B.]
11.D[提示:在△ABC中,∠CAB=40°,∠ACB=90°,
∴∠ABC=50°.
延长CE,交AB于点G,
∵,
∴,∠ACM=∠BAC=40°,
∴∠ACE=-40°,
∴∠BCE=90°-(-40°)=130°-.
∵∠CEA=180°-∠CAE-∠ACE,
∴∠CED=180°-∠CEA=∠CAE+∠ACE=20°+(-40°)=-20°.
∵EF平分∠CED,
∴∠CEF=,
∴∠CEB=,
∴∠EBC=.
故选:D.]
12.A[提示:①过点F作FH∥AB,如图:
∵AB∥CD,∴AB∥FH∥CD,
∴∠AEF=∠EFH,∠CGF=∠GFH,
∵EF⊥FG,即∠EFG=∠EFH+∠GFH=90°,
∴∠AEF+∠CGF=90°,故①正确;
②∵AB∥CD,PQ平分∠APG,GQ平分∠FGP,
∴∠APQ=∠2,∠FGQ=∠1,
∴∠3=∠APQ+∠2=2∠2,
∠CGF+∠FGQ+∠1+∠3=∠CGF+2∠1+∠3=180°,
即2∠1=180°-2∠2-∠CGF,
∴2∠2+2∠1=180°-∠CGF,
∵∠PQG=180°-(∠2+∠1),
∴2∠PQG=360°-2(∠2+∠1)= 360°-(180°-∠CGF)= 180°+∠CGF,
∴∠AEF+2∠PQG=∠AEF+180°+∠CGF=180°+90°=270°,故②正确;
③∵∠MGF=2∠CGF,
∴∠MGC=3∠CGF,
∴3∠AEF+∠MGC=3∠AEF+3∠CGF=3(∠AEF+∠CGF)= 390°=270°;
3∠AEF+∠MGC=270°,故③正确;
④∵∠MGF=n∠CGF,
∴∠MGC=(n+1)∠CGF,即∠CGF=∠MGC,
∵∠AEF+∠CGF=90°,
∴∠AEF∠MGC=90°,故④正确.
综上,①②③④都正确,共4个,
故选:A.]
13.50[提示:如图,
∵,,
∴∠3=130°,
又∵∠2+∠3=180°,
∴∠2=180°-∠3=180°-130°=50°.
故答案为:50.]
14.△ABC和△DBC(答案不唯一)[提示:∵AD∥BC,
∴AD与BC之间的距离相等,
∴△ABC和△DBC面积相等.
故答案为:△ABC和△DBC.(答案不唯一)]
15.[提示:,
.
与是对顶角,
.
由角的和差,得
,
故答案为:]
16.50[提示:∵BD平分∠ABC,∠1=25°
∴
∵DE∥BC,
∴
故答案为:50.]
17.25°15′[提示:∵∠COD+∠COB=180°,∠COD=115°15′,
∴∠COB=180°﹣115°15′=64°45′,
∴∠AOB=90°﹣∠COB=25°15′.
故答案为25°15′.]
18.45[提示:∵∠CFE:∠DFE=3:1,
∴∠DFE=180°×=45°,
∵AB∥CD,
∴∠AEF=45°.
故答案为:45.]
19.或或[提示:①当在左边且平分时,
∵,,
∴;
②当在右边且平分时,
∵,
∴,
∵,
∴,
∴;
③当在右边且平分时,
∵,
∴,
∴,
综上所述的值为或或.]
20.[提示:如下图,过作,
∵,
∴,
∴,
∵,
∴;
如下图,
∵和的平分线交点为
∴
∵和的平分线交点为,
∴;
∵和的平分线交点为,
∴;
…
以此类推,
∴当度时,度.
故答案为 .]
21.证明:∵平分(已知)
∴(角平分线的定义)
∵(对顶角相等)
又∵(已知)
∴(等量代换)
∴(同旁内角互补,两直线平行)
22.解:于于(已知)
(同一平面内,垂直于同一条直线的两条直线平行)
(两直线平行,内错角相等)
且( )(两直线平行,同位角相等)
又(已知)
(等量代换)
平分(角平分线的定义)
23.解:(1)证明:∵∠DAC+∠ACB=180°,
∴BC∥AD,
∵CE平分∠BCF,
∴∠ECB=∠FCE,
∵∠FEC=∠FCE,
∴∠FEC=∠BCE,
∴BC∥EF,
∴AD∥EF;
(2)设∠BCE=∠ECF=∠BCF=x.
由∠DAC=3∠BCF可得出∠DAC=6x,
则6x+x+x+20°=180°,
解得x=20°,
则∠DAC的度数为120°,∠FEC的度数为20°.
24.解:∵∠1=∠2(已知)
∴ AD BC ( 内错角相等,两直线平行 )
∴∠BAD+∠B= 180° (两直线平行,同旁内角互补)
又∵AB∥CD(已知)
∴ ∠BAD + ∠D =180° (两直线平行,同旁内角互补)
∴∠B=∠D (同角的补角相等)
25.(1)证明:过点作,
∴(_两直线平行,内错角相等_____).
∵(已知),.
∴(__平行于同一条直线的两条直线互相平行____).
∴.
∵(______).
∴.(等量代换)
(2)证明:∵过做
∴
∵
∴
∴
∴
∴
∵
∴
(3)解:理由如下:
过点作,过作,过作
∴,,,
∴,,
∴,,,
∴
26.证明:∵平分,
∴,
∵,
∴,,,
∴,
∴平分.
27.(1)作AM⊥y轴与M,作BN⊥y轴于N,
∴=
=
过C作CM//x轴,∴∠ACM =∠AOG=50°,
而∠BEF=∠CED=∠MCE
∴∠BEF=∠ACB-∠ACM =40°
(3)过C作CM//x轴,设∠NEC=x,∠NEF=y,∠AOG= z
∵∠NEC+∠CEF=180°, 而∠NEC+∠NEF+∠BEF=180°,
∴∠NEC=∠BEF= x
∴∠NEF+2∠NEC=180°,即2 x+ y=180°, ①
∵∠BEF=∠CED=∠MCE= x,∠AOG=∠ACM= z
∴∠ACB=∠ACM+∠MCE= 90°, 即x+z=90°, ②
①-②×2, 得:y=2 z
∴∠NEF=2∠AOG
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第一章整式的乘除单元测试卷
时间100分钟 满分120分
姓名 班级 编号
一、选择题(每小题3分,共36分)
1.如图,在测量跳远成绩的示意图中,直线l是起跳线,则需要测量的线段是( )
A. B. C. D.
2.如图,能与构成同位角的有( )
A.4个 B.3个 C.2个 D.1个
3.如图,把一块含直角三角板的直角面点放在直尺的一边上,如果,那么的度数是( )
A. B. C. D.
4.下列说法中,不正确的是( )
A.经过一点能画一条直线和已知线段垂直
B.一条直线可以有无数条垂线
C.过射线的端点与该射线垂直的直线有且只有一条
D.过直线外一点并过直线上一点可画一条直线与该直线垂直
5.如图分别平分则图中与相等的角(不含它本身)的个数是( )
A. B. C. D.
6.如图所示,,,,,则等于( )
A. B. C. D.不能确定
7.如图△ABC中,∠A=60°,点D、E、F分别是BC、AB、AC上的点,且DE∥AC,DF∥AB,则∠EDF的大小为 ( )
A.150° B.120° C.60° D.30°
8.下列说法不正确的是( )
A.一个时钟在它显示8:30时,时针与分针所成的角度是75°
B.如果两个角是对顶角,那么这两个角相等
C.用放大镜看一个角,角的度数变大了
D.若,,,则有
9.如图,若直线那么与之间的数量关系是( )
A. B.
C. D.
10.如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
A.30° B.25° C.20° D.15°
11.如图,直线,点C为直线MN上一点,连接AC、BC,∠CAB=40°,∠ACB=90°,∠BAC的角平分线交MN于点D,点E是射线AD上的一个动点,连接CE、BE,∠CED的角平分线交MN于点F.当∠BEF=70°时,令,用含的式子表示∠EBC为( ).
A. B. C. D.
12.如图,AB∥CD,点E,P在直线AB上(P在E的右侧),点G在直线CD上,EF⊥FG,垂足为F,M为线段EF上的一动点,连接GP,GM,∠FGP与∠APG的角平分线交与点Q,且点Q在直线AB,CD之间的区域,下列结论:①∠AEF+∠CGF=90°;②∠AEF+2∠PQG=270°;③若∠MGF=2∠CGF,则3∠AEF+∠MGC=270°;④若∠MGF=n∠CGF,则∠AEF∠MGC=90°.正确的个数是( )
A.4 B.3 C.2 D.1
二、填空题(每小题3分,共24分)
13.如图,直线a,b被直线c所截,已知,,则为 度.
14.如图,在四边形ABCD中,AD∥BC,AB与CD不平行,AC、BD相交于点O,写出图中一对面积相等的三角形,它们可以是 (只需写出一对).
15.如图,直线与相交于点B,,,则的度数是 .
16.如图,DE∥BC,BD平分∠ABC,∠1=25°,则∠2= °.
17.如图,已知∠AOC=90°,直线BD过点O,∠COD=115°15′,则∠AOB= .
18.如图:已知直线AB∥CD,EF是截线,且∠CFE:∠DFE=3:1,则∠AEF= 度.
19.一副三角板按图1方式拼接在一起,其中边,与直线重合,,,保持三角板不动,将三角板绕着点O顺时针旋转一个角度,(如图2),在转动过程中两块三角板都在直线的上方,当平分由,,其中任意两边组成的角时,的值为 .
20.如图,已知AB//CD,BE、DE的交点为E,现作如下操作:第一次操作,分别作∠ABE和∠CDE的平分线,交点为E1,第二次操作,分别作∠ABE1和∠CDE1的平分线,交点为E2,第三次操作,分别作∠ABE2和∠CDE2的平分线,交点为E3,...第n(n≥2)次操作,分别作∠ABEn﹣1和∠CDEn﹣1的平分线,交点为En,若∠En=α度,则∠BED= 度.
三、解答题(共60分)
21.(6分)如图,射线平分,且.求证:.
22.(6分)如图,于于.求证:平分.下面是部分推理过程,请你将其补充完整:
于于(已知)
( )
( )
且( )( )
又(已知)
( )
平分( )
23.(12分)如图,,CE平分∠BCF,,,.
(1)求证:∥;
(2)求,的度数.
24.(8分)已知:如图,AB∥CD,∠1=∠2,求证:∠B=∠D.
证明:∵∠1=∠2(已知)
∴ ( )
∴∠BAD+∠B=180°( )
又∵AB∥CD(已知)
∴ + =180°( )
∴∠B=∠D( )
25.(10分)(1)问题发现:如图①,直线,连结,可以发现
请把下面的证明过程补充完整:
证明:过点作,
∴(______).
∵(已知),.
∴(______).
∴.
∵(______).
∴.(等量代换).
(2)拓展探究:如果点运动到图②所示的位置,其他条件不变,说明:.
(3)解决问题:如图③,,是与之间的点,直接写出,,之间的数量关系.
26.(8分)已知:平分,求证:平分.
27.(10分)(1)将直角三角形ABC(∠C为直角)按如图1放置,使得坐标原点与点C重合,已知A(a,3),B(b,-3),且a+b=8,求三角形ACB的面积:
(2)将直角三角形ACB(∠C为直角)按如图2方式放置,使得点O在边AC上,D是y轴上一点,过D作DF//x轴,交AB于F点,AB交x轴于点G, BC交DF于点E, 若∠AOG=50°,求∠BEF的度数.
将直角三角形ACB(∠C为直角)按照如图3方式放置,使得∠C在x轴于DF之间,N为AC边上一点,且∠NEC+∠CEF=180°,写出∠NEF与∠AOG之间的数量关系,并证明你的结论.
第二章单元测试卷参考答案
1.B[提示:根据垂线段最短可得,需要测量的线段是,
故选:B.]
2.B[提示:如图,与能构成同位角的有:∠1,∠2,∠3.
故选B.]
3.B[提示:
∵ab,
∴∠2=∠3,
∵∠1=38°,∠3+∠1=90°,
∵∠3=52°,
∴∠2=∠3=52°,
故选B.]
4.D[提示A. 经过一点能画一条直线和已知线段垂直,正确;
B. 一条直线可以有无数条垂线,正确;
C. 过射线的端点与该射线垂直的直线有且只有一条,正确;
D. 过直线外一点并过直线上一点不一定能画一条直线与该直线垂直,故错误.
故选D.]
5.C[提示:如图,做如下标记,
∵,
∴(两直线平行,内错角相等),
又∵分别平分
∴,
又∵,,(对顶角相等),
∴=(等量替换)
故与相等的角有7个,
故C为答案.]
6.B[提示:,,
,
又,
,
故选:.]
7.C[提示:因为DE∥AC,DF∥AB,所以四边形AEDF是平行四边形,则∠EDF=∠A=60°.
故选C.]
8.C[提示:A、8:30,分针对准的是数字6,分针从数字8又转动30分,也就是30×0.5°=15°,所以夹角是60°+15°=75°,故选项A正确,不符合题意;
B、对顶角相等,故选项B正确,不符合题意;
C、放大镜看一个角,角的度数不会变.故选项C错误,符合题意;
D、∵∠C=20.15°=20°9′,∴∠A>∠C>∠B,故选项D正确,不符合题意.
故选:C.]
9.A[提示:如图过点G做FE∥
∵FE∥
∴∠1=∠BGE,∠2=∠DGE,
∵∠BGE+∠DGE=∠3,
∴,
故选A.]
10.B[提示:∵直尺的对边互相平行,
∴∠1=∠3,
∵∠3+∠2=45°,
∴∠1+∠2=45°,
∵∠1=20°,
∴∠2=45°﹣∠1=25°,
故选:B.]
11.D[提示:在△ABC中,∠CAB=40°,∠ACB=90°,
∴∠ABC=50°.
延长CE,交AB于点G,
∵,
∴,∠ACM=∠BAC=40°,
∴∠ACE=-40°,
∴∠BCE=90°-(-40°)=130°-.
∵∠CEA=180°-∠CAE-∠ACE,
∴∠CED=180°-∠CEA=∠CAE+∠ACE=20°+(-40°)=-20°.
∵EF平分∠CED,
∴∠CEF=,
∴∠CEB=,
∴∠EBC=.
故选:D.]
12.A[提示:①过点F作FH∥AB,如图:
∵AB∥CD,∴AB∥FH∥CD,
∴∠AEF=∠EFH,∠CGF=∠GFH,
∵EF⊥FG,即∠EFG=∠EFH+∠GFH=90°,
∴∠AEF+∠CGF=90°,故①正确;
②∵AB∥CD,PQ平分∠APG,GQ平分∠FGP,
∴∠APQ=∠2,∠FGQ=∠1,
∴∠3=∠APQ+∠2=2∠2,
∠CGF+∠FGQ+∠1+∠3=∠CGF+2∠1+∠3=180°,
即2∠1=180°-2∠2-∠CGF,
∴2∠2+2∠1=180°-∠CGF,
∵∠PQG=180°-(∠2+∠1),
∴2∠PQG=360°-2(∠2+∠1)= 360°-(180°-∠CGF)= 180°+∠CGF,
∴∠AEF+2∠PQG=∠AEF+180°+∠CGF=180°+90°=270°,故②正确;
③∵∠MGF=2∠CGF,
∴∠MGC=3∠CGF,
∴3∠AEF+∠MGC=3∠AEF+3∠CGF=3(∠AEF+∠CGF)= 390°=270°;
3∠AEF+∠MGC=270°,故③正确;
④∵∠MGF=n∠CGF,
∴∠MGC=(n+1)∠CGF,即∠CGF=∠MGC,
∵∠AEF+∠CGF=90°,
∴∠AEF∠MGC=90°,故④正确.
综上,①②③④都正确,共4个,
故选:A.]
13.50[提示:如图,
∵,,
∴∠3=130°,
又∵∠2+∠3=180°,
∴∠2=180°-∠3=180°-130°=50°.
故答案为:50.]
14.△ABC和△DBC(答案不唯一)[提示:∵AD∥BC,
∴AD与BC之间的距离相等,
∴△ABC和△DBC面积相等.
故答案为:△ABC和△DBC.(答案不唯一)]
15.[提示:,
.
与是对顶角,
.
由角的和差,得
,
故答案为:]
16.50[提示:∵BD平分∠ABC,∠1=25°
∴
∵DE∥BC,
∴
故答案为:50.]
17.25°15′[提示:∵∠COD+∠COB=180°,∠COD=115°15′,
∴∠COB=180°﹣115°15′=64°45′,
∴∠AOB=90°﹣∠COB=25°15′.
故答案为25°15′.]
18.45[提示:∵∠CFE:∠DFE=3:1,
∴∠DFE=180°×=45°,
∵AB∥CD,
∴∠AEF=45°.
故答案为:45.]
19.或或[提示:①当在左边且平分时,
∵,,
∴;
②当在右边且平分时,
∵,
∴,
∵,
∴,
∴;
③当在右边且平分时,
∵,
∴,
∴,
综上所述的值为或或.]
20.[提示:如下图,过作,
∵,
∴,
∴,
∵,
∴;
如下图,
∵和的平分线交点为
∴
∵和的平分线交点为,
∴;
∵和的平分线交点为,
∴;
…
以此类推,
∴当度时,度.
故答案为 .]
21.证明:∵平分(已知)
∴(角平分线的定义)
∵(对顶角相等)
又∵(已知)
∴(等量代换)
∴(同旁内角互补,两直线平行)
22.解:于于(已知)
(同一平面内,垂直于同一条直线的两条直线平行)
(两直线平行,内错角相等)
且( )(两直线平行,同位角相等)
又(已知)
(等量代换)
平分(角平分线的定义)
23.解:(1)证明:∵∠DAC+∠ACB=180°,
∴BC∥AD,
∵CE平分∠BCF,
∴∠ECB=∠FCE,
∵∠FEC=∠FCE,
∴∠FEC=∠BCE,
∴BC∥EF,
∴AD∥EF;
(2)设∠BCE=∠ECF=∠BCF=x.
由∠DAC=3∠BCF可得出∠DAC=6x,
则6x+x+x+20°=180°,
解得x=20°,
则∠DAC的度数为120°,∠FEC的度数为20°.
24.解:∵∠1=∠2(已知)
∴ AD BC ( 内错角相等,两直线平行 )
∴∠BAD+∠B= 180° (两直线平行,同旁内角互补)
又∵AB∥CD(已知)
∴ ∠BAD + ∠D =180° (两直线平行,同旁内角互补)
∴∠B=∠D (同角的补角相等)
25.(1)证明:过点作,
∴(_两直线平行,内错角相等_____).
∵(已知),.
∴(__平行于同一条直线的两条直线互相平行____).
∴.
∵(______).
∴.(等量代换)
(2)证明:∵过做
∴
∵
∴
∴
∴
∴
∵
∴
(3)解:理由如下:
过点作,过作,过作
∴,,,
∴,,
∴,,,
∴
26.证明:∵平分,
∴,
∵,
∴,,,
∴,
∴平分.
27.(1)作AM⊥y轴与M,作BN⊥y轴于N,
∴=
=
过C作CM//x轴,∴∠ACM =∠AOG=50°,
而∠BEF=∠CED=∠MCE
∴∠BEF=∠ACB-∠ACM =40°
(3)过C作CM//x轴,设∠NEC=x,∠NEF=y,∠AOG= z
∵∠NEC+∠CEF=180°, 而∠NEC+∠NEF+∠BEF=180°,
∴∠NEC=∠BEF= x
∴∠NEF+2∠NEC=180°,即2 x+ y=180°, ①
∵∠BEF=∠CED=∠MCE= x,∠AOG=∠ACM= z
∴∠ACB=∠ACM+∠MCE= 90°, 即x+z=90°, ②
①-②×2, 得:y=2 z
∴∠NEF=2∠AOG
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
