第17章勾股定理 单元达标测试题(含解析) 人教版八年级数学下册
文档属性
| 名称 | 第17章勾股定理 单元达标测试题(含解析) 人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 345.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-10 20:03:23 | ||
图片预览



文档简介
人教版八年级数学下册《第17章勾股定理》单元达标测试题
一、单选题(满分32分)
1.下列各组数中,以它们为边长能构成直角三角形的是( )
A.1,3,3 B.2,3,4 C.6,8,9 D.5,12,13
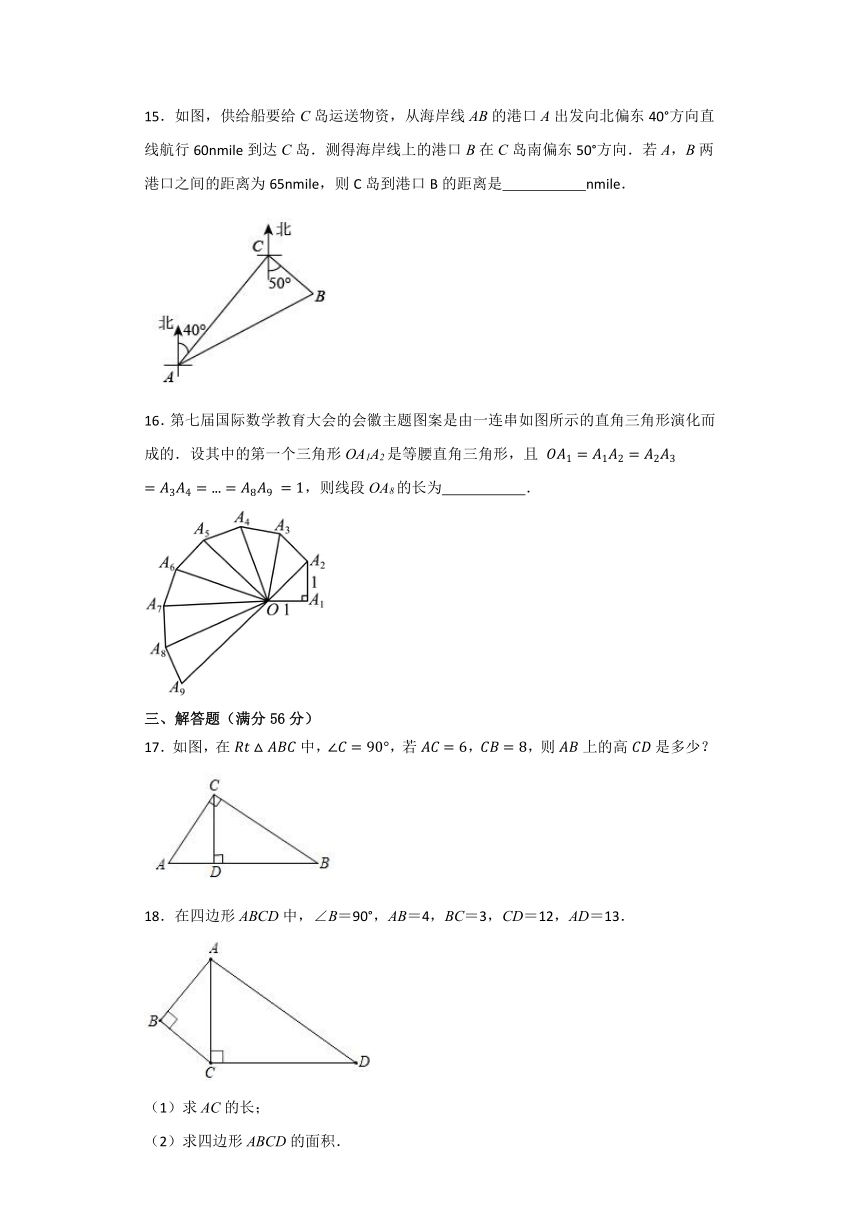
2.一个直角三角形的两条直角边长分别为和,那么此三角形的斜边长为( )
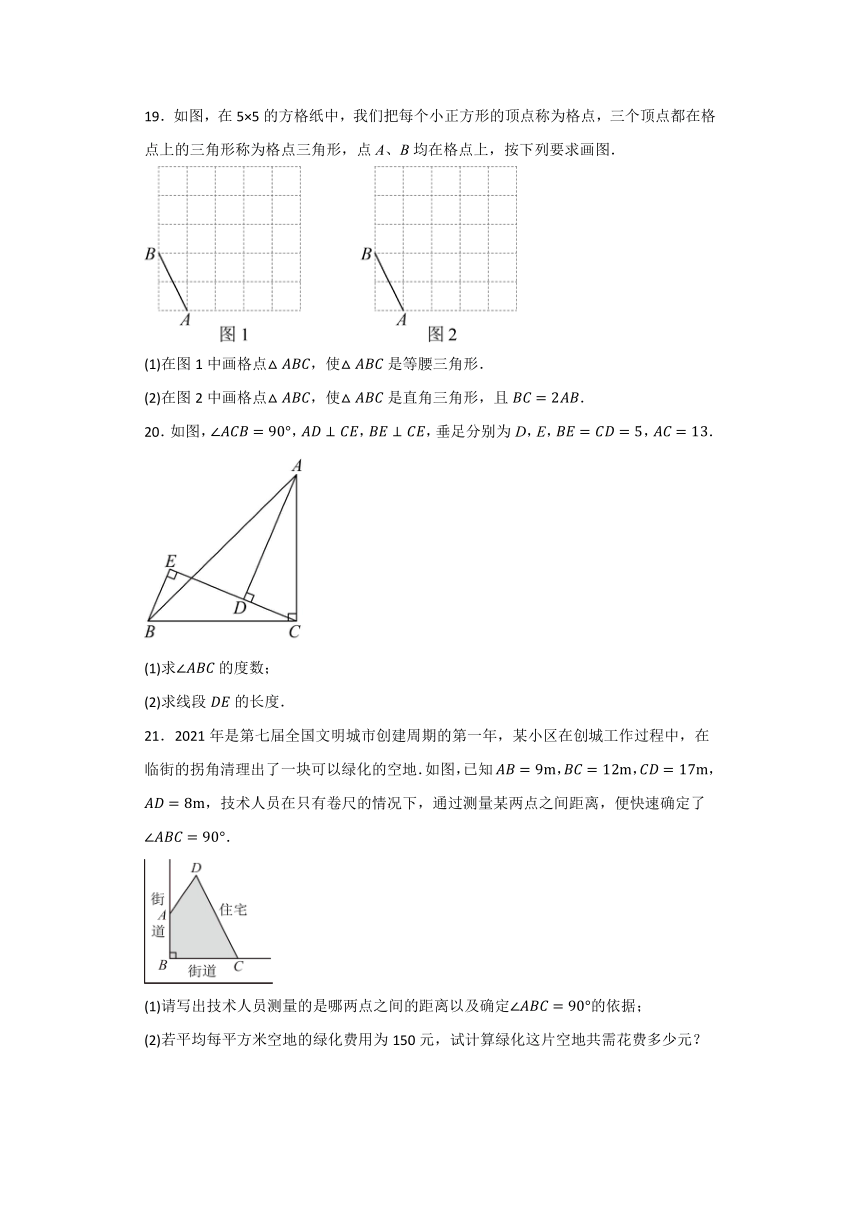
A. B. C.或 D.
3.等腰三角形的腰长为,底边上的中线长为,它的面积是( )
A. B. C. D.
4.如图,一块边长米的正方形绿地四周被小路环绕,点B在正方形的边上,则居民从比从A沿直线直接到B处要多走( )
A.5米 B.米 C.米 D.6米
5.如图,一段与水平面成30°角的斜坡上有两棵树,两棵树水平距离为,树的高度都是.一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞 .( )
A. B.8 C.11 D.12
6.一架5m的梯子,斜靠在一竖直的墙上,这时梯子的底端距墙角4m,若梯子的顶端下滑1m,则梯子的底端将滑动( )
A.0m B.1m C. D.
7.如图,在数轴上点所表示的数分别为,,以点为圆心,的长为半径画弧,交数轴于点(点在点的右侧),则点所表示的数是( )
A. B. C. D.
8.如图,在中,于点于点交于点,已知,则( )
A.1 B.2 C.3 D.4
二、填空题(满分32分)
9.在平面直角坐标系中,点到原点的距离为 .
10.在中,斜边,则 .
11.已知直角三角形面积为24,斜边长为10,则其周长为 .
12.如图 中,,垂足为 ,若 ,,,则 的长是 .
13.如图,每个小正方形边长都为1,连接小正方形的三个顶点,,,可得,则边上的高为 .
14.如图所示,已知中,,,于,为上任一点,则等于 .
15.如图,供给船要给C岛运送物资,从海岸线AB的港口A出发向北偏东40°方向直线航行60nmile到达C岛.测得海岸线上的港口B在C岛南偏东50°方向.若A,B两港口之间的距离为65nmile,则C岛到港口B的距离是 nmile.
16.第七届国际数学教育大会的会徽主题图案是由一连串如图所示的直角三角形演化而成的.设其中的第一个三角形OA1A2是等腰直角三角形,且 ,则线段OA8的长为 .
三、解答题(满分56分)
17.如图,在中,,若,,则上的高是多少?
18.在四边形ABCD中,∠B=90°,AB=4,BC=3,CD=12,AD=13.
(1)求AC的长;
(2)求四边形ABCD的面积.
19.如图,在5×5的方格纸中,我们把每个小正方形的顶点称为格点,三个顶点都在格点上的三角形称为格点三角形,点A、B均在格点上,按下列要求画图.
(1)在图1中画格点,使是等腰三角形.
(2)在图2中画格点,使是直角三角形,且.
20.如图,,,,垂足分别为D,E,,.
(1)求的度数;
(2)求线段的长度.
21.2021年是第七届全国文明城市创建周期的第一年,某小区在创城工作过程中,在临街的拐角清理出了一块可以绿化的空地.如图,已知,,,,技术人员在只有卷尺的情况下,通过测量某两点之间距离,便快速确定了.
(1)请写出技术人员测量的是哪两点之间的距离以及确定的依据;
(2)若平均每平方米空地的绿化费用为150元,试计算绿化这片空地共需花费多少元?
22.已知中,,点从点出发,以每秒1个单位的速度沿着折线运动,运动到点停止.
(1)在点运动过程中,当与的周长相等时,求此时的值;
(2)当为何值时,?
(3)当为何值时,是以为底的等腰三角形?
23.(1)如图,的平分线交于点E,D为边上一点,且满足.
①求证:;
②若,,,求的长.
(2)在长方形的边上取一点E,将沿翻折,使点C恰好落在边上点F处.
①如图1,若,求的度数;
②如图2,当,,求的长.
参考答案
1.解:A、,不能构成直角三角形,不符合题意;
B、,不能构成直角三角形,不符合题意;
C、,不能构成直角三角形,不符合题意;
D、,能构成直角三角形,符合题意;
故选D.
2.解:一个直角三角形的两条直角边长分别为和,
此三角形的斜边长为:,
故选:B.
3.解:如图,∵,为底边上的中线,
∴,
∴,
∴,
∴,
∴,
故选:D.
4.解:由正方形的性质得:米,米
∴(米),
∴(米),
即居民从比从A沿直线直接到B处要多走6米,
故选:D.
5.解:根据题意,,,,
∴,,
∴m,
∴m,
∴小鸟至少要飞,
故选:.
6.解:由题意画出图形如下:
在中,,,
,
在中,,,
,
,
即梯子的底端将滑动,
故选:D.
7.解:如图:,
∴,
∴点D所表示的数是
故选:D
8.解:∵,
∴,
∵
在中,由勾股定理得:
在和中,
,
∴
∴,
∴,
故选:B.
9.解:由勾股定理知,.
故答案为:
10.解:∵在中,斜边
∴
∴
故答案为:2.
11.解:设直角三角形的两直角边分别是a、b(,且a、b均为正数),
则,
解得:,
所以该直角三角形的周长是:.
故答案为:24.
12.解:∵,,
∴,
∵,,
∴在中,,
在中,,
故答案为:.
13.解:依题意,,
,
∴边上的高为,
故答案为:.
14.解:∵于,
∴,
在和中,
,,
在和中,
,
,
,
.
故答案为:.
15.解:根据题意可知,
∴.
在中,,,
∴(nmile).
故答案为:25.
16.解:∵ ,图中所有三角形都是直角三角形,根据勾股定理可得:,,,,,,,
故答案为:.
17.解:Rt△ABC中,∵∠C=90°,AC=6,CB=8,
∴由勾股定理,得.
由面积公式,得,即,
∴.
18.解:(1)∵∠B=90°,AB=4,BC=3,
∴;
(2)由(1)知,AC=5,
∵CD=12,AD=13,
∴AC2+CD2=AD2,
∴是直角三角形,∠ACD=90°,
∵AB=4,BC=3,∠B=90°,AC=5,CD=12,∠ACD=90°,
∴四边形ABCD的面积是,
即四边形ABCD的面积是36.
19.(1)解:如图所示,即为所求(答案不唯一);
(2)如图所示,即为所求;
由图可知:,
∴,
即:是直角三角形,且.
20.解:(1)∵,,
∴,
∵,
∴,
∵,
∴,
在和中,
,
∴,
∴,
∵,
∴
(2)∵,,.
∴,
∵,
∴,
∴.
21.(1)解:测量的是点,之间的距离;
依据是:如果三角形的三边长,,满足,那么这个三角形是直角三角形.
(2)如图,连接,
,,,
,
由勾股定理,得,
又,,
,
是直角三角形,
.
.
绿化费用为:(元).
答:绿化这片空地共需要元.
22.(1)解:由题意得:,则,
则,
解得:,
答:当与的周长相等时,;
(2)解:当时,,
,,
,即,
解得:;
(3)解:当点在线段上时,
由(2)可知:当时,,
当时,,
当点在线段上、时,
,
,
,
综上所述:当或16时,是以为底的等腰三角形.
23.解:(1)①∵平分,
∴,
又,
∴,
∴;
②∵平分,
∴,
∵,
∴,,
∴,
∴;
(2)∵,,
∴,
∵翻折,
∴,
又,
∴;
②∵翻折,
∴,,
∵,,
∴,
∴,
在中,,
∴,
∴,
解得.
一、单选题(满分32分)
1.下列各组数中,以它们为边长能构成直角三角形的是( )
A.1,3,3 B.2,3,4 C.6,8,9 D.5,12,13
2.一个直角三角形的两条直角边长分别为和,那么此三角形的斜边长为( )
A. B. C.或 D.
3.等腰三角形的腰长为,底边上的中线长为,它的面积是( )
A. B. C. D.
4.如图,一块边长米的正方形绿地四周被小路环绕,点B在正方形的边上,则居民从比从A沿直线直接到B处要多走( )
A.5米 B.米 C.米 D.6米
5.如图,一段与水平面成30°角的斜坡上有两棵树,两棵树水平距离为,树的高度都是.一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞 .( )
A. B.8 C.11 D.12
6.一架5m的梯子,斜靠在一竖直的墙上,这时梯子的底端距墙角4m,若梯子的顶端下滑1m,则梯子的底端将滑动( )
A.0m B.1m C. D.
7.如图,在数轴上点所表示的数分别为,,以点为圆心,的长为半径画弧,交数轴于点(点在点的右侧),则点所表示的数是( )
A. B. C. D.
8.如图,在中,于点于点交于点,已知,则( )
A.1 B.2 C.3 D.4
二、填空题(满分32分)
9.在平面直角坐标系中,点到原点的距离为 .
10.在中,斜边,则 .
11.已知直角三角形面积为24,斜边长为10,则其周长为 .
12.如图 中,,垂足为 ,若 ,,,则 的长是 .
13.如图,每个小正方形边长都为1,连接小正方形的三个顶点,,,可得,则边上的高为 .
14.如图所示,已知中,,,于,为上任一点,则等于 .
15.如图,供给船要给C岛运送物资,从海岸线AB的港口A出发向北偏东40°方向直线航行60nmile到达C岛.测得海岸线上的港口B在C岛南偏东50°方向.若A,B两港口之间的距离为65nmile,则C岛到港口B的距离是 nmile.
16.第七届国际数学教育大会的会徽主题图案是由一连串如图所示的直角三角形演化而成的.设其中的第一个三角形OA1A2是等腰直角三角形,且 ,则线段OA8的长为 .
三、解答题(满分56分)
17.如图,在中,,若,,则上的高是多少?
18.在四边形ABCD中,∠B=90°,AB=4,BC=3,CD=12,AD=13.
(1)求AC的长;
(2)求四边形ABCD的面积.
19.如图,在5×5的方格纸中,我们把每个小正方形的顶点称为格点,三个顶点都在格点上的三角形称为格点三角形,点A、B均在格点上,按下列要求画图.
(1)在图1中画格点,使是等腰三角形.
(2)在图2中画格点,使是直角三角形,且.
20.如图,,,,垂足分别为D,E,,.
(1)求的度数;
(2)求线段的长度.
21.2021年是第七届全国文明城市创建周期的第一年,某小区在创城工作过程中,在临街的拐角清理出了一块可以绿化的空地.如图,已知,,,,技术人员在只有卷尺的情况下,通过测量某两点之间距离,便快速确定了.
(1)请写出技术人员测量的是哪两点之间的距离以及确定的依据;
(2)若平均每平方米空地的绿化费用为150元,试计算绿化这片空地共需花费多少元?
22.已知中,,点从点出发,以每秒1个单位的速度沿着折线运动,运动到点停止.
(1)在点运动过程中,当与的周长相等时,求此时的值;
(2)当为何值时,?
(3)当为何值时,是以为底的等腰三角形?
23.(1)如图,的平分线交于点E,D为边上一点,且满足.
①求证:;
②若,,,求的长.
(2)在长方形的边上取一点E,将沿翻折,使点C恰好落在边上点F处.
①如图1,若,求的度数;
②如图2,当,,求的长.
参考答案
1.解:A、,不能构成直角三角形,不符合题意;
B、,不能构成直角三角形,不符合题意;
C、,不能构成直角三角形,不符合题意;
D、,能构成直角三角形,符合题意;
故选D.
2.解:一个直角三角形的两条直角边长分别为和,
此三角形的斜边长为:,
故选:B.
3.解:如图,∵,为底边上的中线,
∴,
∴,
∴,
∴,
∴,
故选:D.
4.解:由正方形的性质得:米,米
∴(米),
∴(米),
即居民从比从A沿直线直接到B处要多走6米,
故选:D.
5.解:根据题意,,,,
∴,,
∴m,
∴m,
∴小鸟至少要飞,
故选:.
6.解:由题意画出图形如下:
在中,,,
,
在中,,,
,
,
即梯子的底端将滑动,
故选:D.
7.解:如图:,
∴,
∴点D所表示的数是
故选:D
8.解:∵,
∴,
∵
在中,由勾股定理得:
在和中,
,
∴
∴,
∴,
故选:B.
9.解:由勾股定理知,.
故答案为:
10.解:∵在中,斜边
∴
∴
故答案为:2.
11.解:设直角三角形的两直角边分别是a、b(,且a、b均为正数),
则,
解得:,
所以该直角三角形的周长是:.
故答案为:24.
12.解:∵,,
∴,
∵,,
∴在中,,
在中,,
故答案为:.
13.解:依题意,,
,
∴边上的高为,
故答案为:.
14.解:∵于,
∴,
在和中,
,,
在和中,
,
,
,
.
故答案为:.
15.解:根据题意可知,
∴.
在中,,,
∴(nmile).
故答案为:25.
16.解:∵ ,图中所有三角形都是直角三角形,根据勾股定理可得:,,,,,,,
故答案为:.
17.解:Rt△ABC中,∵∠C=90°,AC=6,CB=8,
∴由勾股定理,得.
由面积公式,得,即,
∴.
18.解:(1)∵∠B=90°,AB=4,BC=3,
∴;
(2)由(1)知,AC=5,
∵CD=12,AD=13,
∴AC2+CD2=AD2,
∴是直角三角形,∠ACD=90°,
∵AB=4,BC=3,∠B=90°,AC=5,CD=12,∠ACD=90°,
∴四边形ABCD的面积是,
即四边形ABCD的面积是36.
19.(1)解:如图所示,即为所求(答案不唯一);
(2)如图所示,即为所求;
由图可知:,
∴,
即:是直角三角形,且.
20.解:(1)∵,,
∴,
∵,
∴,
∵,
∴,
在和中,
,
∴,
∴,
∵,
∴
(2)∵,,.
∴,
∵,
∴,
∴.
21.(1)解:测量的是点,之间的距离;
依据是:如果三角形的三边长,,满足,那么这个三角形是直角三角形.
(2)如图,连接,
,,,
,
由勾股定理,得,
又,,
,
是直角三角形,
.
.
绿化费用为:(元).
答:绿化这片空地共需要元.
22.(1)解:由题意得:,则,
则,
解得:,
答:当与的周长相等时,;
(2)解:当时,,
,,
,即,
解得:;
(3)解:当点在线段上时,
由(2)可知:当时,,
当时,,
当点在线段上、时,
,
,
,
综上所述:当或16时,是以为底的等腰三角形.
23.解:(1)①∵平分,
∴,
又,
∴,
∴;
②∵平分,
∴,
∵,
∴,,
∴,
∴;
(2)∵,,
∴,
∵翻折,
∴,
又,
∴;
②∵翻折,
∴,,
∵,,
∴,
∴,
在中,,
∴,
∴,
解得.
