陕西省西安市碑林区重点中学2023-2024学年七年级下学期开学数学试卷(含解析)
文档属性
| 名称 | 陕西省西安市碑林区重点中学2023-2024学年七年级下学期开学数学试卷(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 428.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-10 20:45:33 | ||
图片预览




文档简介
2023-2024学年陕西省西安市碑林区重点中学七年级(下)开学数学试卷
一、选择题
1.(3分)﹣3的绝对值的相反数是( )
A.﹣3 B.3 C. D.
2.(3分)截至2022年5月4日,我国31个省(自治区、直辖市)和新疆生产建设兵团累计报告接种新冠病毒疫苗约3350000000剂次,将3350000000用科学记数法表示为( )
A.335×107 B.33.5×108
C.3.35×109 D.0.335×1010
3.(3分)下列图形旋转一周,能得到如图几何体的是( )
A. B. C. D.
4.(3分)下列调查中,最适合采用全面调查(普查)的是( )
A.调查全国中小学生对第二次太空授课的满意度
B.调查全国人民,掌握新冠防疫知识情况
C.了解某类型医用口罩的质量
D.检查神舟飞船十三号的各零部件
5.(3分)下列可以表示37.48°的是( )
A.37°12′36″ B.37°12′38″ C.37°26′38″ D.37°28′48″
6.(3分)代数式﹣0.3x,0,2m2n3﹣5m4,,,,﹣2a2b2c,中单项式有( )
A.5个 B.6个 C.7个 D.8个
7.(3分)以∠AOB的顶点O为端点引射线OC,使∠AOC:∠BOC=5:4,若∠AOB=27°,则∠AOC为( )
A.15或108° B.12或135°
C.15°或135° D.以上答案都不正确
8.(3分)某工程甲独做需8天完成,乙独做需10天完成.现在由甲先做3天,然后甲和乙合作共同完成.若设完成此项工程共需x天,则下列方程正确的是( )
A.+ B.+
C.+ D.+
9.(3分)观察下列一组图形,其中图形①中共有2颗星,图形②中共有6颗星,图形③中共有11颗星,图形④中共有17颗星,.按此规律,图形⑨中星星的颗数是( )
A.51 B.53 C.61 D.62
10.(3分)a是不为2的有理数,我们把称为a的“哈利数”.如:3的“哈利数”是=﹣2,﹣2的“哈利数”是=,已知a1=5,a2是a1的“哈利数”,a3是a2的“哈利数”,a4是a3的“哈利数”,…,依此类推,则a2022等于( )
A. B.﹣ C. D.5
二、填空题
11.(3分)一架直升机从高度为500米的位置开始,先以20米/秒的速度垂直上升50秒,再以12米/秒的速度垂直下降100秒,这时飞机所在的高度是 米.
12.(3分)单项式与2y3x3的和仍是单项式,则(m+n)2023= .
13.(3分)如图,已知C,D两点将线段AB分为三部分,且AC:CD:DB=2:3:4.若AB的中点为M,BD的中点为N,且MN=5cm,则AD= .
14.(3分)若3m2+4m﹣6的值为9,则的值为 .
15.(3分)已知等式(m﹣3)x|m|﹣2+5=0是关于x的一元一次方程,则m3= .
16.(3分)有理数a,b,c,满足|a+b+c|=a+b﹣c,且c≠0,则|a+b﹣c+3|﹣|c﹣6|= .
三、解答题
17.计算:
(1)(﹣3)×(﹣4)+(﹣2)3÷4;
(2);
(3)5(x+8)﹣5=6(4x﹣8);
(4).
18.先化简,再求值:已知(a﹣1)2+|b+2|=0,求代数式(6a2﹣2ab)﹣2的值.
19.为进一步加强学生“学党史、知党情、跟党走”的信心,培养学生的民族精神和爱国主义情怀,某学校组织开展以“观看红色电影,点燃红色初心”为主题的教育活动.电影票价格表如下:
购票张数 1至40 41至80 80以上
每张票的价格 20元 18元 免2张门票,其余每张17元
该校七年级两个班共有83名学生去看电影,其中七(1)班的学生人数超过30,但不足40.
(1)如果两个班都以班为单位单独购票,一共付了1572元.求七(2)班学生的人数;
(2)在(1)所得的班级学生人数下,如果七(1)班有7名学生因有比赛任务不能参加这次活动,请你为两个班级设计购买电影票的方案,并指出最省钱的方案.
20.某班学生列队从学校到一个农场去参加劳动,以每小时4千米的速度行进.走完1千米时,一个学生奉命回学校取一件东西,他以每小时5千米的速度跑回学校,取了东西后又立即以同样的速度跑步追赶队伍,结果在距农场1.5千米的地方追上队伍,求学校到农场的距离.
21.规定:若关于x的一元一次方程ax+b=0的解为x=a+b,则称该方程是“奇异方程”.例如:的解为,因为,所以该方程是“奇异方程”.
(1)若关于x的一元一次方程3x+m=0是“奇异方程”,则m的值为 .
(2)若关于x的一元一次方程2x+mn+m=0和﹣2x+mn+n=0都是“奇异方程”,则代数式18(mn+m)2﹣(mn+n)2的值为 .
22.钟表是我们日常生活中常用的计时工具.在圆形钟面上,把一周等分成12个大格,每个大格等分成5个小格.如图,设在4:00时,分针的位置为OB,时针的位置为OA,运动后的分针为OP,时针为OQ(本题中的角均指小于180°的角).若在4:00至5:00之间,OM在∠AOP内,ON在∠AOQ内,,.
(1)当OP在∠AOB内时,求∠POM和∠AON之间的数量关系;
(2)从4:00开始几分钟后,∠MON=111°.(直接写答案)
参考答案与试题解析
一、选择题
1.(3分)﹣3的绝对值的相反数是( )
A.﹣3 B.3 C. D.
【解答】解:﹣3的绝对值为:|﹣3|=3,
3的相反数为:﹣3,
所以﹣3的绝对值的相反数是为:﹣3,
故选:A.
2.(3分)截至2022年5月4日,我国31个省(自治区、直辖市)和新疆生产建设兵团累计报告接种新冠病毒疫苗约3350000000剂次,将3350000000用科学记数法表示为( )
A.335×107 B.33.5×108
C.3.35×109 D.0.335×1010
【解答】解:3350000000=3.35×109.
故选:C.
3.(3分)下列图形旋转一周,能得到如图几何体的是( )
A. B. C. D.
【解答】解:A、将图形绕直线旋转一周,能得到如图的几何体,故A符合题意;
B、将图形绕直线旋转一周,不能得到如图的几何体,故B不符合题意;
C、将图形绕直线旋转一周,不能得到如图的几何体,故C不符合题意;
D、将图形绕直线旋转一周,不能得到如图的几何体,故D不符合题意;
故选:A.
4.(3分)下列调查中,最适合采用全面调查(普查)的是( )
A.调查全国中小学生对第二次太空授课的满意度
B.调查全国人民,掌握新冠防疫知识情况
C.了解某类型医用口罩的质量
D.检查神舟飞船十三号的各零部件
【解答】解:A.调查全国中小学生对第二次太空授课的满意度,适合抽样调查,故本选项不符合题意;
B.调查全国人民,掌握新冠防疫知识情况,适合抽样调查,故本选项不符合题意;
C.了解某类型医用口罩的质量,适合抽样调查,故本选项不符合题意;
D.检查神舟飞船十三号的各零部件,事件重大,适合全面调查,故本选项符合题意.
故选:D.
5.(3分)下列可以表示37.48°的是( )
A.37°12′36″ B.37°12′38″ C.37°26′38″ D.37°28′48″
【解答】解:37.48°=37°28′48″,
故选:D.
6.(3分)代数式﹣0.3x,0,2m2n3﹣5m4,,,,﹣2a2b2c,中单项式有( )
A.5个 B.6个 C.7个 D.8个
【解答】解:∵2m2n3﹣5m4,是多项式,﹣0.3x,0,,,,﹣2a2b2c都是单项式,
∴单项式有6个,
故选:B.
7.(3分)以∠AOB的顶点O为端点引射线OC,使∠AOC:∠BOC=5:4,若∠AOB=27°,则∠AOC为( )
A.15或108° B.12或135°
C.15°或135° D.以上答案都不正确
【解答】解:由题知,OC的位置存在以下两种情况:
∴∠AOC=27°×=15°或∠AOC=27°×=135°,
故选:C.
8.(3分)某工程甲独做需8天完成,乙独做需10天完成.现在由甲先做3天,然后甲和乙合作共同完成.若设完成此项工程共需x天,则下列方程正确的是( )
A.+ B.+
C.+ D.+
【解答】解:依题意得:+.
故选:C.
9.(3分)观察下列一组图形,其中图形①中共有2颗星,图形②中共有6颗星,图形③中共有11颗星,图形④中共有17颗星,.按此规律,图形⑨中星星的颗数是( )
A.51 B.53 C.61 D.62
【解答】解:设图形n中星星的颗数是an(n为正整数),
∵a1=2=1+1,a2=6=(1+2)+3,a3=11=(1+2+3)+5,a4=17=(1+2+3+4)+7,
∴an=1+2+…+n+(2n﹣1)=+(2n﹣1)=+n﹣1,
∴a9=×92+×9﹣1=62.
故选:D.
10.(3分)a是不为2的有理数,我们把称为a的“哈利数”.如:3的“哈利数”是=﹣2,﹣2的“哈利数”是=,已知a1=5,a2是a1的“哈利数”,a3是a2的“哈利数”,a4是a3的“哈利数”,…,依此类推,则a2022等于( )
A. B.﹣ C. D.5
【解答】解:∵a1=5,
∴a2=,a3=,a4=,a5==5,……,
∴每四次运算结果循环出现,
∵2022÷4=505……2,
∴a2022=a2=﹣,
故选:B.
二、填空题
11.(3分)一架直升机从高度为500米的位置开始,先以20米/秒的速度垂直上升50秒,再以12米/秒的速度垂直下降100秒,这时飞机所在的高度是 300 米.
【解答】解:由题意可得:
500+20×50﹣12×100
=500+1000﹣1200
=300(米).
故这时飞机所在的高度是300米,
故答案为:300.
12.(3分)单项式与2y3x3的和仍是单项式,则(m+n)2023= ﹣1 .
【解答】解:∵单项式与2y3x3的和仍是单项式,
∴与2y3x3是同类项,
∴m+5=3,4﹣n=3,
解得m=﹣2,n=1,
∴(m+n)2023=﹣1,
故答案为:﹣1.
13.(3分)如图,已知C,D两点将线段AB分为三部分,且AC:CD:DB=2:3:4.若AB的中点为M,BD的中点为N,且MN=5cm,则AD= 10cm .
【解答】解:∵AC:CD:DB=2:3:4,
∴设AC=2x,CD=3x,DB=4x,
∴AB=9x,
∵AB的中点为M,BD的中点为N,
∴BM=AB=x,BN=BD=2x,
∵MN=5cm,
∴x﹣2x=5,
∴x=2,
∴AD=5x=10(cm),
故答案为:10cm.
14.(3分)若3m2+4m﹣6的值为9,则的值为 ﹣3 .
【解答】解:∵3m2+4m﹣6的值为9,
∴3m2+4m﹣6=9.
∴3m2+4m=15.
∴m2+m=5.
∴
=5﹣8
=﹣3.
故答案为:﹣3.
15.(3分)已知等式(m﹣3)x|m|﹣2+5=0是关于x的一元一次方程,则m3= ﹣27 .
【解答】解:根据题意,得|m|﹣2=1且m﹣3≠0,
解得m=﹣3,
∴m3=﹣27.
故答案为:﹣27.
16.(3分)有理数a,b,c,满足|a+b+c|=a+b﹣c,且c≠0,则|a+b﹣c+3|﹣|c﹣6|= ﹣3 .
【解答】解:当a+b+c≥0时,a+b+c=a+b﹣c,c≠0,不符合题意;
当a+b+c小于0时,﹣a﹣b=a+b,a+b=0,则c小于0,
∴|a+b﹣c+3|﹣|c﹣6|
=0+3﹣c﹣(6﹣c)
=﹣3,
故答案为:﹣3.
三、解答题
17.计算:
(1)(﹣3)×(﹣4)+(﹣2)3÷4;
(2);
(3)5(x+8)﹣5=6(4x﹣8);
(4).
【解答】解:(1)(﹣3)×(﹣4)+(﹣2)3÷4
=12﹣8÷4
=12﹣2
=10;
(2)
=×(﹣1)﹣6÷(﹣9)
=﹣
=;
(3)5(x+8)﹣5=6(4x﹣8)
5x+40﹣5=24x﹣48,
5x﹣24x=﹣48﹣40+5,
﹣19x=﹣83,
∴x=;
(4),
原方程可化为,
3(4x+21)﹣5(50﹣20x)=9,
12x+63﹣250+100x=9,
112x=9﹣63+250,
112x=196,
∴x=.
18.先化简,再求值:已知(a﹣1)2+|b+2|=0,求代数式(6a2﹣2ab)﹣2的值.
【解答】解:(6a2﹣2ab)﹣2
=6a2﹣2ab﹣6a2﹣8ab+b2
=﹣10ab+b2,
∵(a﹣1)2+|b+2|=0,
∴a﹣1=0,b+2=0,
解得:a=1,b=﹣2,
∴原式=﹣10×1×(﹣2)+
=20+
=20+1
=21.
19.为进一步加强学生“学党史、知党情、跟党走”的信心,培养学生的民族精神和爱国主义情怀,某学校组织开展以“观看红色电影,点燃红色初心”为主题的教育活动.电影票价格表如下:
购票张数 1至40 41至80 80以上
每张票的价格 20元 18元 免2张门票,其余每张17元
该校七年级两个班共有83名学生去看电影,其中七(1)班的学生人数超过30,但不足40.
(1)如果两个班都以班为单位单独购票,一共付了1572元.求七(2)班学生的人数;
(2)在(1)所得的班级学生人数下,如果七(1)班有7名学生因有比赛任务不能参加这次活动,请你为两个班级设计购买电影票的方案,并指出最省钱的方案.
【解答】解:(1)设七(1)班有x名学生,则七(2)班有(83﹣x)名学生,
根据题意得:20x+18(83﹣x)=1572,
解得:x=39,
∴83﹣x=83﹣39=44(人).
答:七(2)班有44名学生;
(2)方案1:以班为单位单独购票,所需费用为20×(39﹣7)+18×44=1432(元);
方案2:两个班联合购买正好张数的票,所需费用为18×(83﹣7)=1368(元);
方案3:两个班联合购买81张票,所需费用为17×(81﹣2)=1343(元).
∵1432>1368>1343,
∴最省钱的方案为两个班联合购买81张票.
20.某班学生列队从学校到一个农场去参加劳动,以每小时4千米的速度行进.走完1千米时,一个学生奉命回学校取一件东西,他以每小时5千米的速度跑回学校,取了东西后又立即以同样的速度跑步追赶队伍,结果在距农场1.5千米的地方追上队伍,求学校到农场的距离.
【解答】解:设学校到农场的路程为x千米,
依题意,得:=,
解得:x=10.5.
答:学校到农场的路程为10.5千米.
21.规定:若关于x的一元一次方程ax+b=0的解为x=a+b,则称该方程是“奇异方程”.例如:的解为,因为,所以该方程是“奇异方程”.
(1)若关于x的一元一次方程3x+m=0是“奇异方程”,则m的值为 .
(2)若关于x的一元一次方程2x+mn+m=0和﹣2x+mn+n=0都是“奇异方程”,则代数式18(mn+m)2﹣(mn+n)2的值为 16 .
【解答】解:(1)∵关于x的一元一次方程3x+m=0是“奇异方程”,
∴3+m=﹣,
解得m=,
故答案为:;
(2)∵关于x的一元一次方程2x+mn+m=0和﹣2x+mn+n=0都是“奇异方程”,
∴2+mn+m=﹣,﹣2+mn+n=,
∴mn+m=﹣,mn+n=4,
∴18(mn+m)2﹣(mn+n)2=18×(﹣)2﹣42=32﹣16=16,
故答案为:16.
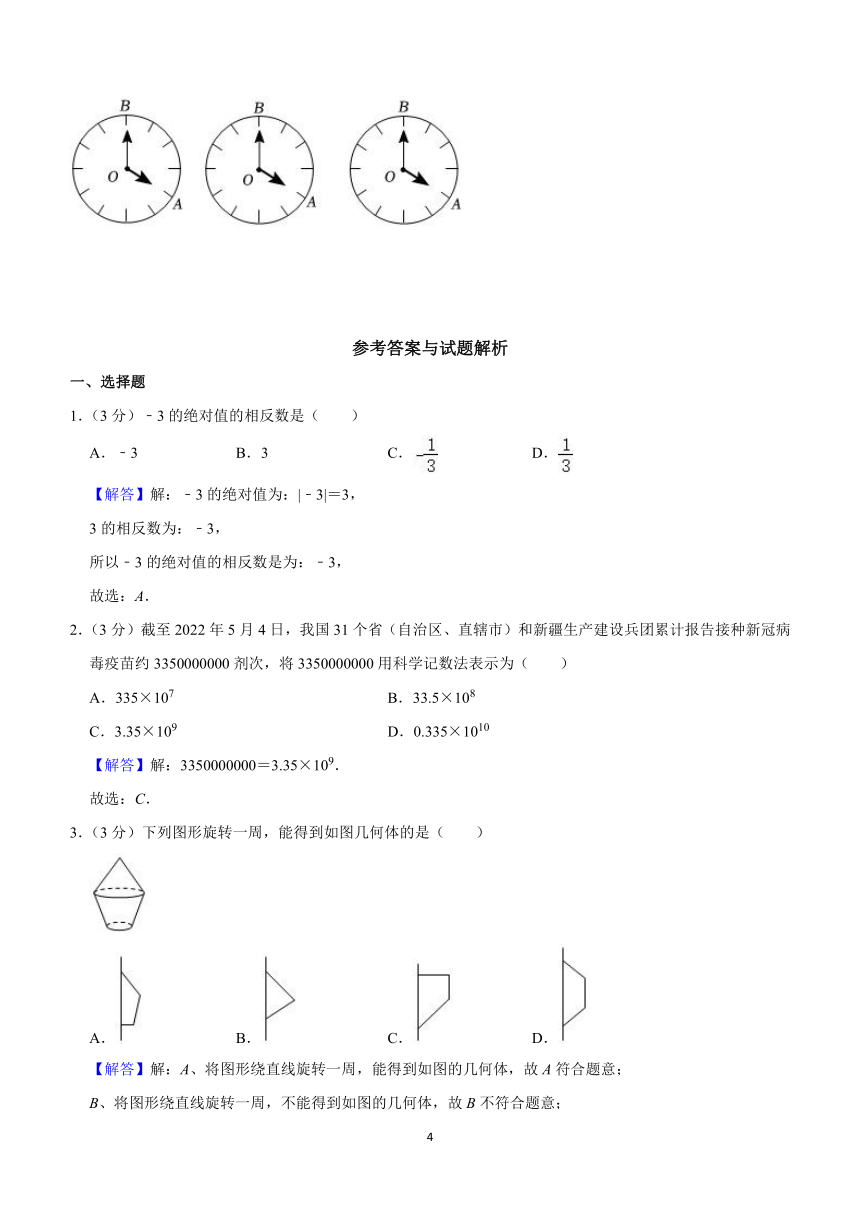
22.钟表是我们日常生活中常用的计时工具.在圆形钟面上,把一周等分成12个大格,每个大格等分成5个小格.如图,设在4:00时,分针的位置为OB,时针的位置为OA,运动后的分针为OP,时针为OQ(本题中的角均指小于180°的角).若在4:00至5:00之间,OM在∠AOP内,ON在∠AOQ内,,.
(1)当OP在∠AOB内时,求∠POM和∠AON之间的数量关系;
(2)从4:00开始几分钟后,∠MON=111°.(直接写答案)
【解答】解:(1)当OP在∠AOB内时,
设运动时间为t秒,
则0<t<,
∴∠BOP=(6t)°,∠AOQ=(0.5t)°,
∵∠POM=∠AOP,∠NOQ=∠AOQ,
∴∠POQ=∠AOB﹣∠BOP+∠AOQ=120°﹣(6t)°+(0.5t)°=120°﹣(5.5t)°,
∠POM=α,则∠AOP=3α,∠AOM=2α,
∴∠AOQ=∠POQ﹣∠AOP=120°﹣(5.5t)°﹣3α,
∠NOQ=∠AOQ=40°﹣()°﹣α,
∴∠AON=∠AOQ﹣∠NOQ=80°﹣()°﹣2α,
∵∠AOQ=(0.5t)°,
∴∠AON=(×)°=()°,
∴80°﹣()°﹣2α=()°,
∴α=40°﹣(2t)°,
即∠POM=40°﹣(2t)°,∠AON=()°,
∵()°×6+40°﹣(2t)°=40°,
∴6∠AON+∠POM=40°,
(2)设从4:00开始m分钟后,∠MON=111°,
当OP未追上OQ时,
∠MON=∠AOM+∠AON=(120°﹣∠BOP)+∠AOQ=(120°﹣∠BOP+∠AOQ)=80°﹣()°,
∴80°﹣()°=111°,
∴()°=﹣31°<0(舍去).
当OP超过OQ时,
∠MON=∠AOP﹣∠POM﹣∠AON=(6m)°﹣120°﹣[(6m)°﹣120°]﹣(0.5m)=()°﹣80°,
∴()°﹣80°=111°,
∴m=.
答:从4:00开始分钟后,∠MON=111°.
一、选择题
1.(3分)﹣3的绝对值的相反数是( )
A.﹣3 B.3 C. D.
2.(3分)截至2022年5月4日,我国31个省(自治区、直辖市)和新疆生产建设兵团累计报告接种新冠病毒疫苗约3350000000剂次,将3350000000用科学记数法表示为( )
A.335×107 B.33.5×108
C.3.35×109 D.0.335×1010
3.(3分)下列图形旋转一周,能得到如图几何体的是( )
A. B. C. D.
4.(3分)下列调查中,最适合采用全面调查(普查)的是( )
A.调查全国中小学生对第二次太空授课的满意度
B.调查全国人民,掌握新冠防疫知识情况
C.了解某类型医用口罩的质量
D.检查神舟飞船十三号的各零部件
5.(3分)下列可以表示37.48°的是( )
A.37°12′36″ B.37°12′38″ C.37°26′38″ D.37°28′48″
6.(3分)代数式﹣0.3x,0,2m2n3﹣5m4,,,,﹣2a2b2c,中单项式有( )
A.5个 B.6个 C.7个 D.8个
7.(3分)以∠AOB的顶点O为端点引射线OC,使∠AOC:∠BOC=5:4,若∠AOB=27°,则∠AOC为( )
A.15或108° B.12或135°
C.15°或135° D.以上答案都不正确
8.(3分)某工程甲独做需8天完成,乙独做需10天完成.现在由甲先做3天,然后甲和乙合作共同完成.若设完成此项工程共需x天,则下列方程正确的是( )
A.+ B.+
C.+ D.+
9.(3分)观察下列一组图形,其中图形①中共有2颗星,图形②中共有6颗星,图形③中共有11颗星,图形④中共有17颗星,.按此规律,图形⑨中星星的颗数是( )
A.51 B.53 C.61 D.62
10.(3分)a是不为2的有理数,我们把称为a的“哈利数”.如:3的“哈利数”是=﹣2,﹣2的“哈利数”是=,已知a1=5,a2是a1的“哈利数”,a3是a2的“哈利数”,a4是a3的“哈利数”,…,依此类推,则a2022等于( )
A. B.﹣ C. D.5
二、填空题
11.(3分)一架直升机从高度为500米的位置开始,先以20米/秒的速度垂直上升50秒,再以12米/秒的速度垂直下降100秒,这时飞机所在的高度是 米.
12.(3分)单项式与2y3x3的和仍是单项式,则(m+n)2023= .
13.(3分)如图,已知C,D两点将线段AB分为三部分,且AC:CD:DB=2:3:4.若AB的中点为M,BD的中点为N,且MN=5cm,则AD= .
14.(3分)若3m2+4m﹣6的值为9,则的值为 .
15.(3分)已知等式(m﹣3)x|m|﹣2+5=0是关于x的一元一次方程,则m3= .
16.(3分)有理数a,b,c,满足|a+b+c|=a+b﹣c,且c≠0,则|a+b﹣c+3|﹣|c﹣6|= .
三、解答题
17.计算:
(1)(﹣3)×(﹣4)+(﹣2)3÷4;
(2);
(3)5(x+8)﹣5=6(4x﹣8);
(4).
18.先化简,再求值:已知(a﹣1)2+|b+2|=0,求代数式(6a2﹣2ab)﹣2的值.
19.为进一步加强学生“学党史、知党情、跟党走”的信心,培养学生的民族精神和爱国主义情怀,某学校组织开展以“观看红色电影,点燃红色初心”为主题的教育活动.电影票价格表如下:
购票张数 1至40 41至80 80以上
每张票的价格 20元 18元 免2张门票,其余每张17元
该校七年级两个班共有83名学生去看电影,其中七(1)班的学生人数超过30,但不足40.
(1)如果两个班都以班为单位单独购票,一共付了1572元.求七(2)班学生的人数;
(2)在(1)所得的班级学生人数下,如果七(1)班有7名学生因有比赛任务不能参加这次活动,请你为两个班级设计购买电影票的方案,并指出最省钱的方案.
20.某班学生列队从学校到一个农场去参加劳动,以每小时4千米的速度行进.走完1千米时,一个学生奉命回学校取一件东西,他以每小时5千米的速度跑回学校,取了东西后又立即以同样的速度跑步追赶队伍,结果在距农场1.5千米的地方追上队伍,求学校到农场的距离.
21.规定:若关于x的一元一次方程ax+b=0的解为x=a+b,则称该方程是“奇异方程”.例如:的解为,因为,所以该方程是“奇异方程”.
(1)若关于x的一元一次方程3x+m=0是“奇异方程”,则m的值为 .
(2)若关于x的一元一次方程2x+mn+m=0和﹣2x+mn+n=0都是“奇异方程”,则代数式18(mn+m)2﹣(mn+n)2的值为 .
22.钟表是我们日常生活中常用的计时工具.在圆形钟面上,把一周等分成12个大格,每个大格等分成5个小格.如图,设在4:00时,分针的位置为OB,时针的位置为OA,运动后的分针为OP,时针为OQ(本题中的角均指小于180°的角).若在4:00至5:00之间,OM在∠AOP内,ON在∠AOQ内,,.
(1)当OP在∠AOB内时,求∠POM和∠AON之间的数量关系;
(2)从4:00开始几分钟后,∠MON=111°.(直接写答案)
参考答案与试题解析
一、选择题
1.(3分)﹣3的绝对值的相反数是( )
A.﹣3 B.3 C. D.
【解答】解:﹣3的绝对值为:|﹣3|=3,
3的相反数为:﹣3,
所以﹣3的绝对值的相反数是为:﹣3,
故选:A.
2.(3分)截至2022年5月4日,我国31个省(自治区、直辖市)和新疆生产建设兵团累计报告接种新冠病毒疫苗约3350000000剂次,将3350000000用科学记数法表示为( )
A.335×107 B.33.5×108
C.3.35×109 D.0.335×1010
【解答】解:3350000000=3.35×109.
故选:C.
3.(3分)下列图形旋转一周,能得到如图几何体的是( )
A. B. C. D.
【解答】解:A、将图形绕直线旋转一周,能得到如图的几何体,故A符合题意;
B、将图形绕直线旋转一周,不能得到如图的几何体,故B不符合题意;
C、将图形绕直线旋转一周,不能得到如图的几何体,故C不符合题意;
D、将图形绕直线旋转一周,不能得到如图的几何体,故D不符合题意;
故选:A.
4.(3分)下列调查中,最适合采用全面调查(普查)的是( )
A.调查全国中小学生对第二次太空授课的满意度
B.调查全国人民,掌握新冠防疫知识情况
C.了解某类型医用口罩的质量
D.检查神舟飞船十三号的各零部件
【解答】解:A.调查全国中小学生对第二次太空授课的满意度,适合抽样调查,故本选项不符合题意;
B.调查全国人民,掌握新冠防疫知识情况,适合抽样调查,故本选项不符合题意;
C.了解某类型医用口罩的质量,适合抽样调查,故本选项不符合题意;
D.检查神舟飞船十三号的各零部件,事件重大,适合全面调查,故本选项符合题意.
故选:D.
5.(3分)下列可以表示37.48°的是( )
A.37°12′36″ B.37°12′38″ C.37°26′38″ D.37°28′48″
【解答】解:37.48°=37°28′48″,
故选:D.
6.(3分)代数式﹣0.3x,0,2m2n3﹣5m4,,,,﹣2a2b2c,中单项式有( )
A.5个 B.6个 C.7个 D.8个
【解答】解:∵2m2n3﹣5m4,是多项式,﹣0.3x,0,,,,﹣2a2b2c都是单项式,
∴单项式有6个,
故选:B.
7.(3分)以∠AOB的顶点O为端点引射线OC,使∠AOC:∠BOC=5:4,若∠AOB=27°,则∠AOC为( )
A.15或108° B.12或135°
C.15°或135° D.以上答案都不正确
【解答】解:由题知,OC的位置存在以下两种情况:
∴∠AOC=27°×=15°或∠AOC=27°×=135°,
故选:C.
8.(3分)某工程甲独做需8天完成,乙独做需10天完成.现在由甲先做3天,然后甲和乙合作共同完成.若设完成此项工程共需x天,则下列方程正确的是( )
A.+ B.+
C.+ D.+
【解答】解:依题意得:+.
故选:C.
9.(3分)观察下列一组图形,其中图形①中共有2颗星,图形②中共有6颗星,图形③中共有11颗星,图形④中共有17颗星,.按此规律,图形⑨中星星的颗数是( )
A.51 B.53 C.61 D.62
【解答】解:设图形n中星星的颗数是an(n为正整数),
∵a1=2=1+1,a2=6=(1+2)+3,a3=11=(1+2+3)+5,a4=17=(1+2+3+4)+7,
∴an=1+2+…+n+(2n﹣1)=+(2n﹣1)=+n﹣1,
∴a9=×92+×9﹣1=62.
故选:D.
10.(3分)a是不为2的有理数,我们把称为a的“哈利数”.如:3的“哈利数”是=﹣2,﹣2的“哈利数”是=,已知a1=5,a2是a1的“哈利数”,a3是a2的“哈利数”,a4是a3的“哈利数”,…,依此类推,则a2022等于( )
A. B.﹣ C. D.5
【解答】解:∵a1=5,
∴a2=,a3=,a4=,a5==5,……,
∴每四次运算结果循环出现,
∵2022÷4=505……2,
∴a2022=a2=﹣,
故选:B.
二、填空题
11.(3分)一架直升机从高度为500米的位置开始,先以20米/秒的速度垂直上升50秒,再以12米/秒的速度垂直下降100秒,这时飞机所在的高度是 300 米.
【解答】解:由题意可得:
500+20×50﹣12×100
=500+1000﹣1200
=300(米).
故这时飞机所在的高度是300米,
故答案为:300.
12.(3分)单项式与2y3x3的和仍是单项式,则(m+n)2023= ﹣1 .
【解答】解:∵单项式与2y3x3的和仍是单项式,
∴与2y3x3是同类项,
∴m+5=3,4﹣n=3,
解得m=﹣2,n=1,
∴(m+n)2023=﹣1,
故答案为:﹣1.
13.(3分)如图,已知C,D两点将线段AB分为三部分,且AC:CD:DB=2:3:4.若AB的中点为M,BD的中点为N,且MN=5cm,则AD= 10cm .
【解答】解:∵AC:CD:DB=2:3:4,
∴设AC=2x,CD=3x,DB=4x,
∴AB=9x,
∵AB的中点为M,BD的中点为N,
∴BM=AB=x,BN=BD=2x,
∵MN=5cm,
∴x﹣2x=5,
∴x=2,
∴AD=5x=10(cm),
故答案为:10cm.
14.(3分)若3m2+4m﹣6的值为9,则的值为 ﹣3 .
【解答】解:∵3m2+4m﹣6的值为9,
∴3m2+4m﹣6=9.
∴3m2+4m=15.
∴m2+m=5.
∴
=5﹣8
=﹣3.
故答案为:﹣3.
15.(3分)已知等式(m﹣3)x|m|﹣2+5=0是关于x的一元一次方程,则m3= ﹣27 .
【解答】解:根据题意,得|m|﹣2=1且m﹣3≠0,
解得m=﹣3,
∴m3=﹣27.
故答案为:﹣27.
16.(3分)有理数a,b,c,满足|a+b+c|=a+b﹣c,且c≠0,则|a+b﹣c+3|﹣|c﹣6|= ﹣3 .
【解答】解:当a+b+c≥0时,a+b+c=a+b﹣c,c≠0,不符合题意;
当a+b+c小于0时,﹣a﹣b=a+b,a+b=0,则c小于0,
∴|a+b﹣c+3|﹣|c﹣6|
=0+3﹣c﹣(6﹣c)
=﹣3,
故答案为:﹣3.
三、解答题
17.计算:
(1)(﹣3)×(﹣4)+(﹣2)3÷4;
(2);
(3)5(x+8)﹣5=6(4x﹣8);
(4).
【解答】解:(1)(﹣3)×(﹣4)+(﹣2)3÷4
=12﹣8÷4
=12﹣2
=10;
(2)
=×(﹣1)﹣6÷(﹣9)
=﹣
=;
(3)5(x+8)﹣5=6(4x﹣8)
5x+40﹣5=24x﹣48,
5x﹣24x=﹣48﹣40+5,
﹣19x=﹣83,
∴x=;
(4),
原方程可化为,
3(4x+21)﹣5(50﹣20x)=9,
12x+63﹣250+100x=9,
112x=9﹣63+250,
112x=196,
∴x=.
18.先化简,再求值:已知(a﹣1)2+|b+2|=0,求代数式(6a2﹣2ab)﹣2的值.
【解答】解:(6a2﹣2ab)﹣2
=6a2﹣2ab﹣6a2﹣8ab+b2
=﹣10ab+b2,
∵(a﹣1)2+|b+2|=0,
∴a﹣1=0,b+2=0,
解得:a=1,b=﹣2,
∴原式=﹣10×1×(﹣2)+
=20+
=20+1
=21.
19.为进一步加强学生“学党史、知党情、跟党走”的信心,培养学生的民族精神和爱国主义情怀,某学校组织开展以“观看红色电影,点燃红色初心”为主题的教育活动.电影票价格表如下:
购票张数 1至40 41至80 80以上
每张票的价格 20元 18元 免2张门票,其余每张17元
该校七年级两个班共有83名学生去看电影,其中七(1)班的学生人数超过30,但不足40.
(1)如果两个班都以班为单位单独购票,一共付了1572元.求七(2)班学生的人数;
(2)在(1)所得的班级学生人数下,如果七(1)班有7名学生因有比赛任务不能参加这次活动,请你为两个班级设计购买电影票的方案,并指出最省钱的方案.
【解答】解:(1)设七(1)班有x名学生,则七(2)班有(83﹣x)名学生,
根据题意得:20x+18(83﹣x)=1572,
解得:x=39,
∴83﹣x=83﹣39=44(人).
答:七(2)班有44名学生;
(2)方案1:以班为单位单独购票,所需费用为20×(39﹣7)+18×44=1432(元);
方案2:两个班联合购买正好张数的票,所需费用为18×(83﹣7)=1368(元);
方案3:两个班联合购买81张票,所需费用为17×(81﹣2)=1343(元).
∵1432>1368>1343,
∴最省钱的方案为两个班联合购买81张票.
20.某班学生列队从学校到一个农场去参加劳动,以每小时4千米的速度行进.走完1千米时,一个学生奉命回学校取一件东西,他以每小时5千米的速度跑回学校,取了东西后又立即以同样的速度跑步追赶队伍,结果在距农场1.5千米的地方追上队伍,求学校到农场的距离.
【解答】解:设学校到农场的路程为x千米,
依题意,得:=,
解得:x=10.5.
答:学校到农场的路程为10.5千米.
21.规定:若关于x的一元一次方程ax+b=0的解为x=a+b,则称该方程是“奇异方程”.例如:的解为,因为,所以该方程是“奇异方程”.
(1)若关于x的一元一次方程3x+m=0是“奇异方程”,则m的值为 .
(2)若关于x的一元一次方程2x+mn+m=0和﹣2x+mn+n=0都是“奇异方程”,则代数式18(mn+m)2﹣(mn+n)2的值为 16 .
【解答】解:(1)∵关于x的一元一次方程3x+m=0是“奇异方程”,
∴3+m=﹣,
解得m=,
故答案为:;
(2)∵关于x的一元一次方程2x+mn+m=0和﹣2x+mn+n=0都是“奇异方程”,
∴2+mn+m=﹣,﹣2+mn+n=,
∴mn+m=﹣,mn+n=4,
∴18(mn+m)2﹣(mn+n)2=18×(﹣)2﹣42=32﹣16=16,
故答案为:16.
22.钟表是我们日常生活中常用的计时工具.在圆形钟面上,把一周等分成12个大格,每个大格等分成5个小格.如图,设在4:00时,分针的位置为OB,时针的位置为OA,运动后的分针为OP,时针为OQ(本题中的角均指小于180°的角).若在4:00至5:00之间,OM在∠AOP内,ON在∠AOQ内,,.
(1)当OP在∠AOB内时,求∠POM和∠AON之间的数量关系;
(2)从4:00开始几分钟后,∠MON=111°.(直接写答案)
【解答】解:(1)当OP在∠AOB内时,
设运动时间为t秒,
则0<t<,
∴∠BOP=(6t)°,∠AOQ=(0.5t)°,
∵∠POM=∠AOP,∠NOQ=∠AOQ,
∴∠POQ=∠AOB﹣∠BOP+∠AOQ=120°﹣(6t)°+(0.5t)°=120°﹣(5.5t)°,
∠POM=α,则∠AOP=3α,∠AOM=2α,
∴∠AOQ=∠POQ﹣∠AOP=120°﹣(5.5t)°﹣3α,
∠NOQ=∠AOQ=40°﹣()°﹣α,
∴∠AON=∠AOQ﹣∠NOQ=80°﹣()°﹣2α,
∵∠AOQ=(0.5t)°,
∴∠AON=(×)°=()°,
∴80°﹣()°﹣2α=()°,
∴α=40°﹣(2t)°,
即∠POM=40°﹣(2t)°,∠AON=()°,
∵()°×6+40°﹣(2t)°=40°,
∴6∠AON+∠POM=40°,
(2)设从4:00开始m分钟后,∠MON=111°,
当OP未追上OQ时,
∠MON=∠AOM+∠AON=(120°﹣∠BOP)+∠AOQ=(120°﹣∠BOP+∠AOQ)=80°﹣()°,
∴80°﹣()°=111°,
∴()°=﹣31°<0(舍去).
当OP超过OQ时,
∠MON=∠AOP﹣∠POM﹣∠AON=(6m)°﹣120°﹣[(6m)°﹣120°]﹣(0.5m)=()°﹣80°,
∴()°﹣80°=111°,
∴m=.
答:从4:00开始分钟后,∠MON=111°.
同课章节目录
