2023-2024学年七年级下册人教版数学5.1 相交线 同步练习(含解析)
文档属性
| 名称 | 2023-2024学年七年级下册人教版数学5.1 相交线 同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 245.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-10 00:00:00 | ||
图片预览


文档简介
5.1 相交线 同步练习
一、单选题(共10小题)
1. 如图所示, 和 是对顶角的图形有
A. 个 B. 个 C. 个 D. 个
2. 如图, 和 是同位角的是
A. B. C. D.
3. 如图, 是锐角三角形,过点 作 ,垂足为 ,则点 到直线 的距离是
A. 线段 的长 B. 线段 的长 C. 线段 的长 D. 线段 的长
4. 如图,直线 , 被直线 所截,则 的同旁内角是
A. B. C. D.
5. 下列图形中, 与 是同位角的有
A. ②③④ B. ①②④ C. ②③ D. ③④
6. 如图,下列说法中错误的是
A. 和 是同位角 B. 和 是同位角
C. 和 是内错角 D. 和 是同旁内角
7. 如图,三条直线 ,, 相交于点 ,则 等于
A. B. C. D.
8. 下列画图语句中,不能画图的是
A. 过点 画 ,点 是垂足
B. 画直线 ,使它平分线段
C. 过点 画线段 的垂直平分线
D. 画线段 的中垂线
9. 如图, 的同旁内角有
A. 个 B. 个 C. 个 D. 个
10. 中国滑雪天才少女谷爱凌在 年北京冬奥会的赛场上斩获“自由式滑雪大跳台”首金,这是她获得的首个冬奥会奖牌,也是中国运动员第一次参加冬奥会大跳台的比赛.项目图标如图;则在下列判断中① 与 是对顶角;② 与 是同旁内角;③ 与 是同旁内角;④ 与 是内错角,其中正确的有 个.
A. B. C. D.
二、填空题(共6小题)
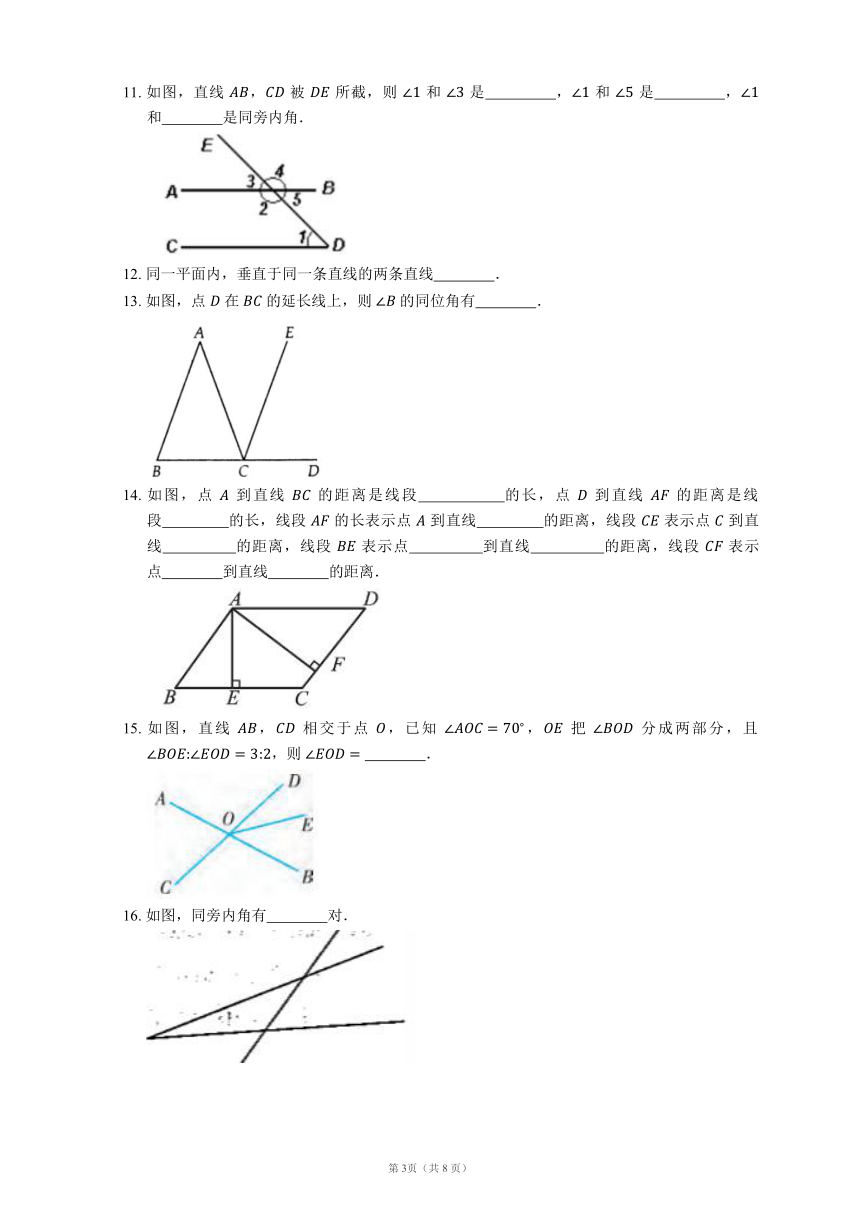
11. 如图,直线 , 被 所截,则 和 是 , 和 是 , 和 是同旁内角.
12. 同一平面内,垂直于同一条直线的两条直线 .
13. 如图,点 在 的延长线上,则 的同位角有 .
14. 如图,点 到直线 的距离是线段 的长,点 到直线 的距离是线段 的长,线段 的长表示点 到直线 的距离,线段 表示点 到直线 的距离,线段 表示点 到直线 的距离,线段 表示点 到直线 的距离.
15. 如图,直线 , 相交于点 ,已知 , 把 分成两部分,且 ,则 .
16. 如图,同旁内角有 对.
三、解答题(共4小题;共8分)
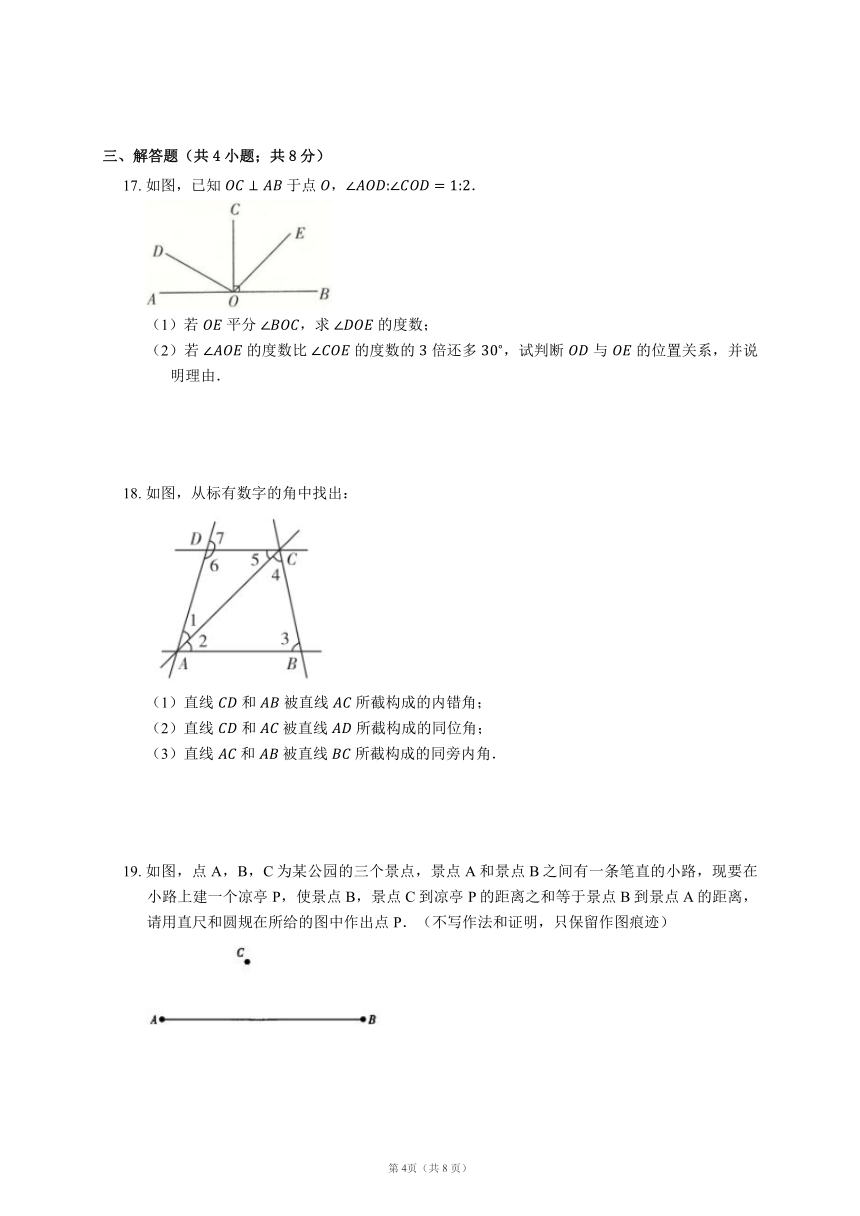
17. 如图,已知 于点 ,.
(1)若 平分 ,求 的度数;
(2)若 的度数比 的度数的 倍还多 ,试判断 与 的位置关系,并说明理由.
18. 如图,从标有数字的角中找出:
(1)直线 和 被直线 所截构成的内错角;
(2)直线 和 被直线 所截构成的同位角;
(3)直线 和 被直线 所截构成的同旁内角.
19. 如图,点A,B,C为某公园的三个景点,景点A和景点B之间有一条笔直的小路,现要在小路上建一个凉亭P,使景点B,景点C到凉亭P的距离之和等于景点B到景点A的距离,请用直尺和圆规在所给的图中作出点P.(不写作法和证明,只保留作图痕迹)
20. 如图,已知 为直线 上的一点, 于点 , 于点 , 平分 ,点 在 的反向延长线上.
(1)当 在 内, 在 内时,如图 所示,直接写出 和 之间的数量关系;
(2)当 在 内且 在 内时,如图 所示,试问()中 和 之间的数量关系是否发生变化 并说明理由.
答案
一 单选题
1. A
2. C
3. B
4. B
5. B
6. A
7. B
8. C
9. B
【解析】由图知:
和 在截线 的同侧,且都在被截直线 , 的内侧;
和 是同旁内角.
和 在截线 的同侧,且都在被截直线 , 的内侧;
和 是同旁内角.
和 在截线 的同侧,且都在被截直线 , 的内侧;
和 是同旁内角.
故答案为 ,,.
故选:B.
10. C
【解析】①.根据对顶角的定义(角的两边互为反向延长线的两个角互为对顶角), 与 是对顶角,那么①正确.
②.根据同旁内角的定义(两条直线被第三条直线所截,在被截线之间并且在截线同一侧的两个角是同旁内角), 与 是同旁内角,那么②正确.
③.根据同旁内角的定义以及邻补角的定义, 与 不是同旁内角,而是邻补角,那么③错误.
④.根据内错角的定义(两条直线被第三条直线所截,在被截线之间并且在截线两侧的两个角是内错角), 与 是内错角,那么④正确.
综上:正确的有①②④,共 个.
故选:C.
二 填空题
11. 略,略,略
12. 略
13. ,
14. 略,略,略,略,略,略,略,略
15.
16.
三 解答题
17. (1) 因为 于点 ,
所以 .
因为 ,
所以 .
因为 平分 ,,
所以 ,
所以 ,
即 .
(2) .理由如下:
因为 于点 ,
所以 .
因为 ,
所以 .
由题意得 ,
又因为 ,
所以 ,
所以 .
因为 ,
所以 .
18. (1) 直线 和 被直线 所截构成的内错角是 和 .
(2) 直线 和 被直线 所截构成的同位角是 和 .
(3) 直线 和 被直线 所截构成的同旁内角是 和 .
19. 如答图所示.
20. (1) .
(2) .
【解析】(1)利用垂直的定义,CD⊥AB,PO⊥EO,等量代换得∠COP=∠BOE,利用角平分线的性质,得∠POM=∠POB=(90°-∠POC),∠COF=90°-∠COP,得出结论;
(2)利用垂直的定义,同角的余角相等可得∠COP=∠AOF,可推出∠COP+∠COB=∠AOF+∠AOC,即∠BOP=∠COF,由对顶角相等得∠AOF=∠BOE=∠COP,利用角平分线的性质,得∠COP+∠COM=∠BOE+∠MOE,即∠POM=∠BOP,等量代换得出结论.
解:(1)∠POM=∠COF.
证明:∵CD⊥AB,
∴∠COP+∠BOP=90°,
∵OP⊥OE,
∴∠BOE+∠BOP=90°,
∴∠COP=∠BOE,
∵OM平分∠COE,
∴∠POM=∠MOB=∠POB= (90° ∠POC),
∵∠COF=90° ∠COP,
∴∠POM=∠COF;
(2)不发生变化.理由:∵CD⊥AB于点O,
∴∠AOP+∠COP=90°.
∵PO⊥OE于点O,
∴∠AOP+∠AOF=90°,
∴∠COP=∠AOF.
又∵∠AOC=∠COB=90°,
∴∠COP+∠COB=∠AOF+∠AOC,
即∠BOP=∠COF.
∵∠AOF=∠BOE,∴∠COP=∠BOE.
∵OM平分∠COE,∴∠COM=∠MOE,
∴∠COP+∠COM=∠BOE+∠MOE,
∴∠POM=∠BOP,
∴∠POM=∠COF.
故答案为:(1)∠POM=∠COF,理由见解析;(2)∠POM=∠COF,理由见解析.
第1页(共8 页)
一、单选题(共10小题)
1. 如图所示, 和 是对顶角的图形有
A. 个 B. 个 C. 个 D. 个
2. 如图, 和 是同位角的是
A. B. C. D.
3. 如图, 是锐角三角形,过点 作 ,垂足为 ,则点 到直线 的距离是
A. 线段 的长 B. 线段 的长 C. 线段 的长 D. 线段 的长
4. 如图,直线 , 被直线 所截,则 的同旁内角是
A. B. C. D.
5. 下列图形中, 与 是同位角的有
A. ②③④ B. ①②④ C. ②③ D. ③④
6. 如图,下列说法中错误的是
A. 和 是同位角 B. 和 是同位角
C. 和 是内错角 D. 和 是同旁内角
7. 如图,三条直线 ,, 相交于点 ,则 等于
A. B. C. D.
8. 下列画图语句中,不能画图的是
A. 过点 画 ,点 是垂足
B. 画直线 ,使它平分线段
C. 过点 画线段 的垂直平分线
D. 画线段 的中垂线
9. 如图, 的同旁内角有
A. 个 B. 个 C. 个 D. 个
10. 中国滑雪天才少女谷爱凌在 年北京冬奥会的赛场上斩获“自由式滑雪大跳台”首金,这是她获得的首个冬奥会奖牌,也是中国运动员第一次参加冬奥会大跳台的比赛.项目图标如图;则在下列判断中① 与 是对顶角;② 与 是同旁内角;③ 与 是同旁内角;④ 与 是内错角,其中正确的有 个.
A. B. C. D.
二、填空题(共6小题)
11. 如图,直线 , 被 所截,则 和 是 , 和 是 , 和 是同旁内角.
12. 同一平面内,垂直于同一条直线的两条直线 .
13. 如图,点 在 的延长线上,则 的同位角有 .
14. 如图,点 到直线 的距离是线段 的长,点 到直线 的距离是线段 的长,线段 的长表示点 到直线 的距离,线段 表示点 到直线 的距离,线段 表示点 到直线 的距离,线段 表示点 到直线 的距离.
15. 如图,直线 , 相交于点 ,已知 , 把 分成两部分,且 ,则 .
16. 如图,同旁内角有 对.
三、解答题(共4小题;共8分)
17. 如图,已知 于点 ,.
(1)若 平分 ,求 的度数;
(2)若 的度数比 的度数的 倍还多 ,试判断 与 的位置关系,并说明理由.
18. 如图,从标有数字的角中找出:
(1)直线 和 被直线 所截构成的内错角;
(2)直线 和 被直线 所截构成的同位角;
(3)直线 和 被直线 所截构成的同旁内角.
19. 如图,点A,B,C为某公园的三个景点,景点A和景点B之间有一条笔直的小路,现要在小路上建一个凉亭P,使景点B,景点C到凉亭P的距离之和等于景点B到景点A的距离,请用直尺和圆规在所给的图中作出点P.(不写作法和证明,只保留作图痕迹)
20. 如图,已知 为直线 上的一点, 于点 , 于点 , 平分 ,点 在 的反向延长线上.
(1)当 在 内, 在 内时,如图 所示,直接写出 和 之间的数量关系;
(2)当 在 内且 在 内时,如图 所示,试问()中 和 之间的数量关系是否发生变化 并说明理由.
答案
一 单选题
1. A
2. C
3. B
4. B
5. B
6. A
7. B
8. C
9. B
【解析】由图知:
和 在截线 的同侧,且都在被截直线 , 的内侧;
和 是同旁内角.
和 在截线 的同侧,且都在被截直线 , 的内侧;
和 是同旁内角.
和 在截线 的同侧,且都在被截直线 , 的内侧;
和 是同旁内角.
故答案为 ,,.
故选:B.
10. C
【解析】①.根据对顶角的定义(角的两边互为反向延长线的两个角互为对顶角), 与 是对顶角,那么①正确.
②.根据同旁内角的定义(两条直线被第三条直线所截,在被截线之间并且在截线同一侧的两个角是同旁内角), 与 是同旁内角,那么②正确.
③.根据同旁内角的定义以及邻补角的定义, 与 不是同旁内角,而是邻补角,那么③错误.
④.根据内错角的定义(两条直线被第三条直线所截,在被截线之间并且在截线两侧的两个角是内错角), 与 是内错角,那么④正确.
综上:正确的有①②④,共 个.
故选:C.
二 填空题
11. 略,略,略
12. 略
13. ,
14. 略,略,略,略,略,略,略,略
15.
16.
三 解答题
17. (1) 因为 于点 ,
所以 .
因为 ,
所以 .
因为 平分 ,,
所以 ,
所以 ,
即 .
(2) .理由如下:
因为 于点 ,
所以 .
因为 ,
所以 .
由题意得 ,
又因为 ,
所以 ,
所以 .
因为 ,
所以 .
18. (1) 直线 和 被直线 所截构成的内错角是 和 .
(2) 直线 和 被直线 所截构成的同位角是 和 .
(3) 直线 和 被直线 所截构成的同旁内角是 和 .
19. 如答图所示.
20. (1) .
(2) .
【解析】(1)利用垂直的定义,CD⊥AB,PO⊥EO,等量代换得∠COP=∠BOE,利用角平分线的性质,得∠POM=∠POB=(90°-∠POC),∠COF=90°-∠COP,得出结论;
(2)利用垂直的定义,同角的余角相等可得∠COP=∠AOF,可推出∠COP+∠COB=∠AOF+∠AOC,即∠BOP=∠COF,由对顶角相等得∠AOF=∠BOE=∠COP,利用角平分线的性质,得∠COP+∠COM=∠BOE+∠MOE,即∠POM=∠BOP,等量代换得出结论.
解:(1)∠POM=∠COF.
证明:∵CD⊥AB,
∴∠COP+∠BOP=90°,
∵OP⊥OE,
∴∠BOE+∠BOP=90°,
∴∠COP=∠BOE,
∵OM平分∠COE,
∴∠POM=∠MOB=∠POB= (90° ∠POC),
∵∠COF=90° ∠COP,
∴∠POM=∠COF;
(2)不发生变化.理由:∵CD⊥AB于点O,
∴∠AOP+∠COP=90°.
∵PO⊥OE于点O,
∴∠AOP+∠AOF=90°,
∴∠COP=∠AOF.
又∵∠AOC=∠COB=90°,
∴∠COP+∠COB=∠AOF+∠AOC,
即∠BOP=∠COF.
∵∠AOF=∠BOE,∴∠COP=∠BOE.
∵OM平分∠COE,∴∠COM=∠MOE,
∴∠COP+∠COM=∠BOE+∠MOE,
∴∠POM=∠BOP,
∴∠POM=∠COF.
故答案为:(1)∠POM=∠COF,理由见解析;(2)∠POM=∠COF,理由见解析.
第1页(共8 页)
