第三单元:长方体和正方体(单元复习课件)人教版五年级数学下册(共42张PPT)
文档属性
| 名称 | 第三单元:长方体和正方体(单元复习课件)人教版五年级数学下册(共42张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-10 00:00:00 | ||
图片预览






文档简介
(共42张PPT)
长方体和正方体
复习专题
人教版五年级数学下册
1
长方体和正方体的认识
2
长方体和正方体的表面积
3
长方体和正方体的体积
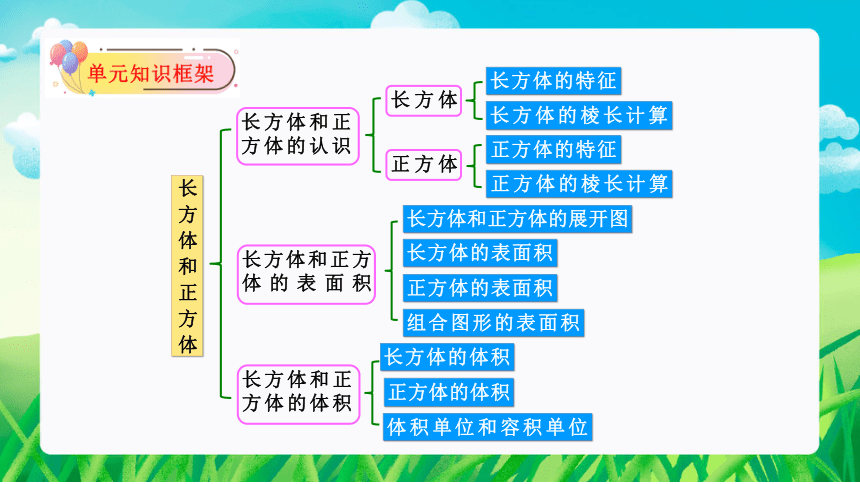
长方体和正方体
长方体和正方体的认识
长方体的特征
长方体的棱长计算
正方体的特征
长方体和正方体的表面积
长方体和正方体的展开图
长方体的表面积
正方体的表面积
长方体和正方体的体积
长方体的体积
正方体的体积
体积单位和容积单位
长方体
正方体
正方体的棱长计算
组合图形的表面积
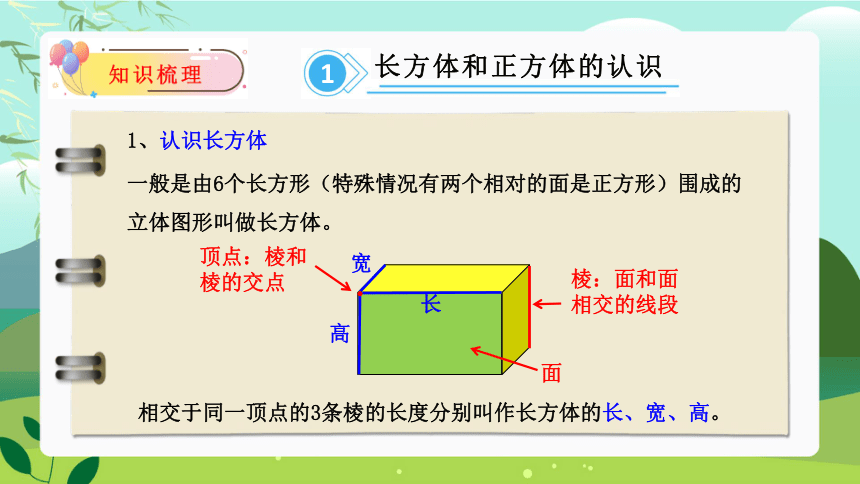
1、认识长方体
一般是由6个长方形(特殊情况有两个相对的面是正方形)围成的立体图形叫做长方体。
相交于同一顶点的3条棱的长度分别叫作长方体的长、宽、高。
1
长方体和正方体的认识
面
棱:面和面相交的线段
顶点:棱和棱的交点
长
高
宽
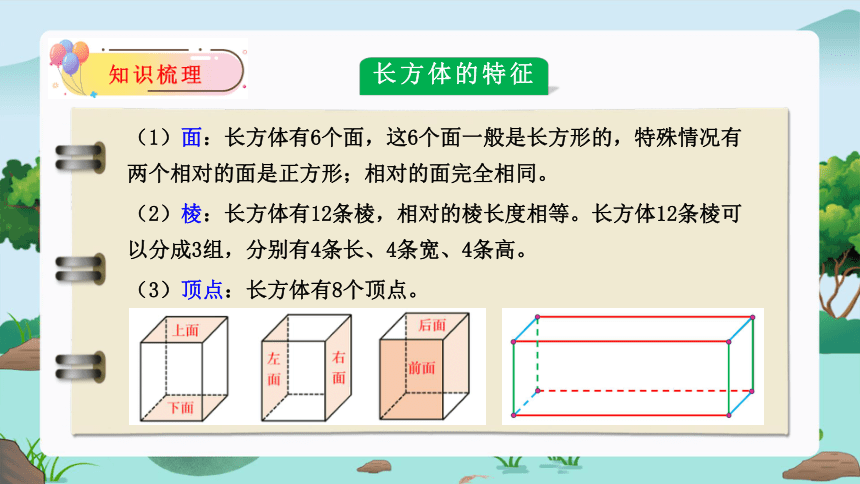
长方体的特征
(1)面:长方体有6个面,这6个面一般是长方形的,特殊情况有两个相对的面是正方形;相对的面完全相同。
(2)棱:长方体有12条棱,相对的棱长度相等。长方体12条棱可以分成3组,分别有4条长、4条宽、4条高。
(3)顶点:长方体有8个顶点。
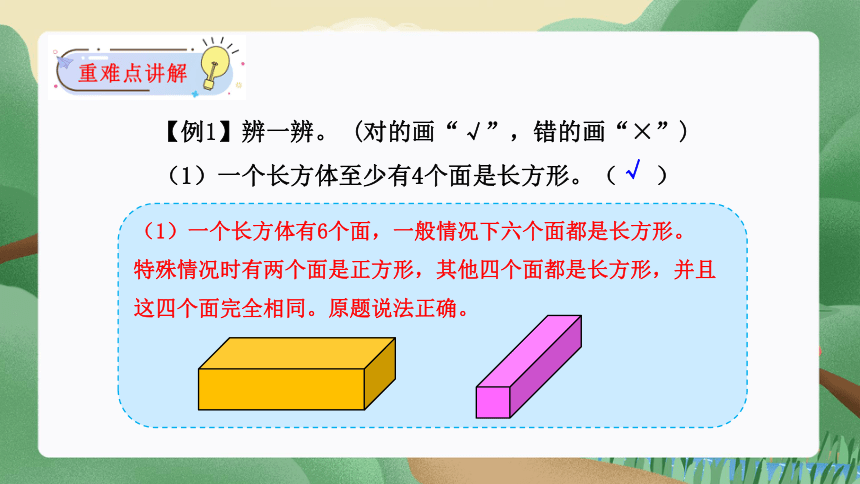
【例1】辨一辨。 (对的画“√”,错的画“×”)
(1)一个长方体至少有4个面是长方形。( )
(1)一个长方体有6个面,一般情况下六个面都是长方形。
特殊情况时有两个面是正方形,其他四个面都是长方形,并且这四个面完全相同。原题说法正确。
√
【例1】辨一辨。 (对的画“√”,错的画“×”)
(2)把一个长方体截成两个小长方体后,截面不可能是正方形。( )
(2)如果一个长方体有两个面是正方形,其他四个面都是长方形。这样的长方体截成两个小长方体,截面就是正方形,所以原题说法错误。
×
【例1】辨一辨。 (对的画“√”,错的画“×”)
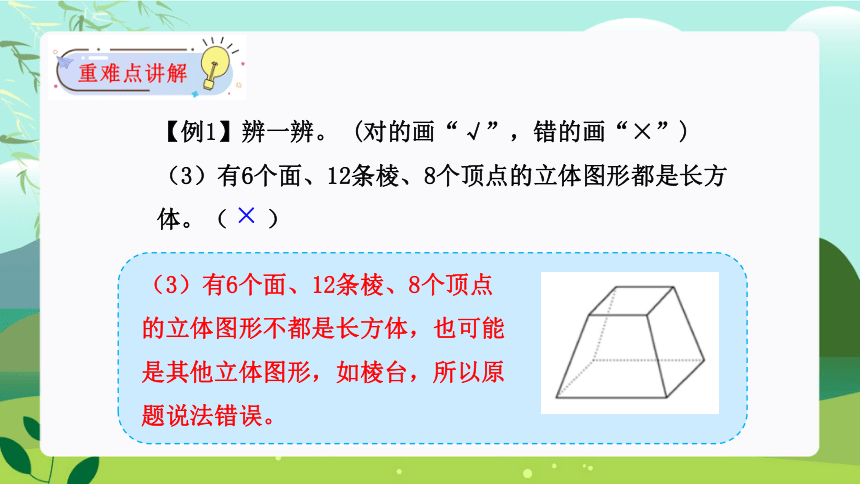
(3)有6个面、12条棱、8个顶点的立体图形都是长方体。( )
(3)有6个面、12条棱、8个顶点的立体图形不都是长方体,也可能是其他立体图形,如棱台,所以原题说法错误。
×
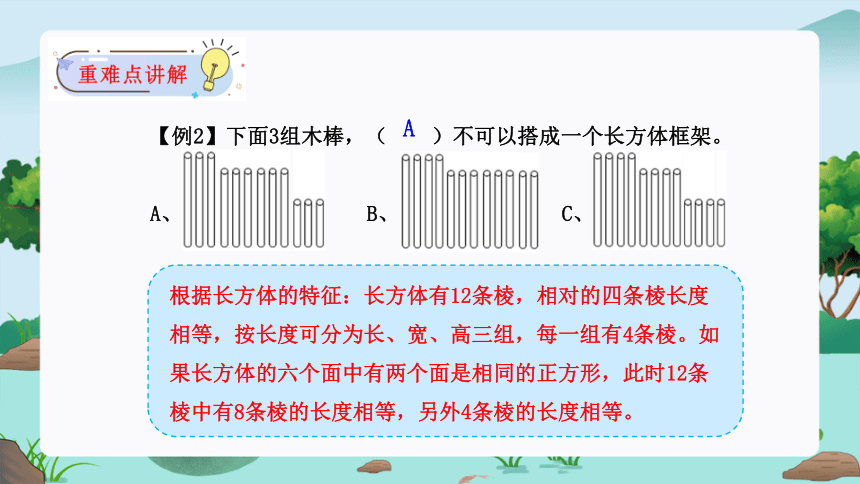
根据长方体的特征:长方体有12条棱,相对的四条棱长度相等,按长度可分为长、宽、高三组,每一组有4条棱。如果长方体的六个面中有两个面是相同的正方形,此时12条棱中有8条棱的长度相等,另外4条棱的长度相等。
A
【例2】下面3组木棒,( )不可以搭成一个长方体框架。
A、 B、 C、
长方体的棱长计算
长方体的棱长总和=(长+宽+高)×4
=长×4+宽×4+高×4
长=棱长总和÷4-宽-高
宽=棱长总和÷4-长-高
高=棱长总和÷4-长-宽
【例3】乾乾用小木棒制作了一个长方体花灯框架,这个长方体同一顶点上的三根木棒长度分别为25cm、18cm和12cm,则一共用了( )cm的木棒。
长方体的棱长总和=(长+宽+高)×4
(25+18+12)×4
=55×4
=220(cm)
220
【例4】给一个长1.8米,宽0.6米的玻璃柜台各边安上角铁,一共用去了15.2米的角铁,那么这个玻璃柜台的高是多少米?
高=棱长总和÷4-长-宽
15.2÷4-1.8-0.6
=3.8-1.8-0.6
=1.4(米)
答:这个玻璃柜台的高是1.4米。
认识正方体
1、认识正方体
由6个完全相同的正方形围成的立体图形叫做正方体(也叫立方体)。
2、正方体特征:
(1)正方形有6个面,6个面是完全相同的正方形。
(2)正方体有12条棱,它们的长度都相等。
(3)有8个顶点。
【例5】用( )个同样大小的小正方体可以拼成一个大正方体。
用相同的小正方体拼大正方体时,每条边上至少需要2个小正方体,则大正方体至少需要小正方体的数量为:2×2×2=8(个)。
8
【例6】把一个长20厘米,宽16厘米,高9厘米的长方体切成一个尽可能大的正方体,则这个正方体的棱长是( )厘米。
要把一个长方体切成一个尽可能大的正方体,那么这个正方体的棱长应该等于长方体的长、宽、高中的最短棱长,即9厘米。
9
长方体和正方体的异同点
立体 图形 相同点 不同点 面 棱 顶点 面 棱
长方体
正方体
6个
12条
8个
相对的4条棱的长度相等
12条棱的长度都相等
6个长方形(或有2个正方形和4个长方形)
6个完全相同的正方形
1、长方体和正方体的关系
正方体是长、宽、高都相等的长方体。
2、正方体的棱长计算
正方体的棱长总和=棱长×12
正方体的棱长=棱长总和÷12
正方体的棱长计算
【例7】用一根长72厘米的铁丝刚好可以做成一个正方体框架,这个正方体的棱长是( )厘米。
正方体的棱长=棱长总和÷12
72÷12=6(厘米)
6
2
长方体和正方体的表面积
1、长方体的展开图
(1)上、下每个面的长=长方体的长,
宽=长方体的宽;
(2)前、后每个面的长=长方体的长,
宽=长方体的高;
(3)左、右每个面的长=长方体的宽,
宽=长方体的高。
正方体的展开图
常见的正方体展开图类型:
“1-4-1”型:有3行,每行分别有1个、4个、1个小正方形,共六种。
“2-3-1”型:有3行,每行分别有2个、3个、1个小正方形,共三种。
“2-2-2”型:有3行,每行都有2个小正方形,只有一种。
“3-3”型:有2行,每行都有3个小正方形,只有一种。
A选项是“2-2-2”型,可以拼成一个正方体。
B和C均不符合正方体展开图的情况。
【例8】下面各图形中能拼成一个正方体的是( )。
A、 B、 C、
A
任何正方体的展开图都不可能是“田字型”,也不可能是“凹字型”。
以数字2所在面为前面,则数字1所在面为左面,数字4所在面为右面,数字3所在面为上面,数字5所在面为底面,数字6所在面为后面。所以与数字2对面的面是数字6。
【例9】右图是一个正方体盒子的展开图,与数字2对面的面是数字( )。
6
1、长方体或正方体6个面的总面积,叫做它的表面积。
2、长方体的表面积
长方体的表面积=(长×宽+长×高+宽×高)×2
用字母表示:S=(ab+ah+bh)×2
3、正方体的表面积
正方体的表面积=棱长×棱长×6
用字母表示:S=6a2
长方体的表面积
【例10】要在一个长30厘米,宽20厘米,高15厘米,长方体框架的外部全部贴上包装纸,需要( )平方厘米的包装纸。
长方体的表面积=(长×宽+长×高+宽×高)×2
(30×20+20×15+30×15)×2
=(600+300+450)×2
=1350×2
=2700(平方厘米)
9
【例11】用两个长5cm、宽3cm、高2cm的长方体拼成一个大长方体,则大长方体的表面积最大是( )cm ,最小是( )cm 。
长:5×2=10(cm)
(10×2+10×3+2×3)×2
=(20+30+6)×2
=112 (cm2)
112
高:2+2=4(cm)
(5×3+5×4+4×3)×2
=(15+20+12)×2
=94 (cm2)
94
【例12】要制作一个长5分米,宽4分米,高3分米的无盖玻璃鱼缸,需要( )平方分米的玻璃。
玻璃鱼缸的表面积=长方体的表面积-长×宽
(5×3+5×4+3×4)×2-5×4
=(15+20+12)×2-20
=94-20
=74(平方分米)
74
在计算长方体或正方体的表面积时,要注意数清楚面的个数。
正方体的表面积
【例13】已知一个正方体的所有棱长之和是60分米,则它的表面积是( )平方分米。
正方体的棱长=棱长总和÷12
60÷12=5(分米)
正方体的表面积=棱长×棱长×6
5×5×6
=25×6
=150(平方分米)
150
【例14】有两根同样长的铁丝,嘉嘉用其中的一根做成了一个长10厘米、宽8厘米、高6厘米的长方体灯笼框架,用另一根做成一个正方体灯笼框架。
(1)正方体框架的棱长是多少厘米?
长方体的棱长总和=(长+宽+高)×4
(10+8+6)×4
=24×4
=96(厘米)
正方体的棱长=棱长总和÷12
96÷12=8(厘米)
答:正方体框架的棱长是8厘米。
【例14】有两根同样长的铁丝,嘉嘉用其中的一根做成了一个长10厘米、宽8厘米、高6厘米的长方体灯笼框架,用另一根做成一个正方体灯笼框架。
(2)如果把这两个框架的各个面都贴上彩纸,哪个用的彩纸多?
长方体的表面积=(长×宽+长×高+宽×高)×2
(10×8+10×6+8×6)×2
=(80+60+48)×2
=188×2
=376(平方厘米)
正方体的表面积=棱长×棱长×6
8×8×6=384(平方厘米)
376<384
答:正方体框架用的彩纸多。
组合体的表面积
【例15】求出下面立体图形的表面积。(单位:厘米)
正方体的表面积=棱长×棱长×6
8×8×6
=64×6
=384(平方厘米)
求不规则图形的表面积,可以采用“割补法”。
3
长方体和正方体的体积
1、物体所占空间的大小叫做物体的体积。
2、常用的体积单位有立方厘米(cm3)、立方分米(dm3)和立方米(m3)。
3、长方体的体积=长×宽×高
用字母表示:V=abh
4、正方体的体积=棱长×棱长×棱长
用字母表示:V=a3
长方体的体积
【例16】有30立方米的沙子,全部堆在一个长4米、宽2.5米的沙坑里,可以堆多高?
高=长方体的体积÷长÷宽
30÷4÷2.5
=7.5÷2.5
=3(米)
答:可以堆3米。
【例17】将一根长18分米的长方体钢材截成2段,表面积比原来增加了1.2平方分米,原来这根木料的体积是( )立方分米。
将一根长方体钢材截成2段,则表面积增加了2个底面的面积,则底面面积为:1.2÷2=0.6(平方分米)。
长方体的体积=底面积×高,已知长方体钢材长18分米,即高为18分米,则原来这根木料的体积为:
0.6×18=10.8(立方分米)
10.8
正方体的体积
【例18】有一个棱长总和是42厘米的正方体,它的表面积是( )平方厘米,体积是( )立方厘米。
正方体的棱长=棱长总和÷12
42÷12=3.5(厘米)
正方体的表面积=棱长×棱长×6
3.5×3.5×6
=12.25×6
=73.5(平方厘米)
正方体的体积=棱长×棱长×棱长
3.5×3.5×3.5
=12.25×3.5
=42.875(立方厘米)
73.5
42.875
根据排水法可知,石块的体积等于它排开的水的体积。
正方体的体积=棱长×棱长×棱长
10×10×10
=10×10
=1000(立方厘米)
高=长方体的体积÷长÷宽
1000÷20÷10
=50÷10
=5(厘米)
15+5=20(厘米)
【例19】将一个棱长是10cm的正方体石块放入右图的长方体鱼缸中,石块完全浸入水中。此时水面高多少厘米?
1、体积单位间的进率
1立方分米=1000立方厘米;1立方米=1000立方分米。
相邻的两个体积单位间的进率是1000。
2、容器所能容纳物体的体积,通常叫做它们的容积。
3、计量容积,一般用体积单位。计量液体的体积,如水、油等,常用容积单位升和毫升,也可以写作L或mL。
4、容积单位的换算:1升=1000毫升;
容积单位和体积单位的关系:1升=1立方分米;1毫升=1立方厘米。
体积单位和容积单位
【例20】把5升的果汁倒入容积是200毫升的玻璃杯里,可以装满( )杯。
1升=1000毫升
5升=5000毫升
杯子的数量=果汁的容积÷一个玻璃杯的容积
5000÷200=25(杯)
所以,可以装满25杯。
25
【例21】往一个长30厘米、宽15厘米、高15厘米的长方体空鱼缸中倒入3.6升水后,水面离鱼缸口还有( )厘米。
1升=1000立方厘米
3.6×1000=3600(立方厘米)
高=长方体的体积÷长÷宽
水面的高度为:3600÷30÷15=8(厘米)
15-8=7(厘米)
所以,水面离鱼缸口还有7厘米。
7
1、在括号里填上合适的单位名称。
一个保温瓶的容积约是680( );
一个纸巾盒的体积约是3( );
一瓶果汁的容积约是500( );
一个冰箱的容积约是450( )。
2、填空。
0.26m3=( )dm3;8cm3=( )mL=( )L。
毫升
立方厘米
毫升
升
260
8
0.008
3、如果把一个长方体的长、宽、高分别扩大到原来的3倍,那么这个长方体的体积扩大到原来的( )倍。A、3 B、9 C、27
4、一个长9厘米,宽7厘米,高7厘米的长方体,它的表面积是( )平方厘米。
A、380 B、350 C、330
C
B
5、把一个棱长为6厘米的正方体橡皮泥块重新捏成一个底面积为48平方厘米的长方体橡皮泥块,则长方体橡皮泥块的高是多少厘米?
正方体的体积为:6×6×6=216(立方厘米)
长方体的高为:216÷48=4.5(厘米)
答:长方体橡皮泥块的高是4.5厘米。
每一份努力,都将在学习中得到最好的回报。加油!
长方体和正方体
复习专题
人教版五年级数学下册
1
长方体和正方体的认识
2
长方体和正方体的表面积
3
长方体和正方体的体积
长方体和正方体
长方体和正方体的认识
长方体的特征
长方体的棱长计算
正方体的特征
长方体和正方体的表面积
长方体和正方体的展开图
长方体的表面积
正方体的表面积
长方体和正方体的体积
长方体的体积
正方体的体积
体积单位和容积单位
长方体
正方体
正方体的棱长计算
组合图形的表面积
1、认识长方体
一般是由6个长方形(特殊情况有两个相对的面是正方形)围成的立体图形叫做长方体。
相交于同一顶点的3条棱的长度分别叫作长方体的长、宽、高。
1
长方体和正方体的认识
面
棱:面和面相交的线段
顶点:棱和棱的交点
长
高
宽
长方体的特征
(1)面:长方体有6个面,这6个面一般是长方形的,特殊情况有两个相对的面是正方形;相对的面完全相同。
(2)棱:长方体有12条棱,相对的棱长度相等。长方体12条棱可以分成3组,分别有4条长、4条宽、4条高。
(3)顶点:长方体有8个顶点。
【例1】辨一辨。 (对的画“√”,错的画“×”)
(1)一个长方体至少有4个面是长方形。( )
(1)一个长方体有6个面,一般情况下六个面都是长方形。
特殊情况时有两个面是正方形,其他四个面都是长方形,并且这四个面完全相同。原题说法正确。
√
【例1】辨一辨。 (对的画“√”,错的画“×”)
(2)把一个长方体截成两个小长方体后,截面不可能是正方形。( )
(2)如果一个长方体有两个面是正方形,其他四个面都是长方形。这样的长方体截成两个小长方体,截面就是正方形,所以原题说法错误。
×
【例1】辨一辨。 (对的画“√”,错的画“×”)
(3)有6个面、12条棱、8个顶点的立体图形都是长方体。( )
(3)有6个面、12条棱、8个顶点的立体图形不都是长方体,也可能是其他立体图形,如棱台,所以原题说法错误。
×
根据长方体的特征:长方体有12条棱,相对的四条棱长度相等,按长度可分为长、宽、高三组,每一组有4条棱。如果长方体的六个面中有两个面是相同的正方形,此时12条棱中有8条棱的长度相等,另外4条棱的长度相等。
A
【例2】下面3组木棒,( )不可以搭成一个长方体框架。
A、 B、 C、
长方体的棱长计算
长方体的棱长总和=(长+宽+高)×4
=长×4+宽×4+高×4
长=棱长总和÷4-宽-高
宽=棱长总和÷4-长-高
高=棱长总和÷4-长-宽
【例3】乾乾用小木棒制作了一个长方体花灯框架,这个长方体同一顶点上的三根木棒长度分别为25cm、18cm和12cm,则一共用了( )cm的木棒。
长方体的棱长总和=(长+宽+高)×4
(25+18+12)×4
=55×4
=220(cm)
220
【例4】给一个长1.8米,宽0.6米的玻璃柜台各边安上角铁,一共用去了15.2米的角铁,那么这个玻璃柜台的高是多少米?
高=棱长总和÷4-长-宽
15.2÷4-1.8-0.6
=3.8-1.8-0.6
=1.4(米)
答:这个玻璃柜台的高是1.4米。
认识正方体
1、认识正方体
由6个完全相同的正方形围成的立体图形叫做正方体(也叫立方体)。
2、正方体特征:
(1)正方形有6个面,6个面是完全相同的正方形。
(2)正方体有12条棱,它们的长度都相等。
(3)有8个顶点。
【例5】用( )个同样大小的小正方体可以拼成一个大正方体。
用相同的小正方体拼大正方体时,每条边上至少需要2个小正方体,则大正方体至少需要小正方体的数量为:2×2×2=8(个)。
8
【例6】把一个长20厘米,宽16厘米,高9厘米的长方体切成一个尽可能大的正方体,则这个正方体的棱长是( )厘米。
要把一个长方体切成一个尽可能大的正方体,那么这个正方体的棱长应该等于长方体的长、宽、高中的最短棱长,即9厘米。
9
长方体和正方体的异同点
立体 图形 相同点 不同点 面 棱 顶点 面 棱
长方体
正方体
6个
12条
8个
相对的4条棱的长度相等
12条棱的长度都相等
6个长方形(或有2个正方形和4个长方形)
6个完全相同的正方形
1、长方体和正方体的关系
正方体是长、宽、高都相等的长方体。
2、正方体的棱长计算
正方体的棱长总和=棱长×12
正方体的棱长=棱长总和÷12
正方体的棱长计算
【例7】用一根长72厘米的铁丝刚好可以做成一个正方体框架,这个正方体的棱长是( )厘米。
正方体的棱长=棱长总和÷12
72÷12=6(厘米)
6
2
长方体和正方体的表面积
1、长方体的展开图
(1)上、下每个面的长=长方体的长,
宽=长方体的宽;
(2)前、后每个面的长=长方体的长,
宽=长方体的高;
(3)左、右每个面的长=长方体的宽,
宽=长方体的高。
正方体的展开图
常见的正方体展开图类型:
“1-4-1”型:有3行,每行分别有1个、4个、1个小正方形,共六种。
“2-3-1”型:有3行,每行分别有2个、3个、1个小正方形,共三种。
“2-2-2”型:有3行,每行都有2个小正方形,只有一种。
“3-3”型:有2行,每行都有3个小正方形,只有一种。
A选项是“2-2-2”型,可以拼成一个正方体。
B和C均不符合正方体展开图的情况。
【例8】下面各图形中能拼成一个正方体的是( )。
A、 B、 C、
A
任何正方体的展开图都不可能是“田字型”,也不可能是“凹字型”。
以数字2所在面为前面,则数字1所在面为左面,数字4所在面为右面,数字3所在面为上面,数字5所在面为底面,数字6所在面为后面。所以与数字2对面的面是数字6。
【例9】右图是一个正方体盒子的展开图,与数字2对面的面是数字( )。
6
1、长方体或正方体6个面的总面积,叫做它的表面积。
2、长方体的表面积
长方体的表面积=(长×宽+长×高+宽×高)×2
用字母表示:S=(ab+ah+bh)×2
3、正方体的表面积
正方体的表面积=棱长×棱长×6
用字母表示:S=6a2
长方体的表面积
【例10】要在一个长30厘米,宽20厘米,高15厘米,长方体框架的外部全部贴上包装纸,需要( )平方厘米的包装纸。
长方体的表面积=(长×宽+长×高+宽×高)×2
(30×20+20×15+30×15)×2
=(600+300+450)×2
=1350×2
=2700(平方厘米)
9
【例11】用两个长5cm、宽3cm、高2cm的长方体拼成一个大长方体,则大长方体的表面积最大是( )cm ,最小是( )cm 。
长:5×2=10(cm)
(10×2+10×3+2×3)×2
=(20+30+6)×2
=112 (cm2)
112
高:2+2=4(cm)
(5×3+5×4+4×3)×2
=(15+20+12)×2
=94 (cm2)
94
【例12】要制作一个长5分米,宽4分米,高3分米的无盖玻璃鱼缸,需要( )平方分米的玻璃。
玻璃鱼缸的表面积=长方体的表面积-长×宽
(5×3+5×4+3×4)×2-5×4
=(15+20+12)×2-20
=94-20
=74(平方分米)
74
在计算长方体或正方体的表面积时,要注意数清楚面的个数。
正方体的表面积
【例13】已知一个正方体的所有棱长之和是60分米,则它的表面积是( )平方分米。
正方体的棱长=棱长总和÷12
60÷12=5(分米)
正方体的表面积=棱长×棱长×6
5×5×6
=25×6
=150(平方分米)
150
【例14】有两根同样长的铁丝,嘉嘉用其中的一根做成了一个长10厘米、宽8厘米、高6厘米的长方体灯笼框架,用另一根做成一个正方体灯笼框架。
(1)正方体框架的棱长是多少厘米?
长方体的棱长总和=(长+宽+高)×4
(10+8+6)×4
=24×4
=96(厘米)
正方体的棱长=棱长总和÷12
96÷12=8(厘米)
答:正方体框架的棱长是8厘米。
【例14】有两根同样长的铁丝,嘉嘉用其中的一根做成了一个长10厘米、宽8厘米、高6厘米的长方体灯笼框架,用另一根做成一个正方体灯笼框架。
(2)如果把这两个框架的各个面都贴上彩纸,哪个用的彩纸多?
长方体的表面积=(长×宽+长×高+宽×高)×2
(10×8+10×6+8×6)×2
=(80+60+48)×2
=188×2
=376(平方厘米)
正方体的表面积=棱长×棱长×6
8×8×6=384(平方厘米)
376<384
答:正方体框架用的彩纸多。
组合体的表面积
【例15】求出下面立体图形的表面积。(单位:厘米)
正方体的表面积=棱长×棱长×6
8×8×6
=64×6
=384(平方厘米)
求不规则图形的表面积,可以采用“割补法”。
3
长方体和正方体的体积
1、物体所占空间的大小叫做物体的体积。
2、常用的体积单位有立方厘米(cm3)、立方分米(dm3)和立方米(m3)。
3、长方体的体积=长×宽×高
用字母表示:V=abh
4、正方体的体积=棱长×棱长×棱长
用字母表示:V=a3
长方体的体积
【例16】有30立方米的沙子,全部堆在一个长4米、宽2.5米的沙坑里,可以堆多高?
高=长方体的体积÷长÷宽
30÷4÷2.5
=7.5÷2.5
=3(米)
答:可以堆3米。
【例17】将一根长18分米的长方体钢材截成2段,表面积比原来增加了1.2平方分米,原来这根木料的体积是( )立方分米。
将一根长方体钢材截成2段,则表面积增加了2个底面的面积,则底面面积为:1.2÷2=0.6(平方分米)。
长方体的体积=底面积×高,已知长方体钢材长18分米,即高为18分米,则原来这根木料的体积为:
0.6×18=10.8(立方分米)
10.8
正方体的体积
【例18】有一个棱长总和是42厘米的正方体,它的表面积是( )平方厘米,体积是( )立方厘米。
正方体的棱长=棱长总和÷12
42÷12=3.5(厘米)
正方体的表面积=棱长×棱长×6
3.5×3.5×6
=12.25×6
=73.5(平方厘米)
正方体的体积=棱长×棱长×棱长
3.5×3.5×3.5
=12.25×3.5
=42.875(立方厘米)
73.5
42.875
根据排水法可知,石块的体积等于它排开的水的体积。
正方体的体积=棱长×棱长×棱长
10×10×10
=10×10
=1000(立方厘米)
高=长方体的体积÷长÷宽
1000÷20÷10
=50÷10
=5(厘米)
15+5=20(厘米)
【例19】将一个棱长是10cm的正方体石块放入右图的长方体鱼缸中,石块完全浸入水中。此时水面高多少厘米?
1、体积单位间的进率
1立方分米=1000立方厘米;1立方米=1000立方分米。
相邻的两个体积单位间的进率是1000。
2、容器所能容纳物体的体积,通常叫做它们的容积。
3、计量容积,一般用体积单位。计量液体的体积,如水、油等,常用容积单位升和毫升,也可以写作L或mL。
4、容积单位的换算:1升=1000毫升;
容积单位和体积单位的关系:1升=1立方分米;1毫升=1立方厘米。
体积单位和容积单位
【例20】把5升的果汁倒入容积是200毫升的玻璃杯里,可以装满( )杯。
1升=1000毫升
5升=5000毫升
杯子的数量=果汁的容积÷一个玻璃杯的容积
5000÷200=25(杯)
所以,可以装满25杯。
25
【例21】往一个长30厘米、宽15厘米、高15厘米的长方体空鱼缸中倒入3.6升水后,水面离鱼缸口还有( )厘米。
1升=1000立方厘米
3.6×1000=3600(立方厘米)
高=长方体的体积÷长÷宽
水面的高度为:3600÷30÷15=8(厘米)
15-8=7(厘米)
所以,水面离鱼缸口还有7厘米。
7
1、在括号里填上合适的单位名称。
一个保温瓶的容积约是680( );
一个纸巾盒的体积约是3( );
一瓶果汁的容积约是500( );
一个冰箱的容积约是450( )。
2、填空。
0.26m3=( )dm3;8cm3=( )mL=( )L。
毫升
立方厘米
毫升
升
260
8
0.008
3、如果把一个长方体的长、宽、高分别扩大到原来的3倍,那么这个长方体的体积扩大到原来的( )倍。A、3 B、9 C、27
4、一个长9厘米,宽7厘米,高7厘米的长方体,它的表面积是( )平方厘米。
A、380 B、350 C、330
C
B
5、把一个棱长为6厘米的正方体橡皮泥块重新捏成一个底面积为48平方厘米的长方体橡皮泥块,则长方体橡皮泥块的高是多少厘米?
正方体的体积为:6×6×6=216(立方厘米)
长方体的高为:216÷48=4.5(厘米)
答:长方体橡皮泥块的高是4.5厘米。
每一份努力,都将在学习中得到最好的回报。加油!
