数学人教A版(2019)选择性必修第三册6.3.2二项式系数的性质 课件(共18张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第三册6.3.2二项式系数的性质 课件(共18张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-11 10:22:59 | ||
图片预览






文档简介
(共18张PPT)
6.3.2 二项式系数的性质
第六章 计数原理
努力创造适合每一位学生发展的教育
---------------------------------------------
难点:会用“赋值法”求展开式系数的和.
重点:能记住二项式系数的性质,并能解决相关问题.
努力创造适合每一位学生发展的教育
一、复习引入
(a+b)n=
1、二项式定理
展开式中一共有n+1项.
2、二项展开式的通项
an-kbk
3、二项式的系数
Cn
0
Cn
1
Cn
k
Cn
n
…
…
4、二项式的系数的和
+ + + … + +… +=
Cn
0
Cn
1
Cn
2
Cn
k
Cn
n
2n
努力创造适合每一位学生发展的教育
二、探究新知
的展开式的二项式系数有很多有趣性质,我可以不同角度进行研究.
问题1:(a+b)1,(a+b)2,(a+b)3,(a+b)4,(a+b)5,(a+b)6的展开式中的二项式系数分别是哪些 并将它们的计算结果填入下表:
6
5
4
3
2
1
二项式系数
n
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
追问1:观察上表中每一行的数据,你发现了什么规律吗?
努力创造适合每一位学生发展的教育
二、探究新知
为了便于发现规律,将上表写成如下形式,你又能发现这些数据有什么新的规律吗
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
实验提示:
(1)从左至右横行来看
(2)从上下相邻行来看
(3)请计算每行的和看
努力创造适合每一位学生发展的教育
三、学生探索
(1)从左至右横行来看,有什么规律?
在同一行中,每行两端都是1,与这两个1等距离的项的系数相等.
性质1:对称性:
性质2 增减性与最大值
二项式系数前半部分是逐渐增大的,它的后半部分是逐渐减小的,且中间项一个或者两个值最大。
∴(1)当n为偶数时,正中间一项的二项式系数最大;
(2)当n为奇数时,中间两项的二项式系数同时取得最大值.
努力创造适合每一位学生发展的教育
三、学生探索
问题4 可以从函数图像的角度分析以上性质吗?
r
f(r)
O
1
2
3
5
10
15
20
4
5
6
对于 的展开式的各二项式系数中 Cnr可看成是以r为自变量的函数 f (r),其定义域是:
当n=6 时,f (r)=C6r (r∈{0, 1, 2, 3, 4, 5, 6})的图象。
从图像上发现:
1.函数图像是 个孤立的点;
2.对称轴是r= ;
3.直观看出二项式系数值具有:
4.在r= 处取得最大值,f( )=
7
3
3
3
20
先增后减
努力创造适合每一位学生发展的教育
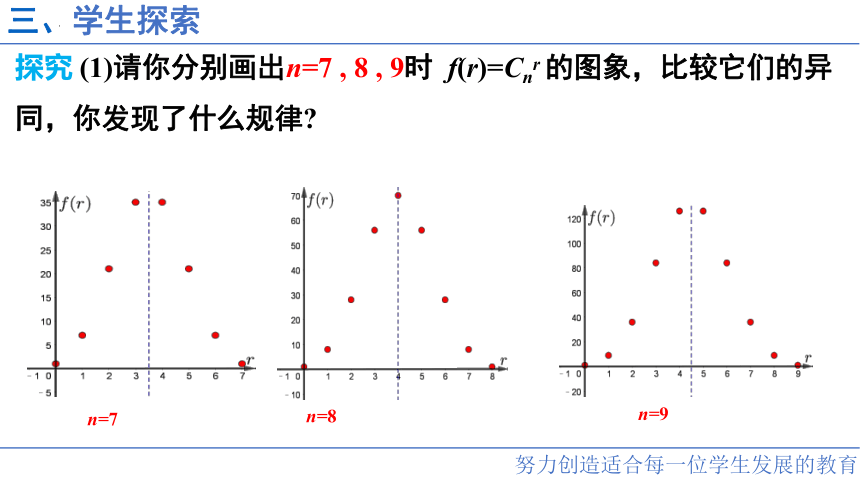
探究 (1)请你分别画出n=7 , 8 , 9时 f(r)=Cnr 的图象,比较它们的异同,你发现了什么规律
n=7
n=8
n=9
三、学生探索
努力创造适合每一位学生发展的教育
三、学生探索
问题5:你能从数的角度证明二项式系数性质(1)和(2)吗?
性质1:对称性
这一性质可直接由公式 得到.
与首末两端“等距离”的两个二项式系数相等.
追问1:从数的角度我们可以通过比值比较两个数的大小
性质2:增减性与最大值
(增减性的实质是比较 的大小)
由:
可知,当 时,
二项式系数是逐渐增大的,
由对称性可知它的后半部分是逐渐减小的,且中间项取得最大值
努力创造适合每一位学生发展的教育
性质2:增减性与最大值
∴(1)当n为偶数时,正中间一项的二项式系数 最大;
(2)当n为奇数时,中间两项的二项式系数 相等,且同时取得最大值.
∵二项展开式共有n+1项,
f (k)
k
n
3
O
5
15
20
1
10
1
2
4
5
n为偶数
f (r)
r
n
O
5
15
20
1
10
n为奇数
三、学生探索
努力创造适合每一位学生发展的教育
三、学生探索
求证:(a+b)n 的展开式中的所有二项式系数的和等于 .
性质3: 各二项式系数的和
令x =1,得
另证:
结论:
组合总数公式
思考
结合二项式系数和为2n
努力创造适合每一位学生发展的教育
性质4:
三、学生探索
努力创造适合每一位学生发展的教育
性质5:
三、学生探索
研究斜行规律:
……
一般地,
努力创造适合每一位学生发展的教育斐波那契数列问题:写出斜线上各行数字的和,有什么规律?25……1381321第1行1 1第5行1 5 10 10 5 1第6行1 6 15 20 15 6 1第7行1 7 21 35 35 21 7 1第2行1 2 1第3行1 3 3 1第4行1 4 6 4 1第8行1 8 28 56 70 56 28 8 1第0行134努力创造适合每一位学生发展的教育
四、例题展示
性质1:对称性
例1:在的展开式中,第3项和第4项的二项式系数相等,展开式中的系数是( )
变式1:求证:
练习1:的展开式中第3项与第7项的二项式系数相等,含一的项的系数为 (用数字作答).
努力创造适合每一位学生发展的教育
四、例题展示
性质2:增减性与最大值
例2:展开式中各项的系数和比各项的二项式系数和大992求:
(1)展开式中二项式系数的最大项
(2)求展开式中系数最大的项
变式2:在的展开式中,
(1)求二项式系数最大的项;
(2)求系数最大的项;
(3)求系数最小的项;
(4)系数的绝对值最大的项是第几项
努力创造适合每一位学生发展的教育
四、例题展示
性质3: 各二项式系数的和
例3:在的二项展开式中,( );所有二项式系数和为( );所有项的系数和( ).
变式1:已知,则:
(1) =( );
(2)( ).
练习2:已知多项式可以写成,则( )
努力创造适合每一位学生发展的教育
四、例题展示
变式2:已知(x∈R),求:
(1)的值;
(2)值;
(3) 的值
练习3:若,的值为( )
努力创造适合每一位学生发展的教育
五、课堂小结
性质1:对称性
性质2:增减性与最大值
性质3: 各二项式系数的和
性质4:
性质5:
6.3.2 二项式系数的性质
第六章 计数原理
努力创造适合每一位学生发展的教育
---------------------------------------------
难点:会用“赋值法”求展开式系数的和.
重点:能记住二项式系数的性质,并能解决相关问题.
努力创造适合每一位学生发展的教育
一、复习引入
(a+b)n=
1、二项式定理
展开式中一共有n+1项.
2、二项展开式的通项
an-kbk
3、二项式的系数
Cn
0
Cn
1
Cn
k
Cn
n
…
…
4、二项式的系数的和
+ + + … + +… +=
Cn
0
Cn
1
Cn
2
Cn
k
Cn
n
2n
努力创造适合每一位学生发展的教育
二、探究新知
的展开式的二项式系数有很多有趣性质,我可以不同角度进行研究.
问题1:(a+b)1,(a+b)2,(a+b)3,(a+b)4,(a+b)5,(a+b)6的展开式中的二项式系数分别是哪些 并将它们的计算结果填入下表:
6
5
4
3
2
1
二项式系数
n
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
追问1:观察上表中每一行的数据,你发现了什么规律吗?
努力创造适合每一位学生发展的教育
二、探究新知
为了便于发现规律,将上表写成如下形式,你又能发现这些数据有什么新的规律吗
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
实验提示:
(1)从左至右横行来看
(2)从上下相邻行来看
(3)请计算每行的和看
努力创造适合每一位学生发展的教育
三、学生探索
(1)从左至右横行来看,有什么规律?
在同一行中,每行两端都是1,与这两个1等距离的项的系数相等.
性质1:对称性:
性质2 增减性与最大值
二项式系数前半部分是逐渐增大的,它的后半部分是逐渐减小的,且中间项一个或者两个值最大。
∴(1)当n为偶数时,正中间一项的二项式系数最大;
(2)当n为奇数时,中间两项的二项式系数同时取得最大值.
努力创造适合每一位学生发展的教育
三、学生探索
问题4 可以从函数图像的角度分析以上性质吗?
r
f(r)
O
1
2
3
5
10
15
20
4
5
6
对于 的展开式的各二项式系数中 Cnr可看成是以r为自变量的函数 f (r),其定义域是:
当n=6 时,f (r)=C6r (r∈{0, 1, 2, 3, 4, 5, 6})的图象。
从图像上发现:
1.函数图像是 个孤立的点;
2.对称轴是r= ;
3.直观看出二项式系数值具有:
4.在r= 处取得最大值,f( )=
7
3
3
3
20
先增后减
努力创造适合每一位学生发展的教育
探究 (1)请你分别画出n=7 , 8 , 9时 f(r)=Cnr 的图象,比较它们的异同,你发现了什么规律
n=7
n=8
n=9
三、学生探索
努力创造适合每一位学生发展的教育
三、学生探索
问题5:你能从数的角度证明二项式系数性质(1)和(2)吗?
性质1:对称性
这一性质可直接由公式 得到.
与首末两端“等距离”的两个二项式系数相等.
追问1:从数的角度我们可以通过比值比较两个数的大小
性质2:增减性与最大值
(增减性的实质是比较 的大小)
由:
可知,当 时,
二项式系数是逐渐增大的,
由对称性可知它的后半部分是逐渐减小的,且中间项取得最大值
努力创造适合每一位学生发展的教育
性质2:增减性与最大值
∴(1)当n为偶数时,正中间一项的二项式系数 最大;
(2)当n为奇数时,中间两项的二项式系数 相等,且同时取得最大值.
∵二项展开式共有n+1项,
f (k)
k
n
3
O
5
15
20
1
10
1
2
4
5
n为偶数
f (r)
r
n
O
5
15
20
1
10
n为奇数
三、学生探索
努力创造适合每一位学生发展的教育
三、学生探索
求证:(a+b)n 的展开式中的所有二项式系数的和等于 .
性质3: 各二项式系数的和
令x =1,得
另证:
结论:
组合总数公式
思考
结合二项式系数和为2n
努力创造适合每一位学生发展的教育
性质4:
三、学生探索
努力创造适合每一位学生发展的教育
性质5:
三、学生探索
研究斜行规律:
……
一般地,
努力创造适合每一位学生发展的教育斐波那契数列问题:写出斜线上各行数字的和,有什么规律?25……1381321第1行1 1第5行1 5 10 10 5 1第6行1 6 15 20 15 6 1第7行1 7 21 35 35 21 7 1第2行1 2 1第3行1 3 3 1第4行1 4 6 4 1第8行1 8 28 56 70 56 28 8 1第0行134努力创造适合每一位学生发展的教育
四、例题展示
性质1:对称性
例1:在的展开式中,第3项和第4项的二项式系数相等,展开式中的系数是( )
变式1:求证:
练习1:的展开式中第3项与第7项的二项式系数相等,含一的项的系数为 (用数字作答).
努力创造适合每一位学生发展的教育
四、例题展示
性质2:增减性与最大值
例2:展开式中各项的系数和比各项的二项式系数和大992求:
(1)展开式中二项式系数的最大项
(2)求展开式中系数最大的项
变式2:在的展开式中,
(1)求二项式系数最大的项;
(2)求系数最大的项;
(3)求系数最小的项;
(4)系数的绝对值最大的项是第几项
努力创造适合每一位学生发展的教育
四、例题展示
性质3: 各二项式系数的和
例3:在的二项展开式中,( );所有二项式系数和为( );所有项的系数和( ).
变式1:已知,则:
(1) =( );
(2)( ).
练习2:已知多项式可以写成,则( )
努力创造适合每一位学生发展的教育
四、例题展示
变式2:已知(x∈R),求:
(1)的值;
(2)值;
(3) 的值
练习3:若,的值为( )
努力创造适合每一位学生发展的教育
五、课堂小结
性质1:对称性
性质2:增减性与最大值
性质3: 各二项式系数的和
性质4:
性质5:
