吉林省油田第十二中学2023-2024学年第二学期九年级数学开学考试试卷(无答案)
文档属性
| 名称 | 吉林省油田第十二中学2023-2024学年第二学期九年级数学开学考试试卷(无答案) | 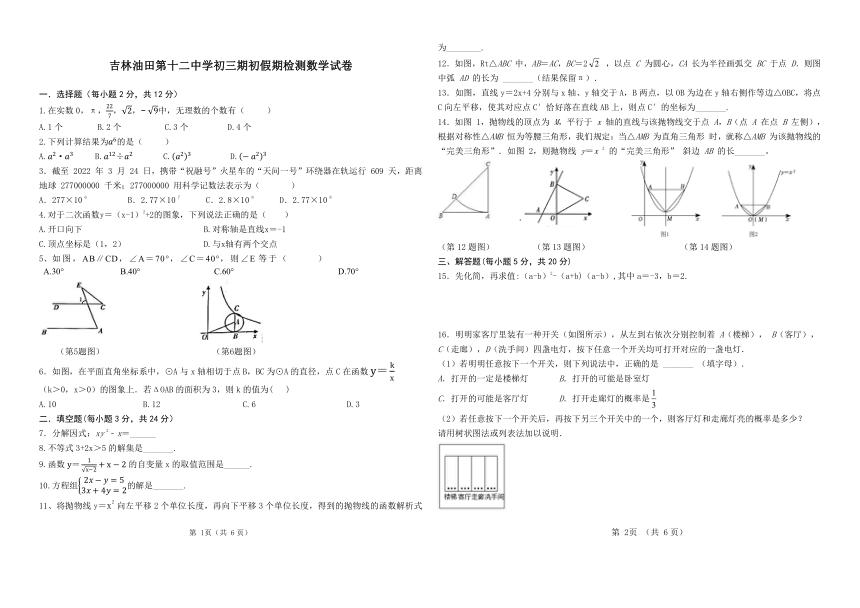 | |
| 格式 | docx | ||
| 文件大小 | 246.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-11 09:51:50 | ||
图片预览

文档简介
吉林油田第十二中学初三期初假期检测数学试卷
一.选择题(每小题2分,共12分)
1.在实数0,π,,,中,无理数的个数有( )
A.1个 B.2个 C.3个 D.4个
2.下列计算结果为的是( )
A.· B.÷ C. D.
3.截至 2022 年 3 月 24 日,携带“祝融号”火星车的“天问一号”环绕器在轨运行 609 天,距离地球 277000000 千米;277000000 用科学记数法表示为( )
A.277×10 6 B.2.77×10 7 C.2.8×10 8 D.2.77×10 8
4.对于二次函数y=(x-1)2+2的图象,下列说法正确的是( )
A.开口向下 B.对称轴是直线x=-1
C.顶点坐标是(1,2) D.与x轴有两个交点
5、如图,AB∥CD,∠A=70°,∠C=40°,则∠E等于( )
A.30° B.40° C.60° D.70°
(第5题图) (第6题图)
如图,在平面直角坐标系中,⊙A与x轴相切于点B,BC为⊙A的直径,点C在函数
(k>0,x>0)的图象上.若ΔOAB的面积为3,则k的值为( )
A.10 B.12 C.6 D.3
二.填空题(每小题3分,共24分)
7.分解因式:xy 2﹣x=______
8.不等式3+2x>5的解集是_______.
9.函数的自变量x的取值范围是______.
10.方程组的解是_______.
11、将抛物线y=x2 向左平移2个单位长度,再向下平移3个单位长度,得到的抛物线的函数解析式为________.
12.如图,Rt△ABC 中,AB=AC,BC=2 ,以点 C 为圆心,CA 长为半径画弧交 BC 于点 D.则图中弧 AD 的长为 _______(结果保留π).
13.如图,直线y=2x+4分别与x轴、y轴交于A,B两点,以OB为边在y轴右侧作等边△OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为_______.
14.如图 1,抛物线的顶点为 M,平行于 x 轴的直线与该抛物线交于点 A,B(点 A 在点 B 左侧),根据对称性△AMB 恒为等腰三角形,我们规定:当△AMB 为直角三角形 时,就称△AMB 为该抛物线的“完美三角形”.如图 2,则抛物线 y=x 2 的“完美三角形” 斜边 AB 的长_______。
.
(第12题图) (第13题图) (第14题图)
三、解答题(每小题5分,共20分)
15.先化简,再求值:(a-b)2-(a+b)(a-b),其中a=-3,b=2.
16.明明家客厅里装有一种开关(如图所示),从左到右依次分别控制着 A(楼梯), B(客厅),
C(走廊),D(洗手间)四盏电灯,按下任意一个开关均可打开对应的一盏电灯.
(1)若明明任意按下一个开关,则下列说法中,正确的是 _______ (填字母).
A.打开的一定是楼梯灯 B.打开的可能是卧室灯
C.打开的可能是客厅灯 D.打开走廊灯的概率是
(2)若任意按下一个开关后,再按下另三个开关中的一个,则客厅灯和走廊灯亮的概率是多少?
请用树状图法或列表法加以说明.
17.如图,在菱形ABCD中,过点B作BE⊥AD于点E,过点B作BF⊥CD于点F,求证:AE=CF.
18.某校组织“衫衫来了, 爱心义卖 ”活动 ,购进了黑白两种纯色的文化衫共100件 ,进行DIY手绘设计后出售,所获利润全部捐给“幸福村 ”.每种文化衫的成本和售价如表 , 假设文化衫全部售出,共获利720元 ,求购进两种文化衫各多少件
白色文化衫 黑色文化衫
成本(元) 25 28
售价(元) 31 36
四、解答题(每小题7分,共28分)
19. 如图 ,在6×6的方格纸中 , 每个小正方形的边长为1,每个小正方形的顶点称为格点 , 请按要求画出格点三角形与格点四边形 .
(1)在图①中以线段AB 为边画一个格点△ABC,使AB=BC;
(2)在图②中以线段AB为边画一个格点四边形 ABCD,使其面积为7, 且 ∠BAD= 90°.
20.如图,在平面直角坐标系中,直线y=-2x+2与x轴、y轴分别相交于点A,B,四边形ABCD是正方形,双曲线 在第一象限经过点D.
(1)求双曲线表示的函数解析式;
(2)将正方形ABCD沿x轴向左平移_____个单位长度时,点C的对应点
恰好落在(1)中的双曲线上.
21.2022年2月4日晚,当我国运动员迪妮格尔·衣拉木江和赵嘉文将最后一棒火炬嵌入主火炬“大雪花”中央时 ,第24届北京冬奥会向世界展示了低碳环保的“点火”仪式 . 小华 有幸在现场目睹这一过程,在“大雪花 ”竖直升起的某一刻 ,从小华的位置(点 O)观测“大雪花”的顶部 A 的仰角α为 12.8°,底部 B 的俯角β为15.3°,已知“大雪花 ”高 AB 约 14.89m ,求小华的位置离“大雪花”的水平距离 OC.(结果精确到0.1m ,参考数据 :tan12.8°≈0.23,sin12.8°≈0.22,tan15.3≈0.27,
sin15.3°≈0.26)
某校组织学生参加“防疫卫生知识竞赛”(满分为100分).竞赛结束后,随机抽取甲、乙两班各40名学生的成绩,并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息。
a.甲、乙两班40名学生数学成绩的频数分布统计表如下:
成绩 班级 50≤x<60 60≤x<70 70≤x<80 80≤x<90 90≤x≤100
甲 4 11 13 10 2
乙 6 3 15 14 2
(说明:成绩80分及以上为优秀,70--79分为良好,60--69分为合格,60分以下为不合格)
b.甲班成绩在70≤x<80这一组的是:70,70,70,71,72,73,73,73,74,75,76,77,78
c.甲、乙两班成绩的平均分、中位数、众数如下:
班级 平均分 中位数 众数
甲 74.2 n 85
乙 73.5 76 84
根据以上信息,回答下列问题:
(1)写出表中n的值,n= ;
(2)在此次测试中,某学生的成绩是74分,在他所属班级排在前20名,由表中数据可知该学生是________(选填“甲”或“乙”)班的学生,理由是_____________________________________________________;
(3)假设学校1200名学生都参加此次竞赛,估计成绩优秀的学生人数.
五、解答题(每小题8分,共16分)
23.甲乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的关系如图,请根据图像所提供的信息解答下列问题
(1)甲队在开挖后6h内,每小时挖_____m
(2)乙队在2≤x≤6时间段内,求y与x之间的函数关系式
(3)直接写出开挖后几个小时时,甲、乙两队挖的河渠的长度相差5m.
24.(1)如图1 ,在Rt△ABC中,∠ABC=90°,以点B为中心,把△ABC逆时针旋转90°,得到△A1BC1;再以点C为中心,把△ABC顺时针旋转90°,得到△A2B1C,连接C1B1,则C1B1与BC的位置关系为__________;
(2)如图2,当△ABC是锐角三角形,∠ABC=α(α≠60°)时,将△ABC按照(1)中的方式旋转α,连接C1B1,探究C1B1与BC的位置关系,写出你的结论,并加以证明;
(3)如图3 ,在图2 的基础上,连接B1B,若C1B1= BC,△C1BB1的面积为4,则△B1BC的面积为_____.
六、解答题(每小题10分,共20分)
25.如图,在 △ABC 中,∠ACB=90°,AC=8,BC=6,点M 为边AB 的中点.点Q 从点 A 出发,沿AC 方向以每秒1个单位长度的速度向终点C 运动,同时点P 从点C 出发, 以每秒2个单位长度的速度先沿CB 方向运动到点B,再沿BA 方向向终点A 运动,以 MP,MQ 为邻边构造 MQEP,设点Q 运动的时间为t秒.
(1)当点E 落在AC 边上时,求t和 MQEP 的面积;
(2)当点P 在边AB上时,设 MQEP 的面积为S(S >0),求S与t之间的函数关系式;
(3)连接CM,直接写出CM 将 MQEP 分成的两部分图形面积相等时t的值.
26.在平面直角坐标系中,二次函数 y=ax2+bx+2 的图象交 x 轴于点 A(﹣3,0)和点 B(1, 0).
(1)此二次函数的图象与 y 轴的交点的纵坐标为_________ .
(2)求此二次函数的关系式.
(3)当﹣2≤x≤3 时,求二次函数 y=ax2+bx+2 的最大值和最小值.
(4)点 P 为二次函数 y=ax2+bx+2(﹣3<x< )图象上任意一点,其横坐标为 m,过点P作PQ//x轴,点 Q 的横坐标为 ﹣2m﹣4.已知点 P 与点 Q 不重合,且线段 PQ 的长度随 m 的增大而减小.直接写出线段 PQ 与二次函数 y=ax2+bx+2(﹣3<x< )的图象只有 1 个公共点时,m 的取值范围.
第 5页(共 6页) 第 6页 (共 6页)
一.选择题(每小题2分,共12分)
1.在实数0,π,,,中,无理数的个数有( )
A.1个 B.2个 C.3个 D.4个
2.下列计算结果为的是( )
A.· B.÷ C. D.
3.截至 2022 年 3 月 24 日,携带“祝融号”火星车的“天问一号”环绕器在轨运行 609 天,距离地球 277000000 千米;277000000 用科学记数法表示为( )
A.277×10 6 B.2.77×10 7 C.2.8×10 8 D.2.77×10 8
4.对于二次函数y=(x-1)2+2的图象,下列说法正确的是( )
A.开口向下 B.对称轴是直线x=-1
C.顶点坐标是(1,2) D.与x轴有两个交点
5、如图,AB∥CD,∠A=70°,∠C=40°,则∠E等于( )
A.30° B.40° C.60° D.70°
(第5题图) (第6题图)
如图,在平面直角坐标系中,⊙A与x轴相切于点B,BC为⊙A的直径,点C在函数
(k>0,x>0)的图象上.若ΔOAB的面积为3,则k的值为( )
A.10 B.12 C.6 D.3
二.填空题(每小题3分,共24分)
7.分解因式:xy 2﹣x=______
8.不等式3+2x>5的解集是_______.
9.函数的自变量x的取值范围是______.
10.方程组的解是_______.
11、将抛物线y=x2 向左平移2个单位长度,再向下平移3个单位长度,得到的抛物线的函数解析式为________.
12.如图,Rt△ABC 中,AB=AC,BC=2 ,以点 C 为圆心,CA 长为半径画弧交 BC 于点 D.则图中弧 AD 的长为 _______(结果保留π).
13.如图,直线y=2x+4分别与x轴、y轴交于A,B两点,以OB为边在y轴右侧作等边△OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为_______.
14.如图 1,抛物线的顶点为 M,平行于 x 轴的直线与该抛物线交于点 A,B(点 A 在点 B 左侧),根据对称性△AMB 恒为等腰三角形,我们规定:当△AMB 为直角三角形 时,就称△AMB 为该抛物线的“完美三角形”.如图 2,则抛物线 y=x 2 的“完美三角形” 斜边 AB 的长_______。
.
(第12题图) (第13题图) (第14题图)
三、解答题(每小题5分,共20分)
15.先化简,再求值:(a-b)2-(a+b)(a-b),其中a=-3,b=2.
16.明明家客厅里装有一种开关(如图所示),从左到右依次分别控制着 A(楼梯), B(客厅),
C(走廊),D(洗手间)四盏电灯,按下任意一个开关均可打开对应的一盏电灯.
(1)若明明任意按下一个开关,则下列说法中,正确的是 _______ (填字母).
A.打开的一定是楼梯灯 B.打开的可能是卧室灯
C.打开的可能是客厅灯 D.打开走廊灯的概率是
(2)若任意按下一个开关后,再按下另三个开关中的一个,则客厅灯和走廊灯亮的概率是多少?
请用树状图法或列表法加以说明.
17.如图,在菱形ABCD中,过点B作BE⊥AD于点E,过点B作BF⊥CD于点F,求证:AE=CF.
18.某校组织“衫衫来了, 爱心义卖 ”活动 ,购进了黑白两种纯色的文化衫共100件 ,进行DIY手绘设计后出售,所获利润全部捐给“幸福村 ”.每种文化衫的成本和售价如表 , 假设文化衫全部售出,共获利720元 ,求购进两种文化衫各多少件
白色文化衫 黑色文化衫
成本(元) 25 28
售价(元) 31 36
四、解答题(每小题7分,共28分)
19. 如图 ,在6×6的方格纸中 , 每个小正方形的边长为1,每个小正方形的顶点称为格点 , 请按要求画出格点三角形与格点四边形 .
(1)在图①中以线段AB 为边画一个格点△ABC,使AB=BC;
(2)在图②中以线段AB为边画一个格点四边形 ABCD,使其面积为7, 且 ∠BAD= 90°.
20.如图,在平面直角坐标系中,直线y=-2x+2与x轴、y轴分别相交于点A,B,四边形ABCD是正方形,双曲线 在第一象限经过点D.
(1)求双曲线表示的函数解析式;
(2)将正方形ABCD沿x轴向左平移_____个单位长度时,点C的对应点
恰好落在(1)中的双曲线上.
21.2022年2月4日晚,当我国运动员迪妮格尔·衣拉木江和赵嘉文将最后一棒火炬嵌入主火炬“大雪花”中央时 ,第24届北京冬奥会向世界展示了低碳环保的“点火”仪式 . 小华 有幸在现场目睹这一过程,在“大雪花 ”竖直升起的某一刻 ,从小华的位置(点 O)观测“大雪花”的顶部 A 的仰角α为 12.8°,底部 B 的俯角β为15.3°,已知“大雪花 ”高 AB 约 14.89m ,求小华的位置离“大雪花”的水平距离 OC.(结果精确到0.1m ,参考数据 :tan12.8°≈0.23,sin12.8°≈0.22,tan15.3≈0.27,
sin15.3°≈0.26)
某校组织学生参加“防疫卫生知识竞赛”(满分为100分).竞赛结束后,随机抽取甲、乙两班各40名学生的成绩,并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息。
a.甲、乙两班40名学生数学成绩的频数分布统计表如下:
成绩 班级 50≤x<60 60≤x<70 70≤x<80 80≤x<90 90≤x≤100
甲 4 11 13 10 2
乙 6 3 15 14 2
(说明:成绩80分及以上为优秀,70--79分为良好,60--69分为合格,60分以下为不合格)
b.甲班成绩在70≤x<80这一组的是:70,70,70,71,72,73,73,73,74,75,76,77,78
c.甲、乙两班成绩的平均分、中位数、众数如下:
班级 平均分 中位数 众数
甲 74.2 n 85
乙 73.5 76 84
根据以上信息,回答下列问题:
(1)写出表中n的值,n= ;
(2)在此次测试中,某学生的成绩是74分,在他所属班级排在前20名,由表中数据可知该学生是________(选填“甲”或“乙”)班的学生,理由是_____________________________________________________;
(3)假设学校1200名学生都参加此次竞赛,估计成绩优秀的学生人数.
五、解答题(每小题8分,共16分)
23.甲乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的关系如图,请根据图像所提供的信息解答下列问题
(1)甲队在开挖后6h内,每小时挖_____m
(2)乙队在2≤x≤6时间段内,求y与x之间的函数关系式
(3)直接写出开挖后几个小时时,甲、乙两队挖的河渠的长度相差5m.
24.(1)如图1 ,在Rt△ABC中,∠ABC=90°,以点B为中心,把△ABC逆时针旋转90°,得到△A1BC1;再以点C为中心,把△ABC顺时针旋转90°,得到△A2B1C,连接C1B1,则C1B1与BC的位置关系为__________;
(2)如图2,当△ABC是锐角三角形,∠ABC=α(α≠60°)时,将△ABC按照(1)中的方式旋转α,连接C1B1,探究C1B1与BC的位置关系,写出你的结论,并加以证明;
(3)如图3 ,在图2 的基础上,连接B1B,若C1B1= BC,△C1BB1的面积为4,则△B1BC的面积为_____.
六、解答题(每小题10分,共20分)
25.如图,在 △ABC 中,∠ACB=90°,AC=8,BC=6,点M 为边AB 的中点.点Q 从点 A 出发,沿AC 方向以每秒1个单位长度的速度向终点C 运动,同时点P 从点C 出发, 以每秒2个单位长度的速度先沿CB 方向运动到点B,再沿BA 方向向终点A 运动,以 MP,MQ 为邻边构造 MQEP,设点Q 运动的时间为t秒.
(1)当点E 落在AC 边上时,求t和 MQEP 的面积;
(2)当点P 在边AB上时,设 MQEP 的面积为S(S >0),求S与t之间的函数关系式;
(3)连接CM,直接写出CM 将 MQEP 分成的两部分图形面积相等时t的值.
26.在平面直角坐标系中,二次函数 y=ax2+bx+2 的图象交 x 轴于点 A(﹣3,0)和点 B(1, 0).
(1)此二次函数的图象与 y 轴的交点的纵坐标为_________ .
(2)求此二次函数的关系式.
(3)当﹣2≤x≤3 时,求二次函数 y=ax2+bx+2 的最大值和最小值.
(4)点 P 为二次函数 y=ax2+bx+2(﹣3<x< )图象上任意一点,其横坐标为 m,过点P作PQ//x轴,点 Q 的横坐标为 ﹣2m﹣4.已知点 P 与点 Q 不重合,且线段 PQ 的长度随 m 的增大而减小.直接写出线段 PQ 与二次函数 y=ax2+bx+2(﹣3<x< )的图象只有 1 个公共点时,m 的取值范围.
第 5页(共 6页) 第 6页 (共 6页)
同课章节目录
