2023-2024学年数学七年级第四章一元一次不等式和一元一次不等式组单元测试试题(京改版)(提升卷二)(含解析)
文档属性
| 名称 | 2023-2024学年数学七年级第四章一元一次不等式和一元一次不等式组单元测试试题(京改版)(提升卷二)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 840.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-11 10:03:07 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2023-2024学年数学七年级一元一次不等式和一元一次不等式组(京改版)单元测试 (提升卷二) 含解析
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
评卷人得分
一、单选题(共30分)
1.(本题3分)已知 ,则下列各式中,正确的是( )
A. B.
C. D.
2.(本题3分)下列四个不等式中,一定可以推出的是( )
A. B. C. D.
3.(本题3分)利用数轴确定不等式组的解集,正确的是( )
A. B.
C. D.
4.(本题3分)下列不等式一定成立的是( )
A. B. C. D.
5.(本题3分)若,则下列不等式不一定成立的是( )
A. B. C. D.
6.(本题3分)已知a,b,c是三个非负数,且满足,,设,则s的最小值为( )
A. B. C. D.
7.(本题3分)若关于x的不等式的解集为,则m的值可以取( )
A.0 B.2 C.4 D.6
8.(本题3分)若,则下列结论不一定成立的是( )
A. B.
C. D.
9.(本题3分)已知关于x的不等式组恰有3个整数解,则a的取值范围是( )
A. B. C. D.
10.(本题3分)对非负实数x“四舍五入”到个位的值记为,即当n为非负整数时,若,则.反之,当n为非负整数时,若,则.例如:,.给出下列说法:
①;
②;
③当,m为非负整数时,有;
④若,则非负实数x的取值范围为;
⑤满足的所有非负实数x的值有4个.
以上说法中正确的个数为( )
A.1 B.2 C.3 D.4
评卷人得分
二、填空题(共24分)
11.(本题3分)已知关于x的不等式组有解,实数a的取值范围为 .
12.(本题3分)不等式组的解集是 .
13.(本题3分)若,则 .
14.(本题3分)不等式组的解集为 .
15.(本题3分)关于的不等式组仅有4个整数解,则的取值范围为 .
16.(本题3分)若关于的不等式组无解,则的取值范围是 .
17.(本题3分)已知a、b为常数,且,如果不等式的解集是,那么不等式的解集是 .
18.(本题3分)如图,小明沿街心公园的环形跑道从起点出发按逆时针方向跑步,他用软件记录了跑步的轨迹,他每跑1km软件会在运动轨迹上标注相应的路程,前5km的记录如图所示.已知该环形跑道一圈的周长大于1km.若小明共跑了14km且恰好回到起点,则他共跑了 圈.
评卷人得分
三、解答题(共66分)
19.(本题8分)解不等式组:.
20.(本题8分)解不等式组:.
21.(本题10分)解不等式组,并将其解集表示在数轴上,并写出其所有整数解.
22.(本题10分)“蜂糖李”是安顺的特色农产品,它果大皮薄,味甘甜,深受大家的喜爱.年月日,中华人民共和国农业部批准对“镇宁蜂糖李”实施国家农产品地理标志登记保护,年月日,入选中国农业品牌目录.每年月正是安顺“蜂糖李”上市热销的季节,某水果批发商根据“蜂糖李”的大小购进“大果蜂糖李”和“小果蜂糖李”共箱进行销售,花费元,已知“大果蜂糖李”、“小果蜂糖李”每箱的进价分别为元、元.
(1)求购进“大果蜂糖李”、“小果蜂糖李”两种水果各是多少箱?
(2)现计划用甲、乙两种货车共辆将部分“蜂糖李”运往外地进行销售,它们的运载量如表所示,若运往外地的“蜂糖李”不少于箱,则至多需要乙种货车几辆?
车型 甲种货车 乙种货车
运载量(箱/辆) 60 40
23.(本题10分)某校课后服务开设足球训练营,需要采购一批足球运动装备,市场调查发现每套队服比每个足球多60元,三套队服与五个足球的费用相等
(1)求足球的单价.
(2)该训练营需要购买30套队服和个足球,甲、乙两商家以同样的价格出售所需商品,各自优惠方案不同:
商家 优惠方案
甲 每购买10套队服,送1个足球
乙 购买队服超过20套,则购买足球打8折
①按照以上方案到甲、乙商家购买装备各需费用多少?(用含有y的代数式分别表示).
②请比较到哪个商家购买比较合算?
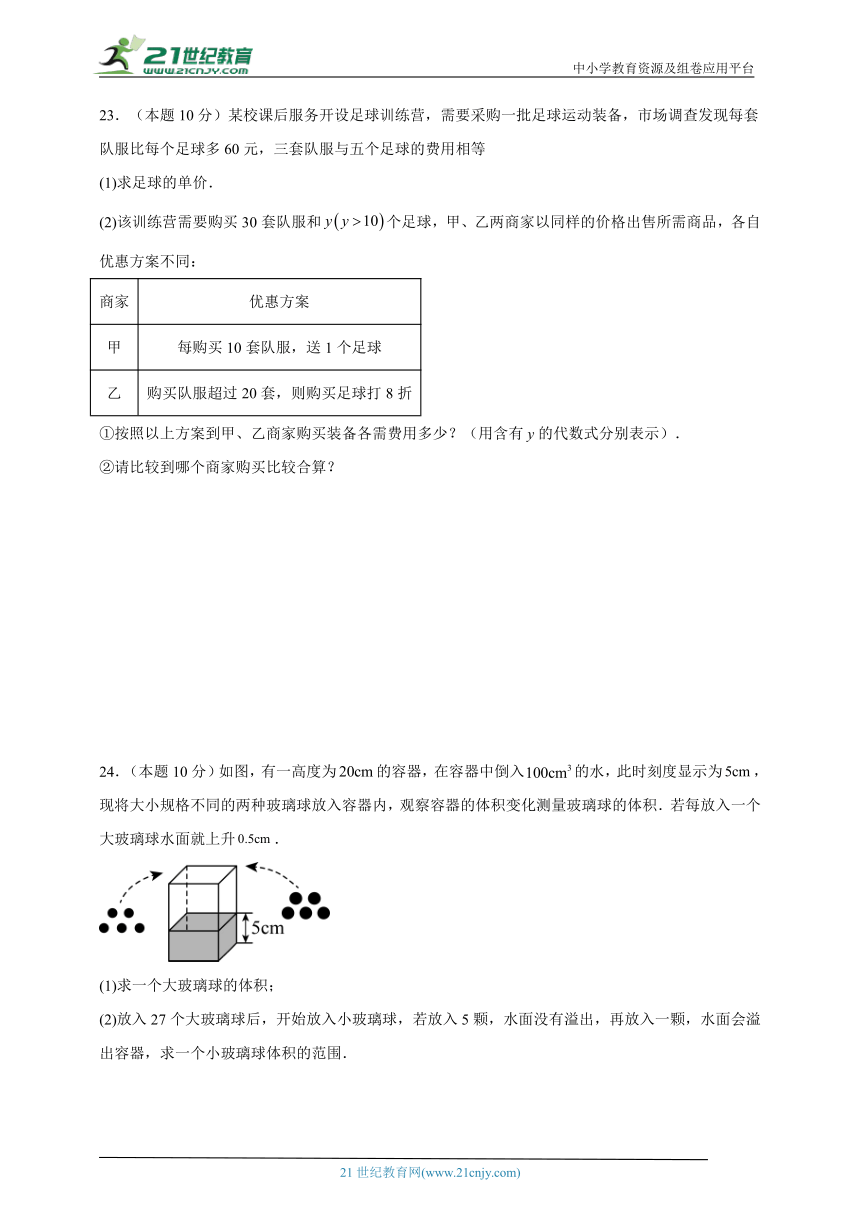
24.(本题10分)如图,有一高度为的容器,在容器中倒入的水,此时刻度显示为,现将大小规格不同的两种玻璃球放入容器内,观察容器的体积变化测量玻璃球的体积.若每放入一个大玻璃球水面就上升.
(1)求一个大玻璃球的体积;
(2)放入27个大玻璃球后,开始放入小玻璃球,若放入5颗,水面没有溢出,再放入一颗,水面会溢出容器,求一个小玻璃球体积的范围.
25.(本题10分)我们知道,表示数轴上数所对应的点与原点的距离,表示数轴上数对应的点与数对应的点之间的距离.请据此解决以下问题:
(1)若方程有解,求的取值范围;
(2)求的最小值;
(3)若不等式有且只有100个整数解,求的取值范围.
参考答案:
1.C
【分析】此题考查了不等式性质的应用能力,关键是能准确理解并运用该知识进行辨别.运用不等式的性质进行逐一辨别、求解.
【详解】解:∵,
∴故A错误;
,故B错误;
,故C正确;
,故D错误
∴选项C符合题意.
故选:C.
2.B
【分析】本题考查不等式的性质.根据不等式的性质逐个判断即可求得答案.
【详解】解:A、若,当时,则,故本选项错误,不符合题意;
B、若,则,故本选项正确,符合题意;
C、若,无法推出,故本选项错误,不符合题意;
D、若,当时,则,故本选项错误,不符合题意;
故选:B
3.D
【分析】此题考查了解一元一次不等式组,以及在数轴上表示不等式的解集,熟练掌握不等式的解法是解本题的关键.分别求出不等式组中两不等式的解集,找出两解集的公共部分即可.
【详解】解:∵
∴
即
∴
故选:D
4.B
【分析】主要考查了不等式的基本性质.(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.根据不等式的基本性质即可作出判断.
【详解】解:A、当时,,故选项错误;
B、正确;
C、当时,,故选项错误;
D、当时,.故选项错误;
故选:B
5.D
【分析】本题考查了不等式的性质,不等式两边加或减同一个数或式子,不等号的方向不变;不等式两边乘或除同一个正数,不等号的方向不变;不等式两边乘或除同一个负数,不等号的方向改变,由此逐项判断即可求解,掌握不等式的性质是解题的关键.
【详解】解:、∵,∴,故该选项成立,不合题意;
、∵,∴,故该选项成立,不合题意;
、∵,∴,∴,故该选项成立,不合题意;
、∵,当时,;
当时,不等式两边除以无意义;
当时,;
故该选项不一定成立,符合题意;
故选:.
6.C
【分析】本题考查了非负数和不等式组的应用能力.先分别用含有c的式子表示出a,b,再根据非负数的定义和列不等式组并求解出c的取值范围,最后将c的最大值代入s进行求解.
【详解】,,
,,
,
,,是三个非负数,
,
解得,
,
解得,
故选:C
7.A
【分析】本题主要考查一元一次不等式的解集与解一元一次不等式,解题的关键是掌握不等式的基本性质3.
根据不等式的基本性质3求解即可.
【详解】解:∵关于x的不等式的解集为,
∴,
则,
∴m可以等于0,不能为2,4,6.
故选:A.
8.D
【分析】本题考查了不等式的性质,根据不等式的性质逐项求解即可,解题的关键是正确理解不等式的两边都加(或减)同一个数,不等号的方向不变,不等式的两边都乘以(或除以)同一个正数,不等号的方向不变;不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.
【详解】、∵,
∴一定成立,此选项符合题意;
、∵,
∴,一定成立,此选项符合题意;
、∵,
∴,一定成立,此选项符合题意;
、当时,得,故原说法不成立,此选项符合题意;
故选:.
9.B
【分析】首先确定不等式组的解集,先利用含a的式子表示,根据题意得到必定有整数解0,再根据恰有3个整数解分类讨论,根据解的情况可以得到关于a的不等式,从而求出a的范围.
【详解】解:
解不等式①得,解不等式②得,
由于不等式组有解,则,必定有整数解0,
∵,
∴三个整数解不可能是.
若三个整数解为,则不等式组无解;
若三个整数解为0,1,2,则;
解得.
故选:B
【点睛】本题考查不等式组的解法及整数解的确定.难度较大,理解题意,根据已知条件得到必定有整数解0,再分类讨论是解题关键.
10.C
【分析】对于①根据新定义直接判断,②可用举反例法判断,③根据题意所述利用不等式的性质判断,④利用对非负实数 “四舍五入”到个位的值记为,进而列出不等式得出的取值范围即可判断,⑤根据新定义得出是的倍数,进而得出的值.
【详解】解:①,故结论正确;
②错误,比如时,,而,故结论②错误;
③为非负整数,则,不影响“四舍五入”,所以当时,故结论③正确;
④∵,
∴,
∴,故④错误;
⑤又∵且为非负实数,即:,
解得:,
若满足,则为整数,必然是的倍数,则,为整数,
则,可得,
即:当,1,2,3时,亦即当,,,时,满足的所有非负实数x的值有4个,故⑤正确;
综上,正确的有①③⑤,共3个;
故选:C.
【点睛】本题考查了四舍五入,解一元一次不等式,以及学生理解题意的能力,关键是看到所得值是个位数四舍五入后的值,问题可得解.
11.
【分析】先求得不等式组的每个不等式的解集,根据不等式组有解,建立起新的不等式组,解之即可,本题考查了一元一次不等式组的解法,能根据不等式组有解建立新不等式组是解题的关键.
【详解】∵,
∴解①得,,解②得,,
∵不等式组有解,
∴,
∴,
故答案为:.
12.
【分析】本题主要考查了解一元一次不等式组,先求出每个不等式的解集,再根据 “同大取大,同小取小,大小小大中间找,大大小小找不到(无解)”求出不等式组的解集即可.
【详解】解:
解不等式①得,
解不等式②得,
∴不等式组的解集为,
故答案为:.
13.
【分析】本题考查不等式的性质,根据不等式的性质,进行判断即可.
【详解】解:两边都乘以,得
,
两边都加,得
,
故答案为:.
14./
【分析】本题考查了解一元一次不等式组,分别求出每个不等式的解集,然后得到不等式组的解集即可.
【详解】解:
解不等式,得,
解不等式,得,
因此不等式组的解集为.
故答案为:.
15.
【分析】本题考查了不等式组的整数解,求不等式组的解集,应遵循以下原则:同大取大,同小取小,小大大小中间找,大大小小解不了.首先解不等式组,即可确定不等式组的整数解,即可确定的范围.
【详解】解:,
由得:,
由得:.
不等式组有四个整数解,
不等式组的整数解是:,0,1,2.
则实数的取值范围是:.
故答案为:.
16.
【分析】本题考查不等式的解集,解题的关键是理解不等式组解集的定义.根据不等式组的解集的定义可知,不等式组中两个不等式的解集没有公共部分,进而得出的取值范围.
【详解】解:关于的不等式组无解,也就是两个不等式解集没有公共部分,
即,没有公共部分,
,
故答案为:.
17.
【分析】本题考查了不等式的解集.不等式的解集是,判断出且,再解出不等式的解集即可.
【详解】解:∵不等式的解集是,
根据不等式的性质可知,当时,不等式的解集为不符合题意,
∴可以判断出,即不等式的解集为,
∴,
∵,
∴即,则.
∴不等式的解集为.
故答案为:.
18.10
【分析】本题考查了不等式的应用,由题意可知,小明恰好跑3圈时,路程比多,但小于,再根据一圈的路程比多,据此可得答案.
【详解】小明恰好跑3圈时,路程超过了,但小于,
所以小明跑9圈时,路程超过但小于,
又因为一圈的路程比多,
所以小明共跑了且恰好回到起点,那么他共跑了10圈.
故答案为:10.
19.
【分析】本题考查的是解一元一次不等式组.分别求出每个不等式的解集,再根据同大取大;同小取小;大小小大中间找;大大小小找不到”的原则取它们的公共部分即可确定不等式组的解集.
【详解】解:,
解①得:,
解②得:,
∴不等式组的解集为:.
20.
【分析】本题考查的是解一元一次不等式组,正确求出每一个不等式的解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.分别求出各不等式的解集,再求出其公共解集.
【详解】解:,
由①得,,
由②得,,
故此不等式组的解集为.
21.不等式组的解集为,整数解为,,,0,1,图见解析
【分析】分别求解不等式的解集,进而可得不等式组的解集,然后求整数解即可.
本题考查了解一元一次不等式组,不等式组的整数解.解题的关键在于正确的运算.
【详解】解:
解不等式①得,,
解不等式②得,,
∴不等式组的解集为,
不等式组的解集在数轴上表示如下:
∴不等式组的整数解为,,,0,1.
22.(1)购进“大果蜂糖李” 箱,购进“小果蜂糖李” 箱
(2)至多需要乙种货车3辆
【分析】本题考查了一元一次不等式及一元一次方程的应用:
(1)设购进“大果蜂糖李”x箱,则购进“小果蜂糖李” 箱,根据等量关系列出方程,解方程即可求解;
(2)设需要乙种货车y辆,则需要甲种货车辆,根据不等关系列出一元一次不等式,解不等式即可求解;
理清题意,根据等量关系列出方程及根据不等关系列出不等式是解题的关键.
【详解】(1)解:设购进“大果蜂糖李”箱,则购进“小果蜂糖李” 箱,
根据题意得:,
解得:,
答:购进“大果蜂糖李” 箱,购进“小果蜂糖李” 箱.
(2)设需要乙种货车y辆,则需要甲种货车辆,
根据题意得:,
解得:,
∴至多需要乙种货车3辆.
23.(1)足球的单价为90元;
(2)①到甲商家购买装备所需费用:元, 到乙商家购买装备所需费用:元;② 当训练营需要购买30套队服和15个足球时,在甲乙两个商家所需费用一样多, 当训练营需要购买30套队服和超过15个足球时,在乙商家购买较合算, 当训练营需要购买30套队服和购买足球超过10个而不足15个时,在甲商家购买较合算.
【分析】本题考查了一元一次方程的应用,一元一次不等式的应用,列代数式的应用,以及最优购物问题,找出题目中的等量关系是解题的关键.
(1)设足球的单价为x元,则队服的单价为元,根据题意“三套队服与五个足球的费用相等”,可得到等量关系,列方程求解即可;
(2)①购买装备所需费用=买队服的费用+买足球的费用,用含有y的代数式表示即可; ②由①中的结论,先求出当甲商家的消费=乙商家的消费时,再分情况比较哪个商家购买较合算.
【详解】(1)解:设足球的单价为x元,则队服的单价为元,
根据题意得, , 解得,
答:足球的单价为90元;
(2)①由(1)得足球的单价为90元,则队服的单价为元,
到甲商家购买装备所需费用:,
到乙商家购买装备所需费用:;
②当甲商家的消费=乙商家的消费时,即,
解得,
∴当训练营需要购买30套队服和15个足球时,在甲乙两个商家所需费用一样多,
当甲商家的消费>乙商家的消费时,即,
解得,
∴当训练营需要购买30套队服和超过15个足球时,在乙商家购买较合算,
当甲商家的消费<乙商家的消费时,即,
解得,
又∵,
∴当训练营需要购买30套队服和购买足球超过10个而不足15个时,在甲商家购买较合算.
24.(1)一个大玻璃球的体积为;
(2)一个小玻璃球体积的大于且不大于.
【分析】本题考查了一元一次不等式组的应用以及有理数的混合运算,根据各数量之间的关系,正确列出一元一次不等式组是解题的关键.
(1)利用容器的底面积倒入水的体积水面的高度,可求出容器的底面积,再利用一个大玻璃球的体积容器的底面积放入一个大玻璃球水面上升的高度,即可求出一个大玻璃球的体积;
(2)设一个小玻璃球的体积是,根据“放入27个大玻璃球后,放入5颗小玻璃球,水面没有溢出,再放入一颗小玻璃球,水面会溢出容器”,可列出关于的一元一次不等式组,解之即可得出结论.
【详解】(1)解:根据题意得:容器的底面积为,
一个大玻璃球的体积为.
答:一个大玻璃球的体积为;
(2)解:设一个小玻璃球的体积是,
根据题意得:,
解得:.
答:一个小玻璃球体积的大于且不大于.
25.(1)
(2)
(3)
【分析】本题考查了绝对值及数轴,解不等式组;
(1)考虑x在数轴上表示的点位于数1表示的点与数3表示的点之间的线段上;x在数轴上表示的点位于数1表示的点左边;x在数轴上表示的点位于数3表示的点的右边;就这三种情况考虑即可;
(2)的最小值为2023,的最小值为2021,的最小值为2019,……,的最小值为1,当x在数轴上1012表示的点与1013表示的点间的线段上时,所求式子的值最小,即可求得最小值;
(3)解不等式,根据解集有100个整数,得到k的不等式组,解不等式组即可.
【详解】(1)解:当x在数轴上表示的点位于数1表示的点与数3表示的点之间的线段(不包括线段两个端点)上时,任一数表示的点到数1表示的点与数3表示的点间距离和均为2,则;
当x在数轴上表示的点位于数1表示的点左边或与1表示的点重合时,则x表示的点到2表示的点不小于1,到3表示的点不小于2,则;
同理,x在数轴上表示的点位于数3表示的点的右边或与3表示的点重合时,;
综上,方程有解,的取值范围为;
(2)解:∵的最小值为2023,此时x位于1表示的点与2024表示的点间的线段上;的最小值为2021,此时x位于2表示的点与2023表示的点间的线段上;的最小值为2019,此时x位于3表示的点与2022表示的点间的线段上;……,的最小值为1,此时x位于1012表示的点与1013表示的点间的线段上;
∴当x在数轴上1012表示的点与1013表示的点间的线段上(包括两个端点)时,的值最小,最小值为;
(3)解:由不等式,得,
解得:,
另一方面,由,得,
由题意,得,
解得:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年数学七年级一元一次不等式和一元一次不等式组(京改版)单元测试 (提升卷二) 含解析
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
评卷人得分
一、单选题(共30分)
1.(本题3分)已知 ,则下列各式中,正确的是( )
A. B.
C. D.
2.(本题3分)下列四个不等式中,一定可以推出的是( )
A. B. C. D.
3.(本题3分)利用数轴确定不等式组的解集,正确的是( )
A. B.
C. D.
4.(本题3分)下列不等式一定成立的是( )
A. B. C. D.
5.(本题3分)若,则下列不等式不一定成立的是( )
A. B. C. D.
6.(本题3分)已知a,b,c是三个非负数,且满足,,设,则s的最小值为( )
A. B. C. D.
7.(本题3分)若关于x的不等式的解集为,则m的值可以取( )
A.0 B.2 C.4 D.6
8.(本题3分)若,则下列结论不一定成立的是( )
A. B.
C. D.
9.(本题3分)已知关于x的不等式组恰有3个整数解,则a的取值范围是( )
A. B. C. D.
10.(本题3分)对非负实数x“四舍五入”到个位的值记为,即当n为非负整数时,若,则.反之,当n为非负整数时,若,则.例如:,.给出下列说法:
①;
②;
③当,m为非负整数时,有;
④若,则非负实数x的取值范围为;
⑤满足的所有非负实数x的值有4个.
以上说法中正确的个数为( )
A.1 B.2 C.3 D.4
评卷人得分
二、填空题(共24分)
11.(本题3分)已知关于x的不等式组有解,实数a的取值范围为 .
12.(本题3分)不等式组的解集是 .
13.(本题3分)若,则 .
14.(本题3分)不等式组的解集为 .
15.(本题3分)关于的不等式组仅有4个整数解,则的取值范围为 .
16.(本题3分)若关于的不等式组无解,则的取值范围是 .
17.(本题3分)已知a、b为常数,且,如果不等式的解集是,那么不等式的解集是 .
18.(本题3分)如图,小明沿街心公园的环形跑道从起点出发按逆时针方向跑步,他用软件记录了跑步的轨迹,他每跑1km软件会在运动轨迹上标注相应的路程,前5km的记录如图所示.已知该环形跑道一圈的周长大于1km.若小明共跑了14km且恰好回到起点,则他共跑了 圈.
评卷人得分
三、解答题(共66分)
19.(本题8分)解不等式组:.
20.(本题8分)解不等式组:.
21.(本题10分)解不等式组,并将其解集表示在数轴上,并写出其所有整数解.
22.(本题10分)“蜂糖李”是安顺的特色农产品,它果大皮薄,味甘甜,深受大家的喜爱.年月日,中华人民共和国农业部批准对“镇宁蜂糖李”实施国家农产品地理标志登记保护,年月日,入选中国农业品牌目录.每年月正是安顺“蜂糖李”上市热销的季节,某水果批发商根据“蜂糖李”的大小购进“大果蜂糖李”和“小果蜂糖李”共箱进行销售,花费元,已知“大果蜂糖李”、“小果蜂糖李”每箱的进价分别为元、元.
(1)求购进“大果蜂糖李”、“小果蜂糖李”两种水果各是多少箱?
(2)现计划用甲、乙两种货车共辆将部分“蜂糖李”运往外地进行销售,它们的运载量如表所示,若运往外地的“蜂糖李”不少于箱,则至多需要乙种货车几辆?
车型 甲种货车 乙种货车
运载量(箱/辆) 60 40
23.(本题10分)某校课后服务开设足球训练营,需要采购一批足球运动装备,市场调查发现每套队服比每个足球多60元,三套队服与五个足球的费用相等
(1)求足球的单价.
(2)该训练营需要购买30套队服和个足球,甲、乙两商家以同样的价格出售所需商品,各自优惠方案不同:
商家 优惠方案
甲 每购买10套队服,送1个足球
乙 购买队服超过20套,则购买足球打8折
①按照以上方案到甲、乙商家购买装备各需费用多少?(用含有y的代数式分别表示).
②请比较到哪个商家购买比较合算?
24.(本题10分)如图,有一高度为的容器,在容器中倒入的水,此时刻度显示为,现将大小规格不同的两种玻璃球放入容器内,观察容器的体积变化测量玻璃球的体积.若每放入一个大玻璃球水面就上升.
(1)求一个大玻璃球的体积;
(2)放入27个大玻璃球后,开始放入小玻璃球,若放入5颗,水面没有溢出,再放入一颗,水面会溢出容器,求一个小玻璃球体积的范围.
25.(本题10分)我们知道,表示数轴上数所对应的点与原点的距离,表示数轴上数对应的点与数对应的点之间的距离.请据此解决以下问题:
(1)若方程有解,求的取值范围;
(2)求的最小值;
(3)若不等式有且只有100个整数解,求的取值范围.
参考答案:
1.C
【分析】此题考查了不等式性质的应用能力,关键是能准确理解并运用该知识进行辨别.运用不等式的性质进行逐一辨别、求解.
【详解】解:∵,
∴故A错误;
,故B错误;
,故C正确;
,故D错误
∴选项C符合题意.
故选:C.
2.B
【分析】本题考查不等式的性质.根据不等式的性质逐个判断即可求得答案.
【详解】解:A、若,当时,则,故本选项错误,不符合题意;
B、若,则,故本选项正确,符合题意;
C、若,无法推出,故本选项错误,不符合题意;
D、若,当时,则,故本选项错误,不符合题意;
故选:B
3.D
【分析】此题考查了解一元一次不等式组,以及在数轴上表示不等式的解集,熟练掌握不等式的解法是解本题的关键.分别求出不等式组中两不等式的解集,找出两解集的公共部分即可.
【详解】解:∵
∴
即
∴
故选:D
4.B
【分析】主要考查了不等式的基本性质.(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.根据不等式的基本性质即可作出判断.
【详解】解:A、当时,,故选项错误;
B、正确;
C、当时,,故选项错误;
D、当时,.故选项错误;
故选:B
5.D
【分析】本题考查了不等式的性质,不等式两边加或减同一个数或式子,不等号的方向不变;不等式两边乘或除同一个正数,不等号的方向不变;不等式两边乘或除同一个负数,不等号的方向改变,由此逐项判断即可求解,掌握不等式的性质是解题的关键.
【详解】解:、∵,∴,故该选项成立,不合题意;
、∵,∴,故该选项成立,不合题意;
、∵,∴,∴,故该选项成立,不合题意;
、∵,当时,;
当时,不等式两边除以无意义;
当时,;
故该选项不一定成立,符合题意;
故选:.
6.C
【分析】本题考查了非负数和不等式组的应用能力.先分别用含有c的式子表示出a,b,再根据非负数的定义和列不等式组并求解出c的取值范围,最后将c的最大值代入s进行求解.
【详解】,,
,,
,
,,是三个非负数,
,
解得,
,
解得,
故选:C
7.A
【分析】本题主要考查一元一次不等式的解集与解一元一次不等式,解题的关键是掌握不等式的基本性质3.
根据不等式的基本性质3求解即可.
【详解】解:∵关于x的不等式的解集为,
∴,
则,
∴m可以等于0,不能为2,4,6.
故选:A.
8.D
【分析】本题考查了不等式的性质,根据不等式的性质逐项求解即可,解题的关键是正确理解不等式的两边都加(或减)同一个数,不等号的方向不变,不等式的两边都乘以(或除以)同一个正数,不等号的方向不变;不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.
【详解】、∵,
∴一定成立,此选项符合题意;
、∵,
∴,一定成立,此选项符合题意;
、∵,
∴,一定成立,此选项符合题意;
、当时,得,故原说法不成立,此选项符合题意;
故选:.
9.B
【分析】首先确定不等式组的解集,先利用含a的式子表示,根据题意得到必定有整数解0,再根据恰有3个整数解分类讨论,根据解的情况可以得到关于a的不等式,从而求出a的范围.
【详解】解:
解不等式①得,解不等式②得,
由于不等式组有解,则,必定有整数解0,
∵,
∴三个整数解不可能是.
若三个整数解为,则不等式组无解;
若三个整数解为0,1,2,则;
解得.
故选:B
【点睛】本题考查不等式组的解法及整数解的确定.难度较大,理解题意,根据已知条件得到必定有整数解0,再分类讨论是解题关键.
10.C
【分析】对于①根据新定义直接判断,②可用举反例法判断,③根据题意所述利用不等式的性质判断,④利用对非负实数 “四舍五入”到个位的值记为,进而列出不等式得出的取值范围即可判断,⑤根据新定义得出是的倍数,进而得出的值.
【详解】解:①,故结论正确;
②错误,比如时,,而,故结论②错误;
③为非负整数,则,不影响“四舍五入”,所以当时,故结论③正确;
④∵,
∴,
∴,故④错误;
⑤又∵且为非负实数,即:,
解得:,
若满足,则为整数,必然是的倍数,则,为整数,
则,可得,
即:当,1,2,3时,亦即当,,,时,满足的所有非负实数x的值有4个,故⑤正确;
综上,正确的有①③⑤,共3个;
故选:C.
【点睛】本题考查了四舍五入,解一元一次不等式,以及学生理解题意的能力,关键是看到所得值是个位数四舍五入后的值,问题可得解.
11.
【分析】先求得不等式组的每个不等式的解集,根据不等式组有解,建立起新的不等式组,解之即可,本题考查了一元一次不等式组的解法,能根据不等式组有解建立新不等式组是解题的关键.
【详解】∵,
∴解①得,,解②得,,
∵不等式组有解,
∴,
∴,
故答案为:.
12.
【分析】本题主要考查了解一元一次不等式组,先求出每个不等式的解集,再根据 “同大取大,同小取小,大小小大中间找,大大小小找不到(无解)”求出不等式组的解集即可.
【详解】解:
解不等式①得,
解不等式②得,
∴不等式组的解集为,
故答案为:.
13.
【分析】本题考查不等式的性质,根据不等式的性质,进行判断即可.
【详解】解:两边都乘以,得
,
两边都加,得
,
故答案为:.
14./
【分析】本题考查了解一元一次不等式组,分别求出每个不等式的解集,然后得到不等式组的解集即可.
【详解】解:
解不等式,得,
解不等式,得,
因此不等式组的解集为.
故答案为:.
15.
【分析】本题考查了不等式组的整数解,求不等式组的解集,应遵循以下原则:同大取大,同小取小,小大大小中间找,大大小小解不了.首先解不等式组,即可确定不等式组的整数解,即可确定的范围.
【详解】解:,
由得:,
由得:.
不等式组有四个整数解,
不等式组的整数解是:,0,1,2.
则实数的取值范围是:.
故答案为:.
16.
【分析】本题考查不等式的解集,解题的关键是理解不等式组解集的定义.根据不等式组的解集的定义可知,不等式组中两个不等式的解集没有公共部分,进而得出的取值范围.
【详解】解:关于的不等式组无解,也就是两个不等式解集没有公共部分,
即,没有公共部分,
,
故答案为:.
17.
【分析】本题考查了不等式的解集.不等式的解集是,判断出且,再解出不等式的解集即可.
【详解】解:∵不等式的解集是,
根据不等式的性质可知,当时,不等式的解集为不符合题意,
∴可以判断出,即不等式的解集为,
∴,
∵,
∴即,则.
∴不等式的解集为.
故答案为:.
18.10
【分析】本题考查了不等式的应用,由题意可知,小明恰好跑3圈时,路程比多,但小于,再根据一圈的路程比多,据此可得答案.
【详解】小明恰好跑3圈时,路程超过了,但小于,
所以小明跑9圈时,路程超过但小于,
又因为一圈的路程比多,
所以小明共跑了且恰好回到起点,那么他共跑了10圈.
故答案为:10.
19.
【分析】本题考查的是解一元一次不等式组.分别求出每个不等式的解集,再根据同大取大;同小取小;大小小大中间找;大大小小找不到”的原则取它们的公共部分即可确定不等式组的解集.
【详解】解:,
解①得:,
解②得:,
∴不等式组的解集为:.
20.
【分析】本题考查的是解一元一次不等式组,正确求出每一个不等式的解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.分别求出各不等式的解集,再求出其公共解集.
【详解】解:,
由①得,,
由②得,,
故此不等式组的解集为.
21.不等式组的解集为,整数解为,,,0,1,图见解析
【分析】分别求解不等式的解集,进而可得不等式组的解集,然后求整数解即可.
本题考查了解一元一次不等式组,不等式组的整数解.解题的关键在于正确的运算.
【详解】解:
解不等式①得,,
解不等式②得,,
∴不等式组的解集为,
不等式组的解集在数轴上表示如下:
∴不等式组的整数解为,,,0,1.
22.(1)购进“大果蜂糖李” 箱,购进“小果蜂糖李” 箱
(2)至多需要乙种货车3辆
【分析】本题考查了一元一次不等式及一元一次方程的应用:
(1)设购进“大果蜂糖李”x箱,则购进“小果蜂糖李” 箱,根据等量关系列出方程,解方程即可求解;
(2)设需要乙种货车y辆,则需要甲种货车辆,根据不等关系列出一元一次不等式,解不等式即可求解;
理清题意,根据等量关系列出方程及根据不等关系列出不等式是解题的关键.
【详解】(1)解:设购进“大果蜂糖李”箱,则购进“小果蜂糖李” 箱,
根据题意得:,
解得:,
答:购进“大果蜂糖李” 箱,购进“小果蜂糖李” 箱.
(2)设需要乙种货车y辆,则需要甲种货车辆,
根据题意得:,
解得:,
∴至多需要乙种货车3辆.
23.(1)足球的单价为90元;
(2)①到甲商家购买装备所需费用:元, 到乙商家购买装备所需费用:元;② 当训练营需要购买30套队服和15个足球时,在甲乙两个商家所需费用一样多, 当训练营需要购买30套队服和超过15个足球时,在乙商家购买较合算, 当训练营需要购买30套队服和购买足球超过10个而不足15个时,在甲商家购买较合算.
【分析】本题考查了一元一次方程的应用,一元一次不等式的应用,列代数式的应用,以及最优购物问题,找出题目中的等量关系是解题的关键.
(1)设足球的单价为x元,则队服的单价为元,根据题意“三套队服与五个足球的费用相等”,可得到等量关系,列方程求解即可;
(2)①购买装备所需费用=买队服的费用+买足球的费用,用含有y的代数式表示即可; ②由①中的结论,先求出当甲商家的消费=乙商家的消费时,再分情况比较哪个商家购买较合算.
【详解】(1)解:设足球的单价为x元,则队服的单价为元,
根据题意得, , 解得,
答:足球的单价为90元;
(2)①由(1)得足球的单价为90元,则队服的单价为元,
到甲商家购买装备所需费用:,
到乙商家购买装备所需费用:;
②当甲商家的消费=乙商家的消费时,即,
解得,
∴当训练营需要购买30套队服和15个足球时,在甲乙两个商家所需费用一样多,
当甲商家的消费>乙商家的消费时,即,
解得,
∴当训练营需要购买30套队服和超过15个足球时,在乙商家购买较合算,
当甲商家的消费<乙商家的消费时,即,
解得,
又∵,
∴当训练营需要购买30套队服和购买足球超过10个而不足15个时,在甲商家购买较合算.
24.(1)一个大玻璃球的体积为;
(2)一个小玻璃球体积的大于且不大于.
【分析】本题考查了一元一次不等式组的应用以及有理数的混合运算,根据各数量之间的关系,正确列出一元一次不等式组是解题的关键.
(1)利用容器的底面积倒入水的体积水面的高度,可求出容器的底面积,再利用一个大玻璃球的体积容器的底面积放入一个大玻璃球水面上升的高度,即可求出一个大玻璃球的体积;
(2)设一个小玻璃球的体积是,根据“放入27个大玻璃球后,放入5颗小玻璃球,水面没有溢出,再放入一颗小玻璃球,水面会溢出容器”,可列出关于的一元一次不等式组,解之即可得出结论.
【详解】(1)解:根据题意得:容器的底面积为,
一个大玻璃球的体积为.
答:一个大玻璃球的体积为;
(2)解:设一个小玻璃球的体积是,
根据题意得:,
解得:.
答:一个小玻璃球体积的大于且不大于.
25.(1)
(2)
(3)
【分析】本题考查了绝对值及数轴,解不等式组;
(1)考虑x在数轴上表示的点位于数1表示的点与数3表示的点之间的线段上;x在数轴上表示的点位于数1表示的点左边;x在数轴上表示的点位于数3表示的点的右边;就这三种情况考虑即可;
(2)的最小值为2023,的最小值为2021,的最小值为2019,……,的最小值为1,当x在数轴上1012表示的点与1013表示的点间的线段上时,所求式子的值最小,即可求得最小值;
(3)解不等式,根据解集有100个整数,得到k的不等式组,解不等式组即可.
【详解】(1)解:当x在数轴上表示的点位于数1表示的点与数3表示的点之间的线段(不包括线段两个端点)上时,任一数表示的点到数1表示的点与数3表示的点间距离和均为2,则;
当x在数轴上表示的点位于数1表示的点左边或与1表示的点重合时,则x表示的点到2表示的点不小于1,到3表示的点不小于2,则;
同理,x在数轴上表示的点位于数3表示的点的右边或与3表示的点重合时,;
综上,方程有解,的取值范围为;
(2)解:∵的最小值为2023,此时x位于1表示的点与2024表示的点间的线段上;的最小值为2021,此时x位于2表示的点与2023表示的点间的线段上;的最小值为2019,此时x位于3表示的点与2022表示的点间的线段上;……,的最小值为1,此时x位于1012表示的点与1013表示的点间的线段上;
∴当x在数轴上1012表示的点与1013表示的点间的线段上(包括两个端点)时,的值最小,最小值为;
(3)解:由不等式,得,
解得:,
另一方面,由,得,
由题意,得,
解得:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第四章 一元一次不等式和一元一次不等式组
- 4.1 不等式
- 4.2 不等式的基本性质
- 4.3 不等式的解集
- 4.4 一元一次不等式及其解法
- 4.5 一元一次不等式组及其解法
- 第五章 二元一次方程组
- 5.1 二元一次方程和它的解
- 5.2 二元一次方程组和它的解
- 5.3 用代入消元法解二元一次方程组
- 5.4 用加减消元法解二元一次方程组
- *5.5 三元一次方程组
- 5.6 二元一次方程组的应用
- 第六章 整式的运算
- 6.1 整式的加减法
- 6.2 幂的运算
- 6.3 整式的乘法
- 6.4 乘法公式
- 6.5 整式的除法
- 第七章 观察、猜想与证明
- 7.1 观察
- 7.2 实验
- 7.3 归纳
- 7.4 类比
- 7.5 猜想
- 7.6 证明
- 7.7 几种简单几何图形及其推理
- 第八章 因式分解
- 8.1 因式分解
- 8.2 提公因式法
- 8.3 公式法
- 第九章 数据的收集与表示
- 9.1 总体与样本
- 9.2 数据的收集与整理
- 9.3 数据的表示——扇形统计图
- 9.4 用计算机绘制统计图
- 9.5 平均数
- 9.6 众数和中位数
