第二章 专题强化4 理想气体的图像问题 液柱移动问题 学案(学生版+教师版)—2024年春高中物理人教版选择性必修三
文档属性
| 名称 | 第二章 专题强化4 理想气体的图像问题 液柱移动问题 学案(学生版+教师版)—2024年春高中物理人教版选择性必修三 |  | |
| 格式 | docx | ||
| 文件大小 | 314.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-03-11 13:58:15 | ||
图片预览


文档简介
专题强化4 理想气体的图像问题 液柱移动问题
[学习目标]
1.会利用图像对气体状态、状态变化及规律进行分析,并应用于解决气体状态变化问题(重点)。
2.学会应用假设法分析液柱(或活塞)的移动问题(难点)。
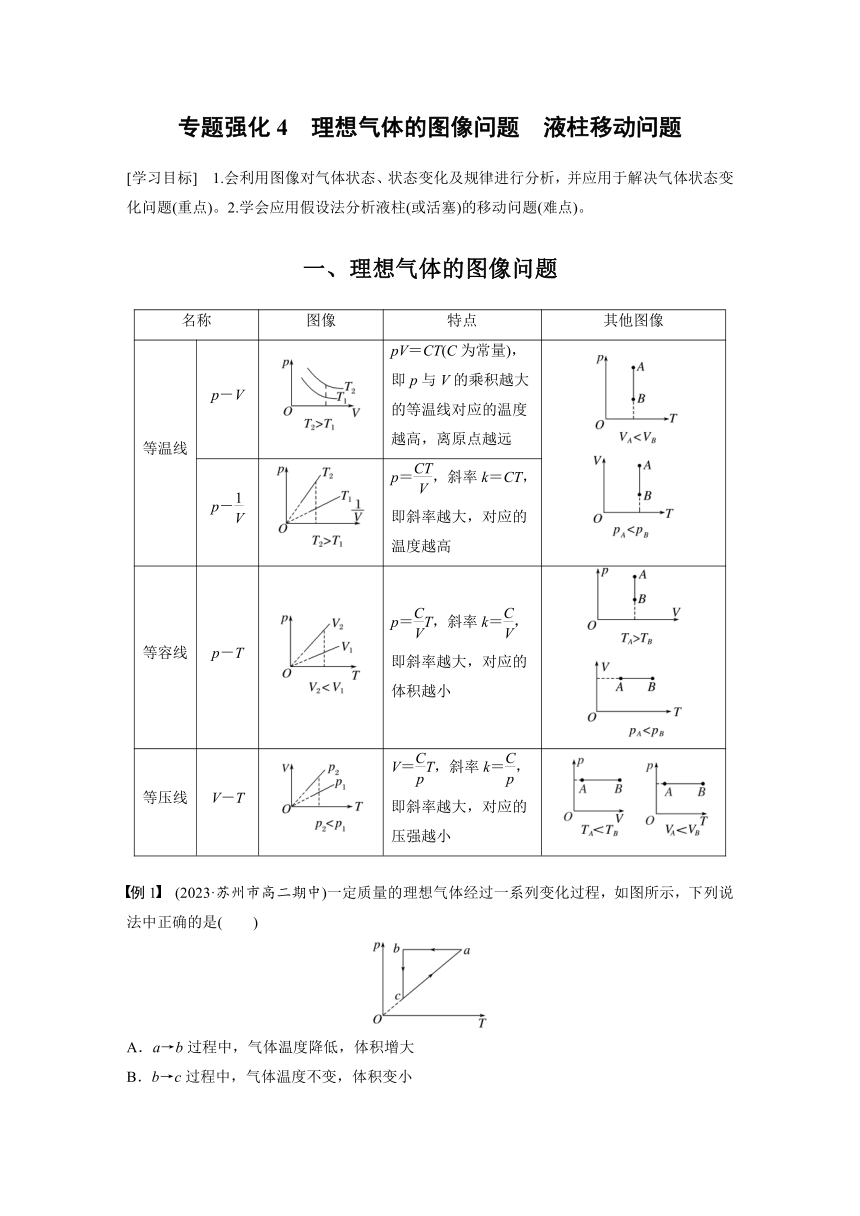
一、理想气体的图像问题
名称 图像 特点 其他图像
等温线 p-V pV=CT(C为常量),即p与V的乘积越大的等温线对应的温度越高,离原点越远
p- p=,斜率k=CT,即斜率越大,对应的温度越高
等容线 p-T p=T,斜率k=,即斜率越大,对应的体积越小
等压线 V-T V=T,斜率k=,即斜率越大,对应的压强越小
例1 (2023·苏州市高二期中)一定质量的理想气体经过一系列变化过程,如图所示,下列说法中正确的是( )
A.a→b过程中,气体温度降低,体积增大
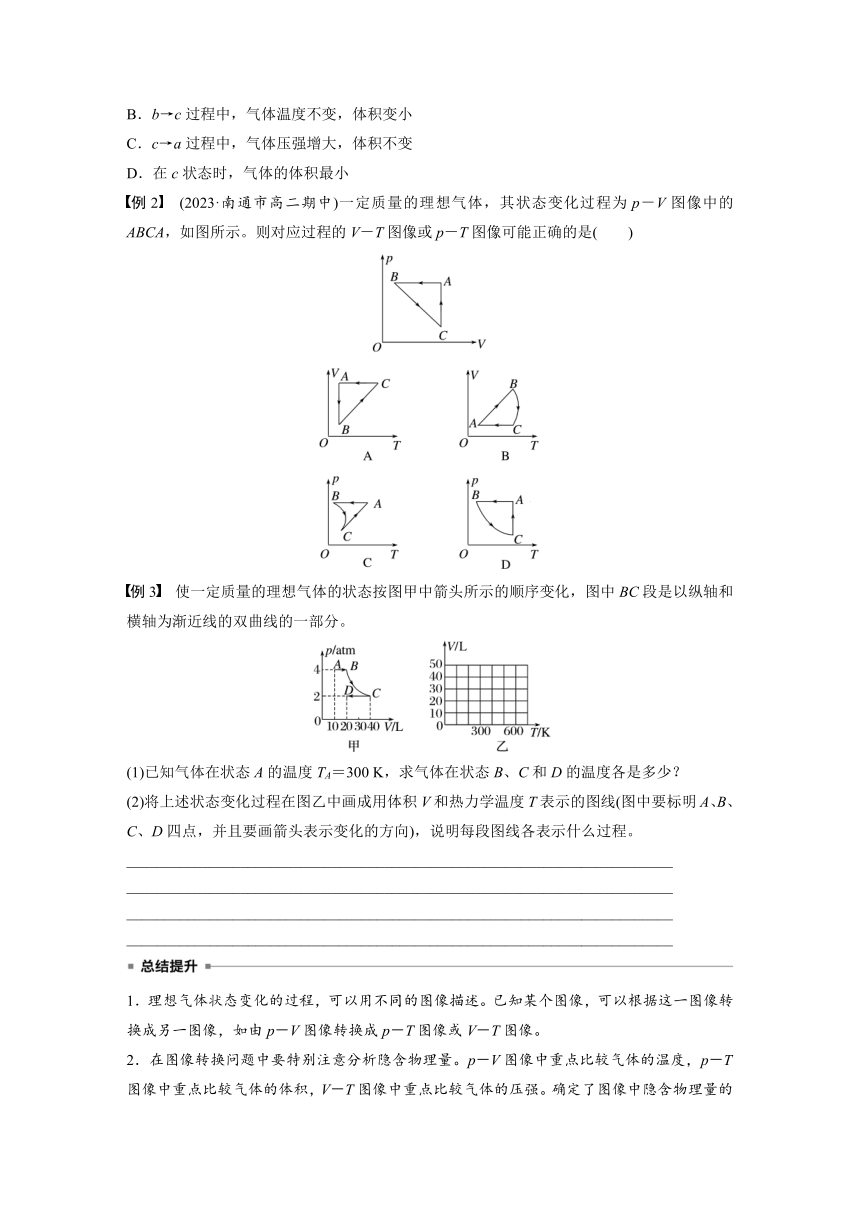
B.b→c过程中,气体温度不变,体积变小
C.c→a过程中,气体压强增大,体积不变
D.在c状态时,气体的体积最小
例2 (2023·南通市高二期中)一定质量的理想气体,其状态变化过程为p-V图像中的ABCA,如图所示。则对应过程的V-T图像或p-T图像可能正确的是( )
例3 使一定质量的理想气体的状态按图甲中箭头所示的顺序变化,图中BC段是以纵轴和横轴为渐近线的双曲线的一部分。
(1)已知气体在状态A的温度TA=300 K,求气体在状态B、C和D的温度各是多少?
(2)将上述状态变化过程在图乙中画成用体积V和热力学温度T表示的图线(图中要标明A、B、C、D四点,并且要画箭头表示变化的方向),说明每段图线各表示什么过程。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
1.理想气体状态变化的过程,可以用不同的图像描述。已知某个图像,可以根据这一图像转换成另一图像,如由p-V图像转换成p-T图像或V-T图像。
2.在图像转换问题中要特别注意分析隐含物理量。p-V图像中重点比较气体的温度,p-T图像中重点比较气体的体积,V-T图像中重点比较气体的压强。确定了图像中隐含物理量的变化,图像转换问题就会迎刃而解。
二、液柱移动问题
分析液柱(或活塞)移动问题常使用假设推理法:根据题设条件,假设液柱不动,运用相应的物理规律及有关知识进行推理。
常用推论有两个:
(1)查理定律的分比形式:=或Δp=p。
(2)盖-吕萨克定律的分比形式:=或ΔV=V。
例4 (2022·宿迁市高二期末)如图所示,A、B两个容器中装有同种气体,容器间用一根细玻璃管连接,管中有一水银滴D作为活塞,当A容器内气体的温度为-10 ℃,B容器内气体的温度为10 ℃时,水银滴刚好在玻璃管的中央保持平衡。两个容器内气体的温度都升高20 ℃时,下列判断正确的是( )
A.水银滴将不移动
B.水银滴将向A移动
C.水银滴将向B移动
D.无法判断水银滴将向哪个方向移动
例5 如图所示,两根粗细相同、两端开口的直玻璃管A和B,竖直插入同一水银槽中,各用一段水银柱封闭着温度相同的空气,空气柱长度H1>H2,水银柱长度h1>h2,现使封闭气柱升高相同的温度(外界大气压保持不变),则两管中气柱上方水银柱的移动情况是( )
A.均向上移动,B中水银柱移动较多
B.均向上移动,A中水银柱移动较多
C.均向下移动,B中水银柱移动较多
D.均向上移动,两管中水银柱移动情况相同
专题强化4 理想气体的图像问题 液柱移动问题
[学习目标] 1.会利用图像对气体状态、状态变化及规律进行分析,并应用于解决气体状态变化问题(重点)。2.学会应用假设法分析液柱(或活塞)的移动问题(难点)。
一、理想气体的图像问题
名称 图像 特点 其他图像
等温线 p-V pV=CT(C为常量),即p与V的乘积越大的等温线对应的温度越高,离原点越远
p- p=,斜率k=CT,即斜率越大,对应的温度越高
等容线 p-T p=T,斜率k=,即斜率越大,对应的体积越小
等压线 V-T V=T,斜率k=,即斜率越大,对应的压强越小
例1 (2023·苏州市高二期中)一定质量的理想气体经过一系列变化过程,如图所示,下列说法中正确的是( )
A.a→b过程中,气体温度降低,体积增大
B.b→c过程中,气体温度不变,体积变小
C.c→a过程中,气体压强增大,体积不变
D.在c状态时,气体的体积最小
答案 C
解析 a→b过程中,气体压强不变,温度降低,根据盖-吕萨克定律=C知,体积减小,故A错误;b→c过程中气体的温度保持不变,压强减小,根据玻意耳定律pV=C知,体积增大,故B错误;c→a过程中,由题图可知,p与T成正比,过坐标原点,则气体发生等容变化,体积不变,而压强增大,综上所述可知在b状态时,气体的体积最小,故C正确,D错误。
例2 (2023·南通市高二期中)一定质量的理想气体,其状态变化过程为p-V图像中的ABCA,如图所示。则对应过程的V-T图像或p-T图像可能正确的是( )
答案 C
解析 根据图像可知A→B,压强不变,即不变,故此时V-T图像为一条过原点的倾斜直线;同时此时体积减小,温度降低,A、B错误;根据图像可知C→A,体积不变,即不变,故此时p-T图像为一条过原点的倾斜直线;同时压强增大,温度升高;由图像可知B→C过程中图线为直线,此时pV乘积可能先增大后减小,根据pV=CT可知此时温度可能先升高后降低,C正确,D错误。
例3 使一定质量的理想气体的状态按图甲中箭头所示的顺序变化,图中BC段是以纵轴和横轴为渐近线的双曲线的一部分。
(1)已知气体在状态A的温度TA=300 K,求气体在状态B、C和D的温度各是多少?
(2)将上述状态变化过程在图乙中画成用体积V和热力学温度T表示的图线(图中要标明A、B、C、D四点,并且要画箭头表示变化的方向),说明每段图线各表示什么过程。
答案 (1)600 K 600 K 300 K (2)见解析
解析 由p-V图像可知,气体在A、B、C、D各状态下压强和体积分别为
pA=4 atm,pB=4 atm,pC=2 atm,pD=2 atm,
VA=10 L,VC=40 L,VD=20 L。
(1)根据理想气体状态方程
==,
可得TC=·TA=×300 K=600 K,
TD=·TA=×300 K=300 K,
由题意知B到C是等温变化,
所以TB=TC=600 K。
(2)因由状态B到状态C为等温变化,
由玻意耳定律有pBVB=pCVC,得
VB== L=20 L。
在V-T图像上状态变化过程的图线由A、B、C、D各状态依次连接(如图),AB是等压膨胀过程,BC是等温膨胀过程,CD是等压压缩过程。
1.理想气体状态变化的过程,可以用不同的图像描述。已知某个图像,可以根据这一图像转换成另一图像,如由p-V图像转换成p-T图像或V-T图像。
2.在图像转换问题中要特别注意分析隐含物理量。p-V图像中重点比较气体的温度,p-T图像中重点比较气体的体积,V-T图像中重点比较气体的压强。确定了图像中隐含物理量的变化,图像转换问题就会迎刃而解。
二、液柱移动问题
分析液柱(或活塞)移动问题常使用假设推理法:根据题设条件,假设液柱不动,运用相应的物理规律及有关知识进行推理。
常用推论有两个:
(1)查理定律的分比形式:=或Δp=p。
(2)盖-吕萨克定律的分比形式:=或ΔV=V。
例4 (2022·宿迁市高二期末)如图所示,A、B两个容器中装有同种气体,容器间用一根细玻璃管连接,管中有一水银滴D作为活塞,当A容器内气体的温度为-10 ℃,B容器内气体的温度为10 ℃时,水银滴刚好在玻璃管的中央保持平衡。两个容器内气体的温度都升高20 ℃时,下列判断正确的是( )
A.水银滴将不移动
B.水银滴将向A移动
C.水银滴将向B移动
D.无法判断水银滴将向哪个方向移动
答案 C
解析 假定两个容器内气体的体积不变,初始状态时A、B中气体温度分别为263 K和283 K,当温度升高ΔT时,容器A内气体的压强由p1增至p1′,则Δp1=p1′-p1
容器B内气体的压强由p2增至p2′,则Δp2=p2′-p2,由查理定律得Δp1=·ΔT,Δp2=·ΔT
因为p2=p1,所以Δp1>Δp2,即水银滴将向B容器移动,故选C。
例5 如图所示,两根粗细相同、两端开口的直玻璃管A和B,竖直插入同一水银槽中,各用一段水银柱封闭着温度相同的空气,空气柱长度H1>H2,水银柱长度h1>h2,现使封闭气柱升高相同的温度(外界大气压保持不变),则两管中气柱上方水银柱的移动情况是( )
A.均向上移动,B中水银柱移动较多
B.均向上移动,A中水银柱移动较多
C.均向下移动,B中水银柱移动较多
D.均向上移动,两管中水银柱移动情况相同
答案 B
解析 管内封闭气柱的压强恒等于外界大气压与水银柱因自身重力而产生的压强之和,因外界大气压不变,则管内气体做等压变化,并由此推知,封闭气柱下端的水银柱高度不变。根据盖-吕萨克定律可知=,整理得ΔV=·V,因A、B管中的封闭气体初始温度相同,温度升高ΔT也相同,且ΔT>0,推导出ΔV>0,即A、B管中的封闭气体体积均增大,又因为H1>H2,A管中气体体积较大,所以ΔVA>ΔVB。即A管中气柱长度增加得多一些,故A、B管中气柱上方的水银柱均向上移动,A中水银柱移动较多,故选B。
[学习目标]
1.会利用图像对气体状态、状态变化及规律进行分析,并应用于解决气体状态变化问题(重点)。
2.学会应用假设法分析液柱(或活塞)的移动问题(难点)。
一、理想气体的图像问题
名称 图像 特点 其他图像
等温线 p-V pV=CT(C为常量),即p与V的乘积越大的等温线对应的温度越高,离原点越远
p- p=,斜率k=CT,即斜率越大,对应的温度越高
等容线 p-T p=T,斜率k=,即斜率越大,对应的体积越小
等压线 V-T V=T,斜率k=,即斜率越大,对应的压强越小
例1 (2023·苏州市高二期中)一定质量的理想气体经过一系列变化过程,如图所示,下列说法中正确的是( )
A.a→b过程中,气体温度降低,体积增大
B.b→c过程中,气体温度不变,体积变小
C.c→a过程中,气体压强增大,体积不变
D.在c状态时,气体的体积最小
例2 (2023·南通市高二期中)一定质量的理想气体,其状态变化过程为p-V图像中的ABCA,如图所示。则对应过程的V-T图像或p-T图像可能正确的是( )
例3 使一定质量的理想气体的状态按图甲中箭头所示的顺序变化,图中BC段是以纵轴和横轴为渐近线的双曲线的一部分。
(1)已知气体在状态A的温度TA=300 K,求气体在状态B、C和D的温度各是多少?
(2)将上述状态变化过程在图乙中画成用体积V和热力学温度T表示的图线(图中要标明A、B、C、D四点,并且要画箭头表示变化的方向),说明每段图线各表示什么过程。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
1.理想气体状态变化的过程,可以用不同的图像描述。已知某个图像,可以根据这一图像转换成另一图像,如由p-V图像转换成p-T图像或V-T图像。
2.在图像转换问题中要特别注意分析隐含物理量。p-V图像中重点比较气体的温度,p-T图像中重点比较气体的体积,V-T图像中重点比较气体的压强。确定了图像中隐含物理量的变化,图像转换问题就会迎刃而解。
二、液柱移动问题
分析液柱(或活塞)移动问题常使用假设推理法:根据题设条件,假设液柱不动,运用相应的物理规律及有关知识进行推理。
常用推论有两个:
(1)查理定律的分比形式:=或Δp=p。
(2)盖-吕萨克定律的分比形式:=或ΔV=V。
例4 (2022·宿迁市高二期末)如图所示,A、B两个容器中装有同种气体,容器间用一根细玻璃管连接,管中有一水银滴D作为活塞,当A容器内气体的温度为-10 ℃,B容器内气体的温度为10 ℃时,水银滴刚好在玻璃管的中央保持平衡。两个容器内气体的温度都升高20 ℃时,下列判断正确的是( )
A.水银滴将不移动
B.水银滴将向A移动
C.水银滴将向B移动
D.无法判断水银滴将向哪个方向移动
例5 如图所示,两根粗细相同、两端开口的直玻璃管A和B,竖直插入同一水银槽中,各用一段水银柱封闭着温度相同的空气,空气柱长度H1>H2,水银柱长度h1>h2,现使封闭气柱升高相同的温度(外界大气压保持不变),则两管中气柱上方水银柱的移动情况是( )
A.均向上移动,B中水银柱移动较多
B.均向上移动,A中水银柱移动较多
C.均向下移动,B中水银柱移动较多
D.均向上移动,两管中水银柱移动情况相同
专题强化4 理想气体的图像问题 液柱移动问题
[学习目标] 1.会利用图像对气体状态、状态变化及规律进行分析,并应用于解决气体状态变化问题(重点)。2.学会应用假设法分析液柱(或活塞)的移动问题(难点)。
一、理想气体的图像问题
名称 图像 特点 其他图像
等温线 p-V pV=CT(C为常量),即p与V的乘积越大的等温线对应的温度越高,离原点越远
p- p=,斜率k=CT,即斜率越大,对应的温度越高
等容线 p-T p=T,斜率k=,即斜率越大,对应的体积越小
等压线 V-T V=T,斜率k=,即斜率越大,对应的压强越小
例1 (2023·苏州市高二期中)一定质量的理想气体经过一系列变化过程,如图所示,下列说法中正确的是( )
A.a→b过程中,气体温度降低,体积增大
B.b→c过程中,气体温度不变,体积变小
C.c→a过程中,气体压强增大,体积不变
D.在c状态时,气体的体积最小
答案 C
解析 a→b过程中,气体压强不变,温度降低,根据盖-吕萨克定律=C知,体积减小,故A错误;b→c过程中气体的温度保持不变,压强减小,根据玻意耳定律pV=C知,体积增大,故B错误;c→a过程中,由题图可知,p与T成正比,过坐标原点,则气体发生等容变化,体积不变,而压强增大,综上所述可知在b状态时,气体的体积最小,故C正确,D错误。
例2 (2023·南通市高二期中)一定质量的理想气体,其状态变化过程为p-V图像中的ABCA,如图所示。则对应过程的V-T图像或p-T图像可能正确的是( )
答案 C
解析 根据图像可知A→B,压强不变,即不变,故此时V-T图像为一条过原点的倾斜直线;同时此时体积减小,温度降低,A、B错误;根据图像可知C→A,体积不变,即不变,故此时p-T图像为一条过原点的倾斜直线;同时压强增大,温度升高;由图像可知B→C过程中图线为直线,此时pV乘积可能先增大后减小,根据pV=CT可知此时温度可能先升高后降低,C正确,D错误。
例3 使一定质量的理想气体的状态按图甲中箭头所示的顺序变化,图中BC段是以纵轴和横轴为渐近线的双曲线的一部分。
(1)已知气体在状态A的温度TA=300 K,求气体在状态B、C和D的温度各是多少?
(2)将上述状态变化过程在图乙中画成用体积V和热力学温度T表示的图线(图中要标明A、B、C、D四点,并且要画箭头表示变化的方向),说明每段图线各表示什么过程。
答案 (1)600 K 600 K 300 K (2)见解析
解析 由p-V图像可知,气体在A、B、C、D各状态下压强和体积分别为
pA=4 atm,pB=4 atm,pC=2 atm,pD=2 atm,
VA=10 L,VC=40 L,VD=20 L。
(1)根据理想气体状态方程
==,
可得TC=·TA=×300 K=600 K,
TD=·TA=×300 K=300 K,
由题意知B到C是等温变化,
所以TB=TC=600 K。
(2)因由状态B到状态C为等温变化,
由玻意耳定律有pBVB=pCVC,得
VB== L=20 L。
在V-T图像上状态变化过程的图线由A、B、C、D各状态依次连接(如图),AB是等压膨胀过程,BC是等温膨胀过程,CD是等压压缩过程。
1.理想气体状态变化的过程,可以用不同的图像描述。已知某个图像,可以根据这一图像转换成另一图像,如由p-V图像转换成p-T图像或V-T图像。
2.在图像转换问题中要特别注意分析隐含物理量。p-V图像中重点比较气体的温度,p-T图像中重点比较气体的体积,V-T图像中重点比较气体的压强。确定了图像中隐含物理量的变化,图像转换问题就会迎刃而解。
二、液柱移动问题
分析液柱(或活塞)移动问题常使用假设推理法:根据题设条件,假设液柱不动,运用相应的物理规律及有关知识进行推理。
常用推论有两个:
(1)查理定律的分比形式:=或Δp=p。
(2)盖-吕萨克定律的分比形式:=或ΔV=V。
例4 (2022·宿迁市高二期末)如图所示,A、B两个容器中装有同种气体,容器间用一根细玻璃管连接,管中有一水银滴D作为活塞,当A容器内气体的温度为-10 ℃,B容器内气体的温度为10 ℃时,水银滴刚好在玻璃管的中央保持平衡。两个容器内气体的温度都升高20 ℃时,下列判断正确的是( )
A.水银滴将不移动
B.水银滴将向A移动
C.水银滴将向B移动
D.无法判断水银滴将向哪个方向移动
答案 C
解析 假定两个容器内气体的体积不变,初始状态时A、B中气体温度分别为263 K和283 K,当温度升高ΔT时,容器A内气体的压强由p1增至p1′,则Δp1=p1′-p1
容器B内气体的压强由p2增至p2′,则Δp2=p2′-p2,由查理定律得Δp1=·ΔT,Δp2=·ΔT
因为p2=p1,所以Δp1>Δp2,即水银滴将向B容器移动,故选C。
例5 如图所示,两根粗细相同、两端开口的直玻璃管A和B,竖直插入同一水银槽中,各用一段水银柱封闭着温度相同的空气,空气柱长度H1>H2,水银柱长度h1>h2,现使封闭气柱升高相同的温度(外界大气压保持不变),则两管中气柱上方水银柱的移动情况是( )
A.均向上移动,B中水银柱移动较多
B.均向上移动,A中水银柱移动较多
C.均向下移动,B中水银柱移动较多
D.均向上移动,两管中水银柱移动情况相同
答案 B
解析 管内封闭气柱的压强恒等于外界大气压与水银柱因自身重力而产生的压强之和,因外界大气压不变,则管内气体做等压变化,并由此推知,封闭气柱下端的水银柱高度不变。根据盖-吕萨克定律可知=,整理得ΔV=·V,因A、B管中的封闭气体初始温度相同,温度升高ΔT也相同,且ΔT>0,推导出ΔV>0,即A、B管中的封闭气体体积均增大,又因为H1>H2,A管中气体体积较大,所以ΔVA>ΔVB。即A管中气柱长度增加得多一些,故A、B管中气柱上方的水银柱均向上移动,A中水银柱移动较多,故选B。
同课章节目录
- 第一章 分子动理论
- 1 分子动理论的基本内容
- 2 实验:用油膜法估测油酸分子的大小
- 3 分子运动速率分布规律
- 4 分子动能和分子势能
- 第二章 气体、固体和液体
- 1 温度和温标
- 2 气体的等温变化
- 3 气体的等压变化和等容变化
- 4 固体
- 5 液体
- 第三章 热力学定律
- 1 功、热和内能的改变
- 2 热力学第一定律
- 3 能量守恒定律
- 4 热力学第二定律
- 第四章 原子结构和波粒二象性
- 1 普朗克黑体辐射理论
- 2 光电效应
- 3 原子的核式结构模型
- 4 氢原子光谱和玻尔的原子模型
- 5 粒子的波动性和量子力学的建立
- 第五章 原子核
- 1 原子核的组成
- 2 放射性元素的衰变
- 3 核力与结合能
- 4 核裂变与核聚变
- 5 “基本”粒子
