新课标人教A版 选修2-2第二章推理与证明复习课
文档属性
| 名称 | 新课标人教A版 选修2-2第二章推理与证明复习课 |  | |
| 格式 | rar | ||
| 文件大小 | 209.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-04-30 21:08:00 | ||
图片预览









文档简介
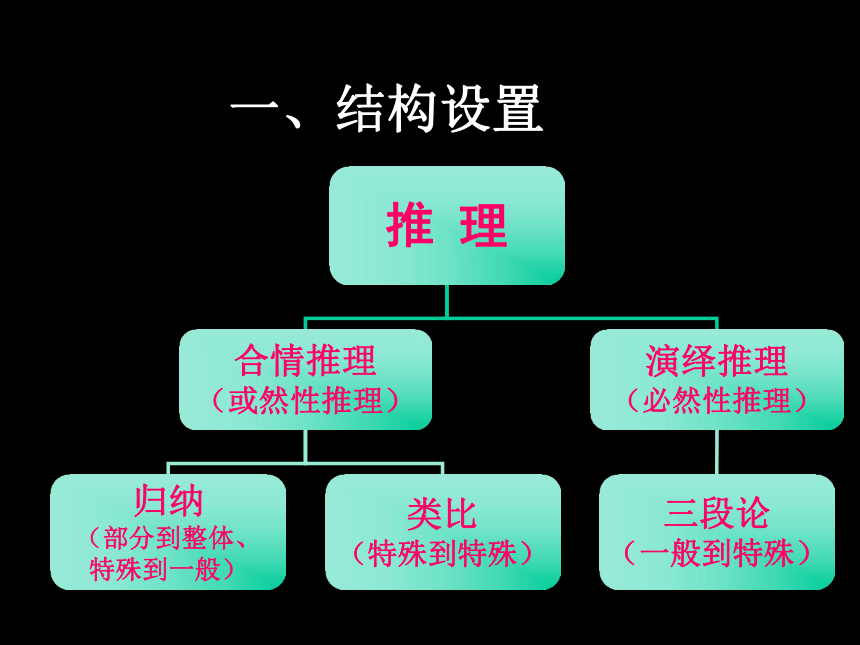
课件30张PPT。第二章推理与证明复习 一、结构设置二、教学目标1.了解合情推理和演绎推理的含义。
2.能正确地运用合情推理和演绎推理进行简单的推理。
3.了解合情推理与演绎推理之间的联系与差别。
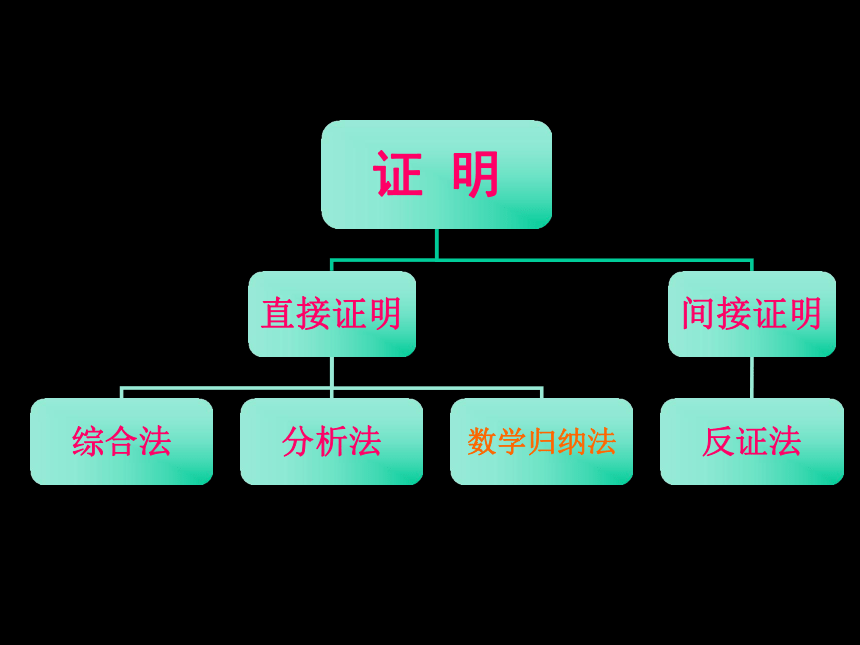
4.了解直接证明的两种基本方法——分析法和综合法的思考过程、特点。
5.了解间接证明的一种基本方法──反证法的思考过程、特点。
6.了解数学归纳法的原理,能用数学归纳法证明一些简单的数学命题。
1.归纳推理的一般步骤:⑴ 对有限的资料进行观察、分析、归纳 整理;
⑵ 提出带有规律性的结论,即猜想;
⑶ 检验猜想。 归纳推理的特点:(1). 归纳推理的前提是几个已知的特殊现象,归纳所得的结论是尚属未知的一般现象,该结论超越了前提所包容的范围。(3). 归纳推理是一种具有创造性的推理.通过归纳推理得到的猜想,可以作为进一步研究的起点,帮助人们发现问题和提出问题。(2). 由归纳推理得到的结论具有猜测的性质,结论是否真实,还需经过逻辑证明和实践检验.因此,它不能作为数学证明的工具。类比推理的一般步骤:⑴ 找出两类对象之间可以确切表述的相似特征;
⑵ 用一类对象的已知特征去推测另一类对象的特征,从而得出一个猜想;
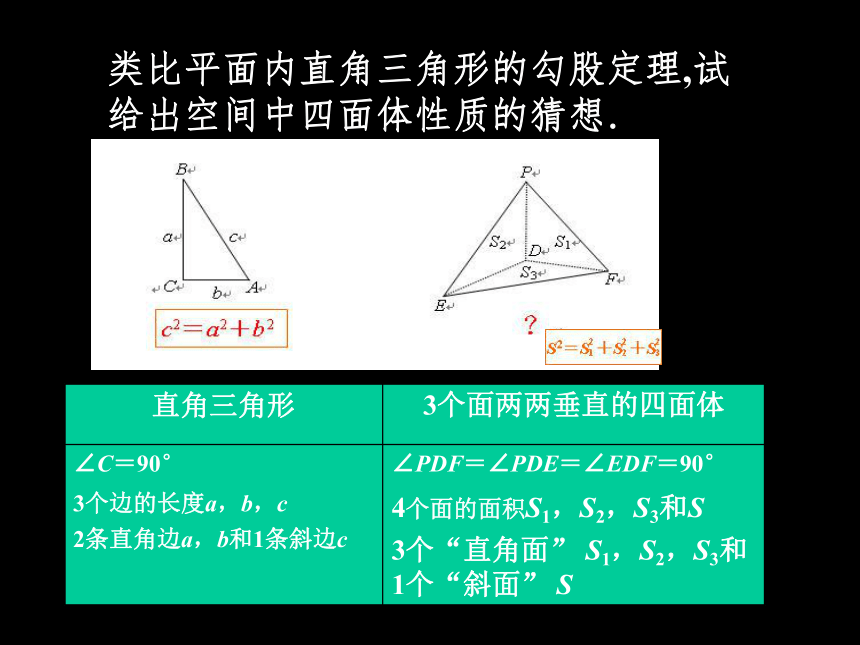
⑶ 检验猜想。 2.在两类不同事物之间进行对比,找出若干相同或相似点之后,推测在其他方面也可以存在相同或相似之处的一种推理模式, 称为类比推理.(简称;类比)类比推理的几个特点;1.类比是从人们已经掌握了的事物的属性,推测正在研究的事物的属性,是以旧有的认识为基础,类比出新的结果.2.类比是从一种事物的特殊属性推测另一种事物的特殊属性.3.类比的结果是猜测性的不一定可靠,单它却有发现的功能. 类比推理举例可以从不同角度确定类比对象:构成几何体的元素数目:四面体 三角形 类比平面内直角三角形的勾股定理,试给出空间中四面体性质的猜想.三段论是演绎推理的一般模式,包括: ☆用集合论的观点看,三段论的依据是:若集合M的所有元素都具有性质P,S是M的一个子集,那么S中所有元素也都具有性质P.M3.从一般性的原理出发,推出某个特殊情况下的结论,这种推理称为演绎推理.证明函数 f(x)=-x2+2x 在(-∞,1]上是增函数. 分析:证明本例所依据的大前提是增函数的定义,即函数y=f(x)满足在给定区间内任取自变量的两个值x1,x2,若x1<x2,则有f(x1)<f(x2).
小前提是f(x)=-x2+2x,x∈(-∞,1]满足增函数的定义,这是证明本例的关键. 纠正典型错误⑴ 合情推理的结论不一定正确
费马猜想:任何形如 (n∈N*)的数都是质数.
反例: ⑵ 演绎推理的形式正确,大前提错误,结论也是错误的 合情推理和演绎推理的区别 与联系推理形式:归纳是由部分到整体、个别到一般的推理,类比是由特殊到特殊的推理;而演绎推理是由一般到特殊的推理。
推理所得的结论:合情推理的结论不一定正确,有待进一步证明;演绎推理在前提和推理形式都正确的前提下,得到的结论一定正确。
合情推理的结论需要演绎推理的验证,而演绎推理的内容一般是通过合情推理获得的。 综合法定义
1.回忆、描述
在数学证明中,我们经常从已知条件和某些学过的定义、定理、公理等出发,通过推理推导出所要的结论.
2.举例、体验特点
分析法定义
1.回忆、描述
在数学证明中,我们还经常从要证的结论出发,反推回去,寻求保证结论成立的条件,直到找到一个明显成立的条件为止.
2.举例、体验特点
3.定义 一般地,从要证明的结论出发,逐步寻求推证过程中,使每一步结论成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、定理、定义、公理等)为止,这种证明的方法叫做分析法.
“两头挤” 把分析法和综合法结合起来使用:根据条件的结构特点去转化结论,得到中间结论Q;根据结论的结构特点去转化条件,得到中间条件P.若由P可以推出Q成立,就可以证明结论成立.
反证法1.反证法的特点:
假设原结论不成立,经过正确的推理,最后得出矛盾,因此说明假设错误,从而证明了原命题成立.
2.应用反证法的情形:
直接证明难找到证明思路(例题)、需分成很多类进行讨论(引例). 数学归纳法1.数学归纳法是一种特殊的证明方法,主要用于证明与正整数有关的数学命题。
特点:通过有限个步骤的推理,证明n取无限多个正整数的情形.
2. 数学归纳法的原理:使“多米诺骨牌”全部倒下的两个条件:
⑴ 第一块骨牌倒下;
⑵ 任意相邻的两块骨牌,前一块倒下一定导 致后一块倒下.
两个条件的作用:
条件⑴:奠基;条件⑵:递推关系
数学归纳法的原理:
⑴(归纳奠基):命题对n=n0成立(n0为使猜想成立的最小的正整数);
⑵(归纳递推):命题若对n=k成立,则对k+1也成立(k≥n0).
第二步学生普遍存在的问题:为什么能在假设下进行证明?
1 一同学在电脑中打出如下若干个圈:
○●○○●○○○●○○○○●○○○○○●…
若将此若干个圈依此规律继续下去,得到一系
列的圈,那么在前120个圈中的●有( )个
(A)12 (B) 13 (C)14 (D)152.观察下列数:1,3,2,6,5,15,14,x,y,z,122,…
中x,y,z的值依次是 ( )
(A)42,41,123; (B) 13,39,123;
(C)24,23,123; (D)28,27,123.CA3、有这样一段演绎推理是这样的“有些有理数是真分数,整数是有理数,则整数是真分数”结论显然是错误的,是因为 ( )
A.大前提错误 B.小前提错误
C.推理形式错误 D.非以上错误 4、在十进制中那么在5进制中2004折合成十进制为 ( )
A.29 B. 254 C. 602 D. 2004CB5.设,n∈N,则
A. B.- C. D.-D6.已知 ,猜想的表达式为 ( ) B.A. C.D.B7.由①正方形的对角线相等;②平行四边形的
对角线相等;③正方形是平行四边形,根据
“三段论”推理出一个结论,则这个结论是( )
(A)正方形的对角线相等
(B) 平行四边形的对角线相等
(C) 正方形是平行四边形
(D) 其它A8.在下列表格中,每格填上一个数字后,使每一行
成等差数列,每一列成等比数列,则a+b+c的值是( )(A) 1 (B) 2 (C) 3 (D) 4A
2.能正确地运用合情推理和演绎推理进行简单的推理。
3.了解合情推理与演绎推理之间的联系与差别。
4.了解直接证明的两种基本方法——分析法和综合法的思考过程、特点。
5.了解间接证明的一种基本方法──反证法的思考过程、特点。
6.了解数学归纳法的原理,能用数学归纳法证明一些简单的数学命题。
1.归纳推理的一般步骤:⑴ 对有限的资料进行观察、分析、归纳 整理;
⑵ 提出带有规律性的结论,即猜想;
⑶ 检验猜想。 归纳推理的特点:(1). 归纳推理的前提是几个已知的特殊现象,归纳所得的结论是尚属未知的一般现象,该结论超越了前提所包容的范围。(3). 归纳推理是一种具有创造性的推理.通过归纳推理得到的猜想,可以作为进一步研究的起点,帮助人们发现问题和提出问题。(2). 由归纳推理得到的结论具有猜测的性质,结论是否真实,还需经过逻辑证明和实践检验.因此,它不能作为数学证明的工具。类比推理的一般步骤:⑴ 找出两类对象之间可以确切表述的相似特征;
⑵ 用一类对象的已知特征去推测另一类对象的特征,从而得出一个猜想;
⑶ 检验猜想。 2.在两类不同事物之间进行对比,找出若干相同或相似点之后,推测在其他方面也可以存在相同或相似之处的一种推理模式, 称为类比推理.(简称;类比)类比推理的几个特点;1.类比是从人们已经掌握了的事物的属性,推测正在研究的事物的属性,是以旧有的认识为基础,类比出新的结果.2.类比是从一种事物的特殊属性推测另一种事物的特殊属性.3.类比的结果是猜测性的不一定可靠,单它却有发现的功能. 类比推理举例可以从不同角度确定类比对象:构成几何体的元素数目:四面体 三角形 类比平面内直角三角形的勾股定理,试给出空间中四面体性质的猜想.三段论是演绎推理的一般模式,包括: ☆用集合论的观点看,三段论的依据是:若集合M的所有元素都具有性质P,S是M的一个子集,那么S中所有元素也都具有性质P.M3.从一般性的原理出发,推出某个特殊情况下的结论,这种推理称为演绎推理.证明函数 f(x)=-x2+2x 在(-∞,1]上是增函数. 分析:证明本例所依据的大前提是增函数的定义,即函数y=f(x)满足在给定区间内任取自变量的两个值x1,x2,若x1<x2,则有f(x1)<f(x2).
小前提是f(x)=-x2+2x,x∈(-∞,1]满足增函数的定义,这是证明本例的关键. 纠正典型错误⑴ 合情推理的结论不一定正确
费马猜想:任何形如 (n∈N*)的数都是质数.
反例: ⑵ 演绎推理的形式正确,大前提错误,结论也是错误的 合情推理和演绎推理的区别 与联系推理形式:归纳是由部分到整体、个别到一般的推理,类比是由特殊到特殊的推理;而演绎推理是由一般到特殊的推理。
推理所得的结论:合情推理的结论不一定正确,有待进一步证明;演绎推理在前提和推理形式都正确的前提下,得到的结论一定正确。
合情推理的结论需要演绎推理的验证,而演绎推理的内容一般是通过合情推理获得的。 综合法定义
1.回忆、描述
在数学证明中,我们经常从已知条件和某些学过的定义、定理、公理等出发,通过推理推导出所要的结论.
2.举例、体验特点
分析法定义
1.回忆、描述
在数学证明中,我们还经常从要证的结论出发,反推回去,寻求保证结论成立的条件,直到找到一个明显成立的条件为止.
2.举例、体验特点
3.定义 一般地,从要证明的结论出发,逐步寻求推证过程中,使每一步结论成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、定理、定义、公理等)为止,这种证明的方法叫做分析法.
“两头挤” 把分析法和综合法结合起来使用:根据条件的结构特点去转化结论,得到中间结论Q;根据结论的结构特点去转化条件,得到中间条件P.若由P可以推出Q成立,就可以证明结论成立.
反证法1.反证法的特点:
假设原结论不成立,经过正确的推理,最后得出矛盾,因此说明假设错误,从而证明了原命题成立.
2.应用反证法的情形:
直接证明难找到证明思路(例题)、需分成很多类进行讨论(引例). 数学归纳法1.数学归纳法是一种特殊的证明方法,主要用于证明与正整数有关的数学命题。
特点:通过有限个步骤的推理,证明n取无限多个正整数的情形.
2. 数学归纳法的原理:使“多米诺骨牌”全部倒下的两个条件:
⑴ 第一块骨牌倒下;
⑵ 任意相邻的两块骨牌,前一块倒下一定导 致后一块倒下.
两个条件的作用:
条件⑴:奠基;条件⑵:递推关系
数学归纳法的原理:
⑴(归纳奠基):命题对n=n0成立(n0为使猜想成立的最小的正整数);
⑵(归纳递推):命题若对n=k成立,则对k+1也成立(k≥n0).
第二步学生普遍存在的问题:为什么能在假设下进行证明?
1 一同学在电脑中打出如下若干个圈:
○●○○●○○○●○○○○●○○○○○●…
若将此若干个圈依此规律继续下去,得到一系
列的圈,那么在前120个圈中的●有( )个
(A)12 (B) 13 (C)14 (D)152.观察下列数:1,3,2,6,5,15,14,x,y,z,122,…
中x,y,z的值依次是 ( )
(A)42,41,123; (B) 13,39,123;
(C)24,23,123; (D)28,27,123.CA3、有这样一段演绎推理是这样的“有些有理数是真分数,整数是有理数,则整数是真分数”结论显然是错误的,是因为 ( )
A.大前提错误 B.小前提错误
C.推理形式错误 D.非以上错误 4、在十进制中那么在5进制中2004折合成十进制为 ( )
A.29 B. 254 C. 602 D. 2004CB5.设,n∈N,则
A. B.- C. D.-D6.已知 ,猜想的表达式为 ( ) B.A. C.D.B7.由①正方形的对角线相等;②平行四边形的
对角线相等;③正方形是平行四边形,根据
“三段论”推理出一个结论,则这个结论是( )
(A)正方形的对角线相等
(B) 平行四边形的对角线相等
(C) 正方形是平行四边形
(D) 其它A8.在下列表格中,每格填上一个数字后,使每一行
成等差数列,每一列成等比数列,则a+b+c的值是( )(A) 1 (B) 2 (C) 3 (D) 4A
