方程的根秘函数的零点

课件16张PPT。方程的根与函数的零点观察：下列三个一元二次方程及其相应的二次函数图象①②③-13yxyx1yx10001234-11与与与 如果方程f(x)=0有实数根，那么方程f(x)=0的实根
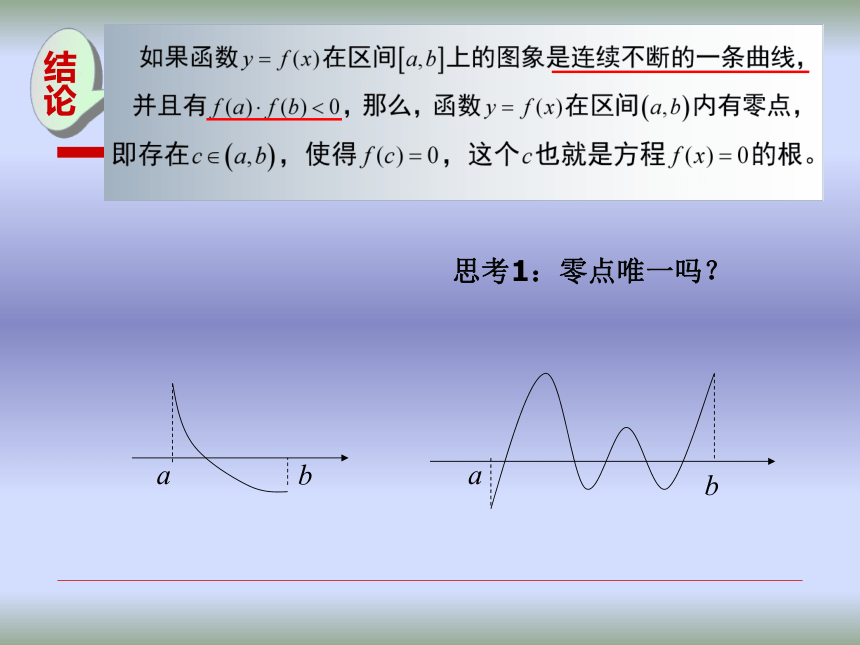
就是函数y=f(x)的图象与x轴的交点的横坐标。推广：方程f(x)=0的根与相应的函数y=f(x)的图象有何关系呢？结论: 零点：012345-1-212345-1-2-3-4xy探究结论思考1：零点唯一吗？结论思考2；若只给条件f(a) · f(b)<0能否保证在(a,b)有零点？思考3：函数y=f(x)在区间[a,b]上的图象是连续不断的一条
曲线：且f(a)·f(b)>0，是否在(a,b)内函数就没有零点？已知函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线：
且 f(a)·f(b)<0 那么 函数y=f(x)在区间(a,b)内有零点；总结：函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线：
（1） f(a)·f(b)<0 函数y=f(x)在区间(a,b)内有零点；学生练习：P88-1(3)提出问题：
怎样寻找函数f(x)=lnx+2x-6的零点的个数？判断：f(x)有一个零点理由：由f(1)=-4<0, f(3)=ln3>0, f(x)在（0，+∞）上连续知f(x)在（0，+∞）存在一个零点c,使得f(c)=0，假设还存在一个不同的零点d，使得f(d)=0，则与f(x)在（0，+∞）上单调递增矛盾，所以f(x)有且只有一个零点。活学活用求下列函数的零点
（1）y=-x2-x+20
(2) y=(x2-2)(x2-3x+2)
若二次函数y=x2+kx-(k-8)与X轴至多有一个交点,求k的取值范围
函数y=| log2|x|-1|有几个零点
练习：小结：等价f(x)=0有实根y=f(x)与x轴有交点y=f(x)有零点等价 如果函数y=f(x)在[a, b]上的图象是连续不断的一条
曲线，并且f(a)·f(b)<0，那么，函数y=f(x)在区间(a, b)内
有零点，即存在c∈(a, b),使得f( c )=0,这个c 就是方程f(x)=0
的根。