3.2列方程解决问题(四)①--复杂相遇1 课件五年级数学下册 沪教版(共20张PPT)
文档属性
| 名称 | 3.2列方程解决问题(四)①--复杂相遇1 课件五年级数学下册 沪教版(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 38.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-12 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
3.2 列方程解决问题(四)①
(复杂相遇问题1)
小学数学·五年级(下)·HJ
能借助线段图分析实际问题中的等量关系,提高用方程解决实际问题的能力。
经历解决问题的过程,体验数学与日常生活密切相关,提高收集信息、处理信息的能力。
学习目标
在实际情境中体会列方程解决问题和算术方法解决问题的不同思路,在比较中进一步感悟方程建模思想,培养数学的应用意识。
掌握列方程解决问题的思考方法和特点。
重点难点
列方程解应用题一般有哪些步骤?
1.用字母表示未知数,并根据题意,用未知数来表示相关的量;
2.找出未知量与已知量之间的等量关系,并列出方程;
3.解方程;
4.检验并写出答句。
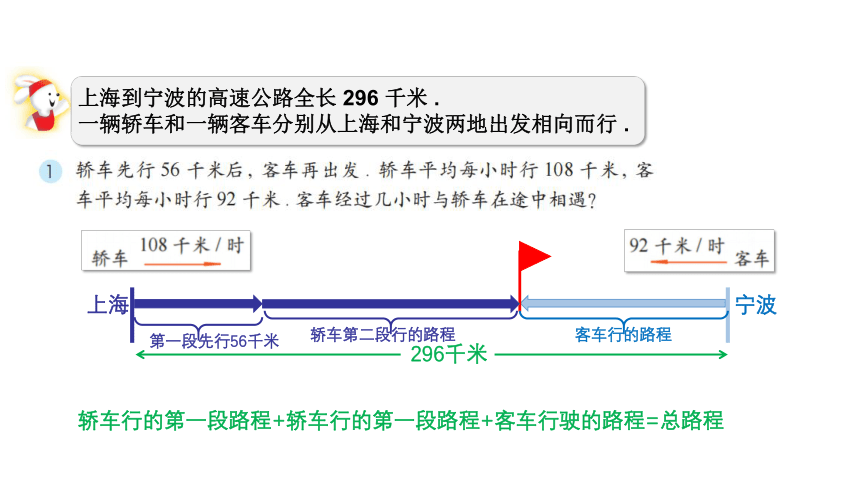
上海到宁波的高速公路全长 296 千米 .
一辆轿车和一辆客车分别从上海和宁波两地出发相向而行 .
上海
宁波
296千米
第一段先行56千米
轿车行的第一段路程+轿车行的第一段路程+客车行驶的路程=总路程
轿车第二段行的路程
客车行的路程
上海到宁波的高速公路全长 296 千米 .
一辆轿车和一辆客车分别从上海和宁波两地出发相向而行 .
轿车行的第一段路程+轿车行的第一段路程+客车行驶的路程=总路程
解:设客车经过x小时与轿车在途中相遇。
56+108x+92x=296
56+200x=296
200x=240
x=1.2
答:客车经过1.2小时与轿车在途中相遇
上海到宁波的高速公路全长 296 千米 .
一辆轿车和一辆客车分别从上海和宁波两地出发相向而行 .
用算术方法解:
剩余路程÷速度和=时间
(296-56)÷(108+92)
=240÷200
=1.2(小时)
答:客车经过1.2小时与轿车在途中相遇。
上海到宁波的高速公路全长 296 千米 .
一辆轿车和一辆客车分别从上海和宁波两地出发相向而行 .
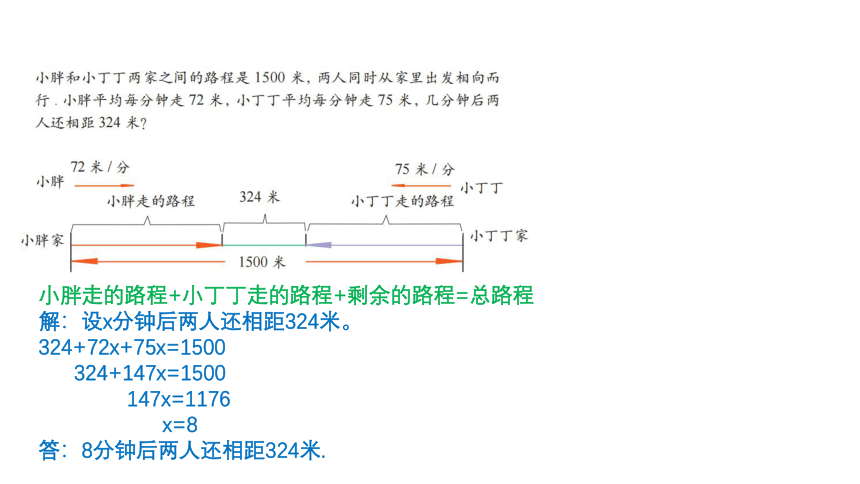
小胖走的路程+小丁丁走的路程+剩余的路程=总路程
解:设x分钟后两人还相距324米。
324+72x+75x=1500
324+147x=1500
147x=1176
x=8
答:8分钟后两人还相距324米.
两人走的路程÷速度和=总路程
(1500-324)÷(72+75)
=1176÷147
=8(分钟)
答:8分钟后两人还相距324米.
课本P35/2
第一队铺的路长+第二队铺的路长+剩余的路长=总路长
解:设第二队平均每天铺柏油x千米。
0.04×20+20x+0.7=2.5
1.5+20x=2.5
20x=1
x=0.05
答:第二队平均每天铺柏油0.05千米。
课本P35/2
两队铺的总路长÷时间-第一队工作效率=第二队工作效率
(2.5-0.7)÷20-0.04
=1.8÷20-0.04
=0.09-0.04
=0.05(千米)
答:第二队平均每天铺柏油0.05千米。
货车行的路程+客车行的路程+剩余的路程=总路程
解:设客车平均每小时行x千米。
62×3+3x+89=500
275+3x=500
3x=225
x=75
答:客车平均每小时行75千米。
两车走的路程÷时间-货车速度=客车速度
(500-89)÷3-62
=411÷3-62
=137-62
=75(千米/小时)
答:客车平均每小时行75千米。
慢车行的路程+快车行的第一段路程+快车行的第二段路程=总路程
解:设慢车开出x小时与快车在途中相遇。
82x+106x+90=1500
188x=1410
x=7.5
答:慢车开出7.5小时与快车在途中相遇。
(总路程-快车先行路程)÷两车速度和=时间
(1500-90)÷(82+106)
=1410÷188
=7.5(小时)
答:慢车开出7.5小时与快车在途中相遇。
练习册P36/B-1
王阿姨先行的路程+王阿姨行的第二段路程+李叔叔行的路程=总路程
解:设李叔叔骑自行车平均每分钟行x千米。
0.07×30+0.07×15+15x=7.95
2.1+1.05+15x=7.95
3.15+15x=7.95
15x=4.8
x=0.32
答:李叔叔骑自行车平均每分钟行0.32千米。
练习册P36/B-1
(总路程-王阿姨先走路程)÷时间-王阿姨速度=李叔叔速度
(7.95-0.07×30)÷15-0.07
=(7.95-2.1)÷15-0.07
=5.85÷15-0.07
=0.39-0.07
=0.32(千米)
答:李叔叔骑自行车平均每分钟行0.32千米。
3.2 列方程解决问题(四)①--复杂相遇1
上海到宁波的高速公路全长 296 千米 .
一辆轿车和一辆客车分别从上海和宁波两地出发相向而行 .
1.课本P30;
2.练习册P35.
3.2 列方程解决问题(四)①
(复杂相遇问题1)
小学数学·五年级(下)·HJ
能借助线段图分析实际问题中的等量关系,提高用方程解决实际问题的能力。
经历解决问题的过程,体验数学与日常生活密切相关,提高收集信息、处理信息的能力。
学习目标
在实际情境中体会列方程解决问题和算术方法解决问题的不同思路,在比较中进一步感悟方程建模思想,培养数学的应用意识。
掌握列方程解决问题的思考方法和特点。
重点难点
列方程解应用题一般有哪些步骤?
1.用字母表示未知数,并根据题意,用未知数来表示相关的量;
2.找出未知量与已知量之间的等量关系,并列出方程;
3.解方程;
4.检验并写出答句。
上海到宁波的高速公路全长 296 千米 .
一辆轿车和一辆客车分别从上海和宁波两地出发相向而行 .
上海
宁波
296千米
第一段先行56千米
轿车行的第一段路程+轿车行的第一段路程+客车行驶的路程=总路程
轿车第二段行的路程
客车行的路程
上海到宁波的高速公路全长 296 千米 .
一辆轿车和一辆客车分别从上海和宁波两地出发相向而行 .
轿车行的第一段路程+轿车行的第一段路程+客车行驶的路程=总路程
解:设客车经过x小时与轿车在途中相遇。
56+108x+92x=296
56+200x=296
200x=240
x=1.2
答:客车经过1.2小时与轿车在途中相遇
上海到宁波的高速公路全长 296 千米 .
一辆轿车和一辆客车分别从上海和宁波两地出发相向而行 .
用算术方法解:
剩余路程÷速度和=时间
(296-56)÷(108+92)
=240÷200
=1.2(小时)
答:客车经过1.2小时与轿车在途中相遇。
上海到宁波的高速公路全长 296 千米 .
一辆轿车和一辆客车分别从上海和宁波两地出发相向而行 .
小胖走的路程+小丁丁走的路程+剩余的路程=总路程
解:设x分钟后两人还相距324米。
324+72x+75x=1500
324+147x=1500
147x=1176
x=8
答:8分钟后两人还相距324米.
两人走的路程÷速度和=总路程
(1500-324)÷(72+75)
=1176÷147
=8(分钟)
答:8分钟后两人还相距324米.
课本P35/2
第一队铺的路长+第二队铺的路长+剩余的路长=总路长
解:设第二队平均每天铺柏油x千米。
0.04×20+20x+0.7=2.5
1.5+20x=2.5
20x=1
x=0.05
答:第二队平均每天铺柏油0.05千米。
课本P35/2
两队铺的总路长÷时间-第一队工作效率=第二队工作效率
(2.5-0.7)÷20-0.04
=1.8÷20-0.04
=0.09-0.04
=0.05(千米)
答:第二队平均每天铺柏油0.05千米。
货车行的路程+客车行的路程+剩余的路程=总路程
解:设客车平均每小时行x千米。
62×3+3x+89=500
275+3x=500
3x=225
x=75
答:客车平均每小时行75千米。
两车走的路程÷时间-货车速度=客车速度
(500-89)÷3-62
=411÷3-62
=137-62
=75(千米/小时)
答:客车平均每小时行75千米。
慢车行的路程+快车行的第一段路程+快车行的第二段路程=总路程
解:设慢车开出x小时与快车在途中相遇。
82x+106x+90=1500
188x=1410
x=7.5
答:慢车开出7.5小时与快车在途中相遇。
(总路程-快车先行路程)÷两车速度和=时间
(1500-90)÷(82+106)
=1410÷188
=7.5(小时)
答:慢车开出7.5小时与快车在途中相遇。
练习册P36/B-1
王阿姨先行的路程+王阿姨行的第二段路程+李叔叔行的路程=总路程
解:设李叔叔骑自行车平均每分钟行x千米。
0.07×30+0.07×15+15x=7.95
2.1+1.05+15x=7.95
3.15+15x=7.95
15x=4.8
x=0.32
答:李叔叔骑自行车平均每分钟行0.32千米。
练习册P36/B-1
(总路程-王阿姨先走路程)÷时间-王阿姨速度=李叔叔速度
(7.95-0.07×30)÷15-0.07
=(7.95-2.1)÷15-0.07
=5.85÷15-0.07
=0.39-0.07
=0.32(千米)
答:李叔叔骑自行车平均每分钟行0.32千米。
3.2 列方程解决问题(四)①--复杂相遇1
上海到宁波的高速公路全长 296 千米 .
一辆轿车和一辆客车分别从上海和宁波两地出发相向而行 .
1.课本P30;
2.练习册P35.
