矩形的性质
图片预览




文档简介
课件14张PPT。特殊的平行四边形
19.2.1 矩形(1)学习目标:1.掌握矩形的概念和性质;理解矩形与平行四边形的区别与联系;
2.会初步运用矩形的概念和性质来解决有关问题。阅读P94-95练习之前并思考下列问题:1.矩形的定义是什么?
2.矩形的有哪些性质?如何证明?如何用符号语言表示?
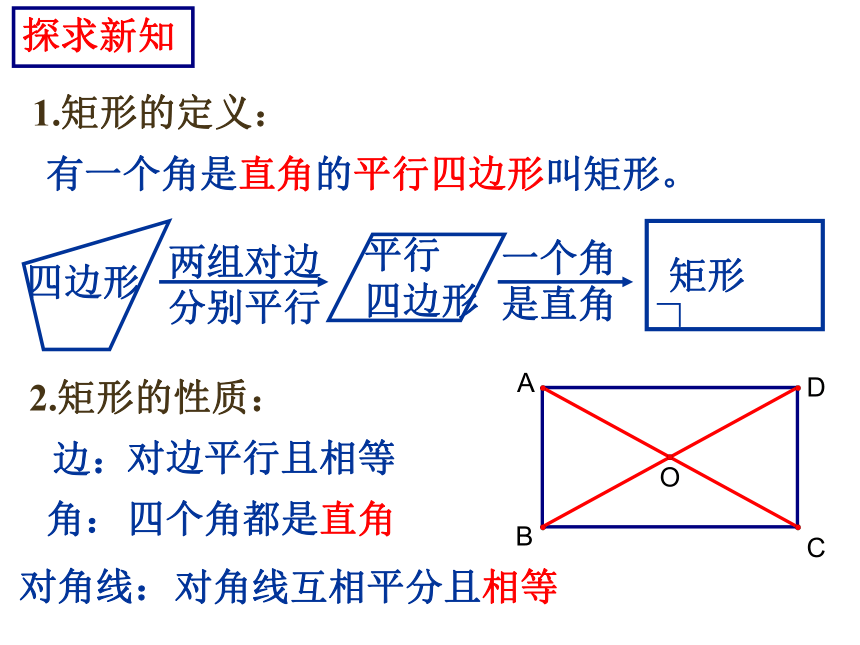
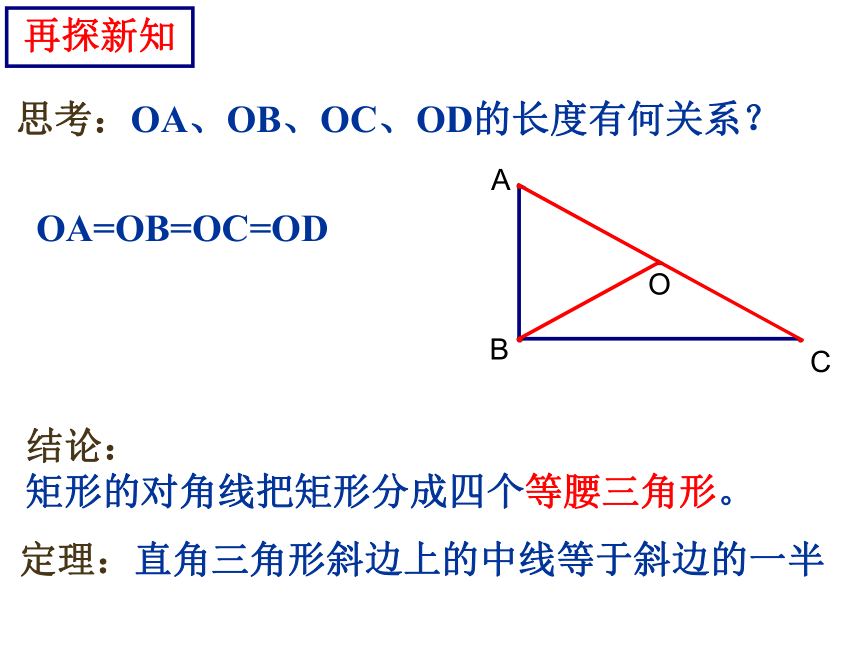
3.矩形是轴对称图形吗?共有几条对称轴?完成P95练习第1,2题;边: 对边平行且相等角:对角相等;邻角互补;内角和360度对角线:对角线互相平分知识回顾平行四边形有哪些性质?探究有一个角是直角的平行四边形叫矩形。2.矩形的性质:对边平行且相等四个角都是直角对角线互相平分且相等1.矩形的定义:边:角:对角线:探求新知思考:OA、OB、OC、OD的长度有何关系?再探新知结论:
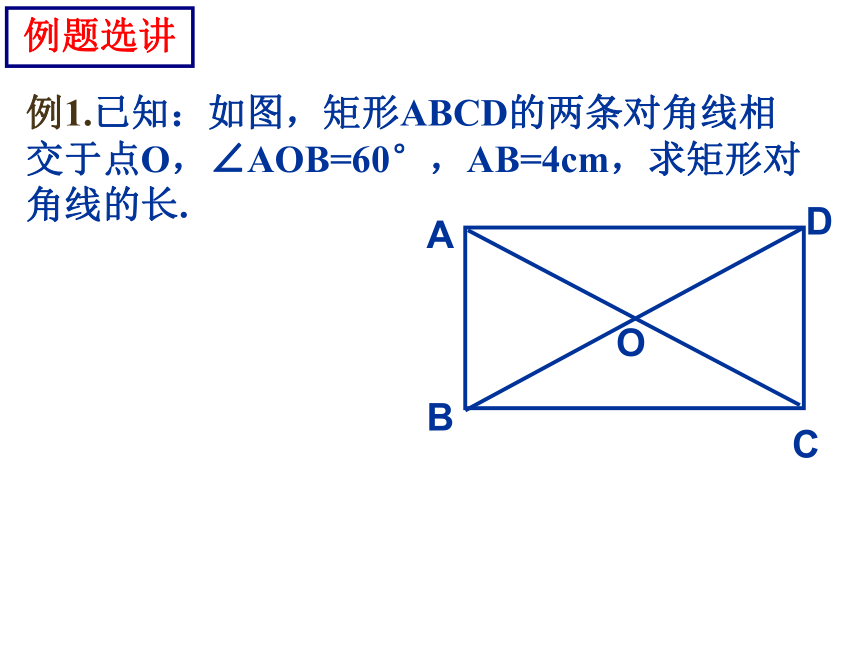
矩形的对角线把矩形分成四个等腰三角形。定理:直角三角形斜边上的中线等于斜边的一半OA=OB=OC=OD例1.已知:如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4cm,求矩形对角线的长.例题选讲随堂练习1. 矩形具有而一般平行四边形不具有的性质是( ).
A 对角线相等 B 对边相等
C 对角相等 D 对角线互相平分 A2.下面性质中,矩形不一定具有的是( )
A对角线相等 B四个角相等
C是轴对称图形 D对角线垂直D随堂练习3.在矩形ABCD中,AE⊥BD
于E,若BE=OE=1,则AC=
___, AB=___424.如图:在矩形ABCD中,两条对角线AC、BD相交于点O, AB=OA,BC=4cm.
求:BD的长和∠ACB的度数。(2).矩形的两条对角线将矩形分成四个面积
相等的等腰三角形( )(1).矩形是轴对称图形( )5.判断题随堂练习 6.如图,若∠BCA=90°,CD⊥AB,AE=BE,∠BCD ︰∠ACD=1︰3,求证:DC=DE拓展应用2.矩形的性质:对边平行且相等四个角都是直角对角线互相平分且相等1.矩形的定义:4.定理:直角三角形斜边上的中线等于斜边的
一半3.结论:矩形的对角线把矩形分成四个面积相等的等腰三角形知识回顾作业11.习题19.2第9题(A本第37次)
2.《感悟》P72(一)基础填空1—5;P73(三)解答题;课外作业1—6 如图, ∠ACB=900,在矩形ABCD中,DE平分∠D交AC于E,交BC于F,若则∠COF=___.随堂训练75°拓展与应用练习如图:在ABCD矩形中AB=6cm,BC=8cm,
将矩形折叠,
使B点与点D重合,
求折痕EF的长。ABOCDA/EF
19.2.1 矩形(1)学习目标:1.掌握矩形的概念和性质;理解矩形与平行四边形的区别与联系;
2.会初步运用矩形的概念和性质来解决有关问题。阅读P94-95练习之前并思考下列问题:1.矩形的定义是什么?
2.矩形的有哪些性质?如何证明?如何用符号语言表示?
3.矩形是轴对称图形吗?共有几条对称轴?完成P95练习第1,2题;边: 对边平行且相等角:对角相等;邻角互补;内角和360度对角线:对角线互相平分知识回顾平行四边形有哪些性质?探究有一个角是直角的平行四边形叫矩形。2.矩形的性质:对边平行且相等四个角都是直角对角线互相平分且相等1.矩形的定义:边:角:对角线:探求新知思考:OA、OB、OC、OD的长度有何关系?再探新知结论:
矩形的对角线把矩形分成四个等腰三角形。定理:直角三角形斜边上的中线等于斜边的一半OA=OB=OC=OD例1.已知:如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4cm,求矩形对角线的长.例题选讲随堂练习1. 矩形具有而一般平行四边形不具有的性质是( ).
A 对角线相等 B 对边相等
C 对角相等 D 对角线互相平分 A2.下面性质中,矩形不一定具有的是( )
A对角线相等 B四个角相等
C是轴对称图形 D对角线垂直D随堂练习3.在矩形ABCD中,AE⊥BD
于E,若BE=OE=1,则AC=
___, AB=___424.如图:在矩形ABCD中,两条对角线AC、BD相交于点O, AB=OA,BC=4cm.
求:BD的长和∠ACB的度数。(2).矩形的两条对角线将矩形分成四个面积
相等的等腰三角形( )(1).矩形是轴对称图形( )5.判断题随堂练习 6.如图,若∠BCA=90°,CD⊥AB,AE=BE,∠BCD ︰∠ACD=1︰3,求证:DC=DE拓展应用2.矩形的性质:对边平行且相等四个角都是直角对角线互相平分且相等1.矩形的定义:4.定理:直角三角形斜边上的中线等于斜边的
一半3.结论:矩形的对角线把矩形分成四个面积相等的等腰三角形知识回顾作业11.习题19.2第9题(A本第37次)
2.《感悟》P72(一)基础填空1—5;P73(三)解答题;课外作业1—6 如图, ∠ACB=900,在矩形ABCD中,DE平分∠D交AC于E,交BC于F,若则∠COF=___.随堂训练75°拓展与应用练习如图:在ABCD矩形中AB=6cm,BC=8cm,
将矩形折叠,
使B点与点D重合,
求折痕EF的长。ABOCDA/EF
